热门标签
热门文章
- 1JQuery 入门 - 附案例代码_jquery前端开发实战教程案例源码(1)_jquery项目实战
- 2Python程序设计之 —— 简易学生信息管理系统_用python做信息管理系统_基于python管理系统
- 3利用Python实现邮件发送_python发邮件
- 4一个悄然崛起的国产开源项目
- 5jquery赋值_jquery发布新版修复严重漏洞，请立即升级！
- 6清华大学刘知远：知识指导的自然语言处理
- 7基于Spring Boot的网上商城购物系统_基于springboot的购物商城
- 8完美解决conda命令出现CondaHTTPError: HTTP 000 CONNECTION FAILED for url报错的终极方法_连不上conda服务器
- 9termux+cpolar+codeserver 自启动 打造远程开发环境_termux vscode server
- 10【通俗易懂区块链】PoS（Proof of Stake）权益证明_通俗易pos
当前位置: article > 正文
程序猿成长之路之密码学篇-AES算法解密详解及代码呈现_aes解密
作者：码创造者 | 2024-07-08 21:42:01
赞
踩
aes解密
各位csdn的小伙伴们大家好呀，我又回来了，这篇文章为上一次介绍AES加密算法的姊妹篇，重点将会详细介绍一下AES算法的解密过程并呈上AES加解密的代码。【暂时不包含iv即偏移量】。下面请跟随我一同进入AES解密的世界。
AES加密详解
如果有小伙伴对AES算法或者AES加密还有所疑问的，可以参考一下我之前写的文章。
https://blog.csdn.net/qq_31236027/article/details/129796471
AES解密
与DES解密仅需要调换密钥组的顺序相比，AES解密会变得更为繁琐。
整体流程
假设大家都了解了AES的加密过程，那么我们知道加密共11轮，而解密亦是如此。加密第一轮就只进行一次轮密钥加，而最后一轮加密则是无需列混淆的参与。解密的过程则恰好相反，解密它先是进行最后一轮加密过程逆置，之后往前递推，直至第一轮加密逆置，如下图所示。
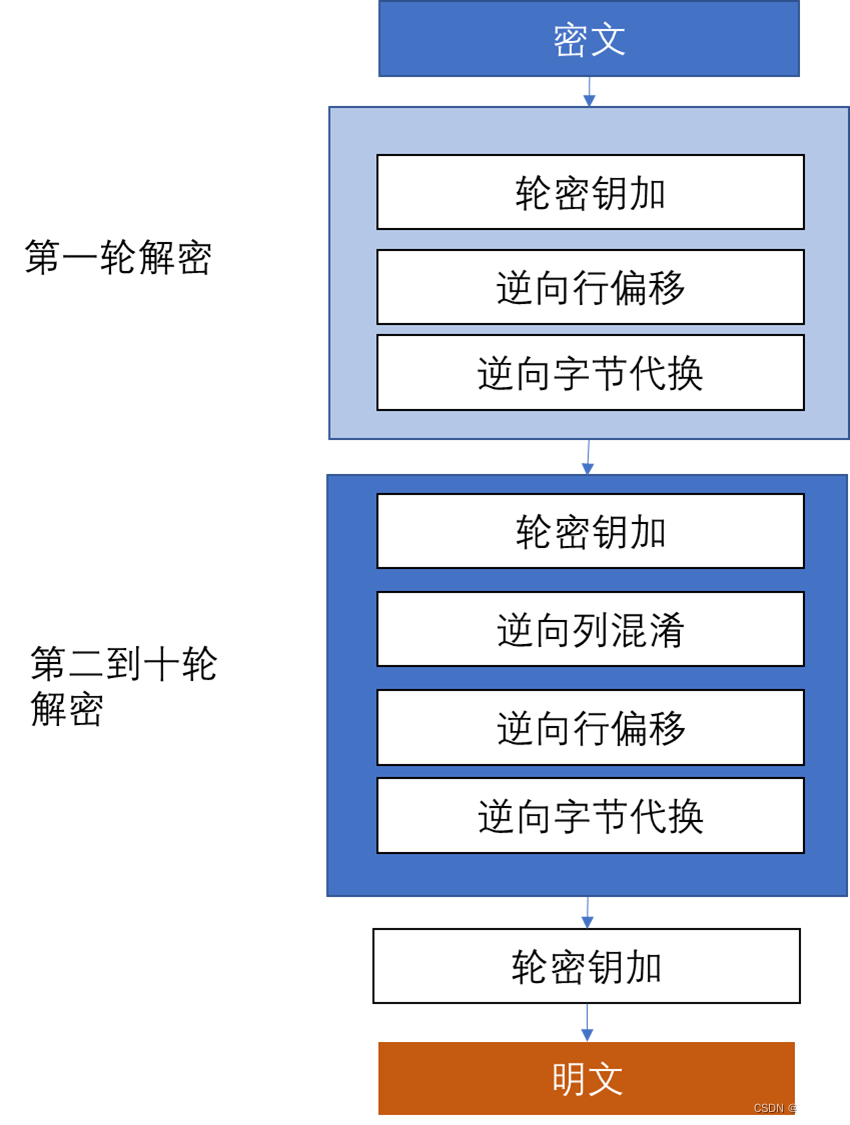
在了解完整体流程后下面就来利用“分而治之”思想，将难点进行拆分讲解。
轮密钥加
密钥参与运算也是从后往前，即加密的最后一轮的密钥参与第一轮的解密。为了方便编程我们可以使用全局变量来存储加解密密钥。这里我不过多介绍密钥的编排原理，大家如有疑问可参考我上一篇介绍AES加密的博客。
逆向行移位
AES加密算法中行移位
第一行不动，第二行循环左移一位，第三行循环左移两位，第四行循环左移三位。
也就是说原来4*4的矩阵中B[0][1] -> B[1][2]（如图中的B1 -> B5) 【注意，此矩阵读法为自上往下，自左往右读】。
为了方便理解和计算，我们可以把这一矩阵一维化成一维数组，即B[0] = B[0][0] = B0, B[1] = B[0][1] = B1, B[2] = B[0][2] = B2 … B[16] = B[3][3] = B15,
那么我们通过数学归纳法，根据移位后B[1] -> B[5], B[2] -> B[10], B[3]->B[15] 易得：B[i] = B[(4 * (i/4) + 5 * (i % 4))mod 16] 【i 为下标】【结合图片更便于理解】
上面是加密中行移位的算法，理解了这一点，解密的逆向行移位就变得简单了。
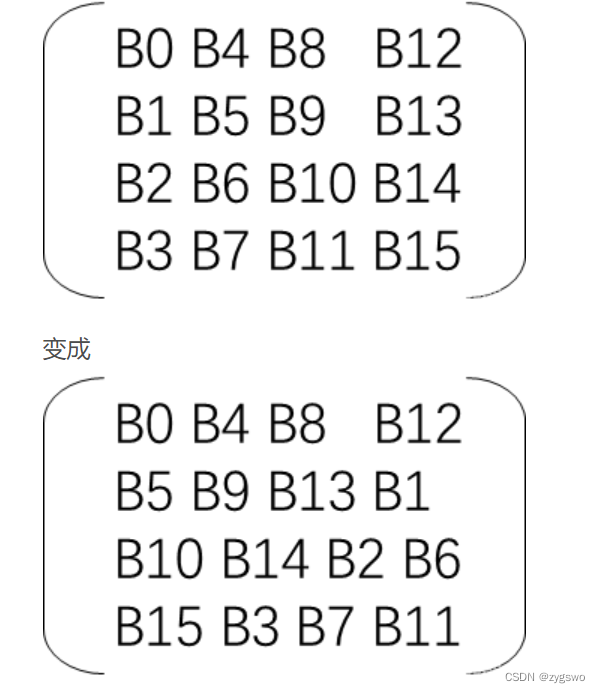
解密无非是将左移改为右移，即 第一行不动，第二行循环右移一位，第三行循环右移两位，第四行循环右移三位。如下图所示
变成
【注意，此矩阵读法为自上往下，自左往右读】。
为了方便理解和计算，我们可以把这一矩阵一维化成一维数组，即B[0] = B[0][0] = B0, B[1] = B[0][1] = B1, B[2] = B[0][2] = B2 … B[16] = B[3][3] = B15,
那么我们同样通过数学归纳法易得：B[i] = B[(4 * (i/4) + 13 * (i % 4))mod 16] 【i 为下标】【结合图片更便于理解】
逆向列混淆
AES加密算法中列混淆
使用伽罗瓦域运算的加法和乘法【伽罗瓦域详见AES介绍文章，运算均为模运算】计算出密文矩阵和列混淆固定矩阵的乘积然后获取结果矩阵。固定矩阵如下图所示：
为了方便计算，也可以将矩阵进行一维化之后进行模数运算。这里我采用了一种比较快速的模数运算方案：
/**
* 算法解释：
* 伽罗瓦域乘法默认为模数运算
* (110)2 * (11)2 => (x^2 + x) * (x + 1) => x^3 + x^2 + x^2 + x => x^3 + x => (1010)2
* 可以理解为先将(110)2左移一位后与(110)进行异或运算 得到 => (1010)2
*/`
while (i < 模数2长度) {
result ^=(numb << (模数2长度 - i)); //表示模数1向左移n位后的值存储于result中并于之前的值进行异或。详见算法解释。
i自加
}
其中numb为模数1的值。之后矩阵模数运算后的结果如果超过8位就要进行归化处理，即与不可约多项式m(x)=x8+x4+x3+x+1（0X11B）进行异或运算
在了解完AES算法的列混淆之后，AES解密的列混淆也就变得简单了，它只要修改固定矩阵就行，如下所示：
{“0E”,“0B”,“0D”,“09”},
{“09”,“0E”,“0B”,“0D”},
{“0D”,“09”,“0E”,“0B”},
{“0B”,“0D”,“09”,“0E”}
逆向字节代换
这个比较简单就是和加密一样，将8位密文前4位作为行数，后4位作为列数在逆置s盒中获值即可。
逆置s盒：
/**
* 逆向s-盒
*/
public static final String[][] REVERSE_SBOX = {
{"52","09","6A","D5","30","36","A5","38","BF","40","A3","9E","81","F3","D7","FB"},
{"7C","E3","39","82","9B","2F","FF","87","34","8E","43","44","C4","DE","E9","CB"},
{"54","7B","94","32","A6","C2","23","3D","EE","4C","95","0B","42","FA","C3","4E"},
{"08","2E","A1","66","28","D9","24","B2","76","5B","A2","49","6D","8B","D1","25"},
{"72","F8","F6","64","86","68","98","16","D4","A4","5C","CC","5D","65","B6","92"},
{"6C","70","48","50","FD","ED","B9","DA","5E","15","46","57","A7","8D","9D","84"},
{"90","D8","AB","00","8C","BC","D3","0A","F7","E4","58","05","B8","B3","45","06"},
{"D0","2C","1E","8F","CA","3F","0F","02","C1","AF","BD","03","01","13","8A","6b"},
{"3A","91","11","41","4F","67","DC","EA","97","F2","CF","CE","F0","B4","E6","73"},
{"96","AC","74","22","E7","AD","35","85","E2","F9","37","E8","1C","75","DF","6E"},
{"47","F1","1A","71","1D","29","C5","89","6F","B7","62","0E","AA","18","BE","1B"},
{"FC","56","3E","4B","C6","D2","79","20","9A","DB","C0","FE","78","CD","5A","F4"},
{"1F","DD","A8","33","88","07","C7","31","B1","12","10","59","27","80","EC","5F"},
{"60","51","7F","A9","19","B5","4A","0D","2D","E5","7A","9F","93","C9","9C","EF"},
{"A0","E0","3B","4D","AE","2A","F5","B0","C8","EB","BB","3C","83","53","99","61"},
{"17","2B","04","7E","BA","77","D6","26","E1","69","14","63","55","21","0C","7d"}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
设计思路
在掌握了解密流程及算法思想后，我们可以进行解密的设计。
- 首先通过一个decrypt方法实现密文分组。
- 通过baseDecrypt方法实现每组的解密。
- 通过decLoop方法实现迭代解密（将轮密钥加、列混淆、行位移、字节代换写在里面）。
- 输出明文。
下面为正式代码：
进制类转换详见文章：
程序猿成长之路之密码学番外篇-----字符串(ascii)转二进制https://blog.csdn.net/qq_31236027/article/details/128579451
package aes;
import java.io.IOException;
import java.nio.charset.Charset;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import common.EncodeUtil;
import common.IEncrytion;
import common.EncodeUtil.EncodeRadix;
import constant.AESConstant;
import sun.misc.BASE64Decoder;
import sun.misc.BASE64Encoder;
/**
* aes 加解密工具(无iv【偏移量】版)
* @author zygswo
*
*/
public class AesUtil implements IEncrytion{
/**
* 密钥对象
*/
private KeyUtil subKeyObj = new KeyUtil().init();
/**
* subkeys
*/
public List<String> subKeys = Collections.synchronizedList(new ArrayList<>());
/**
* 分组加密(128位一组)
* @param text 明文
*/
@Override
public String encrypt(String text) {
StringBuilder sb = new StringBuilder();
int textLen = text.length();
//获取分组长度
// DIV_LEN * CHAR_LEN = 128
// 根据DIV_LEN进行分组，如CHAR_LEN=16位，那么就每8个字符一组
int divLen = textLen % AESConstant.DIV_LEN == 0 ? textLen / AESConstant.DIV_LEN : (textLen / AESConstant.DIV_LEN + 1);
//份组加密处理
for (int i = 0; i < divLen; i++) {
int startIndex = i * AESConstant.DIV_LEN;
int endIndex = (startIndex + AESConstant.DIV_LEN) >= textLen ? textLen : (startIndex + AESConstant.DIV_LEN);
String substr = text.substring(startIndex, endIndex);
//尾部填充
while(substr.length() < AESConstant.DIV_LEN) {
substr += " ";
}
sb.append(baseEncrypt(substr));
}
return new BASE64Encoder().encode(sb.toString().toLowerCase().trim().getBytes());
}
/**
* 加密（每个密文都是128位）
* @param text 需要加密的文本
* @return
*/
private String baseEncrypt(String text) {
//获取11组密钥
if (subKeys == null || subKeys.isEmpty()) {
subKeys = subKeyObj.generateKeys();
}
if (subKeys.size() != 11) {
throw new IllegalArgumentException("密钥长度有误");
}
//转成16进制
return EncodeUtil.binaryToHexStr(
encloops(text, subKeys)
).trim();
}
/**
* 10轮循环加密
* @param step1Result 初始置换后的结果
* @param subKeys 16组子密钥
* @return 循环加密结果
*/
private String encloops(String text, List<String> subKeys) {
//转二进制
String binTempStr = EncodeUtil.strtoBinary(text, AESConstant.CHAR_LEN);
//1.初始化密钥加法层
// System.out.println("binTempStr0 = " + binTempStr);
binTempStr = xor(binTempStr, subKeys.get(0));
//第一轮至第十轮
for(int level = 1; level <= 10; level++) {
// System.out.println("binTempStr1 = " + binTempStr);
//2.字节代换层
String[] temp = replace(binTempStr, AESConstant.SBOX);
//3.扩撒层
//3.1 行位移
temp = shiftRow(temp);
//3.2列混淆
if (level < 10) {
binTempStr = mixColumn(temp);
// System.out.println("binTempStr3 = " + binTempStr);
} else {
binTempStr = "";
for(String str:temp) {
binTempStr += str;
}
}
// System.out.println("binTempStr4 = " + binTempStr);
//4.密钥加法层
binTempStr = xor(binTempStr, subKeys.get(level));
// System.out.println("binTempStr5 = " + binTempStr);
}
// System.out.println("binTempStr6 = " + binTempStr);
return binTempStr;
}
/**
* 列混淆 【重点】
* @param _8bitArr 8位字符串数组 (2进制)
* @return 返回2进制字符串，方便后续的密钥加法
*/
private String mixColumn(String[] _8bitArr) {
StringBuilder sb = new StringBuilder();
for(int i = 0; i < _8bitArr.length; i+=4) {
/**
* 注意：在列混淆中，每一位代表着x的指数，如(2)16=>(10)2 => x, (3)16=>(11)2 => x+1、 (25)16 => (0010 0101)2【采用十六进制】
* 使用矩阵乘积后的结果作为每一字节位上的结果，矩阵相乘用到了异或和或运算，异或模拟GF(2^8)域相乘，或模拟不同位相加
*
* 如
* (01)16*(25)16=> x^5 + x^2 + 1
* (01)16*(25)16=> x^5 + x^2 + 1
* (02)16*(25)16=> x^6 + x^3 + x
* (03)16*(25)16=> x^6 + x^5 + x^3 + x^2 + x + 1
* +____________________________________________
* x^5 + x^2 + 1
*
* 注意如果度》8 要进行模约简
* 模约简方式，与不可约多项式m(x)=x8+x4+x3+x+1（十六进制表示为'11B'）进行相加运算（异或）
*/
for (int j = 0; j < AESConstant.MIX_COLUMN_BOX.length; j++) {
int res = 0;
int rowNb = j;
for (int m = 0; m < AESConstant.MIX_COLUMN_BOX[0].length; m++) {
res ^= Integer.parseInt(
EncodeUtil.binaryToDec(
multiply(_8bitArr[i+j], AESConstant.MIX_COLUMN_BOX[rowNb][m])
)
);
}
//超过了8位就和不可约多项式进行异或
if (res >= 0x100) {
res ^= 0x11B; //11B => 不可约多项式m(x)=x8+x4+x3+x+1
}
//转二进制
String finalRes = EncodeUtil.toBinary(res + "",EncodeRadix.DEC);
//扩充
while(finalRes.length() < 8) {
finalRes = "0" + finalRes;
}
sb.append(finalRes);
}
}
return sb.toString();
}
/**
* 二进制相乘
* @param source - 要处理的数(2进制)
* @param columnBox - 列混淆box(16进制)
* @return 相乘后结果(2进制)
*/
private String multiply(String source, String columnBox) {
//将乘数十六进制转为二进制
String temp = EncodeUtil.toBinary(columnBox, EncodeRadix.HEX);
int result = 0;
for (int i = 0; i < temp.length(); i++) {
//如果开头位为0就跳过
if (temp.charAt(i) == '0') {
continue;
}
//否则就进行计算
//转10进制
int numb = Integer.parseInt(
EncodeUtil.binaryToDec(source)
);
/**
* 算法解释：
* 伽罗瓦域乘法默认为模数运算
* (110)2 * (11)2 => (x^2 + x) * (x + 1) => x^3 + x^2 + x^2 + x => x^3 + x => (1010)2
* 可以理解为先将(110)2左移一位后与(110)进行异或运算 得到 => (1010)2
*/
result ^=(numb << (temp.length()-1-i));
/**
* 注意如果度》8 要进行模约简
* 模约简方式，与不可约多项式m(x)=x8+x4+x3+x+1（十六进制表示为'11B'）进行相加运算（异或）
*/
if (result >= 0x100) {
result ^= 0x11B; //11B => 不可约多项式m(x)=x8+x4+x3+x+1
}
}
return EncodeUtil.toBinary(result+"", EncodeRadix.DEC);
}
/**
* 行位移
* @param _8bitArr 8位字符串数组【16进制】
* @return 按行输出(2进制)
*/
private String[] shiftRow(String[] _8bitArr) {
String[] res = new String[_8bitArr.length];
for(int i = 0; i < _8bitArr.length / 4;i++) {
for (int j = 0; j < 4; j++) {
int index = i*4 + j%4;
//经过行位移后， 原来B0B1B2B3 -> B0B5B10B15, B4B5B6B7 -> B4B9B14B3 。。。 于是找到了这个规律
res[index] = EncodeUtil.toBinary(
_8bitArr[(4*i + 5*j)% _8bitArr.length], EncodeRadix.HEX
);
//扩充
while(res[index].length() < 8) {
res[index]= "0" + res[index];
}
}
}
return res;
}
/**
* 字节代换层
* @param binStr 二进制流
* @param _128bitsStr 128位字符串
* @return 16进制数据
*/
private String[] replace(String _128bitsStr, String[][] sbox) {
String[] result = new String[16];
//分组计算
for (int i = 0; i <result.length; i++) {
String rowNb = EncodeUtil.binaryToDec(_128bitsStr.substring(i * 8, i * 8 + 4));
String colNb = EncodeUtil.binaryToDec(_128bitsStr.substring(i * 8 + 4, i * 8 + 8));
result[i] = sbox[Integer.parseInt(rowNb)][Integer.parseInt(colNb)];
}
return result;
}
/**
* 异或运算
* @param text1 text1
* @param text2 text2
* @return
*/
private String xor(String text1, String text2) {
if (text1 == null || text2 == null || text1.length() != text2.length()) {
throw new IllegalArgumentException("异或运算失败");
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < text1.length();i++) {
char ch1 = text1.charAt(i);
char ch2 = text2.charAt(i);
sb.append((ch1) ^ (ch2));
}
return sb.toString().trim();
}
/**
* 分组解密
* @param encrytedText 密文
*/
@Override
public String decrypt(String encrytedText) {
try {
//base64解码
byte[] bytes = new BASE64Decoder().decodeBuffer(encrytedText);
String str = new String(bytes,Charset.forName("UTF8"));
int textLen = str.length();
StringBuilder sb = new StringBuilder();
int divLen = textLen < 32 ? 1 : (int)(Math.ceil(textLen/(4*8*1.0))); //因为加密后会自动填充所以长度必为字符长度的倍数(HEX 4位)
//分组解密
for (int i = 0; i< divLen; i++) {
int startIndex = i * (4*8);
int endIndex = (startIndex + (4*8));
String temp = str.substring(startIndex, endIndex);
sb.append(baseDecrypt(temp));
}
return sb.toString();
} catch (IOException e) {
e.printStackTrace();
}
return null;
}
/**
* 解密
* @param encHexStr 加密16进制文本
* @return
*/
private String baseDecrypt(String encHexStr) {
//1. 获取密钥
if (subKeys == null || subKeys.isEmpty()) {
throw new IllegalArgumentException("密钥获取失败");
}
if (subKeys.size() != 11) {
throw new IllegalArgumentException("密钥长度有误");
}
//2. 讲16进制转二进制并迭代解密输出结果
return EncodeUtil.binaryToStr(
decLoop(encHexStr,subKeys),
AESConstant.CHAR_LEN
);
}
/**
* 迭代递归解密
* @param encHexStr 加密16进制文本
* @param subKeys 子密钥
* @return 解密结果
*/
private String decLoop(String encHexStr, List<String> subKeys) {
//1.16进制转二进制
String binTempStr = EncodeUtil.toBinary(
encHexStr, EncodeRadix.HEX);
//2.逆向迭代解密
for (int level=10;level > 0;level--) {
//密钥加法层
// System.out.println("reverseReplace binTempStr1 = " + binTempStr);
binTempStr = xor(binTempStr, subKeys.get(level)); //没问题
// System.out.println("reverseReplace binTempStr2 = " + binTempStr);
String[] temp = new String[AESConstant.ARR_LEN];
//转成字符串数组
int len = 8; //字节数组
for (int i = 0; i < AESConstant.ARR_LEN; i++) {
temp[i] = binTempStr.substring(i* len, (i+1)*len);
}
//逆向列混淆层
if (level < 10) {
binTempStr = reverseMixColumn(temp);
// System.out.println("reverseReplace binTempStr3 = " + binTempStr);
for (int i = 0; i < AESConstant.ARR_LEN; i++) {
temp[i] = binTempStr.substring(i* len, (i+1)*len);
}
}
//逆向行位移层
binTempStr = reverseShiftRow(temp);
// System.out.println("reverseReplace binTempStr4 = " + binTempStr);
//逆向字节代换
binTempStr = reverseReplace(binTempStr, AESConstant.REVERSE_SBOX);
// System.out.println("reverseReplace binTempStr5 = " + binTempStr);
}
//密钥加法层
// System.out.println("reverseReplace binTempStr6 = " + binTempStr);
binTempStr = xor(binTempStr, subKeys.get(0));
// System.out.println("reverseReplace binTempStr7 = " + binTempStr);
return binTempStr;
}
/**
* 逆向字节代换层
* @param binStr 二进制流
* @param _128bitsStr 128位字符串
* @return 2进制进制数据
*/
private String reverseReplace(String _128bitsStr, String[][] sbox) {
StringBuilder result = new StringBuilder();
//分组计算
for (int i = 0; i < AESConstant.ARR_LEN; i++) {
String rowNb = EncodeUtil.binaryToDec(_128bitsStr.substring(i * 8, i * 8 + 4));
String colNb = EncodeUtil.binaryToDec(_128bitsStr.substring(i * 8 + 4, i * 8 + 8));
result.append(EncodeUtil.toBinary(sbox[Integer.parseInt(rowNb)][Integer.parseInt(colNb)], EncodeRadix.HEX));
}
return result.toString();
}
/**
* 逆向行位移
* @param _8bitArr 字符串数组(16位)【2进制】
* @return 按行输出(2进制)
*/
private String reverseShiftRow(String[] _8bitArr) {
StringBuilder res = new StringBuilder();
for(int i = 0; i < _8bitArr.length / 4;i++) {
for (int j = 0; j < 4; j++) {
//经过逆向行位移后， 原来B0B1B2B3 -> B0B13B10B7, B4B5B6B7 -> B4B1B14B11 。。。 于是找到了这个规律
String temp =_8bitArr[(4*i + 13*j)% _8bitArr.length];
//扩充
while(temp.length() < 8) {
temp = "0" + temp;
}
res.append(temp);
}
}
return res.toString();
}
/**
* 列混淆 【重点】
* @param _8bitArr 8位字符串数组 (2进制)
* @return 返回2进制字符串，方便后续的密钥加法
*/
private String reverseMixColumn(String[] _8bitArr) {
StringBuilder sb = new StringBuilder();
for(int i = 0; i < _8bitArr.length; i+=4) {
/**
* 注意：在列混淆中，每一位代表着x的指数，如(2)16=>(10)2 => x, (3)16=>(11)2 => x+1、 (25)16 => (0010 0101)2【采用十六进制】
* 使用矩阵乘积后的结果作为每一字节位上的结果，矩阵相乘用到了异或和或运算，异或模拟GF(2^8)域相乘，或模拟不同位相加
*
* 如
* (01)16*(25)16=> x^5 + x^2 + 1
* (01)16*(25)16=> x^5 + x^2 + 1
* (02)16*(25)16=> x^6 + x^3 + x
* (03)16*(25)16=> x^6 + x^5 + x^3 + x^2 + x + 1
* +____________________________________________
* x^5 + x^2 + 1
*
* 注意如果度》8 要进行模约简
* 模约简方式，与不可约多项式m(x)=x8+x4+x3+x+1（十六进制表示为'11B'）进行相加运算（异或）
*/
for (int j = 0; j < AESConstant.REVERSE_MIX_COLUMN_BOX.length; j++) {
int res = 0;
int rowNb = j;
int initLen = _8bitArr[i+j].length();
for (int m = 0; m < AESConstant.REVERSE_MIX_COLUMN_BOX[0].length; m++) {
res ^= Integer.parseInt(
EncodeUtil.binaryToDec(
multiply(_8bitArr[i+j], AESConstant.REVERSE_MIX_COLUMN_BOX[rowNb][m])
)
);
}
//超过了8位就和不可约多项式进行异或
if (res >= 0x100) {
res ^= 0x11B; //11B => 不可约多项式m(x)=x8+x4+x3+x+1
}
//转二进制
String finalRes = EncodeUtil.toBinary(res + "",EncodeRadix.DEC);
//扩充
while(finalRes.length() < initLen) {
finalRes = "0" + finalRes;
}
sb.append(finalRes);
}
}
return sb.toString();
}
public static void main(String[] args) {
AesUtil util = new AesUtil();
String encrytedStr = util.encrypt("{\"code\":200,\"message\":\"成功！\",\"data\":{\"id\":\"2103813902831\",\"name\":\"章鱼哥是我哦\"}}");
System.out.println("encrytedStr = " + encrytedStr);
System.out.println("result= " + util.decrypt(encrytedStr));
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 333
- 334
- 335
- 336
- 337
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
- 350
- 351
- 352
- 353
- 354
- 355
- 356
- 357
- 358
- 359
- 360
- 361
- 362
- 363
- 364
- 365
- 366
- 367
- 368
- 369
- 370
- 371
- 372
- 373
- 374
- 375
- 376
- 377
- 378
- 379
- 380
- 381
- 382
- 383
- 384
- 385
- 386
- 387
- 388
- 389
- 390
- 391
- 392
- 393
- 394
- 395
- 396
- 397
- 398
- 399
- 400
- 401
- 402
- 403
- 404
- 405
- 406
- 407
- 408
- 409
- 410
- 411
- 412
- 413
- 414
- 415
- 416
- 417
- 418
- 419
- 420
- 421
- 422
- 423
- 424
- 425
- 426
- 427
- 428
- 429
- 430
- 431
- 432
- 433
- 434
- 435
- 436
- 437
- 438
- 439
- 440
- 441
- 442
- 443
- 444
- 445
- 446
- 447
- 448
- 449
运行结果
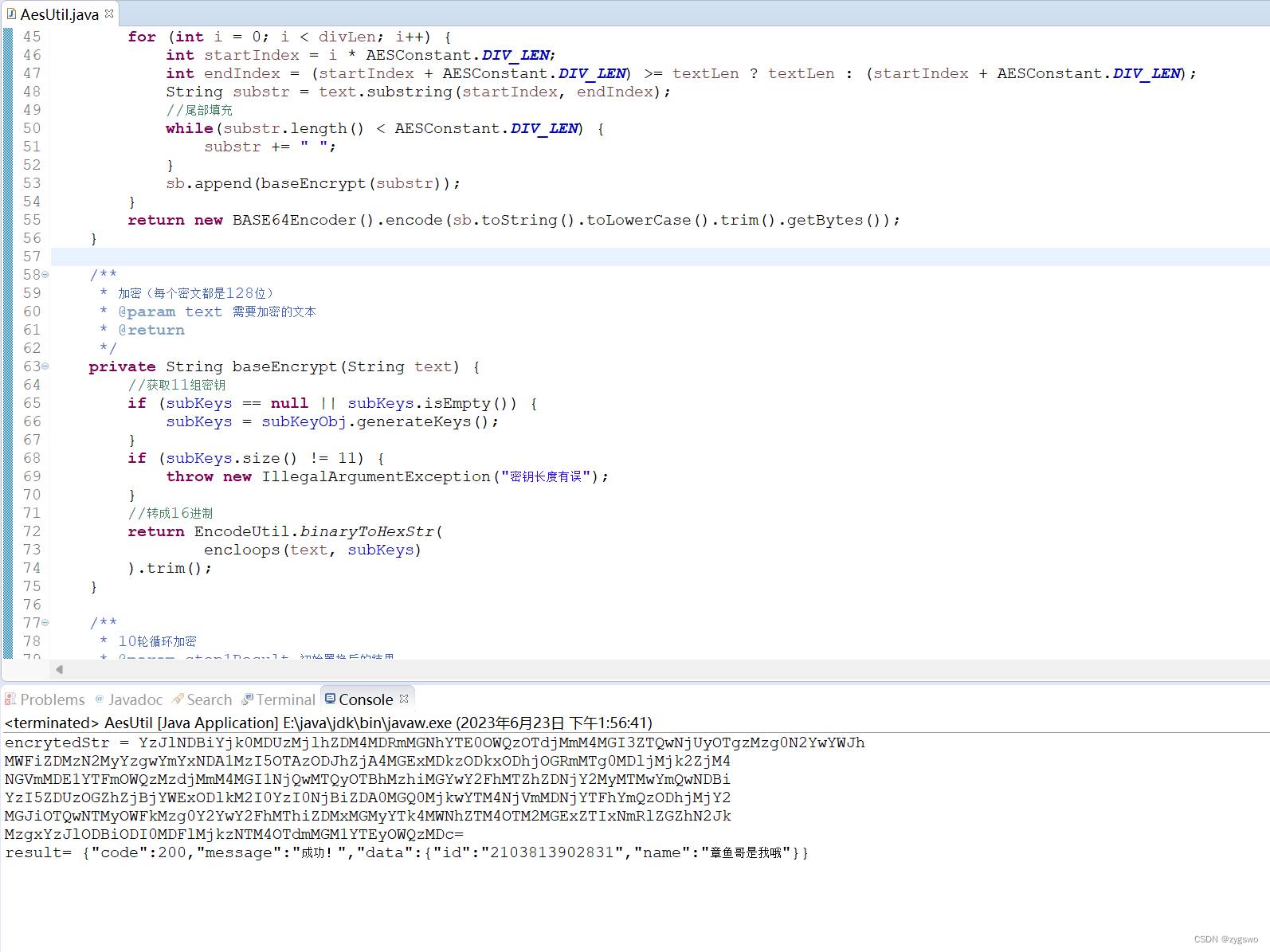
—————————————创作不易，多多支持一下作者，感谢————————
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/码创造者/article/detail/800320
推荐阅读
相关标签
