Prim算法构造最小生成树

Prim算法
普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。
1.问题
举一个实例，画出采用Prim算法构造最小生成树的过程。
2.解析
已知图V = {…} 我们构造一棵最小生成树T
第一步：随意选取起点
第二步：在前一步的基础上寻找最小权值
第三步：继续寻找最小权值，之后以此类推，直到遍历完所有的节点。
实例：
图v如图

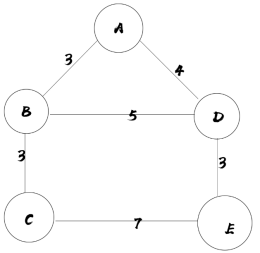
1.任意选择一个点
这里我们选择A点
从A点出发有两条路，一条通向B(权值为3)，一条通向D(权值为4)
我们选择权值较小的点B
此时被选中的点：A B

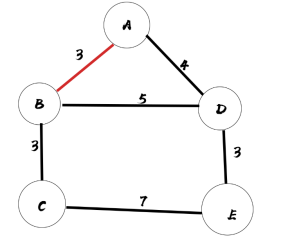
2.找剩下中与以被选中点距离最短的点，判断该点是否被选中，未被选中则选上，直到遍历完所有点。
最终结果如图所示

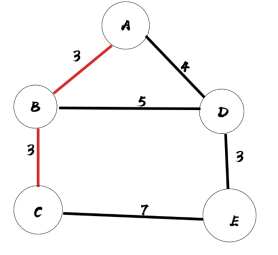
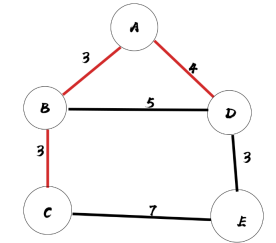
3.设计

void prime(graph g,int s)//最小生成树
{
    int dst[Len];
    int st;
    int minx;
    int sum=0;
    for (int i=0;i<g->nv;++i){
        dst[i]=g->data[s][i];
    }
    printf("V%c ",zd[s]);
    g->visited[s]=1;

    for (int i=1 ;i<g->nv;++i){
        minx=INF;
        for (int j=0;j<g->nv;++j){
            if(minx>dst[j]&&g->visited[j]==0){
                st=j;
                minx=dst[j];
            }
        }
        g->visited[st]=1;
        printf("V%c ",zd[st]);
        sum=sum+minx;
        for (int j=0;j<g->nv;++j){
            if(g->visited[j]==0&&dst[j]>g->data[st][j]){
                dst[j]=g->data[st][j];
            }

        }
    }
    printf("\nthe lowest weight=%d\n",sum);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32