n-皇后问题（DFS问题）_dfs皇后摆放问题

原题题目：

n−皇后问题是指将 n个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

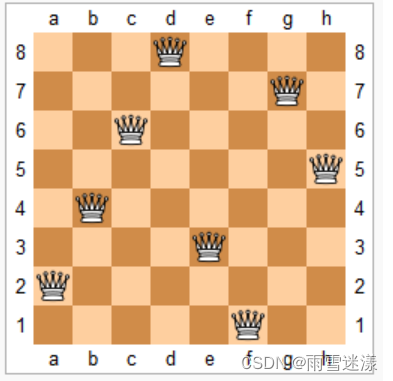
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

题解代码：

 
#include<bits/stdc++.h>
using namespace std;
const int N =20;
char str[N][N];    //用来存储答案
int n;
bool L[N],D[N],FD[N];  //分别存储列，对角线，反对角线的状态
void dfs(int u)
{
    if(u==n)
    {
        for(int i=0;i<n;i++) puts(str[i]);   //对找到的答案进行输出，字符串可以一行一行输出
        puts("");
        return;
    }
    for(int i=0;i<n;i++)
    {
        if(!L[i]&&!D[u+i]&&!FD[n-i+u]) //对列，对角线，反对角线上是否放过Q进行判断
        {
            str[u][i]='Q';
            L[i]=D[u+i]=FD[n-i+u]=true;  //放过Q，把Q位置对应的列，对角线，反对角线状态改变
            dfs(u+1); //下一层
            L[i]=D[u+i]=FD[n-i+u]=false;   //恢复原状
            str[u][i]='.';               //恢复原状
        }
    }
}
int main()
{
      cin>>n;
       for(int i=0;i<n;i++)
       {
           for(int j=0;j<n;j++)
           {
              str[i][j]='.';
           }
       }
       dfs(0);
       return 0;
}
 

代码微解析：

主要解释下面几句代码为什么这样写（主要简述对角线和反对角线与行和列的关系），其余的照搬DFS模板即可。

 if(!L[i]&&!D[u+i]&&!FD[n-i+u])
 
 L[i]=D[u+i]=FD[n-i+u]=true; 
 
 L[i]=D[u+i]=FD[n-i+u]=false;

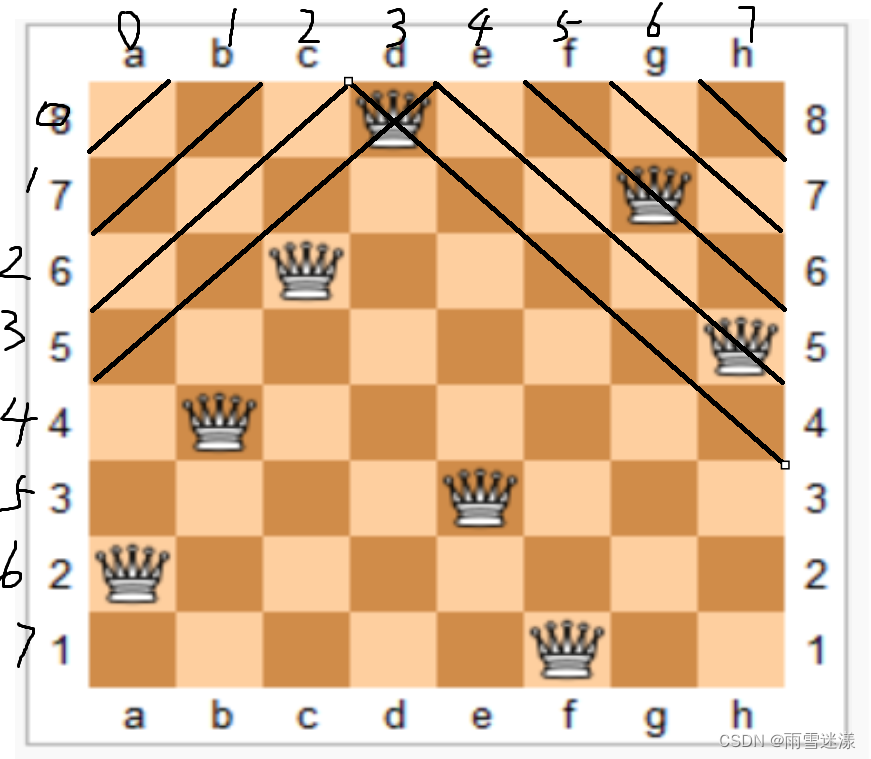
代码中的u是行，i是列。这里有个规律，以第一行皇冠为例。

正对角线（/）：

它的坐标是（3，0），则它对应的正对角线条数是横坐标+纵坐标，D[3+0]（D数组是上面代码中用来存储对角线状态的bool类型数组）,  即第4条对角线。

反对角线（\）：

                                                   //因为起点为0，所以- 1  //从零开始只是为了对应数组下标

而对于反对角线来说，对应（边长-1）(即n的值-1)  + (u(行)   -  i(列) ),同样以第一行的皇冠为例（3，0），FD[7+(0-3)]  （FD数组是上面代码中用来存储反对角线状态的bool类型数组）,  对应反对角线的第5条.