- 1CSS 3 种盒子模型: block, inline, inline-block_css block
- 2Github的注册学习与使用_github 注册 命令规则
- 3Unity 代码控制Animator动画_unity控制animator动画播放
- 4顺序表基础练习(C语言实现)_顺序表题目c语言
- 5阅读A Deeper Look at Machine Learning-Based Cryptanalysis
- 6git和gitee的基本操作
- 7青龙面板+新版傻妞sillyGirl+onebot反向对接傻妞(22年3月2日更新)_青龙反向ws
- 8参数高效微调PEFT(二)快速入门P-Tuning、P-Tuning V2
- 91-13 Docker实战案例_error: unable to find a match: bridge-utils
- 10消息队列数据消失的常见情况,及解决办法_消息队列消息丢失怎么解决
【动手学深度学习】 2预备知识_y.sum().backward()
赞
踩
李沫《动手学习深度学习》课程学习
| 需要预备的知识 | 原因 | 重点 |
|---|---|---|
| 线性代数 | 处理表格数据 | 矩阵运算 |
| 微积分 | 决定以何种方式调整参数 | 损失函数(loss function)—— 衡量“模型有多糟糕”这个问题的分数 梯度(gradient)—— 连结一个多元函数对其所有变量的偏导数,简单理解就是求导 |
| 概率 | 在不确定的情况下进行严格的推断 |
目录
2.1. 数据操作——张量
一个名词——张量(tensor),指n维数组,其中具有一个轴的张量对应数学上的向量(vector); 具有两个轴的张量对应数学上的矩阵(matrix)
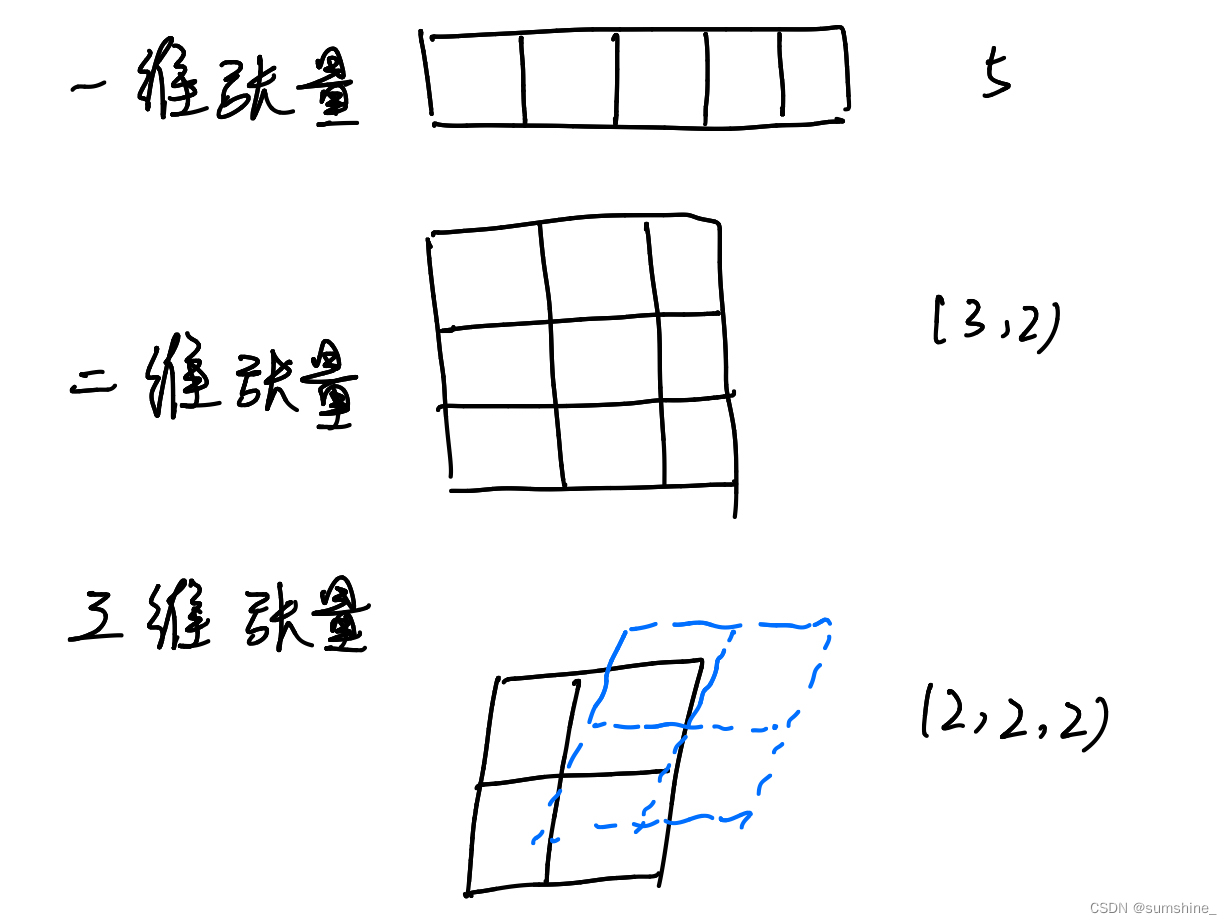
2.1.1. 入门
库名:torch
| 函数名 | 作用 | 例子 | 例子意义 | 结果 |
|---|---|---|---|---|
| arange() | 创建行向量 | torch.arange(12) | 创建了一个包含以0开始的前12个整数的行向量 | tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) |
| zeros() | 设置张量所有元素均为0 | torch.zeros(2,3,4) | 创建一个形状为(2,3,4)的张量,其中所有元素都设置为0 |
|
| ones() | 设置张量所有元素均为1 | torch.ones(2,3,4) | 创建一个形状为(2,3,4)的张量,其中所有元素都设置为1 |  |
| randn() | 随机初始化张量中参数的值 | torch.randn(3,4) | 形状为(3,4)的张量。 其中的每个元素都从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。 | 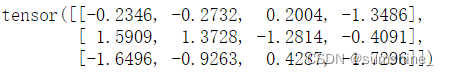 |
| tensor() | 提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值。 在这里,最外层的列表对应于轴0,内层的列表对应于轴1。 | torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]]) | 指定张量 |  |
| 函数名 | 作用 | 例子 | 结果 |
|---|---|---|---|
| shape | 访问张量(沿每个轴的长度)的形状 | x.shape | torch.Size([12]) |
| size() | 访问张量(沿每个轴的长度)的形状 | x.size() | torch.Size([12]) |
| numel() | 张量中元素的总数 | x.numel() | 12 |
| reshape() | 改变一个张量的形状而不改变元素数量和元素值 | x.reshape(3,4) |
|

注:len()函数二维张量时结果与numel()函数相同,三维就不同了
2.1.2. 运算符
——按元素(elementwise)运算
对于任意具有相同形状的张量, 常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算。 我们可以在同一形状的任意两个张量上调用按元素操作。
| 程序中运算函数 | 意义 |
|---|---|
| + | 加 |
| - | 减 |
| * | 乘 |
| / | 除 |
| ** | 幂 |
| torch.exp(input) | 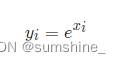 |
| x.sum() x指一个张量 | 对张量中的所有元素进行求和,会产生一个单元素张量 |
| torch.cat(tensons,dim=0/1) 例如:torch.cat((x,y),dim=0),torch.cat((x,y),dim=1) x,y均为(3,4)的张量 | 张量连结(concatenate) dim指张量连接的维度 |
torch.cat 张量连结补充
名词解释:把给定张量端对端地叠起来形成一个更大的张量。

上面的例子分别演示了当沿行(轴-0,形状的第一个元素) 和按列(轴-1,形状的第二个元素)连结两个矩阵时,会发生什么情况。 可以看到,第一个输出张量的轴-0长度(6)是两个输入张量轴-0长度的总和(3+3); 第二个输出张量的轴-1长度(8)是两个输入张量轴-1长度的总和(4+4)
2.1.3. 广播机制
——形状不同的张量通过调用 广播机制(broadcasting mechanism)来执行按元素操作。
广播机制工作方式:复制元素拓展数组,使两个张量具有相同的形状。
拓展方法:在大多数情况下,我们将沿着数组中长度为1的轴进行广播。
例子:a和b分别是3×1和1×2矩阵,如果让它们相加,它们的形状不匹配。 我们将两个矩阵广播为一个更大的3×2矩阵,如下所示:矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。

2.1.4. 索引和切片
——第一个元素的索引是0,最后一个元素索引是-1
| 例子 | 意义 |
|---|---|
| X[-1] | 选择最后一个元素 |
| X[1:3] | 选择第二个和第三个元素 |
| X[0:2,:] | 访问第1行和第2行,其中“:”代表沿轴1(列)的所有元素。 |
2.1.5. 节省内存
低层逻辑:运行一些操作可能会导致为新结果分配内存,机器学习运算量巨大,会导致内存不断被更新占用。
现实意义:节省内存,更重要的是防止需要引用最新值时由于一些问题还是指向了旧值地址,导致错误。
方法:切片表示法,例Y[:] = <expression>
- Z = torch.zeros_like(Y)
- print('id(Z):', id(Z))
- Z[:] = X + Y
- print('id(Z):', id(Z))
-
- output:
- id(Z): 140316199714544
- id(Z): 140316199714544
2.1.6. 转换为其他Python对象
numpy转torch
- A = X.numpy()
- B = torch.tensor(A)
- type(A), type(B)
-
- output:
- (numpy.ndarray, torch.Tensor)
torch张量转标量——item函数或Python的内置函数
- a = torch.tensor([3.5])
- a # tensor([3.5000])
- a.item() # 3.5
- float(a) # 3.5
- int(a) # 3
2.1.8. 练习
-
运行本节中的代码。将本节中的条件语句
X == Y更改为X < Y或X > Y,然后看看你可以得到什么样的张量。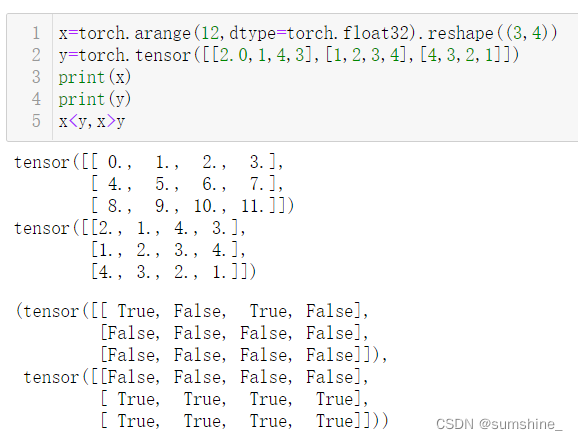
x<y:判断每一个元素是否满足 x<y 的要求,满足为 True,不满足为False ,张量形状为(3,4);x>y:判断每一个元素是否满足 x>y 的要求,满足为 True,不满足为False ,张量形状为(3,4).
-
用其他形状(例如三维张量)替换广播机制中按元素操作的两个张量。结果是否与预期相同
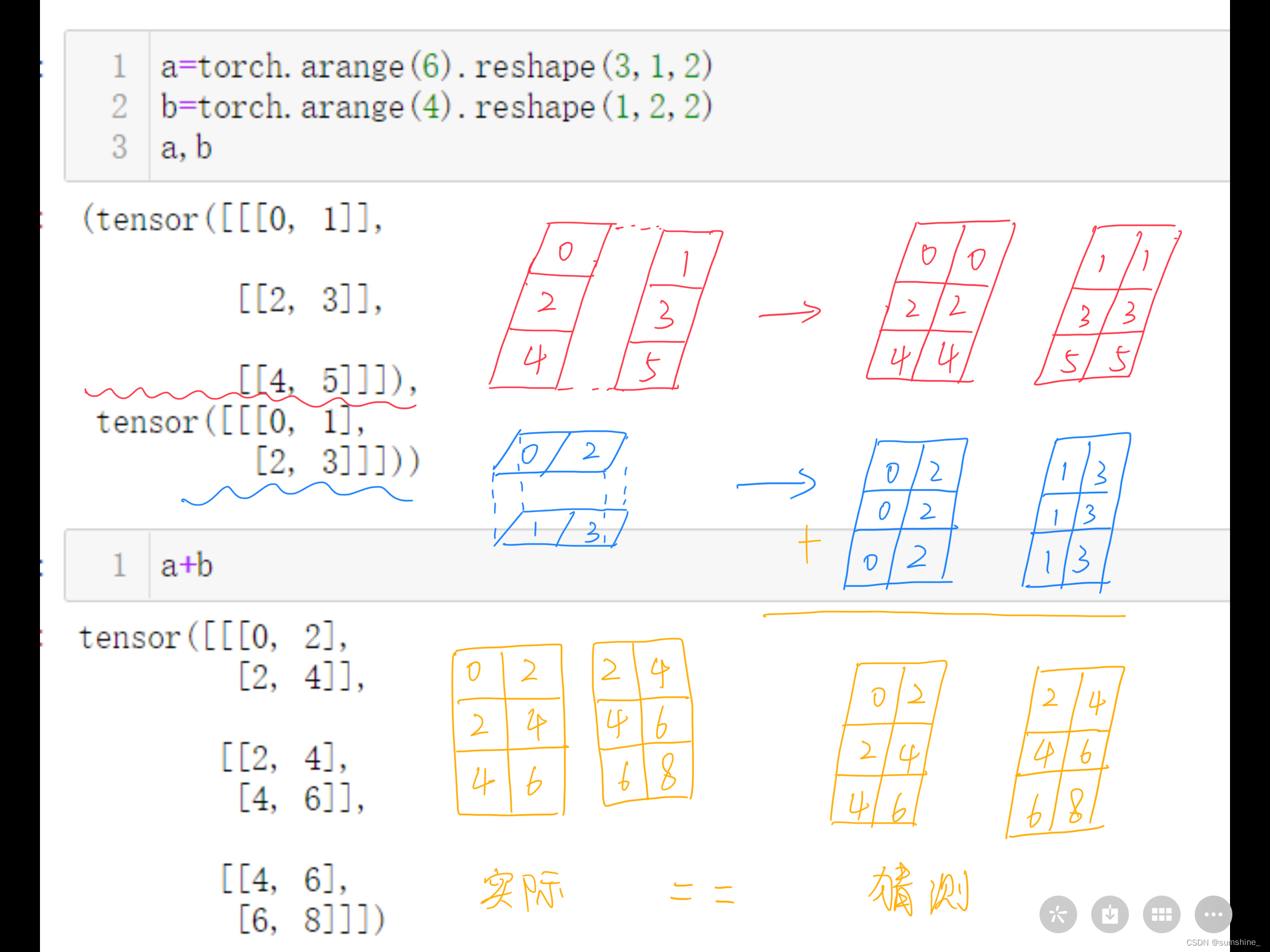
是相同的,但要注意两个问题:
(1) 第3个维度必须相同,否则相加报错
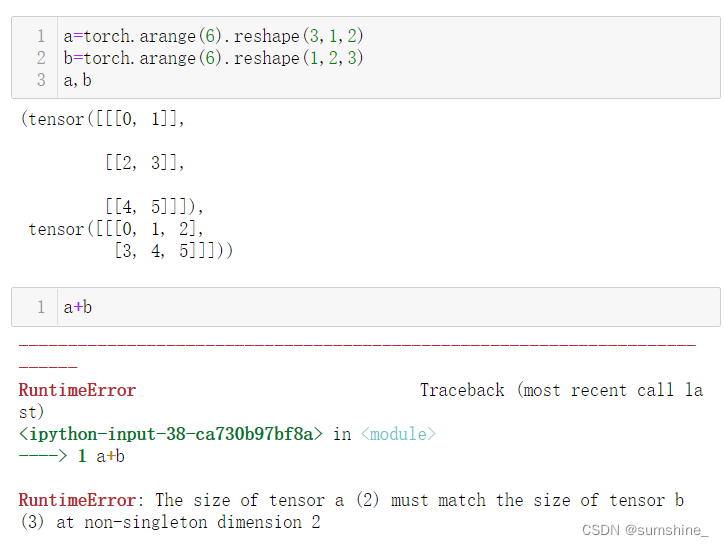
(2)3维tensor元素与几何图之间的对应方法
2.2. 数据预处理
——运用pandas库
注:数据预处理是深度学习中很重要的一部分,pandas库是一个很常用且强大的库,本书中该部分并不是重点,内容较少,在此不总结,会再写一篇文章具体总结pandas库的一些详细用法,并跑几个例程。
2.3. 线性代数
2.3.1. 标量
——包含一个数值的叫标量(scalar)
1、实例

2、数学知识

2.3.2. 向量
—— 一维张量,将标量从零阶推广到一阶
1、实例
2、数学知识

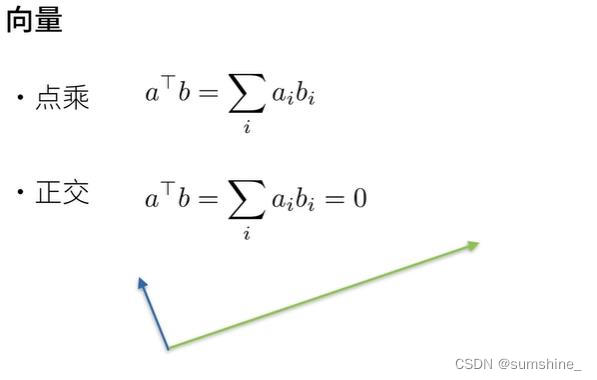
注:点乘、叉乘的区别可以看这 数学基础 —— 向量运算:点乘和叉乘 - 哔哩哔哩 (bilibili.com)
注:点乘和点积(dot product)是一个东西,给定两个向量相同位置的按元素乘积的和。
2.3.3. 矩阵
—— 二维张量,将向量从一阶推广到二阶
1、实例

2、矩阵基础知识
| 代码 | 含义 | 数学解释 |
|---|---|---|
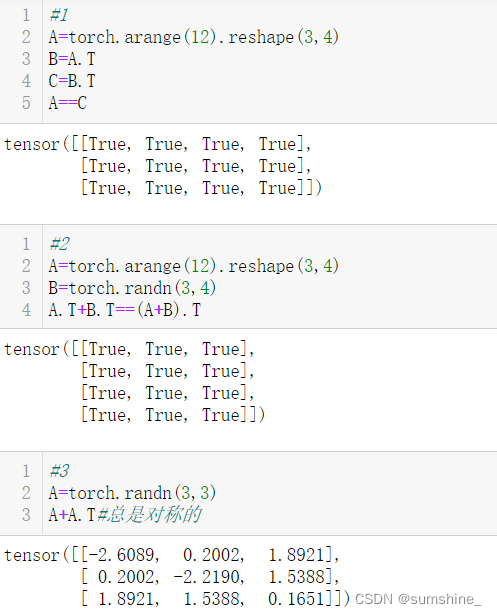
| A.T | 矩阵的转置 | 交换矩阵的行和列 |
| A==A.T结果均为True | 对称矩阵 | Aij = Aji |
| 反对称矩阵 | Aij = -Aji | |
| 正交矩阵 | AAT=E(E为单位矩阵,AT表示“矩阵A的转置矩阵”)或ATA=E | |
| 置换矩阵 | A 是方阵,A 的每一行和每一列都有且仅有一个1,其余均为0 | |
| 方阵 | 矩阵的行数与列数相等 |
补充知识:特征向量与特征值特征值与特征向量 (baidu.com)
3、数学知识
Hadamard积:两个矩阵的按元素乘法
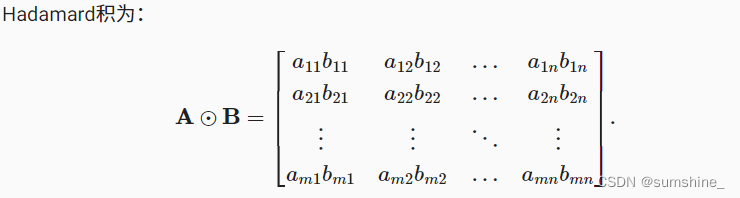
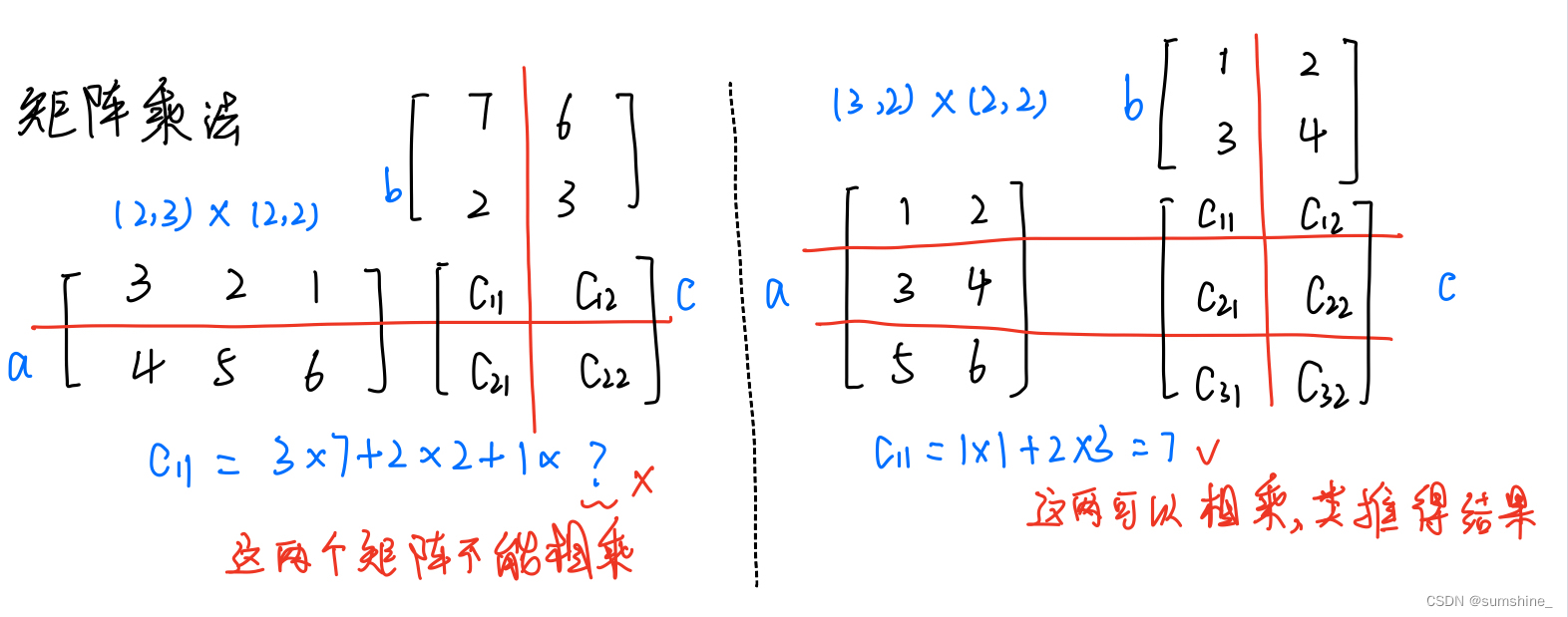
矩阵乘法会对空间进行扭曲,公式不好理解,视频清楚:矩阵乘法的动画演示_哔哩哔哩_bilibili

注:这部分现阶段理解有点困难,先理解向量的概念吧 向量的【范数】:模长的推广,柯西不等式_哔哩哔哩_bilibili
矩阵的【范数】:也是一种长度_哔哩哔哩_bilibili
范数其实可以理解为一种长度,常见L1、L2范数
在深度学习中,我们经常试图解决优化问题: 最大化分配给观测数据的概率; 最小化预测和真实观测之间的距离。 用向量表示物品(如单词、产品或新闻文章),以便最小化相似项目之间的距离,最大化不同项目之间的距离。 目标,或许是深度学习算法最重要的组成部分(除了数据),通常被表达为范数。
4、代码中的函数
| 函数 | 意义 |
|---|---|
| A+B | A、B张量加法 |
| A * B | A、B张量的Hadamard积 |
| torch.dot(x,y) | x,y向量点积 |
| torch.sum(x*y) | 执行按元素乘法,然后进行求和来表示两个向量的点积 |
| torch.mv(A,x) | 矩阵A和向量x的矩阵-向量积,注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。 |
| torch.mm(A,B) | 矩阵A和矩阵B乘法 |
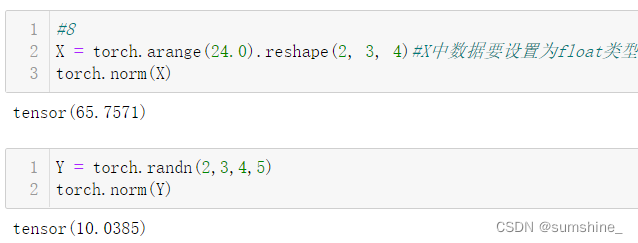
| torch.norm(u) | u张量的L2范数(Frobenius范数) |
| torch.abs(u).sum() | u张量的L1范数,将绝对值函数和按元素求和组合起来。 |
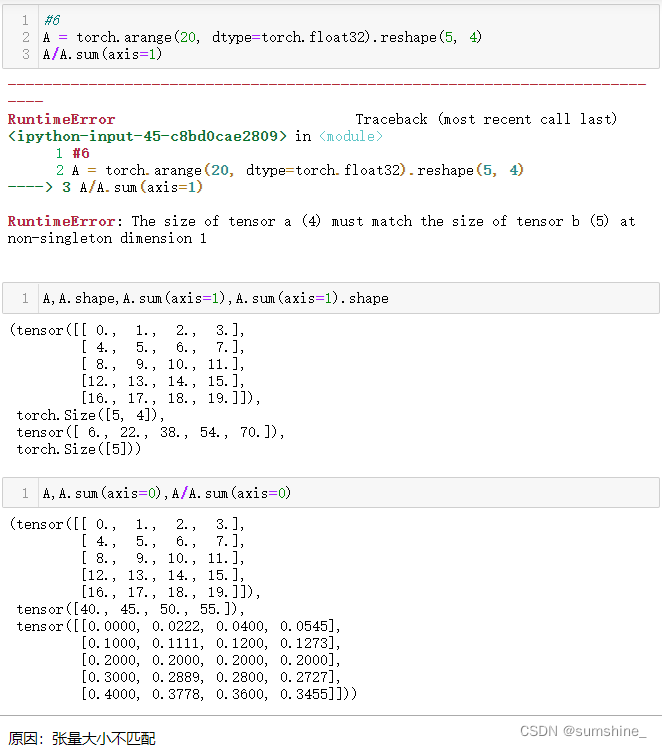
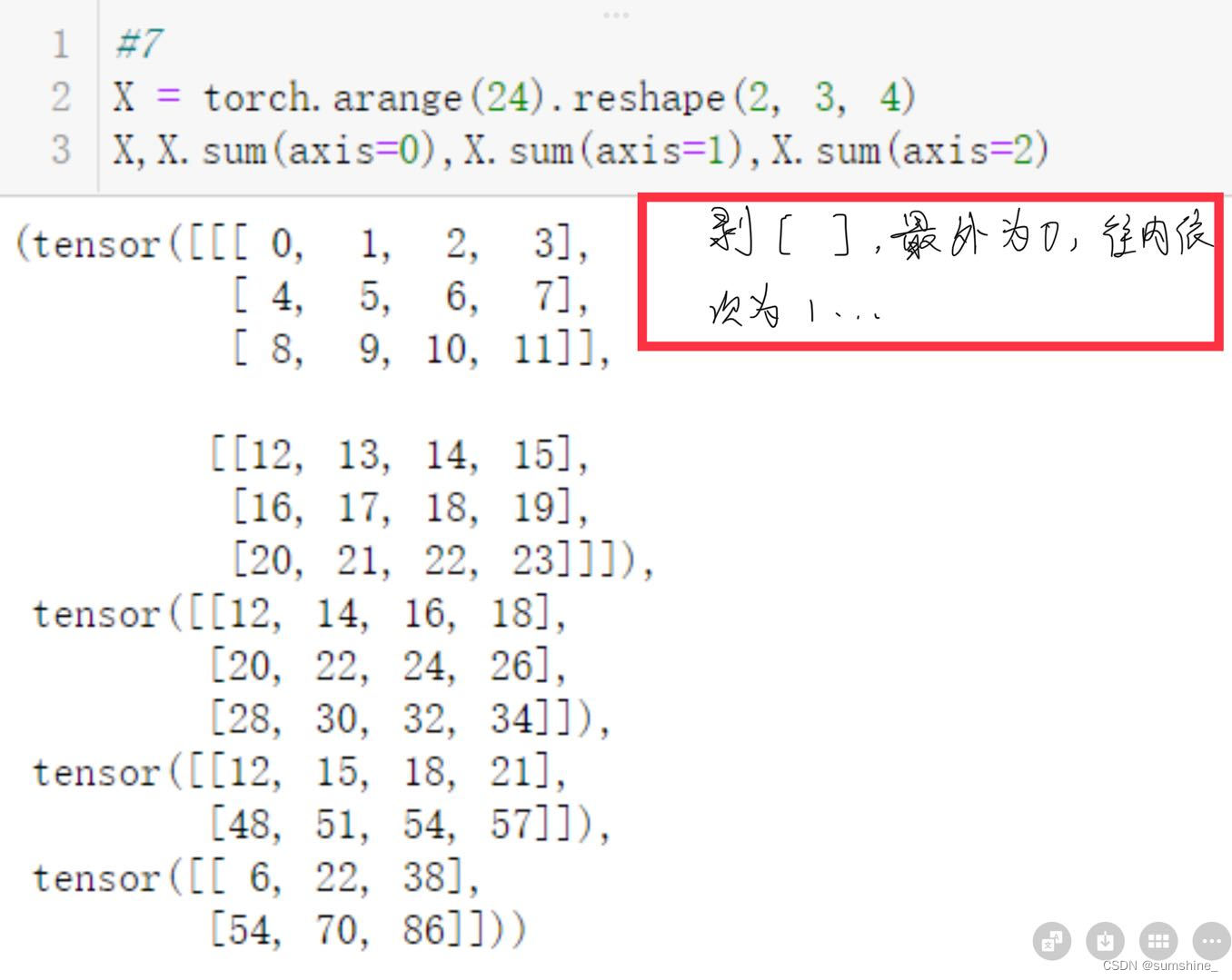
2.3.4. 降维
方法:
1、求和
直接求和——沿所有的轴降低张量的维度,变为一个标量,向量、矩阵均适用

指定张量沿哪一个轴来求和:
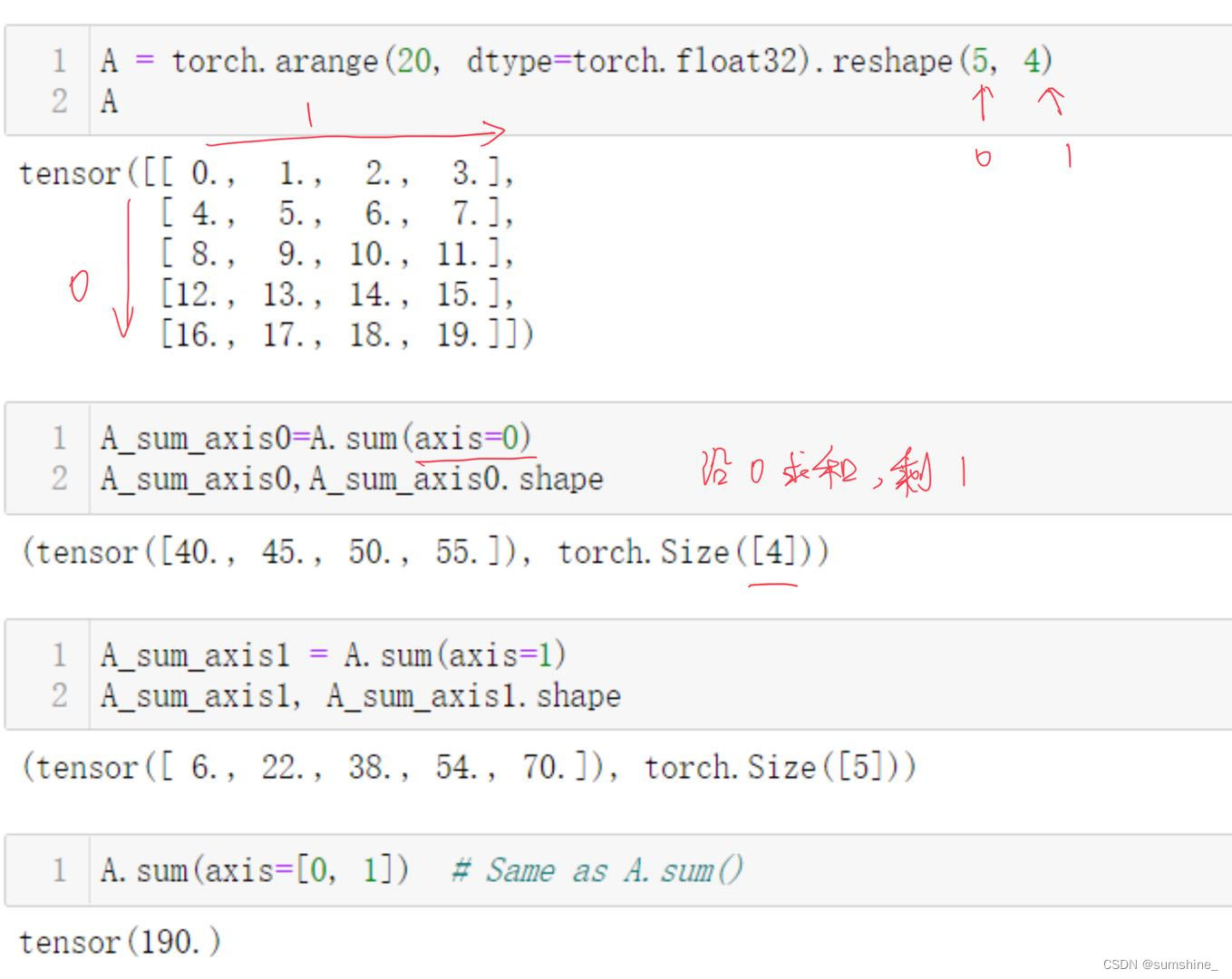
2、求平均
直接求平均:

指定轴:

2.3.4.1. 非降维求和——轴数不变
1、cumsum函数不会沿任何轴降低输入张量的维度。

2、由于sum_A在对每行进行求和后仍保持两个轴,我们可以通过广播将A除以sum_A。

2.3.5. 练习

2.4. 微积分
-
微分和积分是微积分的两个分支,前者可以应用于深度学习中的优化问题。
-
导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率。
-
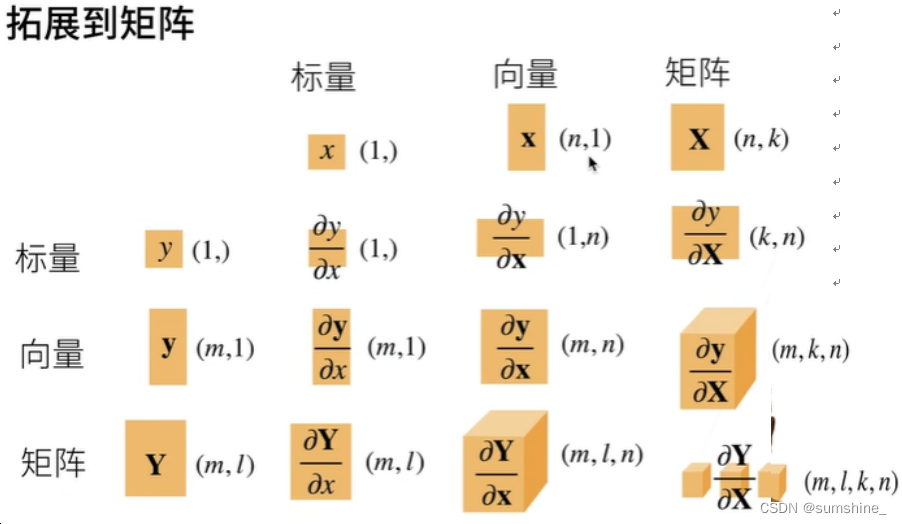
标量关于列向量的导数是一个行向量。
-
列向量关于标量的导数是一个列向量。
-
向量关于向量的导数结果是一个矩阵。
-
梯度是一个向量,指向值最大的方向,其分量是多变量函数相对于其所有变量的偏导数。
-
链式法则使我们能够微分复合函数。
2.5. 自动微分
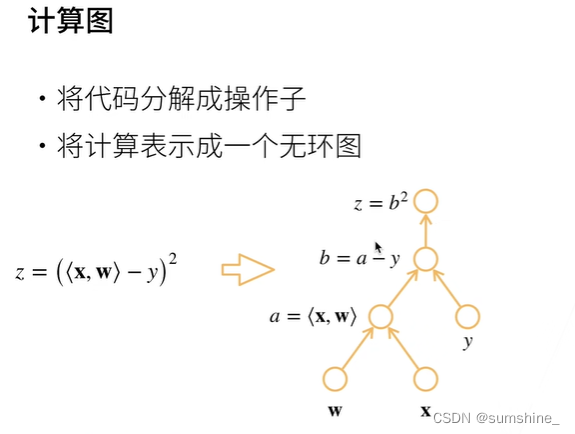
深度学习框架通过自动计算导数,即自动微分(automatic differentiation)来加快求导。 实际中,根据我们设计的模型,系统会构建一个计算图(computational graph),来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播(方向累积)梯度。 这里,反向传播(backpropagate)意味着跟踪整个计算图,填充关于每个参数的偏导数。
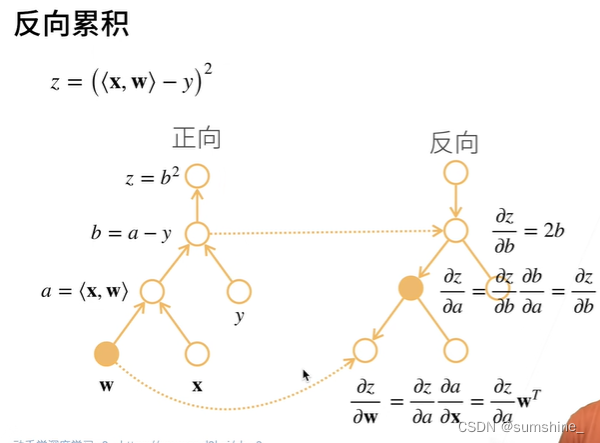
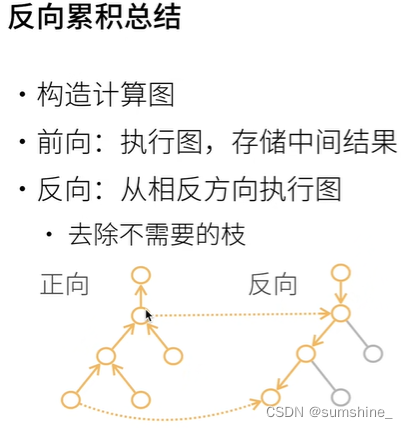
1、backward()反向传播函数和grad函数计算梯度
最基础例子:对函数y=2x⊤x(y等于标量2乘列向量x点积列向量x)关于列向量x求导(按照规则求导后结果为y=4x)
- import torch
-
- x = torch.arange(4.0)
- x
-
- x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True),梯度存的位置
- x.grad # 默认值为None
-
- y = 2 * torch.dot(x, x) # y为标量
- y
-
- y.backward() # 通过调用反向传播函数来自动计算y关于x每个分量的梯度
- x.grad # 打印梯度
在默认情况下,pytorch会累积梯度,单运用同一个变量进行运算,需要清除之前的值,运用下面这行代码
x.grad.zero_()2、非标量变量的反向传播
当y不是标量时,机器学习中通常单独计算批量中每个样本的偏导数之和,如下代码所示。
- # 对非标量调用backward需要传入一个gradient参数,该参数指定微分函数关于self的梯度。
- # 在我们的例子中,我们只想求偏导数的和,所以传递一个1的梯度是合适的
- x.grad.zero_()
- y = x * x
- # 等价于y.backward(torch.ones(len(x)))
- y.sum().backward()
- x.grad
3、运用detach()函数使在系统中函数类型转为常数类型
例子:计算z=u*x关于x的偏导数,同时将u作为常数处理, 而不是z=x*x*x关于x的偏导数。
- x.grad.zero_()
- y = x * x
- u = y.detach()
- z = u * x
-
- z.sum().backward()
- x.grad == u
-
- output:tensor([True, True, True, True])
-
-
- ##由于记录了y的计算结果,可以随后在y上调用反向传播, 得到y=x*x关于的x的导数,即2*x。
- x.grad.zero_()
- y.sum().backward()
- x.grad == 2 * x
-
- output:tensor([True, True, True, True])

4、通过Python控制流(例如,条件、循环或任意函数调用),仍然可以计算得到的变量的梯度。
例子:在下面的代码中,while循环的迭代次数和if语句的结果都取决于输入a的值。
- def f(a):
- b = a * 2
- while b.norm() < 1000:
- b = b * 2
- if b.sum() > 0:
- c = b
- else:
- c = 100 * b
- return c
-
- #计算梯度
- a = torch.randn(size=(), requires_grad=True)
- d = f(a)
- d.backward()
-
- a.grad == d / a
-
- output:tensor(True)

小结:深度学习框架可以自动计算导数,首先将梯度附加到想要对其计算偏导数的变量上。然后记录目标值的计算,执行它的反向传播函数,并访问得到的梯度。
2.6. 概率
-
我们可以从概率分布中采样。
-
我们可以使用联合分布、条件分布、Bayes定理、边缘化和独立性假设来分析多个随机变量。
-
期望和方差为概率分布的关键特征的概括提供了实用的度量形式。





