Android中矩阵Matrix实现平移，旋转，缩放和翻转的用法详细介绍_android matrix

一，矩阵Matrix的数学原理

矩阵的数学原理涉及到矩阵的运算和变换，是高等代数学中的重要概念。在图形变换中，矩阵起到关键作用，通过矩阵的变换可以改变图形的位置、形状和大小。矩阵的运算是数值分析领域的重要问题，对矩阵进行分解和简化可以简化计算过程。对于一些特殊矩阵，如稀疏矩阵和准对角矩阵，有特定的快速运算算法。

在Matrix Matrix中，矩阵的数学原理同样适用。Matrix提供了缩放、平移、旋转和错切等操作，这些操作对应于特定的矩阵变换。例如，缩放操作对应于矩阵的元素乘以一个标量，平移操作对应于矩阵的元素加上一个偏移量，旋转操作则通过矩阵的置换和缩放来实现。

Matrix的数学原理在实际应用中非常重要。在图形处理、计算机视觉、机器学习等领域，都需要使用到矩阵运算和变换。掌握矩阵的数学原理有助于更好地理解和应用这些技术。

二，3x3矩阵的计算方法：

3x3矩阵的计算方法包括加法、减法、数乘和矩阵乘法。

加法是将两个3x3矩阵对应位置的元素相加，得到一个新的3x3矩阵。减法是将两个3x3矩阵对应位置的元素相减，得到一个新的3x3矩阵。数乘是将一个标量和一个3x3矩阵相乘，得到一个新的3x3矩阵。矩阵乘法是将两个3x3矩阵按照一定的规则相乘，得到一个新的3x3矩阵。

在进行矩阵乘法时，需要按照一定的规则进行计算，即左边矩阵的第一行的元素分别与右边矩阵的第一列的元素相乘，然后求和得到相乘矩阵的第一行的第一个元素。同样地，左边矩阵的第一行的元素分别与右边矩阵的第二列的元素相乘，求和得到相乘矩阵的第一行的第二个元素，以此类推。

另外，还有三阶矩阵乘法的公式：D=a11a22a33+a12a23a31+a13a21a32-a13a22a31-a12a21a33- a11a23a32。这个公式可以帮助我们快速地计算出两个3x3矩阵的乘积。

需要注意的是，在进行矩阵运算时，需要遵循一定的运算规则，如先进行括号内的运算，然后进行加、减、乘等运算，最后进行除法运算。同时，要注意矩阵的维数，即行数和列数，只有当两个矩阵的维数相同时才能进行矩阵运算。

三，四种变换的具体情形

1，平移变换
假定有一个点的坐标是 P_(x_0,y_0)将其移动到P_(x,y) ，再假定在x轴和y轴方向移动的大小分别为：
△x = x - x_0
△y = y - y_0
如下图所示：
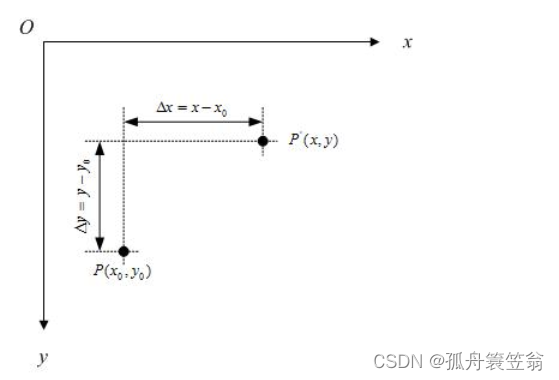不难知道：
x = x_0 + △x
y = y_0 + △y
如果用矩阵来表示的话，就可以写成：

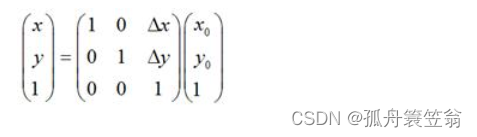
2，旋转变换
围绕坐标原点旋转

假定有一个点的坐标是 P_(x_0,y_0) ，相对坐标原点顺时针旋转 theta后的情形，同时假定P点离坐标原点的距离为r，如下图：
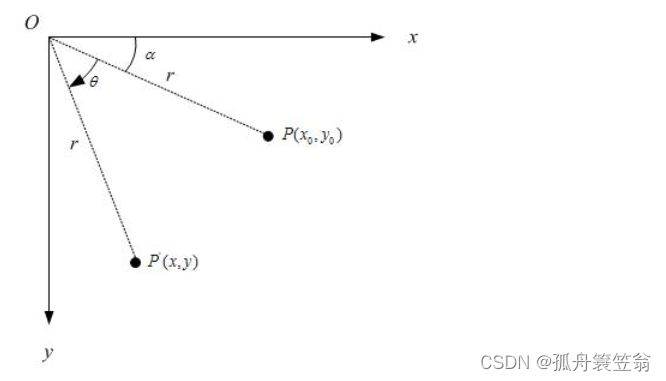那么，
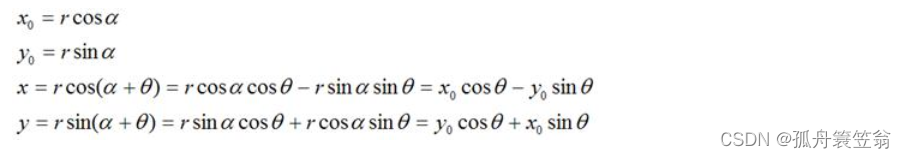如果用矩阵，就可以表示为：
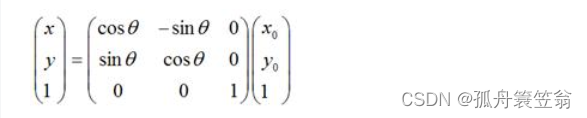3，缩放变换
理论上而言，一个点是不存在什么缩放变换的，但考虑到所有图像都是由点组成，因此，如果图像在x轴和y轴方向分别放大k1和k2倍的话，那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍，即：
x = k_1 x x_0
y = k_2 x y_0

用矩阵表示就是：
4，对称变换（翻转）
事实上，我们还可以利用Matrix，进行对称变换。所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如，某点 经过对称变换后得到，
如果对称轴是x轴，那么，
x = x_0
y = -y_0
用矩阵表示就是：

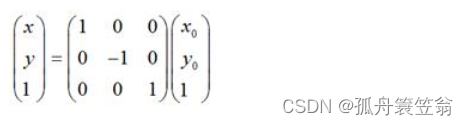
如果对称轴是y轴，那么，
x = -x_0
y =y_0

用矩阵表示就是：
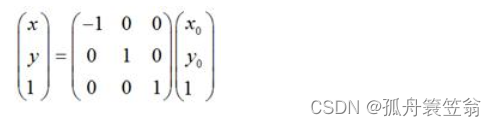如果对称轴是y = x，如图：
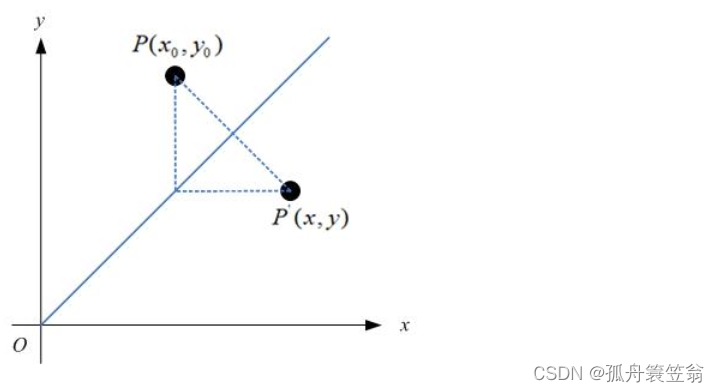四，基本方法解析

1，构造函数

public Matrix()
public Matrix(Matrix src)
1
2

构造函数有两个，第一个是直接创建一个单位矩阵，第二个是根据提供的矩阵创建一个新的矩阵（采用deep copy）

单位矩阵如下：
2，平移效果

public void setTranslate