数学建模算法总结

数学建模常见算法总结

评价决策类模型

层次分析法

层次分析法根据问题的性质和要达到的总目的，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终模型使问题归结为最低层（供决策的方案、措施等）相对于最高层（总目标）的相对重要权值的确定或相对优劣次序的排定

层次分析法建模步骤

建立递阶层次结构模型

构造出各层次中的所有判断矩阵

一致性检验

求权重后进行评价

建立层次结构模型

将决策的目标、考虑的因素（决策准则）和决策方案，按它们之间的相互关系分为最高层，中间层和最低层，给出层次结构图

最高层

决策的目的、要解决的问题（一个要素，目标层）

中间层

考虑的因素、决策的准则（若干个层次、准则层）

最低层

决策时的备选方案（措施层、方案层）

对于相邻的两层

称高层为目标层，低层为因素层

构造判断矩阵

确定各层次之间的权重：从层次结构模型的第2层开始，对于从属于（或影响上）上一层每个因素的同一层诸因素，构造判断矩阵，直达最下层（一致矩阵法）

不把所有因素放在一起比较，而是两两相互比较

对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度

对指标的重要性进行两两比较，构造判断矩阵，进而定出权重

矩阵元素$a_{ij}$的意义是，第$i$个指标相对于第$j$个指标的重要程度[专家经验/领域知识]

第一步

指标量化，指标进行数学化

第二步

指标标准化，一种方法是让总和为1

第三步

判断矩阵法确定权重

一致性检验

因为两两比较的过程中忽略了其他因素，导致最后的结果可能会出现矛盾，所以需要一致性检验

理想化的情况是一致性矩阵：

$a_{ij}\cdot a_{ji}=1$

$a_{ik}\cdot a_{kj}=a_{ij}$

由于人的心理因素，严格的一致矩阵几乎不可能的，因此应当检验我们构造的判断矩阵和一致性矩阵是否有太大差别，在使用判断矩阵求权重之前，必须对其进行一致性检验，只有靠谱的矩阵才能使用

一致性检验的步骤

计算一致性指标$CI=\frac{{\lambda }_{\text{max}}-n}{n-1}$

注

其中特征值可用数学软件计算，若有虚数特征值则取模的最大值

查表获得对应的平均随机一致性指标$RI$

计算一致性比例$CR=CI+RI$

​ 若$CR=0$，则为一致矩阵

​ 若$CR<0.1$,判断矩阵一致，能用

​ 若$CR\ge 0.1$，判断举止不一致，用不了

计算权重

方法一

算数平均法

按列归一化，再求平均值

方法二

几何平均法

求每行的几何平均数，再归一化

方法三

特征值法

求矩阵最大特征值对应的特征向量，再归一化

TOPOSIS方法

图片内的内容如下：

---

TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution），可翻译为通过理想解排序法。国内常简称为优选评分法，能充分利用原始数据的信息，其结果既能客观地反映各评价方案之间的差距。

TOPSIS法引入了两个基本概念：

• 理想解：设想的最优的解，它的各个属性值达到各备选方案中的最好值；
• 负理想解：设想的最劣的解，它的各个属性值达到各备选方案中的最坏值。

方案择优的原则是将各备选方案与理想解和负理想解做比较，若其中有一个方案接近理想解，而同时又远离负理想解，则该方案是诸多方案中最好的方案。TOPSIS通过极大理想解和极小负理想解来完成优选排序。

建模步骤

数据正向化处理（转为极大型指标体系）

数据标准化处理（归一化）

权重确定（AHP、熵权法、默认等比权重）

距离计算

​ 确定最优解和最劣解（经过了正向化处理和标准化处理的评分矩阵Z，里面的数据全部是极大型数据，取出每一列中的最大的数，构成理想最优解向量）

​ 距离计算评分

TOPSIS法是一种理想目标相似性排序法，通过归一化后的数据，找出多个目标中最优目标和最劣目标，计算各评价目标与理想解和负理想解的距离，获得各目标与理想解的贴近度，作为评价目标优劣的依据。

贴近度取值在0～1之间，该值越接近1，表示相应的评价目标越接近最优水平；反之，数值越接近0，表示评价目标越接近最劣水平。

指标统一之后，还需要归一化，以消除量纲的影响，就这样倒也可以，但也可以用我们之前用过的方法，让每列的和为1，或者让每列向量的平方和为1

最后，还需要再确定权重进行评价，此时可以代入层次分析法继续处理。

熵权法

前面说到的指标都带有强烈的主观性，有没有客观的、根据数据本身的性质得到权重的方法呢？

看指标的离散程度，如果某个指标都很接近，则没有太多意义，权重应减小

如果某个指标差距很大，则更好区分，权重应增大

如何表示大家在某个指标上的差距呢？一个思路是用方差确定权重

按照信息论的基本原理的解释，信息是系统有序程度的一个度量，熵是系统无序程度的一个度量。

根据信息熵的定义，对于某项指标，可以用熵值来判断某个指标的离散程度，若信息熵值越小，指标的离散程度越大，该指标对综合评价的影响就越大；如果某项指标的值全部相等，则该指标在综合评价中不起作用。

因此，可利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据。

熵权法是一种客观赋权方法，它可以避免数据本身得出权重。

原理：指标的变异程度越小，所反映的信息量也越少，熵对应的权值也应该越低。

步骤

数据归一化，每列的和应该是1（而不是平方和是1），得到样本所占比重$p_{ij}$

利用信息熵公式求出熵值$e_j=-\frac{1}{\ln n}\sum p_{ij}\cdot \ln p_{ij}$

信息效用值$d_j=1-e_j$

对信息效用值归一化，求出熵权

模糊综合评价法

模糊综合评价法是一种基于模糊数学的综合评价方法

根据模糊数学的隶属度理论它定性评价转化为定量评价，用模糊数学对受到多种因素制约的事物或对象作出一个总体的评价

它具有自我解释、系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决

一个元素是否属于一个模糊集，是用隶属函数$ \mu_A $刻画的 $ (0 \leq \mu_A \leq 1) $

$ \mu_A = 0 $ 表示确定不属于

$ \mu_A = 1 $ 表示确定属于

$ \mu_A = 0.5 $ 时隶属度最强

对于每个因素而言，需确定各自的隶属函数

方法一

模糊统计法。找许多人调查一下，竞赛中没法用

方法二

借助已有的客观尺度。如果领域知识已有相关指标，就直接用。但是注意要归一化到[0,1]区间，归一化可借用TOPOSIS法

方法三

指派法。凭主观意愿指派一个隶属度函数，没有办法的办法，需要能自圆其说

例如

假设微博粉丝数最多1.2亿，则隶属度函数$\mu (x)=\frac{x}{1.2亿}$

颜值直接人工打分

作品质量按10分最优，为了把高分段拉开，用二次函数来拟合$\mu (x)=x^2/100$

作品数量达到40部就已经可以了，隶属度函数$\mu (x)=min(1,x/40)$

得到隶属度之后，确定权重就可以了

权重可以使用前面讲过的熵权法、方差法或判断矩阵法

各种方法的结果有差异，需要选手对结果进行详细分析

事实上，各种方法都可以进行多层次的分析

只需将每一层进一步展开，逐步进行评价即可，甚至可以每层采用不同的评价方法

注意不要为了内容花哨而刻意选择不同方法，而要充分说明为什么选择某一种方法，这种方法的权重是怎么得出来的，权重的大小反映了什么实际意义，如何从数据和结构得到体现的，如果有educated guess（有一句的猜测）的话敏感度如何…

数学规划类模型

问题定义

数学规划

求目标函数在一定约束条件下的极值问题

在给定条件（约束条件），如何按照某一衡量指标（目标函数）来寻求计划、管理工作中的优方案
$$min/maxZ=f(x)$$
$g_i(x)$约束条件（不等式约束、等式约束、整数约束）

线性规划

线性规划（Linear programming），是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，是辅助人们进行科学管理的一种数学方法，是研究线性约束条件下线性目标函数的极值问题的数学理论和方法

线性规划模型三要素

决策变量

问题中要确定的未知量，用于表明规划问题中的用数量表示的方案、措施等，可由决策者决定和控制

目标函数

决策变量的函数，优化目标通常是求该函数的最大值或最小值

约束函数

决策变量的取值所受到的约束和限制条件，通常用含决策变量的等式或不等式表示

多目标规划问题

最优解

所有目标同时达到最优，任何其他解的所有目标都不好于它，一般不存在

有效解

不存在另一个解，所有目标都不比它差，且至少一个目标好于它

满意解

对于每个目标给出阈值，所有目标同时达到即可接受

多目标规划常见的目标函数设定方法

线性加权法

对各个目标线性加权，得到一个综合指标（权值的确定比较tricky）

$ϵ$约束法

设定一个首要目标，其他目标作为约束条件

理想点法

对每个目标设置理想值，使各目标差距的平方和最小

优先级法

首先优化一个首要目标，打平时再考虑次要目标

非线性规划

非线性规划的一般形式
$$
\begin{align}
\min \ & f(x) \
\text{s.t.} \quad &
\begin{cases}
Ax \leq b, \quad A_{eq} \cdot x = b_{eq} & \text{(线性)} \
c(x) \leq 0, \quad C_{eq}(x) = 0 & \text{(非线性)} \
lb \leq x \leq ub
\end{cases}
\end{align}

$$

蒙特卡洛模拟

如果想不到什么更好的方法，就直接随机大量生成向量$[x_1,x_2,x_3,x_4]$，然后观察解的分布

这种方法叫做蒙特卡洛模拟

0-1与整数规划

考虑这样一个问题：现有$$N$$种物品，已知每种物品的重量$w_i$和价值$p_i$，在总重量不超过$W$的前提下，选择若干物品，使总价值$P$最大。

1. 如果每种物品只有一个，如何选择？
2. 如果每种物品有无穷多个，如何选择？

上述规划问题可写成求解$\max P=\sum p_i{x}_i$$，s.t. $$\sum w_i{x}_i\le W$$，$$x_i\ge 0$

这个问题看似线性规划，但要求解$$x_i$$的取值只能是整数，甚至只能是0-1。

没有办法的方法：当成线性规划求解，得出的值假如是小数，再进行微调。

另外的办法：用0-1整数规划的方法求解。

动态规划

动态规划是运筹学的一个分支，通常用来解决多阶段决策过程中最优化问题，基本想法就是将原问题转换为一系列相互联系的子问题，然后通过逐层地求解最终得到最优解。

动态规划理论的前提必须符合下列两个条件：

最优子结构：无法通过去的状态和决策如何，对前面决策所形成的当前状态而言，余下的诸决策必须独立成完整的最优策略，子问题的最优解就是导致这个问题的全局最优。

无后效性：某阶段的状态一旦确定，则此后过程的演变实不会受到此前各状态及决策的影响。即未来与过去无关。

动态规划的组成部分

确定状态

通常用$f[x,y,...]$表示当前最优解

状态转移方程

写出$f[x,y,...]$与$f[x-1,y,...]$之类的关系

初始或边界条件

写出$f[0,0,...]$之类的取值

计算顺序

可能逆序推或顺推

对于背包问题，记$ f(x) $表示只考虑前$x$件物品，在总重量不超过$W$情况下的最优价值。

在0-1背包问题中，若已经求出了考虑前1-$x$件物品的情况，则在考虑第$x$件物品时，可以选择它或者不选择它，取这两种情况下的值较大者。状态转移方程为：

$$f(l,x)=\max [f(l-1,x-w[l])+p[l],f(l-1,x)]$$

边界条件为：$ f(0,x) = 0, f(i,0) = 0, 0 \leq x \leq n $。即重量为0时价值一定为0；考虑0件物品时价值也为0。

计算顺序为从1到$n$, 从1到$W$, 最后输出$f(n,W)$结果即可。

在完全背包问题中，只需做一个调整，在考虑第$i$件物品时，可以选择它的次数为$0-W/w[i]$，且所有背包的价值取这些值的最大值。状态转移方程为：

$$f(l,x)=\max [f(l-1,x-k\cdot w[i])+k\cdot p[i]](0\le k\le W/w[i])$$

启发式算法

什么是启发式算法？人在解决问题时所采取的一种根据经验规则进行发现的方法。

模拟退火SA

模拟退火（SA）的思想借鉴于固体的退火原理，当固体的温度很高的时候，内能比较大，固体的内部粒子处于快速无序运动，当温度慢慢降低的过程中，固体的内能减小，粒子慢慢趋于有序，最终，当固体处于常温时，内能达到最小，此时，粒子最为稳定。

思想

为了不被局部最优解困住，需要以一定概率跳出当前位置，暂时接受一个不太好的解。在搜索最优解的过程中逐渐降温，初期跳出去的概率比较大，进行广泛搜索；后期跳出去的概率比较小，尽量收敛到较优解。

模拟退火的步骤

模拟退火算法的步骤如下：

1）初始化温度$T$(充分大)、温度下限$T_{min}$(充分小)、初始解$X$，每个$T$值迭代次数$L$

2）随机生成临域解$X_{new}$;

3）设$f(x)$函数来计算用来计算解得好坏，计算出$f(X_{new})-f(X)$;

4）如果$f(X_{new})-f(X)>$0，说明新解比原来的解好，则无条件接受，如果$f(X_{new})-f(X$)<0，则说明旧解比新解好，则以概率$e^{((f(X_{new})-f(X))/k*T)}$接受$X_{new}$作为解。

5）如果当前温度<$T_{min}$时，则退出循环，输出当前结果，否则减少当前温度，回到第2步继续循环，常用的降温方法为$T=a\ast T(0<a<1)$，一般取接近1的值。

解空间

解空间就是所有合理解的集合，每次生成的解必须合理

旅行商问题的解空间就是1~~n的全排列

初始解

初始解可以随意选取，但比较好的初始解可以帮助算法尽快收敛可先随机生成少量几个序列，选一个比较小的；或者采用贪心算法选择初始解

目标函数

目标函数根据我们要优化的目标确定，旅行商问题的目标函数就是路径长度

降温方法

初始温度、降温方法的选择没有固定标准，只能试例如初始温度为1，每次降温就乘以99%，降到10^-30就停止需要根据具体问题的数值，能接受的迭代次数等确定

注：也不需要每次迭代都降温，也可以迭代几次才降一次温

温度和接受概率的关系

根据模拟退火算法，如果新解更差了，那就以$ e^{\frac{\Delta f(x)}{T}}$的概率接受可见，如果温度较高，新解变差的程度不大，则接受的概率较大

如何生成新的解

新解的生成是最体现创造性的地方，可以自己提出如何将当前解变换为新解，而且保证新解是合理的，并且和旧解的差异不要太大

例如：

任意选择两个标号，调换位置

任意选择两个标号，颠倒它们中间的序列

任意选择三个标号，将前两个标号之间的序列放到第三个标号之后

遗传算法CA

遗传算法是一种基于自然选择原理和自然遗传机制的搜索（寻优）算法，它是模拟自然界中的生命进化机制，在人工系统中实现特定目标的优化。

突变和基因重组是进化的原因，遗传算法是通过群体搜索技术，根据适者生存的原则逐代进化，最终得到准最优解。

其基本思想是根据问题的目标函数构造一个适应度函数（Fitness Function），对种群中的每个个体（即问题的一个解）进行评估（计算适应度）、选择、交叉和变异，通过多轮的繁殖选择逐渐形成好的个体作为问题的最终解。

操作包括：初始群体的产生，求每一个体的适应度，根据适者生存的原则选择优良个体，被选出的优良个体两两配对，通过随机交叉与某些个体的基因片段随机变异某些染色体的基因生成下一代群体，按此方法使群体逐代进化，直到满足进化的终止条件。

步骤

产生$M$个初始解，构成初始种群

每对父母以一定概率生成一个新解（交配产生后代）

每个个体以一定概率发生变异（即将自己的解变动变产生新解）

父代和子代合在一起，留下$M$个最好的个体进入下一轮，其余淘汰（进行自然选择）

重复以上迭代，最后输出最好的个体

如何选择参数

遗传算法中要选择的参数很多：种群数量$S$、变异概率、生成子代的数量、迭代次数

但很遗憾，参数的选择没有固定标准，只能自己试

种群数量M越大，迭代次数越多，生成的子代越多，当然更有希望找到最优解，但相应的计算资源消耗也会增大，只能在可接受范围内进行选择

如何选择初始种群

其实可以随便初始化，但是较好的初始种群可以帮助更快收敛

例如随机生成若干个选最好的、贪心算法等

如何交配产生子代

交配方法应该尽量继承父代，但也要进行足够的调整

例如：

选择父亲的一个标号$t$，在母亲那里找到它后面的全部数字，并依序取出

把父亲标号$t$后面的部分接到母亲后面

把母亲取出来的数字接到父亲后面

如何突变产生新的解

突变就是根据自己的解生成一个新的解，方法可以和模拟退火中的方法相同

蚁群算法ACO

蚁群算法来自于蚂蚁寻找食物过程中发现路径的行为。蚂蚁并没有视觉却可以寻找食物，这得益于蚂蚁分泌的信息素。蚂蚁之间相互独立，彼此之间通过信息素进行交流，从而实现群体行为。

蚁群算法的基本原理就是蚂蚁觅食的过程。首先，蚂蚁在觅食的过程中会在路径上留下信息素（pheromone），并在寻找食物的过程中感知这种物质的强度，并指导自己的行为方向，他们总会朝着浓度高的方向前进。

因此可以看得出来，蚂蚁觅食的过程是一个正反馈的过程，该路段经过的蚂蚁越多，信息素留下的就越多，浓度越高，更多的蚂蚁都会选择这个路段。

步骤

蚁群算法的步骤如下：

选择蚂蚁的数量。每个蚂蚁随机选择一个起点，初始化所有路线上信息素的浓度相等

每一个蚂蚁从不同点出发，依次选择自己的路径

​ 在每一个节点处，根据路径本身信息$\eta$和信息素浓度τ选 择下一个节点

​ 选择每个节点的概率正比于${\tau }^{\alpha }{\eta }^{\beta }$

选择自己的路径后，在被选择路径上留下信息素$\Delta \tau =\frac{q}{路径长}$

每一轮的信息素会以一定比例挥发，更新信息素浓度τ = $p{\tau }_0+\Delta \tau$

重复以上迭代若干次，输出找到最优的解

需要选择哪些参数

蚂蚁的数量：一般蚂蚁的数量和顶点数量一样就可以

迭代的次数：根据计算资源选择

$ \alpha, \beta $：影响路径本身信息和信息素浓度的相对重要性

挥发系数 ( $\rho KaTeX parse error: Can't use function '\)' in math mode at position 1: \̲)̲、信息素总量 \( Q$ )：只能根据具体问题来试

图论算法

基本概念

如果我们能用点表示某事物，用点与点之间的线表示事物之间的联系，就要可以把这件事物抽象地使用图表示出来。而运用抽象的方式将问题抽象为图，并为之建立的数学模型，就是图论

图的基本元素

顶点

用点集$V$表示，$V$=$v_1,x_2,...,v_n$

边

用边集$E$表示，$E$=$e_1,e_2,...,e_m$

权重

点$i$到点$j$的边权记为$w_{ij}$

图

顶点和边的几何，$G=(V,E)$

图的基本概念

边如果是单向箭头，表示有方向，构成有向图，构成的图称为有向图

如果没有箭头，只要线，表示双向，构成的图称为无向图，比如通信电缆

权重不仅可以表示长度，也可以表示时间、费用等概念

边的表示方式

边列表

邻接表

邻接矩阵

最小生成树

最小生成树问题 (Minimum spanning tree problem)

最小生成树问题也是一种常见的图论问题，路线路设计、道路规划、电网布置、公交通线、网络设计，都可以转化为最小生成树问题。如果要求总线路长度最短、材料最少、成本最低、耗时最少等，转换为最短路径问题，最小生成树是保证覆盖一个标的图所有的顶点的连通树，但不能确保连通两点之间的距离最短。

连通图： 在无向图中，若任意两个顶点v与j之间有路径相连，则称该无向图为连通图。

强连通图： 在有向图中，若任意两个顶点v与j之间都有路径相连，则称该有向图为强连通图。

连通网： 一个连通图，当每条边都有一定的权值时，每一条边都应有一个权，称为“网络”，权代表连接两点的距离、时间、成本等。

生成树： 一个连通图的生成树是指包含该图的所有顶点，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。对于一个n顶点的连通图，其生成树有且仅有n-1条边，如果生成树含有n-1条边，则必定生成一个连通图。

最小生成树： 在连通图的所有生成树中，所有边的代价和最小的生成树，称为“最小生成树”。

针对一个连通图，选择n-1条边，把n个顶点全部连起来，且边长度综合最短

实际问题

要在n个居民点之间架设煤气管道，使造价最小

在某个区域内的城市间修建公路，以使任意两个城市间能够直接或间接到达

算法1（prim算法）

适合边多点少的情况，图采用邻接矩阵存储

找到目前情况下能连上的权值最小的边的另一端，加入之，直到所有的顶点加入1

算法2（kruskal）

适合边少点多的情况，图采用边目录方式存储

选目前情况下能连上的权值最小的边，若与生成的树不够成环，加入之，直到n-1条边加入完毕

最短路径问题（SPP）

最短路径问题 (Shortest path problem)

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由节点和路径组成的）中两节点之间的最短路径。根据初始条件的不同，可分为五种常见情况：最短路径问题： 旨在寻找图中两节点之间的最短路径；

确定起点的最短路径问题： 即已知起点，求最短路径的问题；

确定终点的最短路径问题： 与确定起点的问题相反，该问题是已知终点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题；

确定起点终点的最短路径问题： 即已知起点和终点，求两点之间的最短路径；

多目标最短路径问题： 求图中任意两点间的最短路径，也可以合并为一种情况——全局最短路径问题，只要某出全局最短路径，那其余四种情况也已经包含在内了。

最短路径（Shortest path）

想要从一个顶点走到另一个顶点，最短的路径是什么？

单源最短路

起点是确定的，求出这个起点到其他终点的最短路径

多源最短路

求出从所有起点到其他店的最短路径

Dijkstra算法（单源最短路径）

从起点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问的顶点的邻接节点，直到扩展到终点为止

Floyd-Warshall（多源最短路径）

利用动态规划的思想，时间复杂度高，适合计算多源最短路

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大

b.对于每一对顶点$u$和$v$，看看是否存在一个顶点$w$使得从$u$到$w$再到$v$比已知的路径更短

如果是更新它

最短路径的常用算法

图的规模小，则用Floyd。若边的权值有负数需要判断负圈

图的规模大，且边的权值非负，用Dijkstra

图的规模大，且边的权值有负数，用SPFA，需要判断负圈

其他图论算法

关节点（割点）

如果连通图去掉某个点和与它相连的所有边，整个图将变得不连通

桥

如果连通图去掉某条边，整个图将变得不连通

连通分量

如果连通图去掉某条边，整个图将变得不连通

团

若一些顶点两两都相连，则构成一个团

社区

将顶点分成若干组，组内边的数量大于组间边的数量

二分图

顶点可分为两组，每组顶点内部没有变相连

二分图匹配

在一个二分图内找出一些边，使得任何一个图中的点都被至多一条边连接

网络流

顶点之间的边表示最大流量（有向），求从一个顶点到另一个顶点的最大流量

拓扑排序

每个顶点表示一项任务，边表示任务的前后关系，给出顶点排序，使其不违背给定的前后关系

关键路径

关键路径（critical path）：已知一些活动的持续时间和前后关系，求最短完成时间

顶点表示时间，边表示活动

从起点到终点，最长的一条路称为关键路径，上面的活动称为关键活动

关键活动没有拖延余地，一旦关键活动拖延，总时间一定延后

求解方法

先要拓扑排序

从前到后写出最早时间，即所有紧前工作都能完成的最早时间

从后到前写出最晚时间，即所有紧后工作都要开始的最晚时间

如果最早=最晚，则该顶点在关键路径上

回归模型

回归模型问题概述

在统计学中，回归分析指的是确定的两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，这是一种预测性的建模技术，通常用于预测分析以及发现变量之间的因果关系

回归模型正是表示从输入变量到输出变量之间映射的函数，回归问题的学习等价于函数拟合：选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据

回归分析的一般步骤

1）收集一组包含因变量和自变量的数据；

2）选定因变量与自变量之间的模型，利用数据按照最小二乘准则计算模型的系数；

3）利用统计分析方法对不同的模型进行比较，找出与数据拟合得最好的模型；

4）判断得到的模型是否适合于这组数据，诊断有无不适合回归模型的异常数据；

5）利用模型对因变量作出预测或解释；

按照自变量的多少分为：一元回归分析和多元回归分析；

按照因变量的多少分为：简单回归分析和多重回归分析；

按照自变量和因变量之间的相关关系不同分为：线性回归分析和非线性回归分析

线性回归

研究内容

研究自变量x和因变量y之间的相关性（回归分析只能研究相关性而不能研究因果性）

适用数据

连续数值变量

分类

一元线性回归

如果研究的线性函数只包含一个自变量和因变量，且二者的关系可以用一条直线刻画时，这种回归就是一元线性回归

多元线性回归

如果涉及两个以上的自变量，且是线性关系，就称为多元线性回归

一元线性回归

一元线性回归模型
$$y={\beta }_0+{\beta }_{1}x+u$$
$u$称为误差项或随机项，该方程表示，当 $x $=$ x_0$ 时，$E(y)={\beta }_0+{\beta }_1{x}_0$

${\beta }_0$、${\beta }_1$是回归系数

线性回归的目标是找到最优的系数${\beta }_0$, ${\beta }_1$, ${\beta }_2$, $\dots$, ${\beta }_p$,使得模型预测的值与真实值之间的误差最小。

这个误差通常用残差平方和来表示：$RSS=\sum (y_i-\widehat{y_i}{)}^2$

许多非线性方程也可以化为线性方程的形式：例如
y = a x b → ln ⁡ y = ln ⁡ a + b ln ⁡ x y = a e b x → ln ⁡ y = ln ⁡ a + b x y = a + b ln ⁡ x → 以 ln ⁡ x 做自变量 y = a − b x → 以 1 x 做自变量 y = a e − b x → ln ⁡ y = ln ⁡ a − b x y = 1 1 + e a − b x → ln ⁡ ( 1 y − 1 ) = a − b x

$$\begin{aligned} y &= ax^b \rightarrow \ln y = \ln a + b \ln x \\ y &= ae^{bx} \rightarrow \ln y = \ln a + bx \\ y &= a + b \ln x \rightarrow \text{以} \ln x \text{做自变量} \\ y &= a - \frac{b}{x} \rightarrow \text{以} \frac{1}{x} \text{做自变量} \\ y &= ae^{-\frac{b}{x}} \rightarrow \ln y = \ln a - \frac{b}{x} \\ y &= \frac{1}{1 + e^{a - bx}} \rightarrow \ln \left(\frac{1}{y} - 1\right) = a - bx \end{aligned}$$ yyyyyy​=axb→lny=lna+blnx=aebx→lny=lna+bx=a+blnx→以lnx做自变量=a−xb​→以x1​做自变量=ae−xb​→lny=lna−xb​=1+ea−bx1​→ln(y1​−1)=a−bx​

最小二乘法

原理

基于最小化误差的平方和来寻找数据的最佳函数匹配，用于估计未知参数，使得预测值与实际观测值之间的误差平方和最小

应用场景

最小二乘法是解决曲线拟合问题最常用的方法。在已知一组数据点的情况下，可以利用最小二乘法求得一条最能代表这些数据的曲线

求解未知量

最小二乘法可以用于求解未知量，使得误差值最小。例如，在回归分析中，可以利用最小二乘法求得回归直线的斜率和截距，使得预测值与实际值之间的误差平方和最小

前提条件

最小二乘法成立的前提条件是假设系统中无系统误差，误差均为偶然误差，并且假设误差符合正态分布，即整个系统最后的误差均值为零

计算过程

对于一元线性回归，假设有n个数据点($x_i,y_i$)，其中$i$从1到$n$。我们的目标是找到一条直线$y$=$ax+b$，其中$a$是斜率，$b$是截距。最小二乘法的目标是最小化以下误差平方和：
$$S=\sum _{i=1}^n{\left(y_i-(a{x}_i+b)\right)}^2$$
为了找到使$S$最小的$a$和$b$的值，我们需要对$S$求关于$a$和$b$的偏导数，并令它们等于零。这样可以得到一个线性方程组，解这个方程组就可以找到最优的$a$和$b$

评判标准

相关系数 $r^2=\frac{l_{xy}^2}{l_{xx}{l}_{yy}}$越大，说明自变量与因变量的关系越强。

总离差平方和： $SST=\sum {\left(y_i-\bar{y}\right)}^2=l_{yy}$

回归平方和： $SSE=\sum {\left(\widehat{y_i}-\bar{y}\right)}^2=\frac{l_{xy}^2}{l_{xx}}$

残差平方和： $ SSR = \sum \left(y_i - \hat{y_i}\right)^2 = \sum u_i^2$

可以证明 $SST=SSE+SSR$

拟合优度 $R^2=\frac{SSE}{SST}=1-\frac{SSR}{SST}$ 可以理解为 $y$ 能被 $x$ 解释的百分比

预测

要想估计$x_0$对应的$y_0$

估计$E(y_0)$，统计量为$T=\frac{\widehat{y_0}-E(y_0)}{\hat{\sigma }\sqrt{\frac{1}{n}+\frac{(x_0-\bar{x}{)}^2}{l_{xx}}}}\sim t(n-2)$

估计$y_0$，统计量为$T=\frac{\widehat{y_0}-y_0}{\hat{\sigma }\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x}{)}^2}{l_{xx}}}}\sim t(n-2)$

可见，$$x_0$$ 与 $$\bar{x}$$ 的偏差越大，估计所得范围越宽。
若 $$n$$ 足够大，$$x_0$$ 与 $$\bar{x}$$ 的偏差也不太大，可近似取
$$Z=\frac{\widehat{y_0}-y_0}{\hat{\sigma }}\sim N(0,1)$$

多元线性回归

如果人们根据知识、经验或者观察等，认为与因变量 $$y$$ 有关联性的自变量不止一个，那就应该建立多元线性回归模型。

方程形式：$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+u$$

最小二乘法 (OLS)：$$\min Q({\beta }_0,{\beta }_1,\cdots )=\sum {\left[y_i-({\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_k{x}_{ik})\right]}^2$$

F.O.C.
$$\frac{\partial Q}{\partial {\beta }_0}=-2\sum \left[y_i-({\beta }_0+{\beta }_1{x}_{i1}+\cdots )\right]=0$$
$$\frac{\partial Q}{\partial {\beta }_j}=-2\sum x_{ij}\left[y_i-({\beta }_0+{\beta }_1{x}_{i1}+\cdots )\right]=0$$

矩阵形式的方程：$$Y=X\beta$$，$$\min Q(\beta )=\Vert Y-X\beta \Vert$$

系数向量可利用 $$X^{T}Y=X^{T}X\beta$$ 求解

拟合优度 $$R^2=\frac{SSE}{SST}=1-\frac{SSR}{SST}$$

调整后 $$R^2=1-\frac{SSR/(n-k-1)}{SST/(n-1)}$$

分类变量的处理

如果某个变量属于分类数据，例如季节、学历、职务、房屋朝向等，不应该用0、1、2等表示，因为0与1、1与2的差不表示任何含义。

此时应当拆分成多个0-1变量进行处理，以季节为例，应该设3个变量：

注意变量的数量必须比类别的数量少1，否则会出现多重共线性问题。

注：除此之外，如果两个变量强相关，也会出现多重共线性，应考虑剔除其中一个

在多元线性回归中，需谨慎选择回归变量，使F比或调整后 ( R^2 ) 等统计量最大化，留下的系数都显著。

枚举全部情况过于繁琐，可采用逐步回归的方法：

1）每次引入一个新变量，这个变量的系数应该显著，而且应该使统计量增加最大

2）引入一个新变量后，立即检查是否有统计量可删除

3）从影响最小的统计量开始删除，直至删除全部可删除的变量

4）重复以上过程，直至没有统计量可再次引入

非线性回归

根据问题的实际背景，有时已知回归方程的具体形式，且无法化为线性回归的形式，此时只能采用非线性回归，利用最小二乘法求出待定系数

有监督和无监督分类模型

分类任务

不管是分类，还是回归，其本质是一样的，都是对输入做出预测，都是对输入做出预测，并且都是监督学习。说白了，就是根据特征，分析输入的内容，判断它的类别，或者预测其值

有监督分类算法

有监督分类问题

训练算法的主要目标是建立具有很好泛化能力的模型，即建立能准确预测未知样本类标号的模型

首先需要一个训练集（training set），由类标号已知的记录组成，使用训练集建立分类模型，然后将模型运用于检验集（test），由类标号未知的记录组成

训练集与检验集的划分方法

留出法

取较大比例的数据做训练集，较小比例的数据做测试集，只用训练集进行训练

交叉验证法（k折法）

将数据分成k份，每次用其中k-1份做训练，另外1份做测试

自助法

有放回抽样N次，用作训练集，没被抽到的数据用作测试集

训练误差

模型在训练集上的误差

泛化误差

模型在测试集上的误差

欠拟合

模型过于简单或迭代次数不够，没学到数据的真实结构，训练误差和泛化误差都很大

过拟合

数据过少，模型太复杂或迭代次数过多，训练误差很小，但泛化误差太大

评价指标

对于二元分类问题而言，可以建立混淆矩阵

准确率

预测正确的比例
$$accuracy=\frac{TN+TP}{TN+FP+FN+TP}$$

查准率

预测类1当中，有多少真的是类1
$$\frac{TP}{TP+FP}$$

查全率

实际类1当中，有多少预测出来了
$$\frac{TP}{TP+FN}$$

F1-score

Precision（准确率）和Recall（查全率）的综合指标
$$\frac{2\times Precision\times Recall}{Precision+Recall}$$

ROC-AUC

预测模型最后实际上给出的是一个属于类1的概率p

数据分析分析人员需要根据实际情况判断p大于多少的时候，认为是类1

p越大，则判断越严格，查准率越高，但查全率越低

当p取不同值的时候

Precision和Recall的图像就是P-R曲线，二者相等的取值称为平衡点

TPR($\frac{TP}{TP+FN}$)和FPR($\frac{FP}{TN+FP}$)的图像就是ROC，ROC下方的面积就是AUC

对于多类问题，可以先单独挑出一个类，写出这个类相当于其余所有类的混淆矩阵

微平均

将混淆矩阵的各个格子相加，再求出对应指标（例如F1-score等）

宏平均

先求出相应指标，再平均

kNN算法

K邻近算法（kNN）是一种常用的监督学习算法，其工作机制非常简单

1）给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本

2）然后基于这k个邻居的信息进行预测

3）通常在分类任务中可使用“投票法”，即选择这k个样本中出现最多的类别标记作为预测结果

4）还可以基于距离远近进行加权投票，距离越近则样本权重最大

kNN是懒惰学习（lazy learning）的著名代表，无序训练，在收到样本之后再进行处理即可

k值的选取和距离度量的选择会影响判断的结果

若k值太小，则容易受到噪声扰动

若k值太大，则可能受到较远样本的影响而预测错误

维数灾难

高维数据会给机器学习带来障碍，不仅kNN算法面临这一问题，其他机器学习方法也存在通用问题

维度太大，则样本会很稀疏，要想使样本布满空间，所需样本数不可能实现，这导致某个区域附件可能根本没有样本

位数太大时，计算距离本身都存在困难

常用的位数约束算法

多维缩放（MDS）、主成分分析（PCA）等

kNN算法的特点

不需要建立模型，训练开销为零，但预测时需要大量运算

基于局部信息进行预测，对噪声很敏感

可以生成任意姓形状的决策边界

数据预处理、选择合适的距离度量是非常重要

支持向量机（SVM）

给定训练样本集，希望在样本空间中找到一个超平面，将不同类别的样本分开

直观上看，应该找位于两类训练样本正中间的超平面，因为它对局部扰动的容忍度最好

这个超平面应该是样本距离最大的那个，称为最大边缘超平面

支持向量机的设计是针对二类问题，针对多类问题，有两种思路：

分解为K个二分类问题，针对每个类，构建分类器，区分属于这个类和不属于这个类，最后取属于某个类的概率最大者

分解为$\frac{K(K-1)}{2}$个二分类问题，每个问题都只针对两类，最后投票选择

对于其他针对二分类问题的模型，也可以采用上述思路

事实上，由于样本的随机性，可能无法找到一个完美的超平面将样本完全划分开

为解决这一问题，可以允许支持向量机在一些样本上出错，若出错则增加一个惩罚项，最后的目标是使得间隔减去惩罚之后的结果最大，这种模型称为“软间隔支持向量机”

在线性支持向量机当中，边界必须是线性的，如果实际上边界不是线性的，就需要使用非线性支持向量机

找到一个非线性变换，将样本映射，再使用线性支持向量机

困难在于这个变换函数的寻找没什么特别的道理，就是试

支持向量机的特点

数学上可转化为凸优化问题，可以找到全局最优，其他方法一般只能找到局部最优

需要决定的参数比较多，比如惩罚项系数、变换函数

朴素贝叶斯

假设各属性是相互独立的，如果各属性只能取离散值

根据训练样本，可以求出各种分类的各属性取各种值的概率

即：$P(X_i=0|Y=0)$、$P(X_i=0|Y=1)$、$P(X_i=1|Y=0)$、$P(X_i=1|Y=1)$

对于测试样本，可以根据贝叶斯公式，求出这个样本的属性下，各种分类的概率

即：$P(Y=0|X)$、$P(Y=1|X)$

选择较大者作为预测的分类

对于能取连续值的属性，假设正态分布，实际求出的是概率密度，方法类似

朴素贝叶斯的特点

对于孤立的噪声点，分类器是健壮的

面对无关性质，分类器是健壮的

若属性之间有相关关系，朴素贝叶斯的性能会降低

决策树

将整个训练样本作为根结点，重复对每个节点按照某个属性的值进行逐层划分，形成一棵树

理论上，划分的终止条件有三种：

某个节点的样本类别全部相同，无需再分

某个节点的样本属性全部相同，无法再分

某个节点不包含任何样本，不能再分

划分标准

用所有属性进行尝试，选择信息熵降低最大的那个，除此之外，还有增益率、Gini系数等划分标准

为了避免过拟合，决策树不能太复杂，可进行“剪枝”。如果划分之后，在测试集上的准确度反而还下降，就不应该进行这个划分

预剪枝

在生成树的过程中就进行剪枝

后剪枝

先生成一颗完整的树，再判断怎么剪枝

决策树的特点

对类和属性的分布不需要任何假设

构建决策树和使用决策树进行预测的效率都很高

相对容易解释

边界理论上都和坐标轴平行，不能很好适用于某些特定问题（斜决策树可克服）

对噪声的干扰具有很好健壮性

冗余属性不会造成不利影响

越分越细会导致样本越来越少（数据碎片问题），此时不应该再做分割

集成学习

构建并结合多个相对较弱的学习期来完成学习任务，通常获得比单一学习器显著优越的泛化能力

Boosting

每轮提升上一轮分类错误的样本权重，应用于决策树就是随机森林

Bagging

每次用一小部分数据，训练许多分类器再投票，应用于决策树就是GBDT

总结与归纳

无监督分类算法

聚类问题（Clustering）概述

聚类问题试图将数据集中的样本划分为若干不想交的子集，每个子集称为一个簇

训练样本的标记信息是未知的，目标是揭示数据的内在性质和规律

聚类问题的评价指标

外部指标

与某个参考模型或实际情况进行比较

Jaccard系数（JC）=$\frac{a}{a+b+c}$

FM指数（FMI）=$\sqrt{\frac{a}{a+b}\times \frac{a}{a+c}}$

Rand指数（RI）=$\frac{2(a+d)}{m(m-1)}$（其中$m=\frac{n(n-1)}{2}$）

内部指标

只考察聚类结果本身，没有信息可供参考，好的聚合结果应该组内紧密、组间分散

凝聚度SSE

各个簇内部点的距离平方的平均值

分离度SSB

各个簇质心到整体均值的距离平方和

轮廓系数（Silhouette Coefficient）=$\frac{b-a}{max(a,b)}$

$a$表示点到簇内其他点的平均距离，$b$表示点到另一个簇所有点的平均值（取最小者）

DB指数（DBI）：$max\frac{avg(C_i)+avg(C_j)}{d_{cen}(i,j)}$

$avg(C_i)$表示第$i$个簇内所有点的平均距离，$d_{cen}(i,j)$表示两个簇中心的距离

Dunn指数（DI）：$\frac{d_{min}(i,j)}{maxdiam}$

其中$d_{min}(i,j)$表示两个簇样本之间的最小距离，diam表示簇内样本的最远距离

K均值方法（K-means）

K均值方法是一种基于原型的聚类，假设聚类结构通过一组原型刻画

原型通常是质心，即簇中所有点的均值，也可以用最有代表性的点

每个对象到这个簇的原型，比到其他簇的原型更近

这种簇会趋向于圆球状

过程

随机选择K歌点作为初始质心

重复以下步骤

​ 将其余每个点指派到最近的质心，形成K个簇

​ 重新计算质心

直到质心不再发生变化

K-means++

K均值方法的初始质心如果选择不当，结果会很差，K-means++算法改进了这一步骤

先随机选择一个点

再选择下一个点，但距离越远，选到的概率越大

重复上述步骤，直至选出K个点

如果样本过多，则运算会很慢，mini-batch K均值方法每次只选取一小批样本进行运算，可以加速算法收敛，但效果会打折扣

K值选择

如何选择K值？可采用肘部法则

用不同的k进行聚类，得到SSE（或其他指标），找到下降幅度明显趋缓的点作为k的取值

优点

计算简单，可用于各种数据类型

变种（例如K-means++）克服了初始化问题的影响

缺点

只适用于球形的簇，不能处理其他形状的簇

仅限于具有中心概念的数据

离群点影响很大

K值必须事先指定

DBSCAN

DBSCAN方法是一种基于密度的聚类，簇是对象的稠密区域，被低密度的区域所包围

基于中心的密度：

核心点

位于簇内部，给定半径Eps内（邻域）的点数量超过阈值MinPts

边界点

不是核心点，但落入某个核心点的邻域内

噪声点

既不是核心点，也不是边界点

过程

判断每个点属于核心点、边界点还是噪声点

删除噪声点

连接距离小于阈值的核心，彼此相连的核心点构成一个簇

将边界点指派到关联的簇当中

参数

如何确定参数？

观察每个点到它最近的k个点的距离（k-距离），簇内的点应该较小，而噪声点应该较大

给定k，画出k-距离的累计值，如果看到急剧变化，则可以对应Eps值

二维数据集经验上取k=4比较合理

优点

基于密度的定义是相对抗噪声的

能处理任意形状和大小的簇，能发现K-means发现不了的簇

缺点

对于高维数据的密度定义困难

为了计算所有点对的距离，计算开销很大

层次聚类

层次聚类有两种主要方法：

凝聚方法

开始时每个点自己是一个簇，每一步合并两个最接近的簇，直至只剩下一个簇

这种方法需要定义簇的邻近性

分裂方法

开始时所有点构成一个簇，每一步分裂一个簇，直至每个点各成一簇

这种方法需要确定如何判断分裂哪个簇、如何分裂

注意

其中凝聚法更为常用

层次聚类常常使用树状图或嵌套族图，表示簇合并或分裂的次序

若指定要分成几个簇，事实上是指定了凝聚或分裂到哪个层级

基本凝聚层次聚类算法

预先计算邻近矩阵

每一步合并最接近的两个簇

更新邻近矩阵

重复以上步骤，直至所有点属于一个簇

邻近度

如何定义邻近度？

单链（min）

两个簇中任意两点距离的最小值，适合处理非椭圆形状的簇，但对噪声和离群点不太敏感

全链（max）

两个簇中任意两点距离的最大值，偏好球形，容易使大的簇分裂，对噪声和离群点不太敏感

组平均

两个簇中所有点对距离的平均值

Ward方法

两个簇合并时导致平方误差的增量

质心方法

两个簇的质心距离

优点

能形成层次结构

有时能产生高质量的聚类

缺点

计算开销大

一旦做出决定则不可撤销，容易陷入局部最优

谱聚类

谱聚类是从图论演化出来的算法，后来在聚类中得到广泛的应用

主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来，距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高

通过对所有数据点组成的图进行切图，让切图后不同子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的

优点

谱聚类只需要数据之间的相似度矩阵，处理稀疏数据的聚类很有效

在处理高维数据聚类时的复杂度比传统聚类算法好

缺点

若数据降维不够，谱聚类也很难得到较好结果

结果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同

总结与归纳

如何选择聚类算法？

时间序列模型

时序分析基础

时间序列数据规律

时间序列数据性质

平稳性

强平稳

数据分布在实践的平移下的分布保持不变

弱平稳

均值，方差，自相关系数等不因时间变化而变化

校验方法

直观分析法（时序图，包括均值、方差等）

数学校验法（单位根校验，ADF、KPSS）

差分

将数据转换为平稳性数据，对时间序列进行相邻观察值之间的减法操作

一阶差分是指当前时刻的观察值减去上一时刻的观察值

二阶差分是指一阶差分再减去上一刻的观察值，依次类推

自相关性

意义

时间序列中某一个时刻的值和另一个时刻的值之间的关系发现

度量方法

相关系数、自相关函数（ACF）、偏自相关函数（PACF）

度量结果

正相关性、负相关性、零相关性

截尾

是指时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶后接近或等于零或者急剧下降的性质。截尾表示时间序列的相关性在该阶之后逐渐减弱，数据不再受之前的值的影响

拖尾

即ACF或PACF并不在某阶后均为零。在某个阶数之后仍然保持较高的值，或者出现明显的周期性波动，那么这个时间序列就具有拖尾的特性。拖尾表示时间序列的相关性在该阶数之后仍然存在，存在长期的依赖关系

数据预处理

异常数据值处理

离群点

删除

缺失值

缺失值发生在时间序列的开头或者尾部，可采用直接删除的方法

缺失值发生在序列的中间位置，则采用替换缺失值的方法

替换方法

序列平均值：整个序列的平均值

临近点的平均值：相邻若干点的平均值

临近点的中位数：相邻若干点的中位数

线性插值：相邻两个点的平均值

临近点的线性趋势：回归拟合

季节性分析

前提

具备年内周期性

目的

将时间序列数据拆分成具有不同特征和规律的成分

应用

理解数据的趋势、季节性和随机波动成分，进行预测、分析和决策提供依据

常用模型算法

朴素预测法

朴素模型的思路，假定未来的需求将完全复制过去的模式。朴素模型又称为随机漫步法，有时也被称为无变化模型，因为，它预测未来时期的结果和过去观察到的实际结果完全一样，没有变化

Naive Forecast，是指预测下一期需求时，下一期的预测数量等于本期的实际需求数量
$$y_{t+1}=y_t$$

简单平均法

预测的期望值等于所有先前观察点的平均值，简称简单平均法
$$y_{t+1}=\frac{1}{n}\sum _{i=1}^n{y}_i$$

移动平均法

计算过去一段时间内的观测值的平均值来预测未来的值

简单移动平均SMA

最近的价值才重要，计算移动平均值涉及到“滑动窗口”的大小值p，根据之前数值的固定有限数p的平均值预测某个时序中的下一个值
$$y_i=\frac{1}{p}\sum _{i=l-p}^{l-1}{y}_i$$

加权移动平均WMA

滑动窗口期内的值被赋予不同的权重，通常来讲，最近时间点的值越重要
$$y_l=\frac{1}{p}\sum _{i=l-p}^{l-1}wi\cdot y_i$$

指数平均法

利用指数加权的方式对历史数据进行平滑处理，较新的数据具有更高的权重（简单平均和移动平均的集成）

指数平滑法相比更早时期内的观测值，越近的观测值会被赋予更大的权重，而时间越久的权重越小

一次指数平滑法

适用于没有明显趋势或季节性的数据。它使用加权平均来预测未来的值，其中近期的观测值具有更高的权重

二次指数平滑法

除了考虑数据的水平外，还考虑数据的线性趋势。它使用两个平滑参数，一个用于水平，另一个用于趋势

三次指数平滑法

同时考虑数据的水平和季节性模式。它使用三个平滑参数：一个用于水平，一个用于趋势，还有一个用于季节性

自回归移动平均模型ARMA

ARMA模型将自回归（AR）和移动平均（MA）两种方法结合起来，用于描述时间序列数据的动态特性

ARMA模型一般形式可以表示为ARMA(p，q)，其中$p$代表自回归阶数，$q$代表移动平均阶数

移动平均

将时间序列中的每个值与前面若干个值的平均值进行比较，用于平滑数据和检测趋势

自回归

将时间序列的当前值与其过去若干值进行线性组合，用于预测未来值
$$y_t={\alpha }_0+\sum _{i=1}^p{\alpha }_i{y}_{t-i}+{ϵ}_t+\sum _{i=1}^q{\beta }_i{ϵ}_{t-i}$$

差分自回归移动平均模型ARIMA

建立ARIMA模型一般有三个阶段，分别是模型识别和定阶、参数估计和模型检验

模型识别和定阶

确定p，d，q三个参数，差分的阶数d一般通过观察图示，1阶或2阶即可

模型校验

1）检验参数估计的显著性（t检验）

2）检验残差序列的随机性，即残差之间是独立的。残差序列的随机性可以通过自相关函数法来检验，即做残差的自相关函数图

季节性自回归移动平均模型SARIMA

SRAIMA季节性自回归移动平均模型在ARIMA模型的基础上增加了季节性的影响，结构参数有七个：SARIMA（p，d，q）（P，D，Q，s）

时序建模流程

1）数据收集

2）数据清洗和预处理：处理缺失值、异常值、平稳性检验、去除趋势和季节性等。

3）可视化和探索性数据分析（EDA）：通过绘制时间序列图、自相关图、偏自相关图等对数据进行可视化和探索性分析，以了解数据的基本特征。

4）模型选择：根据数据的特点，选择合适的时序模型，可能包括自回归模型（AR）、移动平均模型（MA）、自回归移动平均模型（ARMA）、自回归积分移动平均模型（ARIMA）等。

5）参数估计：对所选的模型进行参数估计，可以使用最大似然估计等方法来估计模型的参数。

6）模型诊断：对建立的模型进行诊断，包括残差分析、模型拟合优度检验等，以确保模型的合理性和有效性。

7）模型预测：利用建立的模型对未来的数据进行预测，可以使用模型的预测能力进行评价，并进行预测结果的解释和分析。

8）模型优化和调参：根据模型的预测效果对模型进行调优和调参，以提高模型的预测准确性。

9）结果解释和应用：

相关性分析和差异性分析

概念

相关性分析

指的是两个随机变量（或随机向量）之间的（线性）相关性，衡量两个变量之间的关联程度。

差异性分析

比较不同组别之间的差异

相关定义

连续变量

对连续的指标测量所得到的数值

二分类变量

只有两个类别的二分类变量，二分类变量的类别之间没有内在顺序

有序分类变量

两个或者多个已排序的类别

无序分类变量

具有三个及以上类别的分类变量。无序分类变量的类别之间没有内在顺序，也不能像有序分类变量类别那样进行排序

自变量

预测变量或解释变量

因变量

应答变量或结局变量

方法选择

使用相关性分析的情况

1）只想分析两个变量之间是否存在相关关系，不需要区分自变量和因变量时可用相关性分析。

2）通常在进行回归分析之前，都需要进行相关性分析。

相关性分析的方法

1）变量特性可以通过绘制散点图判断

2）通过计算显著性系数判断是否相关（主要是P值）

3）通过计算相关性系数判断相关性大小（主要是r值）

显著性系数判定方法

P值是用来进行显著性检验的，用来检验变量之间是否具有差异以及差异是否显著。

若P值>0.05代表数据之间不存在显著性差异；若P值<0.05，代表数据之间存在显著性差异。

相关系数判定方法

判定准则

一般可分为三级划分:$\left|r\right|$<0.4为低线性相关；0.4$ \leq KaTeX parse error: Can't use function '$' in math mode at position 19: …ft | r \right |$̲<0.7为显著性相关；0.7$…\left | r \right |$<1为高度线性相关。

计算方法

Pearson系数：叫皮尔逊相关系数，也叫线性相关系数，用于进行线性相关发内心，是最常用的相关系数，当数据满足正太分布时会使用该系数。

Spearman系数：当数据不满足正态分布，使用该系数。

相关性系数判定方法-Pearson相关系数

用于衡量两个连续变量之间的线性相关程度，基于协方差的概念，通过计算两个变量的协方差除以它们各自的标准层的乘积，得到一个范围在-1到1之间的相关系数。

适用范围

1）两个变量之间是线性关系，都是连续数据。

2）两个变量的总体是正态分布，或接近正态的单峰分布。

3）两个变量的观测值是成对的，每对观测值之间相互独立。

相关性系数判定方法-Spearman秩相关系数

Spearman秩相关系数的计算需要先将原始数据转换为秩次（即按大小排序后的顺序排名），然后再计算秩次之间的Pearson相关系数。用于衡量两个变量之间的单调关系，不要求变量服从正态分布

适用范围

1）两个变量的观测值是成对的等级评定资料

2）由连续变量观测资料转化得到的等级资料

选择基准

Spearman和Pearson使用选择：

1）连续数据，正态分布，线性关系，用Pearson相关系数是最恰当，当然用Spearman相关系数也可以，就是效率没有Pearson相关系数高。

2）上述任一条件不满足，就用Spearman相关系数，不能使用Pearson相关系数。

3）两个定序测量数据之间也用Spearman相关系数，不能用Pearson相关系数。

差异性分析概述

差异性分析是指两组或多组数据进行比较，以确定它们之间在某些变量上的差异或相似性的统计分析方法

常用方法

原理：比较均值/频数

目的：检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。又称[差异性显著检验]，是假设检验的一种，判断样本间差异主要是随机误差造成的，还是本质不同。

T检验

可以用于比较两组数据之间是否来自同一分别（可以用于比较两组数据的区分度）

主要用途：样本均数与总体均数的差异；两样本均数的差异比较

方差分析

用于比较三个或三个以上组别的均值是否存在显著差异的统计方法

基于组内变异和组间变异的比较来判断各组均值的差异情况。它将总体方法分解为组间变异和组内变异两部分，然后通过比较这两部分的大小来判断各组均值是否存在显著性差异

卡方分析

1）用于比较观察频数与期望频数之间的拟合优度或独立性的统计方法。

2）适用于分类变量的独立性检验和拟合优度检验

3）原理是通过比较观察频数和期望频数之间的差异来判断两个变量之间是否存在关联或拟合程度

显著性分析比较

T校验用于比较两组数据（例如，两个独立样本）的均值是否有显著差异

方差分析（ANOVA）用于比较三组或更多组数据的均值是否有显著差异。它通常用于检验一个或多个独立变量对一个因变量的影响

卡方分析用于检验两个分类变量是否独立。它属于观察频数与期望频数之间的差异来工作，通常用于检验分类数据之间的关联性

每个检验都返一个p值，这个p值可以用来判断观察到的差异是否可能是由随机误差引起的，还是确定存在显著性差异。通常，如果p值小于某个预定的显著性水平（例如0.05），我们就拒绝原假设（即认为数据之间不存在显著性差异的假设），并认为观察到的差异是不显著的。

机器学习模型

机器学习

通过算法使得机器能从大量数据中学习规律从而对新的样本做决策。数据和特征决定了机器学习结果的上限，而模型算法只是尽可能逼近这个上限。

流程：原始数据->数据预处理->特征提取->特征转换->预测->结果

深度学习

通过构建具有一定“深度”的模型，可以让模型来自动学习好的特征表示（从底层特征，到中层特征，再到高层特征），从而最终提升预测或识别的准确性。

流程：原始数据->中层特征->高层特征->预测->结果

神经网络

人工神经网络主要由大量的神经元以及它们之间的有向链接构成。因此考虑三方面：

1）神经元的激活规则：主要是指神经元输入到输出之间的映射关系，一般为非线性函数

2）网络的拓扑结构：不同神经元之间的连接关系

3）学习算法：通过训练数据来学习神经网络的参数

激活函数

激活函数对输入信息进行非线性变换。然后将变换后的输入信息作为信息传给下一层神经元

1）Sigmoid函数：数据被变换在0和1之间，对于特别小的负数输出为0，特别大的正数输出为1

2）Tanh函数：将元素的值变换到-1和1之间，形状和Sigmoid函数的形状很像，但tanh函数在坐标系的原点上对称

3）ReLu函数：ReLu函数只保留正数元素，并将负数元素清零

Softmax函数：用于多分类问题的激活函数，对于长度为K的任意实向量，Softmax可以将其压缩为长度为K，值在（0,1）范围内，并且向量中元素的总和为1的实向量

注意：ReLu函数是一个通用的激活函数，目前大多数情况下使用。但是ReLu函数只能在隐藏层中使用；用于分类器时，Sigmoid函数及其组合效果更好，由于梯度消失问题，有时要避免使用Sigmoid和Tanh函数’在神经网络层数较多时候，最好使用ReLu函数，ReLu函数比较简单计算量少，而Sigmoid和Tanh函数计算量大很多；在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。

神经网络

人工神经网络由神经元模型构成，大体上分为三种类型，但是大多数网络都是复合型结构，即一个神经网络中包括多种网络结构

层：一组神经网络中负责处理一组输入特征或一组神经元的输出的神经元

全连接层：又称密集层，一种每个节点均与下一隐藏层中每个节点相连的隐藏层

输入层：神经网络的第一层

输出层：神经网络的最后一层

损失函数

在深度学习中，损失函数（loss）起着至关重要的作用。它用于衡量模型预测与真实值之间的差异，通过优化算法指导模型的训练过程。

1）绝对损失（MAE）：它计算的是预测值与真实值之间绝对值的平均值，对损失函数在处理回归问题时较为常用

2）平方损失（MSE）：它计算的是预测值与真实值之间平方的平均值，平方损失函数在处理回归问题时也常被使用

3）交叉熵损失：它用于解决分类问题，计算的是预测概率与真实标签之间的交叉熵值，适用于多分类问题

优化器

优化器是在深度学习反向传播过程中，指引损失函数（目标函数）的各个参数往正确的方向更新合适的大小，使得更新后的各个参数让损失函数（目标函数）值不断逼近全局最小

1）首先是优化方向，决定“前进的方向是否正确”，在优化器中反映为梯度或动量

2）其次是步长，决定“每一步迈多远”，在优化器中反映为学习率

分类：

随机梯度下降（SGD）：每次从训练集中随机选择一个样本来进行学习

SGDM（加入一阶动量）：一阶动量是各个时刻梯度方向的指数移动平均值，也就是说，t时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定

AdaGrad（加入二阶动量）：用下一个点的梯度方向，与历史累计动量相结合

RMSOrop：梯度平方和累加为指数加权的移动平均，使得其在非凸设定下效果更好

Adam：Adam结合了前面的方法的一阶动量和二阶动量

选择优化器要考虑的因素

数据集的规模和复杂性

对于大规模数据集和复杂模型，应该选择具有较好收敛性的优化器，如SGD和Adam

模型的稀疏性

对于稀疏模型，应该选择Adagrad或其他自适应学习率的优化器

训练模型

对于需要较快训练速度的场景，可以选择具有加速功能的优化器，如SGD的带动量更新或Nesterov动量更新，或者选择具有较高并行性的优化器，如Adam或Adagrad

学习率的调整

对于需要调整学习率的场景，可以选择自适应学习率的优化器，如Adam或Adagrad

算法选择路径图

回归模型

回归方法是一种对数值型连续随机变量进行预测和建模的监督学习算法

使用案例一般包括房价预测、股票走势或测试成绩等连续变化的案例

特点是标注的数据集具有数值型的目标变量，每个观察样本都有一个数值型的标注真值以监督算法回归模型

常见的回归模型

线性回归（超平面拟合）

岭回归

决策树回归

最近邻算法knn（搜寻最相似的训练样本来预测观察样本的值）

Lasso回归（最小绝对值收敛和选择算子算法）

深度学习

岭回归

岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法。岭回归主要解决的问题是两种：一是当预测变量的数量超过观测变量的数量时候（预测变量相当于特征，观测变量相当于标签），二是数据集之间具有多重共线性，即预测变量之间具有相关性

防止过拟合

自变量X至少一项或以上的定量变量或二分类定类变量

因变量Y要求为定量变量（若为定类变量，请使用逻辑回归）

Lasso回归

Lasso回归是一种数据挖掘方法，即在常用的多元线性回归中，添加惩罚函数，不断压缩系数，从而达到精简模型的目的，以避免共线性和过拟合。当系数为0时，同时达到筛选变量的效果

决策树回归

在面对不同数据时，决策树也可以分为两大类型：分类决策树和回归决策树。前者主要用于处理离散型数据，后者主要用于处理连续性数据。采用的是启发式的方法。假如我们有n个特征，每个特征有$S_i$个取值，那我们遍历所有特征，尝试该特征的所有取值，对空间进行划分，直到取到特征$j$的取值$s$，使得损失函数最小，这样就得到一个划分点

分类模型

分类模型是一种对离散型随机变量建模或预测的监督学习算法

使用案例包括邮件过滤、金融欺诈和预测雇员异动等输出为类别的任务

分类算法通常适用于预测一个类别（或类别的概率）而不是连续的数值

分类模型

逻辑回归（logistic函数（即Sigmoid函数）将预测映射到0到1中间）

分类树（决策树、随机森林）

深度学习

支持向量机SVM（核函数、超平面）

朴素贝叶斯（基于贝叶斯定理和特征条件独立假设、概率）

聚类模型

聚类是一种无监督学习任务，该算法基于数据内部结构寻找观察样本的自然族群（即集群）

使用案例包括细分客户、新闻聚类、文章推荐等

无监督学习（即数据没有标注），并且通过使用数据可视化评价结果

聚类模型

K-means聚类（聚类的度量基于样本点之间的几何距离）

层次聚类（自顶向下、自底向上）

谱聚类（图、子图）

DBSCAN（基于密度的算法，它将样本点的密集区域组成一个集群）

降维模型

降维就是对高维度特征数据预处理方法。降维是将高维数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的

降维模型

PCA（主成分分析）

自编码器AE

PCA

PCA的主要目的是为了得到方差最大的前N个特征，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大（即方差最大）的$k$个特征所对应的特征向量组成的矩阵。这样就可以将数据转换到新的空间当中，实现数据特征的降维[线性降维]

流程图

自编码器

自编码器通过无监督学习的方式，将输入数据压缩成低维表示，再从低维表示中重构出原始数据。编码器将输入数据压缩成低维表示，而解码器则尝试从压缩后的表示中重构出原始数据。通常比较重构数据和原始数据的差异来实现，例如均方误差（MSE）或交叉熵等

深度学习

optimizer：优化器，用于控制梯度裁剪。必选项

loss：损失函数（或称目标函数、优化评分函数）。必选项

metrics：评价函数用于评估当前训练模型的性能。当模型编译后（compile），评价函数应该作为metrics的参数来输入。评价函数和损失函数相似，只不过评价函数的结果不会用于训练过程中

批次（batch）：模型训练的一次迭代（一次梯度更新）中使用的样本集

批次大小（batch size）：一个批次中的样本数

轮次（epoch）：在训练时，整个数据集的一次完整的遍历

卷积神经网络CNN

卷积神经网络属于神经网络的一个重要分支。应用于CV，NLP等的各个方面。CNN通过使用卷积层、池化层和全连接层来提取出图像中的局部特征

1）卷积层通过滤波器对图像进行卷积操作，提取出图像中的局部特征

2）池化层不改变三维矩阵的深度，可以缩小矩阵的大小，进一步缩小最后全连接层中节点的个数，从而到达减少整个神经网络的目的

3）全连接层（FC）在整个卷积中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间，全连接层则起到将学到的“分布式特征映射”到样本标记空间的作用

循环神经网络RNN

循环神经网络，是指在全连接神经网络的基础上增加了前后时序上的关系，可以更好地处理比如机器翻译等的与时序相关的问题。RNN的目的就是用来处理序列数据的。

1）x是一个向量，它表示输入层的值；

2）s是一个向量，它表示隐藏层的值

3）U是输入层到隐藏层的权重矩阵

4）O也是一个向量，它表示输出层的值

5）V是隐藏层到输入层的权重矩阵

6）循环神经网络的隐藏层的值S不仅仅取决于当前这次的输入x还取决于上一次隐藏层的值s。权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重。

长短期记忆LSTM

长短期记忆是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。记忆单元的关键是门。这些也是加权函数，它们进一步控制单元中的信息。有3个门“

1）遗忘门。决定什么样的信息需要从单元中丢弃

2）输入门。决定输入中哪些值来更新记忆状态

3）输出门。根据输入和单元的内存决定输出什么

机理分析类

微分方程

马尔萨斯人口模型

1789年，英国神父Malthus在分析了一百多年人口统计资料后，提出Malthus模型。

模型假设：

1）$x(t)$表示t时刻的人口数，且$x(t)$连续可微

2）人口的增长率$r$是常数（增长率=出生率-死亡率）

3）人口数量的变化是封闭的，即人口数量的增加与减少只取决于人口中个体的生育和死亡，且每一个个体都具有同样的生育能力与死亡率

阻滞增长模型

如果对增长率$r$进行修正呢？我们知道，地球上的资源是有限的，它只能提供一定数量的生命生存所需的条件。随着人口数量的增加，自然资源环境条件等对人口再增长的限制作用将越来越显著。如果在人口较少时可以把增长率r看成常数，那么当人口增加到一定数量之后，就应当视$r$为一个随着人口的增加而减小的量，即将增长率$r$表示为人口$r(x)$，且$r(x)$为$x$的减函数。

模型假设：

1）设$r(x)$为$x$的线性函数，$r(x)=r-sx$（工程师原则，首先用线性）

2）自然资源与环境条件所能容纳的最大人口数为$x_m$。即当$x=x_m$时，增长率$r(x_m)=0$

Volterra模型（沃尔泰拉模型）

食饵（即猎物）和捕食者在时刻$t$的数量分别记作$x_1(t)$和$x_2(t)$。因为大海中资源丰富，可以假设如果出食饵独立生存则将以增长率$r_1$按指数规律增长，即有$\frac{d{x}_1}{dt}=r_1{x}_1$，捕食者的存在使得食饵的增长率降低，假设降低的程度正比于捕食者的数量，于是$x_1(t)$满足方程：
$$\frac{d{x}_1}{dt}=x_1(r_1-{\lambda }_1{x}_2)$$
其中：比例系数${\lambda }_1$反应捕食者掠取食饵的能力

捕食者离开食饵无法生存，若假设它独自存在时的死亡率为$r_2$，即食饵为它提供食物的作用相当于使其死亡率降低。假设这个作用与食饵数量成正比，于是$x_2(t)$满足方程：
$$\frac{d{x}_2}{dt}=x_2(-r_2+{\lambda }_2{x}_1)$$
其中：比例系数${\lambda }_2$反映食饵对捕食者的供养能力

方程（1）、（2）是在没有人工捕获情况下的自然环境中食饵与捕食者之间的制约关系，是数学家Volterra提出的最简单的模型。

考虑到人工捕获时，假设表示捕获能力或强度的系数为$e$，那么相当于食饵的自然增长率由$r_1$降为$r_1-e$，捕食者的死亡率由$r_2$增为$r_2+e$。方程变为：
{ d x 1 d t = x 1 [ ( r 1 − e ) − λ 1 x 2 ] d x 2 d t = x 2 [ − ( r 2 + e ) + λ 2 x 1 ]

$$\begin{cases} \frac{dx_1}{dt} = x_1 [(r_1 - e) - \lambda_1 x_2] \\ \frac{dx_2}{dt} = x_2 [-(r_2 + e) + \lambda_2 x_1] \end{cases}$$ {dtdx1​​=x1​[(r1​−e)−λ1​x2​]dtdx2​​=x2​[−(r2​+e)+λ2​x1​]​

种群相互竞争模型

如果一个自然环境中存在两个或两个以上的种群，它们之间的关系大致可分为以下几种：相互竞争，相互依存，弱肉强食（食饵与捕食者），也可能毫无关系。弱肉强食我们已经研究过，最后一种情形我们不用研究。所以还剩下两种关系，这部分我们先来研究两个种群的相互竞争模型，在下个部分我们再来研究两个种群的相互依存模型。

考虑单个种群在自然资源有限的环境下生存时，我们常用阻滞增长模型来描述它的数量的演变，即：$\frac{dx(t)}{dt}=rx\left(1-\frac{x}{N}\right)$,

其中$r$是增长率，$N$是该环境下能容纳的最大数量。

传染病模型

历史上曾经爆发过多次大范围的传染病，例如天花、流感、SARA、猪流感等。 2020年上半年爆发的新冠肺炎具有发病急、传播快、病情重等特点，给人们的健康 带来极大的危害，对社会的繁荣安定带来严重影响。因此，搞清楚传染病的传播过 程、分析其传播特征、传播规律，以便避免传染病的暴发、控制传染病的蔓延、最 终消灭传染病是一件非常重要的事。我们可以建立数学模型描述传染病的传播过程、 分析其传播规律、为预测和控制传染病提供信息和支持。要深入区分不同传染病的 不同传播特点，需要很多病理学知识。这里我们仅从传染病的一般传播机理出发建 立几种最常用的传染病模型。

(1)易感者(S,Susceptible):潜在的可感染人群；

(2)潜伏者(E,Exposed):已被传染但没表现出来的人群；

(3)感染者(I,Infected):确诊感染的人；

(4)康复者(R,Recovered):已痊愈的感染者，体内含抗体。 注意：以上分类的命名不唯一，例如有的文献将R解释为移出状态(removed),表 示脱离系统不再受到传染病影响的人(痊愈、死亡或被有效隔离的人)。

首先考虑最基本的模型——SI 模型。这里S 是指易感染者(Susceptible) 也就是健 康人，I指已感染者(Infective) 也就是患者。在该模型中我们把人群分为易感染者 和已感染者两大类(即健康人和患者)。

假设我们不考虑人口的迁移和生死，设总人数为$N$，那么在任意时刻$N=S+1$。接下来我们需要考虑传染病的传播机理，这里有两种不同的角度：

1）假设单位时间内，易感染者与已感染者接触且被传染的强度为$\beta$，且单位时间内，由易感染者$S$转换为已感染者$I$的人数：

$\beta \frac{S}{N}\times \frac{I}{N}\times N=\beta \frac{SI}{N}$。那么有$S(t+\Delta t)-S(t)=-\beta \frac{S(t)\times I(t)}{N}\Delta t$，$I(t+\Delta t)-I(t)=\beta \frac{S(t)\times I(t)}{N}\Delta t$。这里我们可以借用高数的知识：

$\frac{S(t+\Delta t)-S(t)}{\Delta t}=-\beta \frac{S(t)\times I(t)}{N}$，则${\lim }_{\Delta t\to 0}\frac{S(t+\Delta t)-S(t)}{\Delta t}=-\beta \frac{S\times I}{N}$，

接下来我们即可得到对应的微分方程为：
{ d S d t = − β S × I N d I d t = β S × I N

$$\begin{cases} \frac{dS}{dt} = -\beta \frac{S \times I}{N} \\ \frac{dI}{dt} = \beta \frac{S \times I}{N} \end{cases}$$ {dtdS​=−βNS×I​dtdI​=βNS×I​​
状态转移图

对于SI模型的扩展

1）考虑某种使得参数$\beta$降低的因素（例如禁止大规模聚会、采取隔离措施等）

2）增加人口自然出生率和死亡率，但不考虑疾病的死亡率。假定初始总人口数为$N=(S+I)$，疾病流行期间，人口出生率和自然死亡率分别为$\mu$和$v$，不考虑因病死亡，新增人都是易感染者，初始时单位时间内感染人数为$\beta \frac{SI}{N}$。

注意，由于总人数$N$不再固定，因此我们在后期不断对总人口$N$进行更新，新的总人口$N^{\prime }$的计算公式仍为$S+I$。其状态转移图形为：

对应的微分方程组为：
{ d S d t = − β S × I N ′ + u N ′ − ν S d I d t = β S × I N ′ − ν I , 且    N ′ = S + I d N D d t = ν S + ν I

$$\begin{cases} \frac{dS}{dt} = -\beta \frac{S \times I}{N'} + uN' - \nu S \\ \frac{dI}{dt} = \beta \frac{S \times I}{N'} - \nu I, \quad \text{且} \; N' = S + I \\ \frac{dND}{dt} = \nu S + \nu I \end{cases}$$ ⎩ ⎨ ⎧​dtdS​=−βN′S×I​+uN′−νSdtdI​=βN′S×I​−νI,且N′=S+IdtdND​=νS+νI​
3）不考虑人口自然出生率和死亡率，只考虑疾病的死亡率假定因病的死亡率为$d$，不考虑人口自然出生率和死亡率。其状态转移图形为：

对应的微分方程组为： { d S d t = − β S × I N ′ d I d t = β S × I N ′ − d I , 且    N ′ = S + I d I D d t = d I 对应的微分方程组为：

$$\begin{cases} \frac{dS}{dt} = -\beta \frac{S \times I}{N'} \\ \frac{dI}{dt} = \beta \frac{S \times I}{N'} - dI , \quad \text{且} \; N' = S + I \\ \frac{dID}{dt} = dI \end{cases}$$ 对应的微分方程组为：⎩ ⎨ ⎧​dtdS​=−βN′S×I​dtdI​=βN′S×I​−dI,且N′=S+IdtdID​=dI​
4）同时考虑人口自然出生率和死亡率和疾病的死亡率疾病流行期间，人口出生率和自然死亡率分别为$\mu$和$v$，因病的死亡率为$d$，其状态转移图形为：

对应的微分方程组为： { d S d t = − β S × I N ′ + u N ′ − ν S d I d t = β S × I N ′ − d I − ν I , 且    N ′ = S + I d I D d t = d I d N D d t = ν S + ν I 对应的微分方程组为：

$$\begin{cases} \frac{dS}{dt} = -\beta \frac{S \times I}{N'} + uN' - \nu S \\ \frac{dI}{dt} = \beta \frac{S \times I}{N'} - dI - \nu I , \quad \text{且} \; N' = S + I \\ \frac{dID}{dt} = dI \\ \frac{dND}{dt} = \nu S + \nu I \end{cases}$$ 对应的微分方程组为：⎩ ⎨ ⎧​dtdS​=−βN′S×I​+uN′−νSdtdI​=βN′S×I​−dI−νI,且N′=S+IdtdID​=dIdtdND​=νS+νI​
某些疾病容易被治愈，但是却容易发生变异，例如流感病毒。
假设从某种疾病恢复后仍不能产生抗体，即未来仍可能患病，即我们可能会经历：感染，恢复为易感者，再感染，不断循环下去的过程。
我们可以建立SIS模型来描述这一过程，假定总人口数为$N$,且不考虑因病死亡和自然出生死亡，单位时间内感染人数为$\beta \frac{SI}{N}$,由感染状态$I$恢复为易感者状态$S$的恢复率为$a$.其状态转移图形为:

对应的微分方程组为： { d S d t = α I − β S × I N d I d t = β S × I N − α I 对应的微分方程组为：

$$\begin{cases} \frac{dS}{dt} = \alpha I - \beta \frac{S \times I}{N} \\ \frac{dI}{dt} = \beta \frac{S \times I}{N} - \alpha I \end{cases}$$ 对应的微分方程组为：{dtdS​=αI−βNS×I​dtdI​=βNS×I​−αI​

数值求解类

元胞自动机

元胞自动机的定义

元胞自动机（CA）是一种应用比较广泛的模型理论，由冯·诺依曼创始，经数学家Conway、物理学家Wolfram等人的贡献后迅速发展。在物理学定义上，元胞自动机指的是，定义在一个由具有离散、有限状态的元胞组成的元胞空间上，按照一定的局部规则，在离散的时间维度上演化的动力学系统。在数学定义上，从不同的角度有着基于集合论的定义和拓扑学的定义，简单起见，在此不做阐述。

元胞自动机（CA）是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空烟花过程的能力。

元胞自动机的组成

元胞：又称细胞、单元或者基元，是元胞自动机最基本的组成部分。元胞分布在离散的欧几里得空间位置上，每个时刻有着离散的状态，如{0,1}等。

元胞空间：元胞所分布在欧几里得空间上的网格点的集合。最常见的为二维元胞空间，通常可按三角形、四边形和六边形三种网格排列。

邻居：元胞自动机的演化规则是局部的，对于指定元胞的状态进行更新时只需要知道其临近元胞的状态。某一元胞状态更新时要搜索的空间域叫做该元胞的邻居。

邻居的划分：在四方网格划分下的二维元胞自动机的邻居通常有以下几种形式：

Von Neuman型

Moore型

expend Moore型

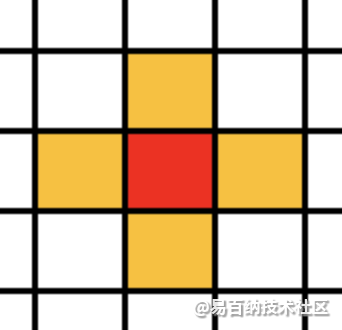
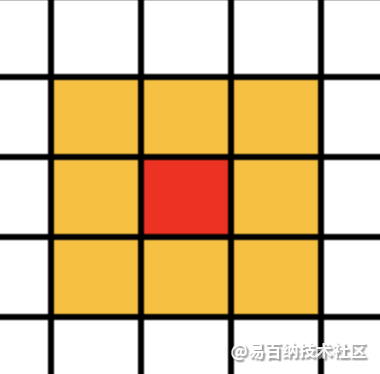
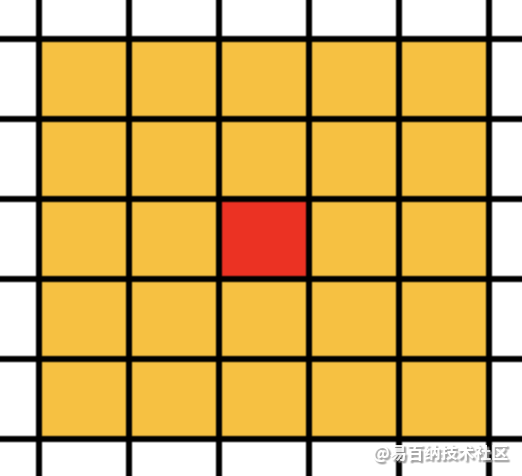
边界条件

实际模拟元胞自动机的演化时不可能处理无限网络，系统必须是有边界的。处理边界格点时，可以为边界的信息进行编码，由此选择不同的演化规则。另一种方法是在边界处扩展，以满足边界有与内部类似的邻居。

周期型边界

周期型是指相对边界连接起来的元胞空间。这种空间与无限空间最为接近，进行理论探讨时，常以此类空间作为实验进行模拟。

固定边界

所有边界外元胞均取某一固定常量。

绝热边界

边界外元胞的状态始终和边界元胞的状态保持一致。

演化规则

根据元胞当前状态及其邻居状态确定下一时刻该元胞状态的动力学函数。

元胞自动机的特征

标准的元胞自动机具有以下几个特征：

（1）同质性、齐性：同质性反映在元胞空间内的每个元胞都服从相同的规则；齐性指的是元胞的分布方式相同，大小形状相同，空间分布整齐。

（2）空间离散：元胞分布在按一定规则划分的离散的元胞空间上。

（3）时间离散：系统的演化是按等时间间隔分步进行的。$t$时刻的状态只对$t+1$时刻的状态产生影响。

（4）状态离散、有限：元胞自动机的状态参量只能取有限个离散值。

（5）同步计算（并行性）：元胞自动机的处理是同步进行的。

（6）时空局域性：每个元胞在$t+1$时刻的状态，取决于其邻居的元胞在t时刻的状态。

（7）维数高：动力系统中一般将变量的个数成为维数。任何完备元胞自动机的元胞空间是在空间上的无穷集，每个元胞的状态是这个动力学系统的变量，因此元胞自动机是一类无穷维动力系统。

应用

通过简单的规则展示了复杂系统的动态行为和模式生成能力。

常见应用领域

1.流体动力学模拟

2.交通流模拟

3.城市发展与土地利用模型

4.生物进化模拟

5.生态系统和种群动态模拟

6.火灾传播模型

7.传染病传播模拟

牛顿-拉夫逊算法（NRBO）

牛顿-拉夫逊优化算法(Newton-Raphson-based optimizer, NBRO)是一种新型的元启发式算法（智能优化算法），该成果由Sowmya等人于2024年2月发表在中科院2区Top SCI期刊《Engineering Applications of Artificial Intelligence》上。

注意：如果使用该算法记得引用该论文

原理简介

所提出的NRBO通过使用几个向量集和两个算子（如NRSR和TAO）来探索搜索域，应用NRM来发现搜索区域，从而定义搜索路径。

种群初始化

与其他元启发式算法一样，NRBO通过在候选解的边界内产生初始随机种群来启动对最优解的搜索。基于存在Np个种群的事实，并且每个种群由模糊决策变量/向量组成。因此，使用公式(7)生成随机种群：
$$x_j^n=lb+rand\times (ub-lb),n=1,2,\dots ,N_p,\text{and}j=1,2,\dots ,dim$$
其中$x_{ij}$表示第$n$个总体的第j个维度的位置，rand表示(0,1)之间的随机数。公式(8)给出了可以描绘所有维度的种群的种群矩阵：
X n = [ x 1 1 x 1 2 ⋯ x 1 d i m x 2 1 x 2 2 ⋯ x 2 d i m ⋮ ⋮ ⋱ ⋮ x N p 1 x N p 2 ⋯ x N p d i m ] N p × d i m

$$\begin{equation} X_{n} = \begin{bmatrix} x_{1}^{1} & x_{1}^{2} & \cdots & x_{1}^{dim} \\ x_{2}^{1} & x_{2}^{2} & \cdots & x_{2}^{dim} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N_{p}}^{1} & x_{N_{p}}^{2} & \cdots & x_{N_{p}}^{dim} \end{bmatrix}_{N_{p} \times dim} \end{equation}$$ Xn​= ​x11​x21​⋮xNp​1​​x12​x22​⋮xNp​2​​⋯⋯⋱⋯​x1dim​x2dim​⋮xNp​dim​​ ​Np​×dim​​​

Newton-Raphson搜索规则（NRSR）

矢量由NRSR控制，允许种群更准确地探索可行区域并获得更好的位置。NRSR是基于NRM的概念，即提出NRM是为了促进勘探趋势并加快收敛。由于许多优化技术是不可微的，因此在这种情况下，使用数学NRM来代替函数的显式公式。NRM从一个假定的初始解开始，并沿着一个确定的方向前进到下一个位置。为了从中公式(5)中获取NRSR，必须使用TS来确定二阶导数。$f(x-\Delta x)$和$f(x+\Delta x)$的TS如下所示：
f ( x + Δ x ) = f ( x ) + f ′ ( x 0 ) Δ x + 1 2 ! f ′ ′ ( x 0 ) Δ x 2 + 1 3 ! f ′ ′ ′ ( x 0 ) Δ x 3 + ⋯ f ( x − Δ x ) = f ( x ) − f ′ ( x 0 ) Δ x + 1 2 ! f ′ ′ ( x 0 ) Δ x 2 − 1 3 ! f ′ ′ ′ ( x 0 ) Δ x 3 + ⋯

$$\begin{align} f(x+\Delta x) &= f(x) + f'(x_0)\Delta x + \frac{1}{2!}f''(x_0)\Delta x^2 + \frac{1}{3!}f'''(x_0)\Delta x^3 + \cdots \\ f(x-\Delta x) &= f(x) - f'(x_0)\Delta x + \frac{1}{2!}f''(x_0)\Delta x^2 - \frac{1}{3!}f'''(x_0)\Delta x^3 + \cdots \end{align}$$ f(x+Δx)f(x−Δx)​=f(x)+f′(x0​)Δx+2!1​f′′(x0​)Δx2+3!1​f′′′(x0​)Δx3+⋯=f(x)−f′(x0​)Δx+2!1​f′′(x0​)Δx2−3!1​f′′′(x0​)Δx3+⋯​​
通过减去/加上公式(9)和公式(10)，得出$$f^{\prime }(x)$$和$f^{\prime }(x)$的表达式如下：
$$\begin{array}{rl}{f}^{\prime }(x)& =\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}\\ f^{\prime \prime }(x)& =\frac{f(x+\Delta x)+f(x-\Delta x)-2f(x)}{\Delta x^2}\end{array}$$
代入公式(5)中的公式(11)和公式(12)，更新的根位置被重写如下：
$$\begin{array}{c}{x}_{n+1}=x_n-\frac{(f(x_n+\Delta x)-f(x_n-\Delta x))\times \Delta x}{2\times (f(x_n+\Delta x)+f(x_n-\Delta x)-2\times f(x_n))}\end{array}$$
考虑到NRSR应该是NRBO的主要组成部分，有必要进行某些调整，以管理种群搜索作为公式(13)的结果。彼此相邻的x的位置分别用$x_n+\Delta x$和$x_n-\Delta x$表示，如图2所示。NRBO将这对相邻位置转换为种群中的另外两个向量。因为$f(x_n)$是一个最小化问题，如图2所示。位置$x_n+\Delta x$的适应度值比位置$x$差，而位置$x_n-\Delta x$的适合度比位置$x_n$大。因此，NRBO替换位置$X_b$的位置$x_n-\Delta x$，位置$X_b$在其邻域中具有比位置$x_n$更好的位置，而位置$x_n+\Delta x$被$X_w$的位置替换，位置$X_w$在其邻域内具有比位置$x_n$更差的位置。这个方法的另一个优点是，它使用位置$x_n$而不是其适应度$f(x_n)$，这节省了计算时间。因此，NRSR表示如下：
$$\begin{array}{c}\text{NRSR}=\text{randn}\times \frac{(X_w-X_b)\times \Delta x}{2\times (X_w+X_b-2\times x_n)}\end{array}$$
其中randn表示均值为0、方差为1的正态分布随机数，$X_w$表示最差位置，$X_b$表示最佳位置。等式（14）可以通过用当前解决方案来辅助更新其位置来增强当前解决方案。等式（14）具有随机参数，以增加NRBO的搜索能力并更好地平衡开发和探索能力。

根据经验，所提出的算法必须能够在多样性和聚集性之间达到平衡，以便在搜索空间中发现最优解，并最终收敛到全局解。可以通过应用一个称为$\delta$的自适应系数来增强算法。$\delta$的表达式如公式(15)所示：
$$\delta ={\left(1-\left(\frac{2\times IT}{Max\_IT}\right)\right)}^5$$
其中$IT$表示当前迭代，而$MaxIT$表示迭代的最大次数。为了在勘探和开发阶段之间保持平衡，参数$\delta$在迭代过程中会自行调整。图3说明了每次迭代过程中$\delta$的变化。根据公式(15)，$\delta$的值在1到−1之间变化。

与自适应参数$\delta$一起，所提出的NRSR通过考虑优化过程中的随机动作、增加多样性和避免局部最优来改进NRBO，同时显著减少迭代次数。公式(14)中$\Delta x$的表达式如公式(16)所示：
$$\Delta x=rand(1,dim)\times \left|X_b-X_n^{IT}\right|$$
其中$X_b$表示迄今为止获得的最佳解，rand(1,dim)是具有dim维度决策变量的随机数。现在，通过考虑NRSR来修改公式(13)，并重写如下：
$$x_{n+1}=x_n-NRSR$$
接着，通过包括另一个称为$\rho$的参数来改进所提出的NRBO的利用，该参数将种群引导到正确的方向。ρ的表达式如下所示。
$$\rho =a\times \left(X_b-X_n^{IT}\right)+b\times \left(X_{r_1}^{IT}-X_{r_2}^{IT}\right)$$
其中$a$和$b$是(0,1)之间的随机数，$r_1$和$r_2$是从总体中随机选择的不同整数。然而，$r_1$和$r_2$的值不相等。矢量的当前位置$X_n^{IT}$已经由公式(19)更新：
$$X_n^{IT}=x_n^{IT}-\left(randn\times \frac{(X_w-X_b)\times \Delta x}{2\times (X_w+X_b-2\times X_n)}\right)+\left(a\times (X_b-X_n^{IT})\right)+b\times \left(X_{r_1}^{IT}-X_{r_2}^{IT}\right)$$
其中$X{1}_n^{IT}$是通过更新$x_n^{IT}$而得到的新矢量位置。NRSR是由NRM进一步改进，并且公式(13)被修改和重写如下：
NRSR = r a n d n × ( y w − y b ) × Δ x 2 × ( y w + y b − 2 × x n ) y w = r 1 × ( Mean ⁡ ( Z n + 1 + x n ) + r 1 × Δ x ) y b = r 1 × ( Mean ⁡ ( Z n + 1 + x n ) − r 1 × Δ x ) Z n + 1 = x n − r a n d n × ( X w − X b ) × Δ x 2 × ( X w + X b − 2 × x n )

$$\begin{align} \text{NRSR} &= randn \times \frac{(y_w - y_b) \times \Delta x}{2 \times (y_w + y_b - 2 \times x_n)} \\ y_w &= r_1 \times \left( \operatorname{Mean}(Z_{n+1} + x_n) + r_1 \times \Delta x \right) \\ y_b &= r_1 \times \left( \operatorname{Mean}(Z_{n+1} + x_n) - r_1 \times \Delta x \right) \\ Z_{n+1} &= x_n - randn \times \frac{(X_w - X_b) \times \Delta x}{2 \times (X_w + X_b - 2 \times x_n)} \end{align}$$ NRSRyw​yb​Zn+1​​=randn×2×(yw​+yb​−2×xn​)(yw​−yb​)×Δx​=r1​×(Mean(Zn+1​+xn​)+r1​×Δx)=r1​×(Mean(Zn+1​+xn​)−r1​×Δx)=xn​−randn×2×(Xw​+Xb​−2×xn​)(Xw​−Xb​)×Δx​​​
其中$y_w$和$y_b$是使用$Z_{n+1}$和$x_n$生成的两个向量的位置，$r_1$表示(0,1)之间的随机数。NRSR的增强版本如公式(20)所示。使用公式(20)之后，公式(19)被更新如下：
$$\begin{array}{c}{X}_n^{IT}=x_n^{IT}-\left(randn\times \frac{(y_w-y_b)\times \Delta x}{2\times (y_w+y_b-2\times x_n)}\right)+\left(a\times (X_b-X_n^{IT})\right)+b\times \left(X_{r_1}^{IT}-X_{r_2}^{IT}\right)\end{array}$$
有必要通过用等公式(24)中的当前矢量$x_n^{IT}$的位置代替最佳矢量$X_b$的位置来构造新矢量$X{2}_n^{IT}$：
$$\begin{array}{c}X{2}_n^{IT}=X_b-\left(randn\times \frac{(y_w-y_b)\times \Delta x}{2\times (y_w+y_b-2\times x_n)}\right)+\left(a\times (X_b-X_n^{IT})\right)+b\times \left(X_{r_1}^{IT}-X_{r_2}^{IT}\right)\end{array}$$
开发阶段是这一搜索方向策略的主要重点。当涉及到局部搜索时，公式(25)提出的搜索方法是有益的，但当涉及到全局搜索时它有局限性；而公式(24)给出的搜索策略对于全局搜索是有益的，但对于局部搜索有局限性。因此，NRBO同时使用公式(24)和(25)来改善多样化和强化阶段。下一次迭代期间的新位置矢量用公式(26)、(27)表示：
$$\begin{array}{rl}{x}_n^{IT+1}& =r_2\times \left(r_2\times X{1}_n^{IT}+(1-r_2)\times X{2}_n^{IT}\right)+(1-r_2)\times X{3}_n^{IT}\\ X{3}_n^{IT}& =X_n^{IT}-\delta \times \left(X{2}_n^{IT}-X{1}_n^{IT}\right)\end{array}$$
其中$r_2$表示(0,1)之间的随机数。

陷阱规避操作（TAO）

纳入TAO是为了提高建议的NRBO处理现实世界问题的有效性。TAO是采用Ahmadianfar等人提出的改进和增强运算公式。使用TAO可以显著改变$x_n^{IT+1}$的位置。它通过组合最佳位置$X_b$和当前矢量位置$X_n^{IT}$来产生具有增强质量XITTAO的解决方案。如果rand的值小于$DF$，则使用如下公式产生解XITTAO：
X T A O I T = { X n I T + 1 + θ 1 × ( μ 1 × x b − μ 2 × X n I T ) + θ 2 × δ × ( μ 1 × Mean ⁡ ( X I T ) − μ 2 × X n I T ) , if  μ 1 < 0.5 x b + θ 1 × ( μ 1 × x b − μ 2 × X n I T ) + θ 2 × δ × ( μ 1 × Mean ⁡ ( X I T ) − μ 2 × X n I T ) , Otherwise

$$\begin{equation} X_{TAO}^{IT} = \begin{cases} X_{n}^{IT+1} + \theta_1 \times \left( \mu_1 \times x_b - \mu_2 \times X_{n}^{IT} \right) + \theta_2 \times \delta \times \left( \mu_1 \times \operatorname{Mean}(X^{IT}) - \mu_2 \times X_{n}^{IT} \right), & \text{if } \mu_1 < 0.5 \\ x_b + \theta_1 \times \left( \mu_1 \times x_b - \mu_2 \times X_{n}^{IT} \right) + \theta_2 \times \delta \times \left( \mu_1 \times \operatorname{Mean}(X^{IT}) - \mu_2 \times X_{n}^{IT} \right), & \text{Otherwise} \end{cases} \end{equation}$$ XTAOIT​={XnIT+1​+θ1​×(μ1​×xb​−μ2​×XnIT​)+θ2​×δ×(μ1​×Mean(XIT)−μ2​×XnIT​),xb​+θ1​×(μ1​×xb​−μ2​×XnIT​)+θ2​×δ×(μ1​×Mean(XIT)−μ2​×XnIT​),​if μ1​<0.5Otherwise​​​
​
$$\begin{array}{c}{X}_n^{IT+1}=X_{TAO}^{IT}\end{array}$$
其中，rand表示(0,1)之间的均匀随机数，${\theta }_1$和${\theta }_2$分别是(−1,1)和(−0.5,0.5)之间的一致随机数，$DF$表示控制NRBO性能的决定因素，${\mu }_1$和${\mu }_2$是随机数，分别由公式(31)和(32)生成:
$$\begin{array}{rl}{\mu }_1& =\beta \times 3\times rand+(1-\beta )\\ {\mu }_2& =\beta \times rand+(1-\beta )\end{array}$$
其中$\beta$表示二进制数，即1或0，rand表示随机数。如果$\Delta$的值大于或等于0.5，则$\beta$的值为0；否则，该值为1。由于参数${\mu }_1$和${\mu }_2$选择的随机性，种群变得更加多样化，并逃离局部最优解，这有助于提高其多样性。与NRBO类似，GBO也受到牛顿方法的启发。因此，NRBO概念看起来可能与GBO相似，但由于NRBO的独特特性，其性能仍远优于GBO

流程图

伪代码

常见应用

工程中的非线性方程求解

在工程设计中，经常需要求解非线性方程。例如，在结构工程中，可能需要计算梁在特定载荷下的变形，这涉及到非线性材料特性和几何非线性方程的求解。

计算机图形学中的光线追踪

在光线追踪算法中，需要计算光线与复杂曲面（如多项式曲面）之间的交点。这通常涉及求解非线性方程组，牛顿-拉夫逊算法可以高效地逼近这些交点，从而渲染出真实感的图像。

金融工程中的期权定价

在金融工程中，Black-Scholes模型用于期权定价时，有时需要反解模型中的参数（如隐含波动率）。牛顿-拉夫逊算法可以用来求解隐含波动率，使得理论期权价格与市场价格相匹配。

优化问题

在许多优化问题中，尤其是涉及到寻找函数极值点的问题，牛顿-拉夫逊算法可以用来快速找到极值点。比如，在机器学习中的最优化算法中，用于训练神经网络的权重更新。

电力系统分析

在电力系统中，电力流分析需要求解一组非线性方程，以确定系统中电压和电流的分布。牛顿-拉夫逊算法被广泛应用于电力流计算，帮助电力工程师分析和优化电力传输。

化学反应动力学

在化学工程中，化学反应的动力学方程通常是非线性的。牛顿-拉夫逊算法可以用来求解这些方程，帮助工程师设计反应器和优化反应条件。

机器人运动规划

在机器人学中，运动规划问题涉及求解机器人的位置和角度，通常需要求解非线性方程组。牛顿-拉夫逊算法可以用来求解这些方程，从而规划机器人的路径。

本质是求解非线性方程组。它是一种迭代方法，通过逐步逼近来找到方程的根。该算法不仅适用于单个非线性方程的求解，也适用于多变量非线性方程组的求解。
27)表示：
x n I T + 1 = r 2 × ( r 2 × X 1 n I T + ( 1 − r 2 ) × X 2 n I T ) + ( 1 − r 2 ) × X 3 n I T X 3 n I T = X n I T − δ × ( X 2 n I T − X 1 n I T )

$$\begin{align} x_n^{IT+1} &= r_2 \times \left( r_2 \times X1_n^{IT} + (1 - r_2) \times X2_n^{IT} \right) + (1 - r_2) \times X3_n^{IT} \\ X3_n^{IT} &= X_n^{IT} - \delta \times \left( X2_n^{IT} - X1_n^{IT} \right) \end{align}$$ xnIT+1​X3nIT​​=r2​×(r2​×X1nIT​+(1−r2​)×X2nIT​)+(1−r2​)×X3nIT​=XnIT​−δ×(X2nIT​−X1nIT​)​​
其中$r_2$表示(0,1)之间的随机数。

陷阱规避操作（TAO）

纳入TAO是为了提高建议的NRBO处理现实世界问题的有效性。TAO是采用Ahmadianfar等人提出的改进和增强运算公式。使用TAO可以显著改变$x_n^{IT+1}$的位置。它通过组合最佳位置$X_b$和当前矢量位置$X_n^{IT}$来产生具有增强质量XITTAO的解决方案。如果rand的值小于$DF$，则使用如下公式产生解XITTAO：
X T A O I T = { X n I T + 1 + θ 1 × ( μ 1 × x b − μ 2 × X n I T ) + θ 2 × δ × ( μ 1 × Mean ⁡ ( X I T ) − μ 2 × X n I T ) , if  μ 1 < 0.5 x b + θ 1 × ( μ 1 × x b − μ 2 × X n I T ) + θ 2 × δ × ( μ 1 × Mean ⁡ ( X I T ) − μ 2 × X n I T ) , Otherwise

$$\begin{equation} X_{TAO}^{IT} = \begin{cases} X_{n}^{IT+1} + \theta_1 \times \left( \mu_1 \times x_b - \mu_2 \times X_{n}^{IT} \right) + \theta_2 \times \delta \times \left( \mu_1 \times \operatorname{Mean}(X^{IT}) - \mu_2 \times X_{n}^{IT} \right), & \text{if } \mu_1 < 0.5 \\ x_b + \theta_1 \times \left( \mu_1 \times x_b - \mu_2 \times X_{n}^{IT} \right) + \theta_2 \times \delta \times \left( \mu_1 \times \operatorname{Mean}(X^{IT}) - \mu_2 \times X_{n}^{IT} \right), & \text{Otherwise} \end{cases} \end{equation}$$ XTAOIT​={XnIT+1​+θ1​×(μ1​×xb​−μ2​×XnIT​)+θ2​×δ×(μ1​×Mean(XIT)−μ2​×XnIT​),xb​+θ1​×(μ1​×xb​−μ2​×XnIT​)+θ2​×δ×(μ1​×Mean(XIT)−μ2​×XnIT​),​if μ1​<0.5Otherwise​​​
​
$$\begin{array}{c}{X}_n^{IT+1}=X_{TAO}^{IT}\end{array}$$
其中，rand表示(0,1)之间的均匀随机数，${\theta }_1$和${\theta }_2$分别是(−1,1)和(−0.5,0.5)之间的一致随机数，$DF$表示控制NRBO性能的决定因素，${\mu }_1$和${\mu }_2$是随机数，分别由公式(31)和(32)生成:
$$\begin{array}{rl}{\mu }_1& =\beta \times 3\times rand+(1-\beta )\\ {\mu }_2& =\beta \times rand+(1-\beta )\end{array}$$
其中$\beta$表示二进制数，即1或0，rand表示随机数。如果$\Delta$的值大于或等于0.5，则$\beta$的值为0；否则，该值为1。由于参数${\mu }_1$和${\mu }_2$选择的随机性，种群变得更加多样化，并逃离局部最优解，这有助于提高其多样性。与NRBO类似，GBO也受到牛顿方法的启发。因此，NRBO概念看起来可能与GBO相似，但由于NRBO的独特特性，其性能仍远优于GBO

流程图

伪代码

常见应用

工程中的非线性方程求解

在工程设计中，经常需要求解非线性方程。例如，在结构工程中，可能需要计算梁在特定载荷下的变形，这涉及到非线性材料特性和几何非线性方程的求解。

计算机图形学中的光线追踪

在光线追踪算法中，需要计算光线与复杂曲面（如多项式曲面）之间的交点。这通常涉及求解非线性方程组，牛顿-拉夫逊算法可以高效地逼近这些交点，从而渲染出真实感的图像。

金融工程中的期权定价

在金融工程中，Black-Scholes模型用于期权定价时，有时需要反解模型中的参数（如隐含波动率）。牛顿-拉夫逊算法可以用来求解隐含波动率，使得理论期权价格与市场价格相匹配。

优化问题

在许多优化问题中，尤其是涉及到寻找函数极值点的问题，牛顿-拉夫逊算法可以用来快速找到极值点。比如，在机器学习中的最优化算法中，用于训练神经网络的权重更新。

电力系统分析

在电力系统中，电力流分析需要求解一组非线性方程，以确定系统中电压和电流的分布。牛顿-拉夫逊算法被广泛应用于电力流计算，帮助电力工程师分析和优化电力传输。

化学反应动力学

在化学工程中，化学反应的动力学方程通常是非线性的。牛顿-拉夫逊算法可以用来求解这些方程，帮助工程师设计反应器和优化反应条件。

机器人运动规划

在机器人学中，运动规划问题涉及求解机器人的位置和角度，通常需要求解非线性方程组。牛顿-拉夫逊算法可以用来求解这些方程，从而规划机器人的路径。

本质是求解非线性方程组。它是一种迭代方法，通过逐步逼近来找到方程的根。该算法不仅适用于单个非线性方程的求解，也适用于多变量非线性方程组的求解。