中级软考-软件设计师（四）_下表为某文件中字符的出现频率,采用霍夫曼编码对下列字符编码,则字符序列“bee”

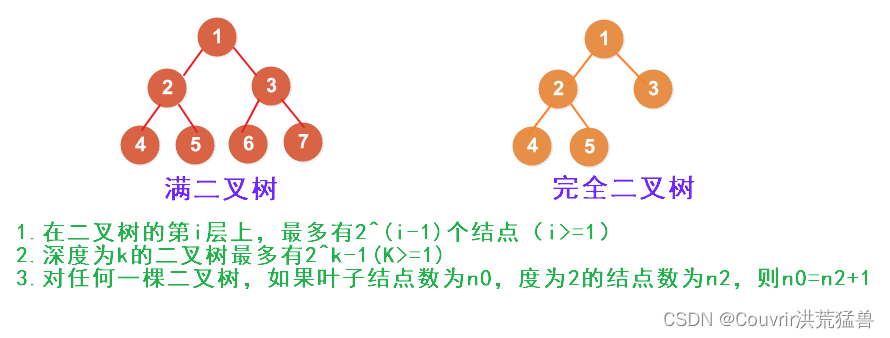
数据结构

1.哈夫曼数

构造哈夫曼树，左小右大，左0右1。下图反了。

哈夫曼树是个没有度为1的二叉树，即n=n0+n2。对于任意树，有n0=n2+1。所以，对于哈夫曼树，n=2n2+1=2n0-1。

下列为某文件中字符的出现频率，采用哈夫曼编码对下列字符编码，则字符序列“bee”的编码为101 1101 1101。字符有6个，占3位二进制，则码长为3。

2.贪心算法

在对问题求解时，总是做出在当前看来是最好的选择。非整体最优，为局部最优。

3.分治算法

将数据分成若干份，每份单独处理后再合并。

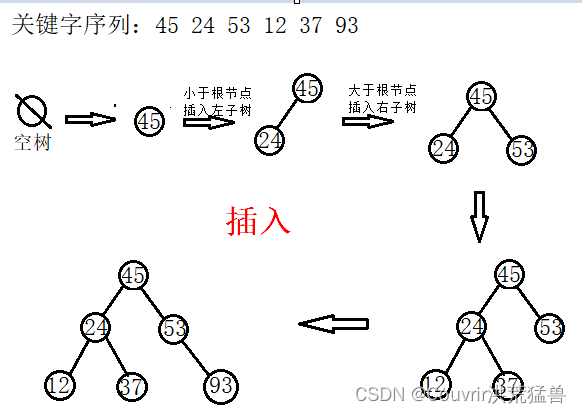
4.二叉排序树（二叉查找树）

二叉排序树中没有值相同的节点。或者是一棵空树；或者是具有下列性质的二叉树：

1)若它的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；

2)若它的右子树不为空，则右子树上所有节点的值均大于它的根节点的值；

3)它的左、右子树也分别为二叉排序树。

二叉树的顺序存储采用数组存储：对于下标为i的结点，左子树下标为2i，右子树下标为2i+1。

树结点的度是结点所拥有的分支的数目。

二叉排序树查找效率与深度有关。

二叉排序树中序遍历，可得到该二叉树中结点关键字的有序序列，根结点肯定是关键码序列的第一位。

平衡二叉树：任意结点的左右子树深度相差不超过1；

平衡度=左子树深度-右子树深度。每结点的平衡度只能为-1、0、1。

完全二叉树：除了最底层，上面层为满二叉树。最底层，结点从左到右排序，不行成空缺。

单枝数效率最差。

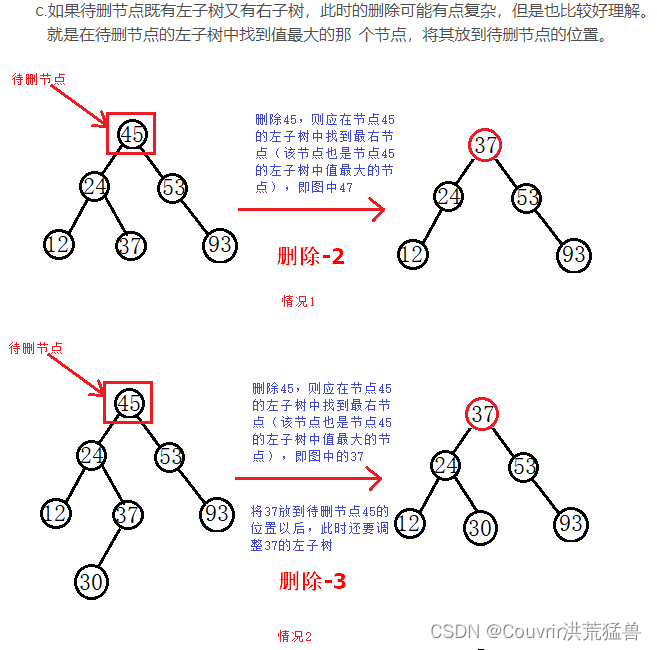
删除结点操作： 

 

二叉树的重要特性

5.等比求和和等差求和

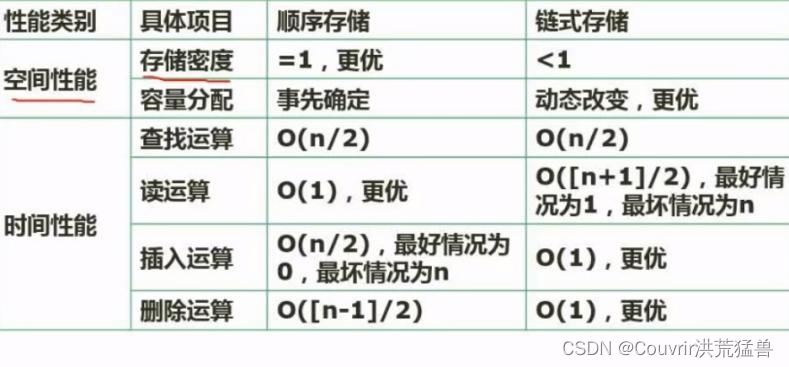
6.n个元素，等概率删除元素操作。若顺序存储结构，则平均需要移动（n-1）/2个元素。若链式存储结构，则平均需要移动0个元素。

7.若在单向链表上，除访问链表中所有结点外，还需在表尾频繁插入结点或删除最后一个结点，采用仅有尾指针的单循环链表最节省时间和存储空间。

8.图 

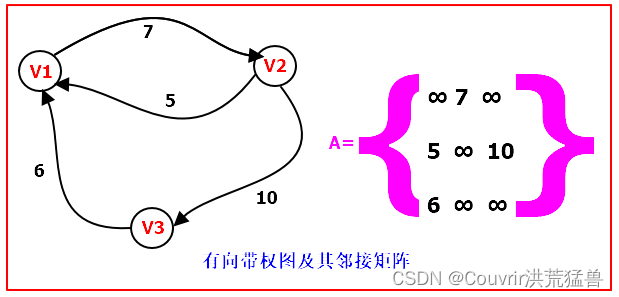
权：图边上的数字。

网：带权的图。

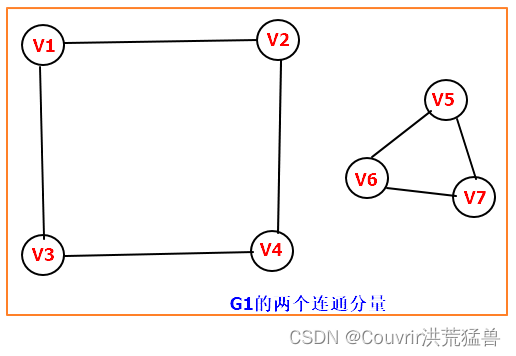
连通图：任意两顶点都是连通的图。

连通分量：无向图的极大连通子图。

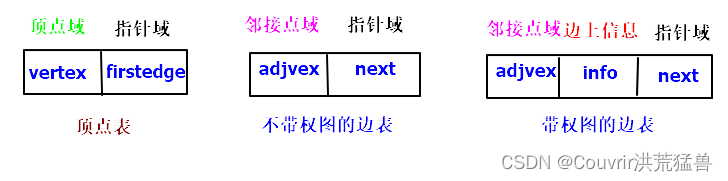
图没有顺序存储的方式。图的存储结构：邻接矩阵和邻接表。

   

9.无向图 

无向图中若有n个顶点、e条边，则它的邻接表需要n个表头指针和2e个边结点。

有向图中若有n个顶点、e条边，则它的邻接表需要n个表头指针和e个边结点。

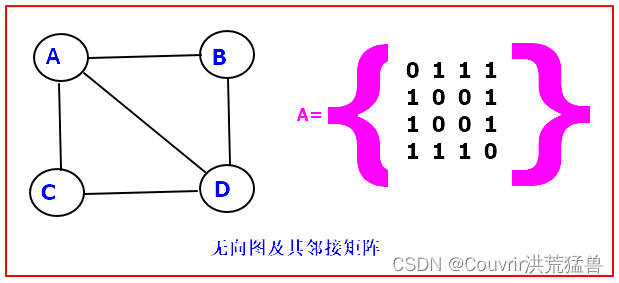
n个结点，e条边的邻接矩阵有n^2个元素。对于有向图，邻接矩阵非零元素个数为e。对于无向图，邻接矩阵非零元素个数为2e。无向图中深度优先遍历，时间复杂度为O(n^2)。

无向图的邻接矩阵是对称的，而有向图的邻接矩阵不一定对称。

无向图中顶点的度是指与该顶点相邻的顶点数。

对于无向图，顶点Vi的度是邻接矩阵中第i行(或第i列)的非零元素的个数。

对于有向图，顶点Vi的度是邻接矩阵中第i行和第i列的非零元素的个数之和。

10.深度优先搜索和广度优先搜索

深度用栈实现，使用递归方式。

广度用队列实现。

连通图，从图的任意一顶点开始深度或广度优先遍历一定可以访问图中的所有顶点。

非连通图，从图的任意一个顶点开始深度或广度优先遍历并不能访问图中的所有顶点。

11.用哈希表存储元素时，需要进行冲突处理，冲突是指关键字不同的元素被映射到相同的存储位置。

12.时间复杂度递归式T(n)=T(n-1)+n，n为问题的规模，则时间复杂度为O(n^2)。若问题的规模增加了16倍，则运行时间增加256倍。

假设T(1)=1， T(n)=T(n-1)+n=T(n-2)+n-1+n=T(n-3)+n-2+n-1+n=...=T(n-(n-1))+n(n-1)-(1+2+...+(n-2))=1+n(n-1)-(n-2)(n-1)/2=1+(n-1)(n+2)/2。

13.散列存储结构的特点是数据结构中元素的存储地址与其关键字之间存在某种映射关系。

14.树的遍历

先序遍历：根左右

中序遍历：左根右

后序（后缀）遍历：左右根

任何一棵二叉树的叶结点在先序、中序和后序序列中的相对次序不发生改变，发生改变的是子树的根，也就是分支结点。

15.二叉树采用二叉链表时，空指针个数为结点数+1；二叉树采用三叉链表时，空指针个数为结点数+2；

16.深度优先搜索

类似于树的先序遍历，是树的先序遍历的推广。

(1)首先从图中某个顶点v出发， 首先访问此顶点，将其标记为已访问过;

(2)然后任选一个v的未被访问的邻接点w出发，继续进行深度优先搜索;

(3)直到图中所有和v路径相通的顶点都被访问到;

(4)若此时图中还有顶点未被访问到，则另选一个未被访问的顶点作为起始点，重复上面的步骤，直至图中所有的顶点都被访问。

17.广度优先搜索

类似于树的按层次遍历。

假设从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直至图中所有已被访问的顶点的邻接点都被访问到。

若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

18.若该队列的容量为M，则长度为(Q.rear-Q.front+M)%M。

队列长度为Q.rear-Q.front。队列中存储位置编号为：0~M-1。

19.栈的应用：表达式求值、括号匹配、递归调用。队列的应用：打印序列。

逆波兰式是后缀表达式，需要用栈来运算。

20.Prim算法和 Kruscal算法

都基于贪心算法。

Prim算法的时间复杂度为O(n2)，与图中边数无关，该算法适合于稠密图。

Kruskal 算法的时间复杂度只和边有关系，为O(elog2e)，由于 Kruskal 算法只与边有关，因此适合求稀疏图的最小生成树。

普利姆算法：

任选一个结点变成红点，其余为蓝点。

在它能一步到位的蓝点中选择权值最小的路径，路径末的结点变成红点。

在红点群中选择它能一步到位的蓝点权值最小的路径，路径末的结点变成红点。以此循环。注意，不能形成环路。边数=结点数-1。

克鲁斯卡尔算法：先选最短的边，循环选最短的边。注意，不能形成环路。边数=结点数-1。

21.优先队列一般采用二叉堆数据结构实现，由于是二叉堆，所以插入和删除一个元素的时间复杂度均为O(lgn)。

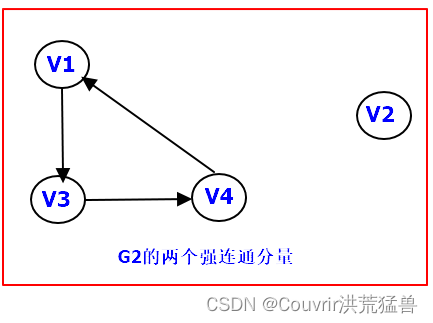
22.某有向图的邻接表如下，可看出存在弧<v2，v3>，而不存在从顶点v1出发的弧。

23. 单链表存储结构

24. 递归下降分析方法是一种自上而下的语法分析。

25.一颗度为3的树，1度的结点数：5，2度的结点数：4，3度的结点数：2。那么叶子结点数为9。

总度数为5*1+2*4+3*2=19，即除根结点外，有19个结点，所以总结点数=20。叶子结点数=20-5-4-2=9。

26.数组的存储地址

27.顺序存储和链式存储 

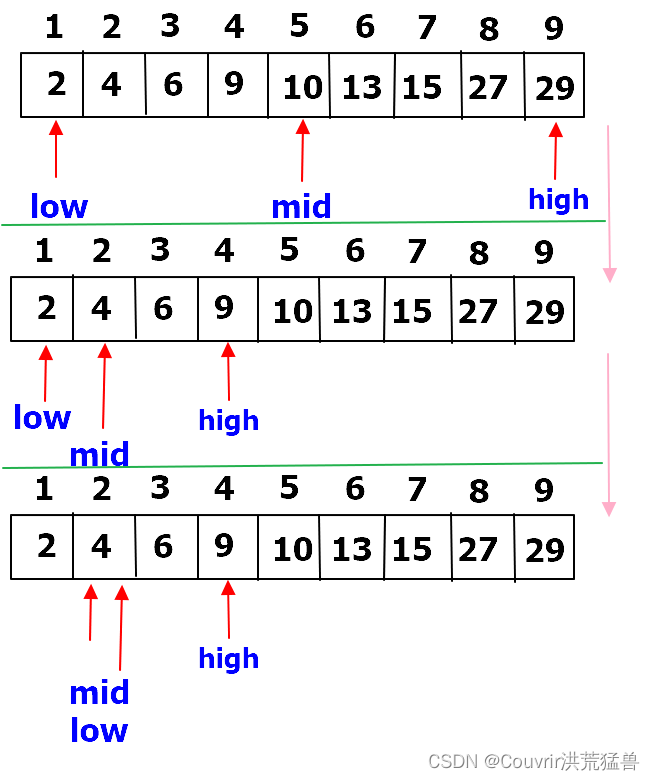
28. 折半查找（二分查找）

前提：查找表必须是按关键字大小有序排列的顺序表。查找速度快，插入删除困难。

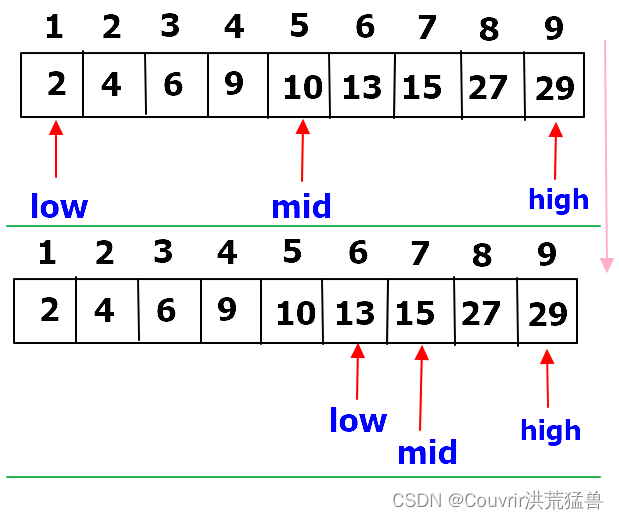
有关键字序列[2,4,6,9,10,13,15,27,29]采用折半查找法查找6和17的具体过程。

解:设low为低位指针，high为高位指针，mid为中间位置指针。

其中，mid=(low+high)/2，若mid所指元素大于关键字k时，这时令high=mid-1，向 mid 前一半的表中继续查找。若mid所指元素小于关键字k时，这时令low=mid+1，向mid后一半的表中继续查找。当 high<low时，表示不存在这样的查找子表空间，查找失败。

1)查找k=6的过程。

初始时令low=1，high=9，则mid=5。

此时因为 k=6<r[mid]=10，所以high=mid-1=4, mid=(low+high)/2=(1+4)/2=2。

此时因为 k=6>r[mid]=4，所以low=mid+1=3，mid=(low+high)/2=(3+4)/2=3。

此时 k=r[mid]=6，查找成功。

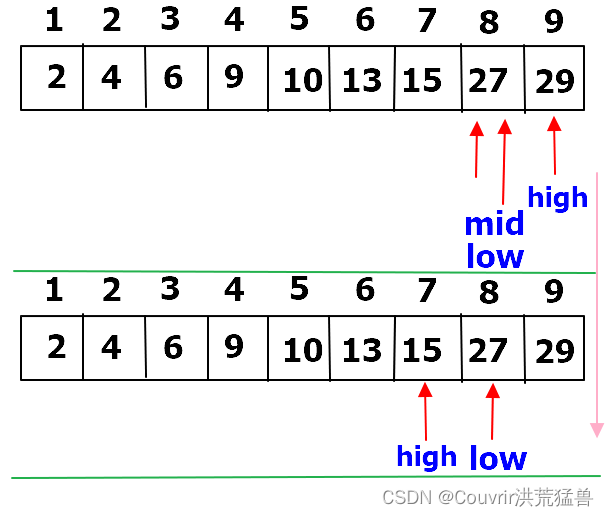
2)查找k=17的过程。

初始时令low=1，high=9，则mid=5。

此时因为 k=17>r[mid]=10，所以low=mid+1=6，mid=(low+high)/2=(6+9)/2=7。

此时因为 k=17>r[mid]=15，所以low=mid+1=8，mid=(low+high)/2=(8+9)/2=8。

此时因为 k=17<r[mid]=27，所以high=mid-1=7。

因此此时high=7<low=8，说明查找区间为空，查找失败，即17不在表中。

29.选择排序：直接选择排序和堆排序，都不稳定。

工作原理：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

例如序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序是一个非稳定的排序算法。

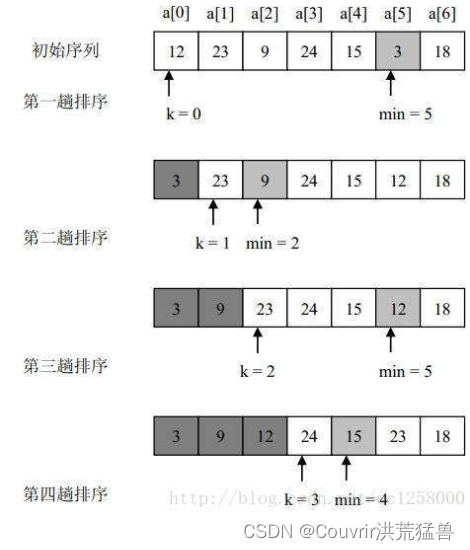
30.直接选择排序，属于选择排序。

设待排序的记录序列有n=7个记录，其关键字的初始序列为 :(35,22,8,16,21,22,27)，请给出直接插入排序的过程。在序列中有两个相同关键字22，后一个22将用方框标出以示区分。

31.堆排序，属于选择排序，时间复杂度为O(nlog2n)

设有n个元素的序列{K1,K2,...,Kn}，当且仅当满足下述关系之一时，称之为堆。

Ki<=k2i且ki<=k2i+1 小顶堆

Ki>=k2i且ki>=k2i+1 大顶堆

32.直接插入排序，属于插入排序。

当插入第i个记录时，R1，R2，...，Ri-1均已排好序，因此，将第i个记录Ri依次与Ri-1，...，R2，R1进行比较，找到合适的位置插入。比较的时候是从右往左比。它简单明了，但速度很慢。

例：设待排序的记录序列有n=7个记录，其关键字的初始序列为 :(32,15,6,48,19,15,27)，请给出直接插入排序的过程。在序列中有两个相同关键字15，后一个15将用方框标出以示区分。 放监视哨 

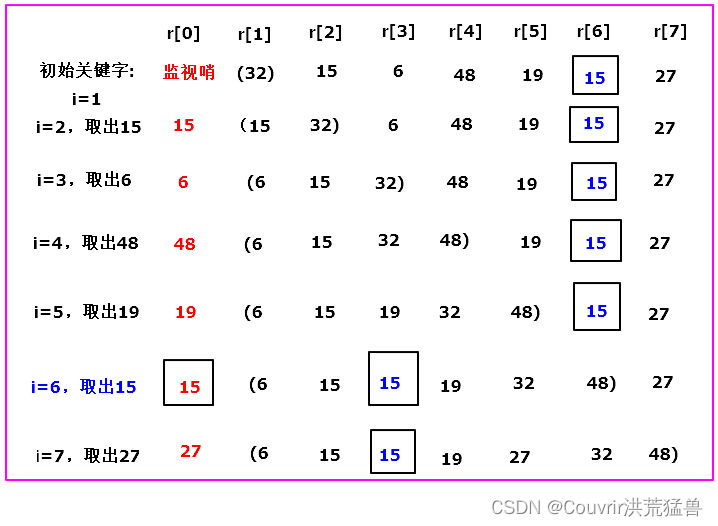
[5，2，4，6，1，3]采用插入排序算法进行从小到大排序，需要进行12次整数之间的比较。 输入数据具有从大到小排列时，对整数进行从小到大排序，所需的比较次数最多。

33.希尔排序，属于插入排序。

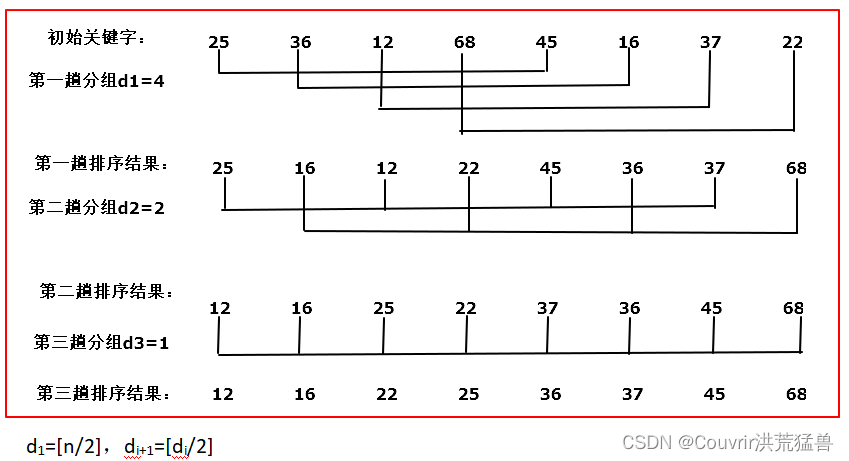
已知待排序的一组记录的关键字初始序列为 :(25,36,12,68,45,16,37,22)，请给出希尔排序的过程。

34.冒泡排序，属于交换排序。 

从左到右，两两比较后排序，排序完固定最后的序列关键字。

进行下一轮，以此循环。

每经过一趟冒泡排序，都是无序区中关键字值最大的记录进入有序区，对于由n个记录组成的记录序列，最多经过n-1趟冒泡排序，就可以将这n个记录重新按关键字顺序排列。

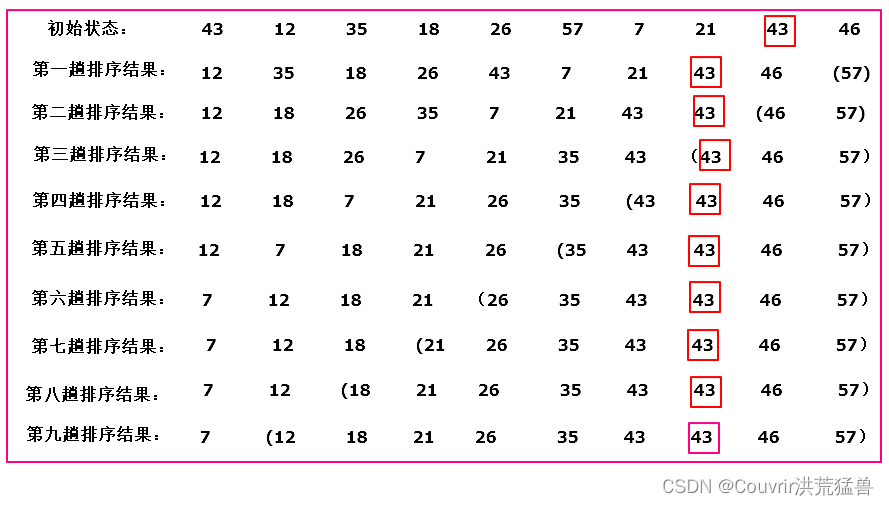
已知有10个待排序的记录，它们的关键字序列为 :{43,12,35,18,26,57,7,21,43,46}，请给出冒泡排序法进行排序的过程。(两个相同关键字43，后一个43将用方框标出以示区分)

35.快速排序，属于交换排序。 基准元素选择中位数，待排序列适合采用顺序存储。采用分治算法。

已知一个无序序列，其关键字值为{32,42,7,48,15,48,12,18}的记录序列，都给出进行快速排序的过程。(其中有两个相同的关键字48，后一个用方框括起)

36.归并排序 

将n个记录的待排序序列看成是有n个长度都为1的有序子表组成。

将两两相邻的子表归并为一个有序子表。

重复上述步骤，直至归并为一个长度为n的有序表。

对具有初始输入序列(26,5,77,1,61,11,59,15)的记录采用归并排序法进行排序，序列在每遍扫描时合并的情况如下图所示。其中h为归并排序的有序表中元素个数，n为表总长度。初始h=1 ，以后 hi+1=2hi，当n>h时进行归并排序，当n<h时结束归并排序。

 

37.排序方法总结

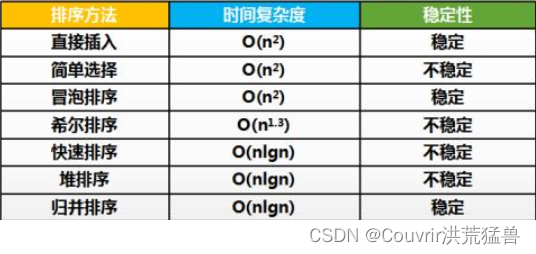
大多数内部排序算法都只适用于顺序存储。

38.在某应用中，需要先排序一组大规模的记录，其关键字为整数。

若这组记录的关键字基本上有序，则适宜采用插入排序算法。

若这组记录的关键字的取值均在0到9之间(含)，则适宜采用计数排序算法。

39. 申请场地举办活动，每个活动有开始时间和结束时间。在同一个场地，如果一个活动结束之前，另一个活动开始，即两个活动冲突。若活动A从时间1开始，5时间结束。活动B从5时间开始，8时间结束，则活动A和B不冲突。现要计算n个活动需要的最少场地数。采用快速排序方法。下表给出n=11的活动集合，得出最少的场地数为5。

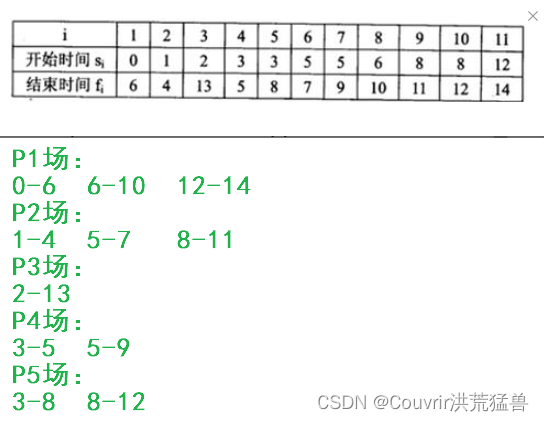
40.广义表