基于分数阶傅里叶变换和相位分析技术的OFDM雷达距离精度增强_傅里叶变换观察窗

FMCW线性调频连续波雷达的测量速率往往受到扫频速度的限制。单音或双音干涉仪技术可以实现对目标的高速率测量，但当目标超出有限距离窗口时，就会产生距离模糊。由于毫米波频率高、波长短，通过确定载波相位可以实现超高的测距精度，而OFDM通过码分的方式可以抵抗干扰。因此，毫米波OFDM雷达传感器实现了强干扰下的高精度测量。

在[16]中提出了正交频分复用雷达波形，可以同时进行雷达探测和通信。基于对每个传感器应用不同的特征码，多部雷达可以同时无干扰地工作。应用FFT时，OFDM雷达的距离精度和分辨率与发射信号的带宽B成反比，δR = c 0 /2B，其中c 0为光速。

距离分辨率是雷达在距离维度上辨别两个或更多物体的能力。当两个物体相对于雷达的距离近到某个特定值时，雷达便不能再将二者区分开，将两个物体分辨为同一个物体

OFDM背景

一个OFDM多载波信号可以表示为多个平行的正交信号载波信号经过不同传输数据调制后的复合。其公式为：

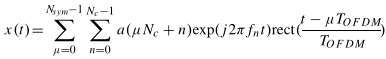
假设一个传输波形由$N_{sym}$个符号组成，每个符号的符号时长为$T_{sym}$，则每个符号为$N_{c}$个子载波的和，子载波间距为$\Delta f=1/T_{sym}$。每个子载波在每个符号处的初始相位如图所示

其中

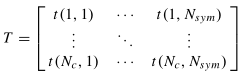
矩阵T中的每一个元素都是一个复数用来表示传播的阶段;第一个索引表示子载波号，第二个索引表示符号号，一个波形一共有$N_{c}N_{sym}$个符号。对于每个发射机，矩阵T被固定为一个 signature code.

文中采用BPSK调制，因此 t (m , n) ∈ [0 , π]。如果接收机与发射机完全同步，从目标反射的回波将产生一个延迟 $\tau$ 的绿色波.

研究内容

论文的研究重点是如何高精度地估计这种延迟

通过设计足够宽的观察窗，可以完全捕捉接收回波。由于接收器与发射器完全同步，接收信号矩阵可构造类似于矩阵T，接收信号矩阵R可表示为

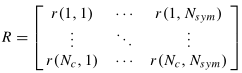
 所接收的信号包含延迟信息（关注重点）

通过将矩阵R与矩阵T分割，可以用矩阵D = R/T在时域和频域对信道进行建模。

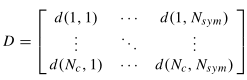
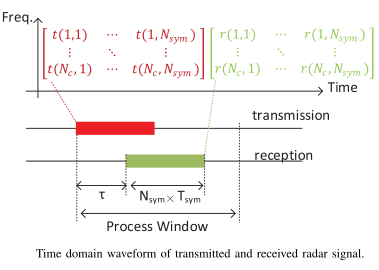
为便于理解，矩阵T和R如图所示

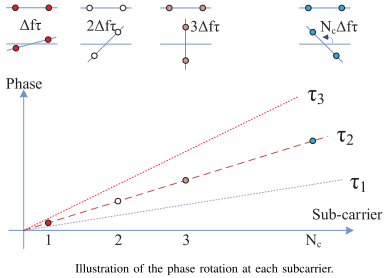
4个BPSK星座图以不同颜色显示，分别对应子载波1、子载波2、子载波3和子载波$N_{c}$.

子载波1的星座图对应矩阵 T 的第一行。下面的星座图是接收到的不同子载波的星座图。类似地，每个组合图对应于矩阵R中的某一行。可以注意到，当单个目标出现时，高载波星座比低载波星座旋转角更大。

D中的每一行表示每个子载波上的星座旋转测量值。这样的测量在接收每个符号时进行，因此每行有$N_{sym}$个数据。

对每一行进行平均，因此矩阵D转换为向量：

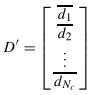
 其中是第m个子载波处星座图平均旋转的复数

上图的底部绘制了向量 D' 沿y轴的角度和沿x轴的每个子载波的频率

对于理想单目标，旋转角度随子载波频率的增加呈线性增加，因此在第k个子载波处的旋转角度为:

 在[16]中提出了一种利用IDFT运算的距离估计方法:

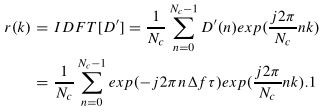
 可以看出，当有两个指数项会相互抵消。这意味着在r(k)的时间响应的索引在k处会出现一个峰值，表明在该位置检测到目标

使用这种方法的准确性受限于IDFT的使用。可以看出，目标范围搜索是在的离散步长内进行的

在上面的相位旋转图中用几条不同斜率的虚线参考线来比较观察到的旋转角度。直观地说，使用更多的参考线和更细的步骤将给出更准确的估计。

FRFT和相位分析技术

 提出了一种两步信号处理方法，可将测距精度提高到微米级：

第一步是使用FRFT代替傅里叶变换。

第二步利用载波的相位信息进一步提高估计精度。

1.用FRFT提高距离精度

通过简单地添加更多的搜索步骤来修改利用IDFT运算的距离估计公式将提高估计精度。通过引入分数阶因子ma（分数因子定义了搜索的ma时间点），基于FRFT的估计函数可表示为

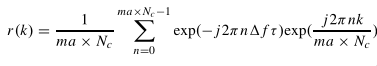
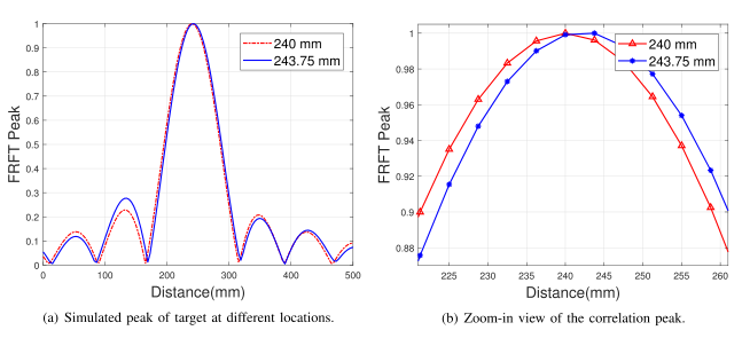
下图中为采用FRFT方法的仿真结果，仿真场景为:128个子载波，间距为15.625 MHz, ma = 20，载波频率为80 GHz，目标距离设置为240 mm和243.75 mm。模拟目标在240 mm和243.75 mm处的FRFT相关峰

当使用利用IDFT运算的距离估计公式时，这两个位置的目标产生相同的峰值，表明估计距离为75mm，结果表明  传统方法无法跟踪这么小的距离变化  

下图是利用FrFT运算的距离估计公式得出的结果

 可以从图中看出，由于估计曲线具有较好的精度，可以以较高的置信度跟踪目标运动。

在低信噪比(SNR =−10 dB)的情况下也进行了仿真。正如预期的那样，相关性峰值并不像理想情况下那样明显。为了解决这个实际问题，将图c中的曲线与一个理想的“sinc”函数进行关联，如下式所示，然后在此过程后，相关峰再次出现。

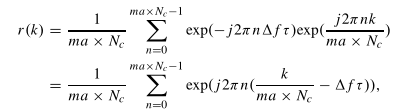
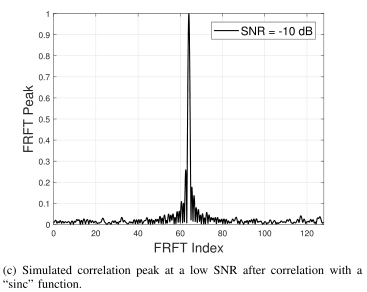
 方程可以进一步简化为

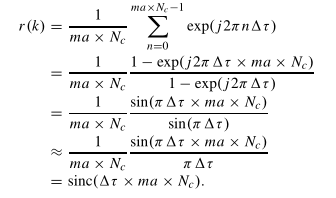
可达距离精度取决于几个系统参数，如信噪比、正交平衡、带内平坦度等。

在本系统中，相关法仅用于粗估计。只要估计精度优于载波波长，就可以利用相位估计进一步提高精度到微米级。

2.相位分析增强距离精度

利用毫米波载波的短波长，即使在微米级目标位移时也会发生相位旋转。通过检测调制载波的相位，可以以微米级精度跟踪目标的距离。被干涉仪雷达广泛使用，但是当目标移动超过一个载波波长时，会产生模糊。

所提出的FRFT方法可以以小于半个波长的精度定位目标。增加相位分析可以进一步提高精度到微米级。目标的距离可以表示为:

 对于OFDM符号中的任何子载波，目标等于载波波长的m倍，剩余距离为 R’ 。利用之前FRFT方法得到的距离估计值$\hat{R}_{OFDM}$计算整数m，通过量化过程消除估计误差。剩余距离的计算方法如下:

 其中 $\phi$ 是接收到的星座在波长 $\lambda _{c}$ 的子载波上的旋转。例如，在80 GHz ( = 3.75mm)， 0.1°旋转等于 1 um 目标运动，然后将距离估计精度转化为星座旋转的角度分辨率。

目标距离可以通过上式加上一个宽无模糊窗（wide unambiguous window）进行估计。

多雷达干扰消除

所提出的OFDM雷达在感知目标时利用 signature code。使用多重signature code，雷达可以紧密安装而互不干扰。

如上所述，雷达传输特定的符号序列 T，如之前的T所示。通过为不同的雷达分配正交符号序列，可以使雷达之间的干扰最小化。论文中，选择的发射符号序列是一个m序列，它是由多项式利用线性反馈移位寄存器技术产生的。通过为不同的雷达分配不同的m序列码，雷达可以同时工作。为了了解雷达在干扰下的性能，使用一种雷达在另一种雷达的影响下运行的情况进行仿真。模拟了在同一频段内工作的另一雷达对OFDM雷达距离精度的影响

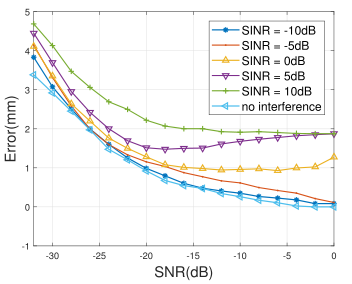
在仿真中，128位m序列被分配给两台工作在相同频率的雷达。目标距离误差根据接收信噪比绘制。首先，当只有一台雷达工作时，估计误差绘制为“无干扰”。然后加入另一个带内工作的雷达，干扰信噪比(SINR)变化在- 10 dB到10 dB之间

SINR (Signal to Interference plus Noise Ratio)代表干扰信噪比，定义如下。简单地说，SINR是信号（期望信号）和无用噪声的比值。不需要的噪声包括所有外部干扰和内部产生的噪声。

仿真结果如下：

• 在信噪比为- 22 dB、干扰信噪比为5 dB时，估计误差小于载波波长(79 GHz, 1.85 mm)的一半。
• 由于估计是对128个子载波进行平均，因此该雷达对带内干扰具有较强的免疫力。当信干噪比(SINR) = 10db时，雷达也能正常工作。
• 仿真结果表明，在干扰信噪比为5 dB时，仍可在信噪比为−22 dB时实现半波长估计。这意味着在信噪比为−22 dB时，当信噪比为5 dB时，通过相位分析可以进一步提高测距精度

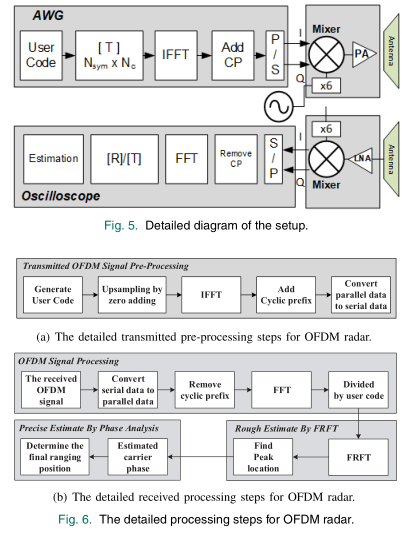
传输预处理过程：一开始生成用户代码以区分每个用户。然后我们通过加零进行上采样。然后，利用IFFT产生OFDM信号;此外，添加循环前缀以抵抗多路径问题。最后，将并行数据转换为串行数据。

接收处理过程：在第一阶段，对OFDM信号进行处理。首先将串行数据转换为并行数据，然后去除OFDM信号中的循环前缀。然后利用FFT对OFDM信号进行解调。最后，通过除以用户代码可以唯一地留下相位信息（论文中使用的是BPSK），在第二阶段，可以利用FRFT的峰值位置进行粗略估计。在最后一阶段，由于第二阶段的估计精度已经在一个波长内，因此可以采用相位分析进一步提高距离精度。

利用FRFT使目标的测距精度在毫米波的一个波长内，再利用载波相位分析方法进一步提高测距精度。

利用OFDM的并行特性和毫米波的短波长特性，论文提出的OFDM雷达可以在较长的无模糊范围内以较高的刷新率实现高精度。