数据结构--时间复杂度和空间复杂_select from 时间复杂度

先自我介绍一下，小编浙江大学毕业，去过华为、字节跳动等大厂，目前阿里P7

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年最新大数据全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上大数据知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以添加V获取：vip204888 （备注大数据）

正文

时间复杂度的概念

大O的渐进表示法

常见时间复杂度计算举例

空间复杂度

空间复杂度的概念

常见空间复杂度计算举例

常见复杂度对比

复杂度的oj练习

---

前言

随着近些年计算机快速的发展，对程序员来说入职要求也越来越高了，公司对我们的代码能力要求也越来越高了，大厂笔试中几乎全是算法题而且难度大，中小厂的笔试中才会有算法题，所以现在也越来越卷。为了能有一份好工作，我们必须手撕数据结构。难道就只是入职也一好处吗？显然不是的，学好算法不论对你思考问题的方式还是对你编程的思维都会有很大的好处。

什么是数据结构

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。

---- 来自百度

数据结构与数据库

那么数据结构与数据库有什么关系呢？

数据结构：内存中管理数据–增删改查

数据库：    磁盘中管理数据–增删改查

什么是算法

算法(Algorithm):就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。列如在我学习c语言中：二分查找，冒泡等

算法和数据结构的关系

数据结构和算法是相辅相成的。数据结构是为算法服务的，算法要作用在特定的数据结构之上。如果不在的基础上操作、构建算法，孤立存在的数据结构就是没用的。

时间复杂度

算法的复杂度

算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

**时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。**在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

推导大O阶方法：

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

使用大O的渐进表示法以后，Func1的时间复杂度为：O(N^2)

N = 10 F(N) = 100

N = 100 F(N) = 10000

N = 1000 F(N) = 1000000

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数(下界)

例如：在一个长度为N数组中搜索一个数据x

最好情况：1次找到

最坏情况：N次找到

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

常见时间复杂度计算举例

例题1

void Func2(int N){
    int count = 0; 
	for (int k = 0; k < 2 * N; ++k)
	 {       
		 ++count; 
	 }   
	int M = 10; 
	while (M--)
	{     
		++count;  
	}
	printf("%d\n", count); 
}
1
2
3
4
5
6
7
8
9
10
11
12
13

计算次数时间复杂度函数式：2*N+10

时间复杂度：O(N)

对于一个极大的数来说，乘一个常数与加一个常数都不能改变他的量级。比如一个亿万富翁，给他加几万或者在翻一倍，他变了好像又没有变，他还是亿万富翁。

例题2

void Func3(int N, int M){
	int count = 0; 
	for (int k = 0; k < M; ++k)
	{
		++count; 
	}
	for (int k = 0; k < N; ++k)
	{
		++count; 
	}
	printf("%d\n", count); 
}
1
2
3
4
5
6
7
8
9
10
11
12

时间复杂度：O(N+M)

如果M远大于N ,时间复杂度:0(M);  N远大于M ，时间复杂度：O(N); M与N一样大，时间复杂度O(M)或者O(N)

例题3

void Func4(int N)
{    int count = 0; 
	for (int k = 0; k < 100; ++k)
	{
		++count; 
	}
	printf("%d\n", count);
}
1
2
3
4
5
6
7
8

时间复杂度：O(1)

这里的1并不是1次，代表的是常数次

例题4

const char * strchr(const char * str, int character);                        ----查找字符串的字符

时间复杂度：O(N)

最好次数1次找到，最坏次数N次找到，平局次数N/2，在实际情况下我们一般关注的是最坏运行情况，所以数组中搜索数据的时间复杂度是O(N)。有这样一句比较有哲理的话：**用悲观的心态过积极的人生。**在生活中做最坏的打算也不一定有最坏的结果。

例题5

#include  <stdio.h>

void BubbleSort(int* a, int n)//冒泡排序
{
	assert(a); 
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0; //优化
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
		{
				Swap(&a[i - 1], &a[i]);
		exchange = 1; 
			}
		}
		if (exchange == 0)
			break; 
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

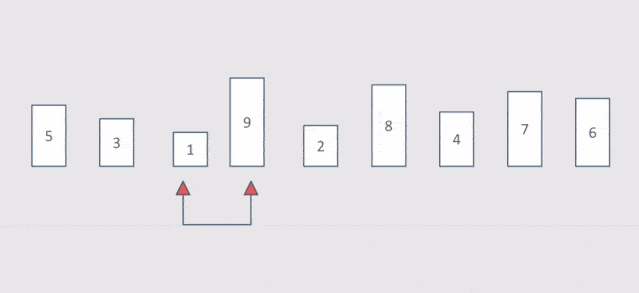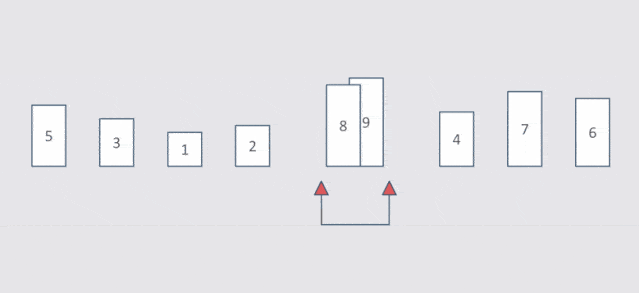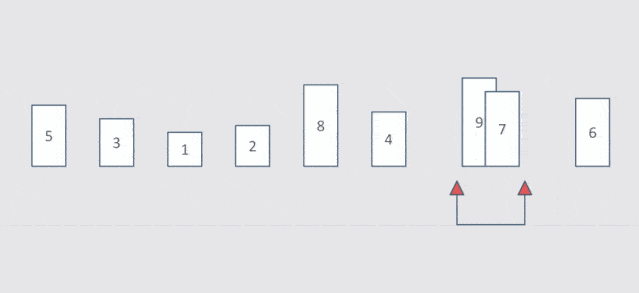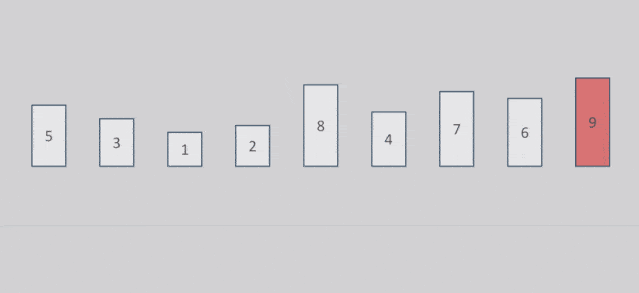
时间复杂度：O(N^2)

计算过程：N-1+N-2+…+2+1=N*(N-1)/2

例题6

int BinarySearch(int* a, int n, int x) //二分查找
{
	assert(a); 
	int begin = 0; 
	int end = n - 1; 
	// [begin, end]：begin和end是左闭右闭区间，因此有=号
	while (begin <= end)
	{
		int mid = begin + ((end-begin)>>1);
		if (a[mid] < x)
			begin = mid+1;
		else if (a[mid] > x)
			end = mid-1;
		else
			return mid;
	}
		return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

时间复杂度：O(logN)

计算过程：N/2/2…/2=1 —> N=2^x —>x=log(2)N

例题7

long long Fac(size_t N)
{
	if (0 == N)
		return 1;
	return Fac(N - 1)*N; 
}
1
2
3
4
5
6

时间复杂度：O(N)

计算过程：Fac(N)->Fac(N-1)->Fac(N-2)->…->Fac(2)->Fac(1)

例题8

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）**
![img](https://img-blog.csdnimg.cn/img_convert/a78b33aac971f1342e1c3288057646e8.png)

**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

return Fac(N - 1)*N; 
}
1
2
3
4
5
6
7
8
9
10
11

时间复杂度：O(N)

计算过程：Fac(N)->Fac(N-1)->Fac(N-2)->…->Fac(2)->Fac(1)

例题8

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）**
[外链图片转存中...(img-fgRdfyc2-1713408974749)]

**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

1
2
3
4
5
6
7
8
9