进化算法——多目标优化_多目标优化算法

所有的实际优化问题都是多目标的，如果不是显式的至少也是隐式的。接下来讨论多目标优化问题（MOP）如何修改进化算法。实际的优化问题包含多个目标，那些目标常常互相冲突。例如：

• 在购买汽车时，我们可能想要车最舒适并且花钱最少。最舒适的汽车太贵，最便宜的汽车又不太舒服。
• 在设计一座桥时，我们可能想让它的费用最低强度最大。用泡沫塑料建造的桥可能费用最低，但他非常脆弱。用钛合金建造的桥可能强度最大但它非常昂贵，在费用和强度之间如何才是最好的折中？

MOP又被称为多准则优化、多性能优化，以及向量优化。假定独立变量x为n维向量，并假定MOP是最小化问题。MOP可以写成如下的形式：

MOP的目标是同时最小化k个函数。

MOP常常包含约束，我们不处理带约束的MOP。我们可以将约束融入多目标进化算（MOEAs），其方式与将约束融入单目标进化算法相同。

---

目录

帕累托最优性

​支配

多目标优化的目标

1.超体积

2.相对覆盖度

基于非帕累托的进化算法

1.集结方法

 凹帕累托前沿的目标达成

2.向量评价遗传算法

3.字典排序

 4.​-约束方法

 5.基于性别的方法

基于帕累托进化算法

1.多目标进化优化器

a.简单多目标进化优化器（simple evolutionary multi-objective optimizer，SEMO）

b.多样性多目标进化优化器（divercity evolutionary multi-objective optimizer，DEMO） 

2.基于​的多目标进化算法

3.非支配排序遗传算法NSGA

NSGAⅡ

4.多目标遗传算法 

5.小生境帕累托遗传算法NPGA

6.优势帕累托进化算法SPEA

SPEA2

7.帕累托归档进化策略PAES

基于生物地理学的多目标优化

1.向量评价BBO

2.非支配排序BBO

3.小生境帕累托BBO

4.优势帕累托BBO

---

 

帕累托最优性

我们首先列出在多目标优化中经常用到的一些定义。

1.支配。称点支配x如果下面的两个条件成立：（1）对所有i∈[1,k]，并且（2）对至少一个j∈[1,k]，＜，即对所有目标函数值，至少与x一样好，并且至少有一个目标函数值比x好，用记号

表示支配x，符号表示的函数值小于或等于x的函数值。

2.弱支配。 称点弱支配x如果对所有i∈[1,k]，，即对所有目标函数值，至少与x一样好，如果支配x，它也弱支配x。 如果对所有i∈[1,k]，=， 则与x互相弱支配。用记号

表示 弱支配x。

3.非支配。 称点是非支配的，如果不存在能支配它的x。非劣、允许的，以及有效的，都是非支配的同义词。

4.帕累托最优点。 帕累托最优点，也被称为帕累托点，是不受搜索空间中任意一点x支配的点。即，

5.帕累托最优集。也被称为帕累托集并记为，是所有非支配的的集合。

6.帕累托前沿。也被称为非支配集合，并记为，是相应于帕累托集的所有函数向量f(x)的集合。

注意，是非支配的并不意味着支配所有与不等的x。对所有i∈[1,k]，可能会有 = ，在这种情况下x和互相都是非支配的，其中一个不会支配另一个。还可能出现的情况是，以有两个目标的问题为例，其中并且。在这种情况下x和都是非支配的，其中一个不会支配另一个。

支配

帕累托集这个概念的局限在于它的非此即彼，非黑即白的性质。例如，考虑下面三个费用函数值的集合：

x支配y和z，但是帕累托支配的概念并不考虑支配水平之间的差别，也不会识别在目标函数空间中相互靠的很近的两个候选解。在（11）式中，x支配y，但是因为x和y很相似，相互之间几乎都是非支配的。实际上，差不多也可以说y支配z。由此引出了支配的概念。

1. 加性支配： 称点加性支配x，如果对某个＞0和所有i∈[1,k]， ＜ +。也就是说， “接近”支配x，这里的“接近”有加性参数来量化。
2. 乘性支配： 称点乘性支配x，如果对某个＞0和所有i∈[1,k], ＜ +(1+)。也就是说， “接近”支配x，这里的“接近”有乘性参数来量化。

我们用记号

表示 支配x，注意，如果=0，则支配等价于弱支配。

注意，对于＞0，支配是比弱支配更弱的支配，也就是说，如果 弱支配x，则对＞0， 也支配x。反之，如果对某个＞0， 支配x，则 可能弱支配x，可能不能弱支配x：

---

多目标优化的目标

MOEA可能的一些目标如下：

1. 在与真实帕累托集的某个距离之内找到最多个体；
2. MOEA的近似帕累托集与真实帕累托集之间的平均距离；
3. 在近似帕累托集中找到最具多样性的个体；
4. 目标函数空间中候选解到理想点，也称为乌托邦点的距离最小。

目标1和2是要找出真实帕累托集的“最好的”近似，目标3是要找出解的多样化集合，以便让决策者有足够的资源做出明智的决定。与其他目标不同，目标4是要找出与决策者的理想解尽可能接近的解。

目标1和2假定我们一开始就知道真实帕累托集。如果知道真实的帕累托集，并且MOEA给出一个近似的帕累托集，可以计算它们之间的平均距离M(，)

 其中||·||是用户指定的距离测度。

可以用几种不同的方式度量目标3。首先，可以度量每一个个体与近似帕累托集中离他最近的邻居的平均距离；其次，可以度量在近似帕累托集中两个末端的个体之间的距离；最后，可以计算在帕累托集中与每个元素距离大于某个阈值的个数的平均

其中，是用户指定的距离。一般来说，随着中元素的个数的增加而增大，也随着中元素多样性的增加而增大。

目标4被称为目标向量优化，目标达到，或目标规划。我们通常使用欧氏距离度量目标函数向量f和理想点之间的距离，欧氏距离也被称为二范数距离。f和之间的距离定义如下：

 也可以使用其他距离，如加权二范数，一范数，或无穷范数。

1.超体积

 常用的度量帕累托前沿质量的另一个指标是它的超体积。假设MOEA在近似帕累托前沿中找到M个点={}，j∈[1,M]，其中是一个k维函数。超体积为

对于最小化问题，超体积越小表明帕累托前沿的近似也越好。

 假设有两个MOEA，它们都被用来近似一个有两个目标的最小化问题的帕累托前沿。下图所示为它们的近似帕累托前沿。图a的近似点为

其超体积为1×5+2×3+5×1=16。图b的近似点为

其超体积为1×4+3×3+4×1=17.图a中的比图b中的稍好。 

 不能盲目的将超体积作为衡量帕累托前沿质量的指标。（18）式说明一个空的近似帕累托前沿（M=0）得到S可能的最小值。因此，更精确的度量可能是正规化之后的超体积=/M。但这个量也可能不是近似帕累托前沿的好指标。考虑某个近似帕累托前沿，其正规化后的超体积。现在假设添加一个新的点到中得到。于是有可能让＞。尽管和的唯一不同是，比多了一个点。显然比好，但 ＞ 与我们的直觉不符。 

因此我们得修改超体积这个测度，不是关于目标函数空间的原点来计算超体积，而是关于帕累托前沿之外的参考点来计算。假设要比较Q个帕累托前沿近似，q∈[1,Q]，首先计算参考点向量r=[]，其中

 然后关于参考点计算超体积

其中，M(q)是在第q个近似帕累托前沿中点的个数，是在第q个近似帕累托集中第j个点。参考点超体积S’较大表示最小化问题的帕累托前沿较好。我们可以采用正规化后的参考点超体积

如果要将帕累托点的个数也纳入指标中，也可以采用总的参考点超体积。

2.相对覆盖度

比较近似帕累托前沿的另一种方式是计算在一个近似中的个体被另一个近似中至少一个个体弱支配的平均个数。假设两个近似记为 和 。定义 相对于 中个体被 中至少一个个体弱支配的平均个数：

 

注意，。如果=0，则对没一个个体a2∈  ，在  中没有个体弱支配a2。如果=1，则对每一个个体a2∈  ，在 中至少有一个个体弱支配a2。

---

基于非帕累托的进化算法

接下来讨论几种MOEA，它们并不显示的使用帕累托支配个概念。

1.集结方法

集结方法将MOP的目标函数向量组合成一个目标函数。例如，将（1）式中k个目标的MOP转换为问题

是权重参数的集合，其元素都为正且总和为1。（25）式被称为加权和方法，但也可以采用其他的集结方法。例如，把目标组合成一个乘积：

如果采用该方法，就应该确保对所有的x，目标0。无论用什么方法集结，其重点在于将MOP转化为单目标优化问题。

如果帕累托前沿是凹的，集结方法就无法得到完整的帕累托前沿，我们用下面的例子来说明。

 考虑问题

其中x∈[0,4]，这是一个一维两个目标的MOP，我们可以将两个目标集结成一个标量目标

其中w∈[0,1]。下图为两个问题的解。我们知道帕累托前沿是凹的，集结方法正确地给出了帕累托前沿凸起的部分，但凹进的部分不正确。

 凹帕累托前沿的目标达成

有时候，通过七届下面的问题来近似目标达到：

 其中，是第i个目标的理想解，是权重参数的集合，表示每个目标的相对重要性，每一个都是正数。（33）式允许比用户的理想解还好的解存在。如果最优的α＞0，则不能达到理想点，但（33）式的解是尽可能靠近理想点的向量解。如果最优的α＜0，对于每一个目标，就可以找到比理想解更好的解。

2.向量评价遗传算法

向量评价遗传算法VEGA是最早的MOEA。VEGA每次使用一个目标函数在种群中选择。它给出子种群的集合，每个目标函数一个集合。然后从子种群中选择个体得到下一代的父代，并利用标准进化算法的重组方法让父代组合得到子代。算法1为VEGA的概述。

算法1通常随机生成初始化种群。在每一代计算所有N个个体的全部k个费用函数值。然后用所需的选择方案选择M个个体，即子种群。我们根据概率来选择每个目标函数的子种群。再生成每个目标函数的子种群之后，将它们组合起来得到父代1种群P。然后将P中的个体重组生成子代集合C。可以采用任何一个进化算法进行重组。

在单目标进化算法中实施精英能极大地改善算法性能。在算法1中实施精英的几种方式。例如，在每一代找到针对每一个目标函数的最好个体，并确保它们能留到下一代；或者可以在每一个直到非支配个体，确保其中至少能有几个保留到下一代。

3.字典排序

与VEGA类似，它允许用户对目标按优先级排序。基于优先级的目标对个体做比较执行锦标赛选择。锦标赛选择也可以基于随机的目标。

 算法2概述了字典排序方法。在最初的字典排序方法中，最外层的循环按目标函数的优先级对i∈[1,k]执行。在它的随即便种中，则会一直执行直到满足用户定义的终止准则，并且在每一代指标i会随机的变化。

 4.-约束方法

-约束方法每次最小化一个目标函数，同时将其他目标函数限制在给定的阈值内。首先，对于i∈[1,k]，通过单目标优化算法最小化找到目标函数的最小值。于是得到目标函数约束的下界：

然后最小化第一个目标同时限制其他目标小于某个阈值：

 由（35）式得到的最后的种群作为下一个进化算法的初始种群，最小化下一个目标：

 对所有k个目标重复这个过程，然后减小值并重复顺序最小化的过程。算法3概述约束MOEA。在实施-约束方法时，MOEA最具挑战的是算法3如何精确决定“设为大于的某个数”以及如何“减小，i∈[1,k]”。

 5.基于性别的方法

 基于性别的方法根据对目标函数的评价为每一个个体的分配性别。基于性别的方法还利用被称为档案的第二种群。档案也是非支配个体的一个集合，与精英类似，他能避免丢失最好的个体。

在k个目标MOP基于性别的方法中，有k个不同的性别，每一个相应于不同的目标。我们对每个个体生成数目相同的初始化种群，然后基于从每个性别i选择一个个体。再用选出的个体重组得到子代个体，按照子代表现得最好的目标为子代个体分配性别。在每一代的最后，通常将种群与档案比较并将非支配个体存入档案同时去掉档案中的被支配个体。算法4概述了多目标优化基于性别的方法。

---

基于帕累托进化算法

下面几节讨论直接使用帕累托支配的方法。

1.多目标进化优化器

a.简单多目标进化优化器（simple evolutionary multi-objective optimizer，SEMO）

最初是为二进制优化提出的算法。在SEMO中，一开始我们随机生成个体中群。一开始的种群规模为1，随着算法找到越来越多的非支配解，种群也在长大。在每一代，我们从种群中随机选出一个个体，让它变异生成子代。如果这个子代不被种群支配，就将它加入种群中，并去掉种群中被支配的个体。算法5说明SEMO。

b.多样性多目标进化优化器（divercity evolutionary multi-objective optimizer，DEMO） 

SEMO有一个问题是它的种群会不受限制的生长。我们可以在测试时候将y纳入种群P时采用支配而不是支配来处理这个问题。由此得到多样性多目标进化优化器DEMO。DEMO采用的算法和算法5相同，但它使用支配作为是否将y纳入P的准则。这个准则就是仅当y不被P中的其他个体支配是就将y纳入当前种群。因为支配是比帕累托支配更弱的一种支配。在DEMO中将y纳入种群的准则比在SEMO中更严格。DEMO本质上是将目标空间分成超箱，并且让种群在每个超箱中包含的个体最多只有一个。DEMO通常使用加性支配。

对两个目标的优化问题，如下图说明DEMO的概念。我们不会将子代纳入种群，因为它被同一个超箱中的个体支配，但会将纳入种群因为它不会被当前种群中的任何一个成员支配。注意，下图说的并不是百分百正确，因为DEMO的超箱是相对当前种群定义的。

2.基于的多目标进化算法

-MODE包含一个种群和一个档案。在每一代，我们从种群中选择一个个体并在档案中选择一个个体，用某种重组方法得到一个子代。

如果子代支配种群中的一个个体，就用子代替换被支配的个体。如果子代支配不止一个个体，则替换随机选出的一个个体。

然后将子代与档案比较。这种比较会出现四种情况：

（1）如果子代被归档中的一个个体支配，就不把子代放进档案中。

（2）如果子代支配某个归档个体，则将子代添加到档案，并去掉档案中的被支配个体。

如果这两个条件不成立，就计算子代x的-箱B(x)：对于j∈[1,k]

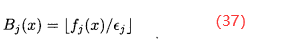
其中，k是目标函数的个数，是第j个目标所需的分辨率。由此得到子代与档案比较的第三种情况：（3）如果子代x与一个归档个体同一个 -箱中，如果子代更接近目标函数的原点，就让子代替换a：

（4）如果上面的三种情况都没有出现，就将子代添加到档案中，档案规模加1。

下图说明了这4种可能性。这里描述的逻辑保证档案的每个-箱中最多只有一个个体。尽管档案从一代到另一代会长大，这个逻辑会限制它的增长。

图（a）说明子代被一个或者多个归档支配；在这种情况下，子代不会被纳入档案。图（b）说明子代支配一个或者多个归档个体；在这种情况下，子代被纳入档案，替换被子代支配的个体；图（c）说明子代和归档个体互相非支配，且子代与归档个体在同一个 -箱中；在这种情况下，如果子代更接近目标函数空间的原点，子代就替换同一个 -箱中归档个体。最后，图（d）说明子代和档案互相都是非支配的，并且子代没有与任何一个归档个体在同一个 -箱中；在这种情况下，子代被添加到档案，档案规模加1.

算法6概述 -MOEA。

3.非支配排序遗传算法NSGA

非支配排序遗传算法（nondominated sorting genetic algrorithm，NSGA），它基于每一个个体的支配水平为其分配费用。首先将所有的个体复制给一个临时种群T。然后找出T中的所有非支配个体；用集合B表示这些非支配个体并未它们分配最低的费用。接下来从T中去掉B并在缩减后的集合T中找出所有非支配个体，为这些个体分配次低的费用。重复这个过程，就得到基于个体非支配水平的每一个个体的费用。算法7概述NSGA。

NSGAⅡ

 NSGAⅡ是对NSGA的改进。 NSGAⅡ在计算个体x费用时不仅考虑支配它的个体而且还考虑它支配的个体。对每一个个体，沿着目标函数的维度找出离它最近的个体，并用它们之间的距离计算拥挤距离。 NSGAⅡ不适用档案，但使用(μ+λ)进化策略实施精英。

 NSGA将每一个个体x的拥挤距离设置为沿每个目标函数的维度距离它最近的邻居的平均距离。加入，在 NSGA中有N个个体，进一步假设x的目标函数向量为

对于每个目标的维度，找出种群中离得最近的较大值和离得最近的较小值，如下：

然后计算x的拥挤距离：

在目标函数空间中较拥挤的地方拥挤距离往往较小。位于目标函数空间极值处的个体的距离会无穷大：

最大立方体的边界不会超出x的最近邻居在每个维度上目标函数空间的坐标，拥挤距离应该相应于最大立方体的边长的一半。下图显示二维目标函数空间中的一个超立方，它是一个矩形。下图中x在方向上的最近邻居是A和C，在方向上的最近邻居是A和B。

最大超立方体（在二维空间中是一个矩形）的周长的1一半为x的拥挤距离，最大立方体的边界不会超出x的最近邻居在目标函数空间中的坐标。 

既然种群中的每个个体都由一个拥挤距离，我们就把它作为次级排序的参数得到每一个个体的排名。与NSGA算法一样，我们基于非支配水平对每一个个体排序，同时还包含基于拥挤距离的一个细粒度的排名水平。也就是说，如果，或者如果=且d(x)>d(y)，则x的排名比y的好。NSGA算法采用选择重组父代，而NSGAⅡ则用上述的排名来选择重组父代。

4.多目标遗传算法 

它基于支配水平分配费用。MOGA从相反的方向解决费用分配。MOGA基于有多少个个体支配x来为他分配费用。我们对所有非支配个体分配相同的费用。对每个被支配个体x，则根据有多少个个体支配它以及有多少个个体在它附近来分配费用。与NSGAⅡ使用拥挤距离类似，这样做会促进种群的多样性。

在MOGA中，x的排名比y好（即），如果种群P中支配它的个体较少（即d(x)＜d(y)），或者支配它们的个体数相同且在目标函数空间靠近x的个体比靠近y的个体少（即s(x)＜s(y)）。这个排名的方法可以表示为

 其中，是用户定义的参数，||·||是某个距离测度，可以自动的实现共享，这样就不需要其他用户定义共享参数。算法8概述MOGA。

5.小生境帕累托遗传算法NPGA

小生境帕累托遗传算法（NPGA）与NSGA和MOGA类似，它基于支配水平分配费用。NPGA试图减少NSGA和MOGA的计算量。我们从种群中随机选出两个个体和，然后随机选出种群的一个子集S，这个子集通常约占种群的10%。如果其中有一个个体或被S中的某个个体支配，另一不被支配，则记非支配个体为r（r为或中的一个），它赢得锦标赛被选出来进行重组。如果和这两个个体都被S中至少一个个体支配，或都不被S中的任何一个个体支配，则用适应度分享来决定锦标赛的赢家；也就是说，处于目标函数空间中不拥挤区域中的个体赢得锦标赛。这个选择过程可以描述如下：

 是支配个个体数，是的拥挤距离，r是我们最后选出来重组的个体（ 或 ）。

搜索空间或目标函数空间中越拥挤的区域个体的拥挤距离越小。在NPGA中使用拥挤距离会鼓励多样性；它特别适合多模态问题，或者用户有意在函数空间或搜索空间中相距很远的区域找到好的潜在解的那些问题。算法9概述NPGA。

6.优势帕累托进化算法SPEA

优势帕累托进化算法（strength Pareto evolutionary algorithm，SPEA）是第一个显式地利用精英的MOEA。精英通常是单目标和多目标进化算法的一个常识性的选择。如果基于用户的偏好的方法用与MOEA，并且让偏好随时间地变化而变化，精英可能会导致性能退化。

SPEA会把在学习过程中找到的所有非支配个体留在档案中。每当找到非支配个体就把它复制到档案中。对每个归档个体α，基于种群中被α支配的个体数为其分配优势值S(α)：

其中，P是候选解的集合，N为P的大小，A是档案的集合。注意， S(α)∈[0,1）。对P中的每一个个体x，我们找出支配它的的所有归档个体的集合α(x)。然后令x的原始费用为α(x)中优势个体的总和，记为R(x)：

在上面的等式加上1能保证R(x)≥1，它反过来保证，对所有x∈P和所有α∈A，R(x)＞S(α)。注意，如果x的原始费用很低，则x是一个高性能个体。

下图说明优势和原始费用的计算，其中档案规模为|A|=3种群规模|P|=6。下图显示帕累托前沿的优势值为它们所支配的个体数正规化后的值。此图也显示每个被支配的点的原始费用为支配它的帕累托前沿点的优势的总和再加上1。注意，个体越远离帕累托前沿（即当个体被更多的帕累托前沿支配），原始费用就越大。

帕累托前沿个体用x表示，旁边显示的是它们的优势值，非帕累托前沿用实心圆表示，旁边显示的是它们的原始费用。例如9/7的点被优势值为2/7的点支配，因此原始费用为2/7+1=9/7。

 在每一代将{P，A}中的非支配个体都加入到档案A中，但这会让档案无限增长。SPEA用聚类来处理这个潜在的问题。如果档案中有|A|个个体，我们一开始定义一个个体为一个聚类。然后把两个离得最近的聚类合并为一个聚类，A的聚类个数减1.重复这个过程直到档案中含有个聚类，它是我们想要的档案规模。最后，在每一个聚类中留下一个点，通常是离聚类中心点最近的那个点。

SPEA2

SPEA2对SPEA做了医学改进。首先，我们不仅为档案个体分配优势值S(α)，也为种群中的个体分配优势值：

 与（45）式比较，可知上式没有对优势值做归一化处理。

其次，在计算P中每个个体的原始费用时也稍微有点不同，我们将种群和档案中支配个体的总优势和起来：

 与（46）式比较，上式在计算原始费用时没有加1。

再次，基于邻近个体数修改每个x∈P的原始费用；也就是说，对于目标函数空间中邻居较多的个体在费用上给予惩罚。对于y≠x的所有x∈P和所有y∈{P,A}，找出f(x)和f(y)之间的距离来惩罚。通常采用欧氏距离。对于每一个x∈P，将它与每一个y∈{P,A}之间的距离按升序排列，得到x的（|P|+|A|）个元素的有序距离列表。然后选择距离列表中的第j个元素，它是x和距它第j个最近邻居之间的距离，记为。定义x的密度为

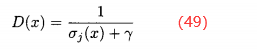
 这列分母需要选择常数γ以保证D(x)<1。

最后，将原始费用加到密度上得到修改后x点的费用：

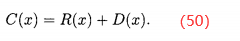
 由（48）式可知，所有非支配个体的原始费用为0，并且对于所有x，D(x)<1，因此所欲非支配个体的费用C(x)<1。

在SPEA中档案规模没有下界，但在SPEA2中档案规模保持为一个常值。如果在SPEA2过程中任一点档案规模过小，就将种群中费用最低的个体，即使它们是被支配的，纳入档案直到档案规模达到最想要的值。如果档案规模过大，就在目标函数空间中通过找出距每个x∈A最近的邻居：

 由此得到|A|个的值，这里|A|为档案的规模。下面我们用D表示具有最小的个体的集合：

D中至少会有两个个体，因为两个个体x和y之间的距离与y与x之间的距离相同。在D中的所有个体中，找出距不属于D的任一归档个体最近的个体，记为：

 从档案中去掉，这样档案规模减1。如果|A|过大，重复上述过程，在每次迭代中去掉一个个体，直到达到想要的档案规模。

算法10概述了SPEA和SPEA2个基本思想。

7.帕累托归档进化策略PAES

帕累托归档进化策略PAES，其动机来自（1+1）进化策略。在每一代，单个个体利用变异生成单个子代。在每一代一个父代生成一个子代，如果子代不被档案中的个体支配就将它纳入档案。如果档案规模超过某个阈值，就通过剔除拥挤距离最小的个体（即在搜索空间或目标函数看空间中最拥挤的个体）修剪档案。算法11概述一般的PAES。s(α)是α的拥挤距离，对于目标函数空间或搜索域的拥挤区域中的个体数。

---

基于生物地理学的多目标优化

1.向量评价BBO

因为BBO以迁移为基础，多目标BBO的迁入以每一个个体的第个目标函数值为基础，这里是在第i个迁移实验的随机目标函数的指标，然后，让迁出以每一个个体的第个目标函数值为基础，这里也是一个随机目标函数指标。由此得到向量评价BBO（VEBBO）算法12。

2.非支配排序BBO

将BBO与NSGA结合，算法7是NSGA。为了针对BBO修改算法7，只需要将重组语句改为一个BBO的迁移操作。由此得到非支配排序BBO算法（NSBBO），算法13。

3.小生境帕累托BBO

与NSBBO算法类似，为了针对BBO修改算法9，只需要把重组语句改为BBO的迁移操作。因为NPGA已经基于非支配选择了R中的个体，我们可以简单的对R中的每一个个体以相等的迁移概率选择迁移操作。由此得到小生境帕累托BBO（NPBBO）算法14。

4.优势帕累托BBO

BBO与SPEA或SPEA2结合的方法，算法10是SPEA和SPEA2，为了针对BBO修改算法10，需要改变选择父代和重组方法的语句。用SPEA或者SPEA2的费用来计算迁移率，然后利用这些迁移率实施BBO。从种群P和档案A中选出父代，这就是优势帕累托BBO(SPBBP)算法15。