代码随想录算法训练营第day39|62.不同路径 、 63. 不同路径 II

目录

a.62.不同路径 

b. 63. 不同路径 II 

---

 

a.62.不同路径 

题目链接

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

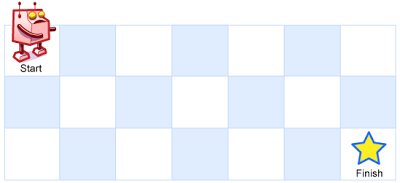
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

思路：只能往下或者往右走，那么对于点（i,j)，只能由其上边位置（i-1,j)往下一步或者左边位置（i,j-1)往右一步；

        

按照动规五部曲来分析：

1.确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2.确定递推公式

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

3.dp数组的初始化

如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。

所以初始化代码为：

for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

4.确定遍历顺序

这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。

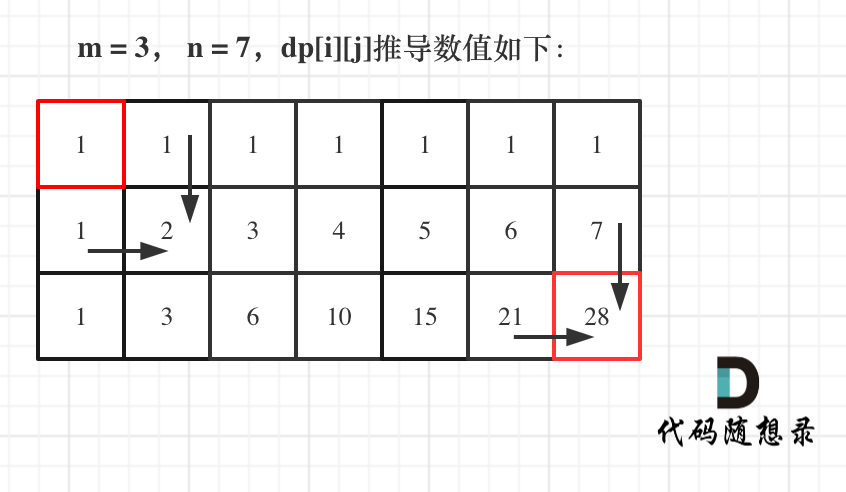
5.举例推导dp数组

如图所示：

        

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>>dp(m,vector<int>(n,0));
        //从（0，0）出发到第一行或者第一列上的格子只有一种路径
        for(int i=0;i<m;i++) dp[i][0]=1;
        for(int j=0;j<n;j++) dp[0][j]=1;
 
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
                
            }
        }
        return dp[m-1][n-1];
    }
};

b. 63. 不同路径 II 

题目链接

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

思路：障碍物区域无法行进，相当于从该处移动到其他地方的路径是0条，推导dp数组时遇到障碍物直接跳过更新就好；需要注意的是初始化dp的时候，对于第0行和第0列，如果·出现了障碍物，那么按照dp数组的定义，从原点出发到第0行/列的障碍物之后的格子的路径应该全为0（因为过不去了）

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m,vector(n,0));
        //第0行和第0列障碍物之前的位置才初始化为1
        for (int i = 0; i < m &&obstacleGrid[i][0] == 0 ; i++) dp[i][0]=1;
        for (int j = 0; j < n &&obstacleGrid[0][j] == 0 ; j++) dp[0][j]=1;
        for (int i = 1; i < m ; i++) {
            for (int j = 1; j < n  ; j++){
                if(obstacleGrid[i][j]==1) continue;//遇到障碍物，跳过推导
                dp[i][j] = dp[i-1][j] + dp[i][j-1];//没有障碍物时，正常推导
 
 
            }
        }
        return dp[m-1][n-1];
        
        
    
    }
};

参考：代码随想录 (programmercarl.com)