视觉SLAM--直接法_视觉slam直接法

直接法(摘抄于高翔博士的《视觉SLAM十四讲》)

8.4.1直接法的推导

如图8-3所示，

考虑某个空间点P和两个时刻的相机。P的世界坐标为[X，Y，Z]，它在两个相机上成像，记非齐次像素坐标为，。我们的目标是求第一个相机到第二个相机的相对位姿变换。我们以第一个相机为参照系，设第二个相机旋转和平移为R，t（对应李代数为ξ ）。同时，两相机的内参相同，记为K。为清楚起见，我们列写完整的投影方程：

其中是P的深度，是P在第二个相机坐标系下的深度，也就是RP+t的第三个坐标值。由于只能和齐次坐标相乘，所以我们乘完之后要取出前三个元素。这和上一讲以及相机模型部分的内容是一致的。

回忆特征点法中，由于我们通过匹配描述子，知道了，的像素位置，所以可以计算重投影的位置。但在直接法中，由于没有特征匹配，我们无从知道哪一个与对应着同一个点。直接法的思路是根据当前相机的位姿估计值，来寻找的位置。但若相机位姿不够好，的外观和会有明显差别。于是，为了减小这个差别，我们优化相机的位姿，来寻找与更相似的。这同样可以通过解一个优化问题，但此时最小化的不是重投影误差，而是光度误差（Photometric Error），也就是P的两个像的亮度误差：

注意这里e是一个标量，所以没有加粗。同样的，优化目标为该误差的二范数，暂时取不加权的形式，为：

能够做这种优化的理由，仍是基于灰度不变假设。在直接法中，我们假设一个空间点在各个视角下，成像的灰度是不变的。我们有许多个（比如N个）空间点，那么，整个相机位姿估计问题变为：

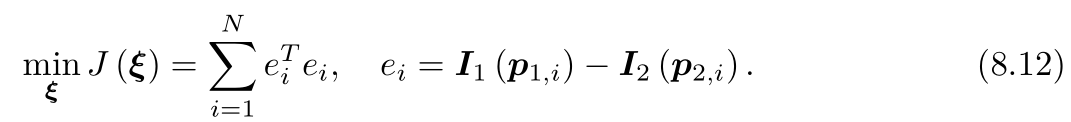
注意这里的优化变量是相机位姿ξ 。为了求解这个优化问题，我们关心误差e是如何随着相机位姿变化的，需要分析它们的导数关系。因此，使用李代数上的扰动模型。我们给exp⁡(ξ) 左乘一个小扰动exp⁡(δξ) ，得：

类似于上一章，记

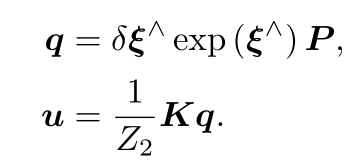
这里的q为P在扰动之后，位于第二个相机坐标系下的坐标，而u为它的像素坐标。利用一阶泰勒展开，有：

我们看到，一阶导数由于链式法则分成了三项，而这三项都是容易计算的：

1.为u 处的像素梯度；

2. 为投影方程关于相机坐标系下的三维点的导数。记,根据上一节的推导，导数为：

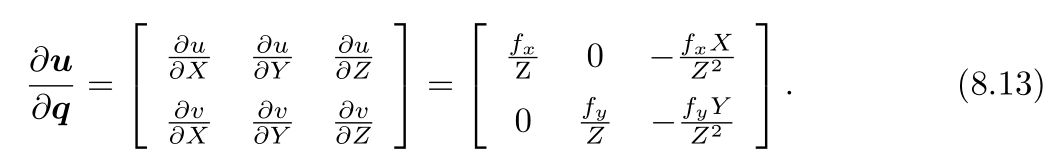
3. 为变换后的三维点对变换的导数，这在李代数章节已经介绍过了：

在实践中，由于后两项只与三维点q有关，而与图像无关，我们经常把它合并在一起：

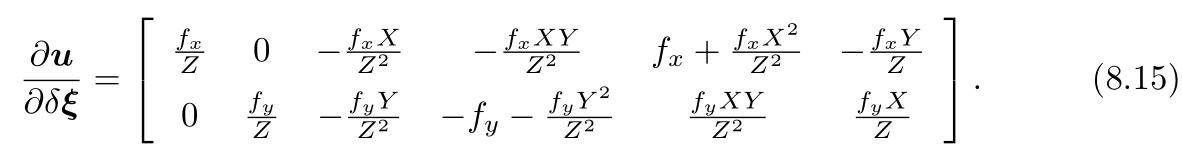
这个2×6的矩阵在上一讲中也出现过。于是，我们推导了误差相对于李代数的雅可比矩阵：

对于N个点的问题，我们可以用这种方法计算优化问题的雅可比，然后使用G-N或L-M计算增量，迭代求解。至此，我们推导了直接法估计相机位姿的整个流程，下面我们通过程序来演示一下直接法是如何使用的。

8.4.2直接法的讨论

在我们上面的推导中，P是一个已知位置的空间点，它是怎么来的呢？在RGB-D相机下，我们可以把任意像素反投影到三维空间，然后投影到下一个图像中。如果在单目相机中，这件事情要更为困难，因为我们还需考虑由P的深度带来的不确定性。现在我们先来考虑简单的情况，即P深度已知的情况。

根据P的来源，我们可以把直接法进行分类：

1. P来自于稀疏关键点，我们称之为稀疏直接法。通常我们使用数百个至上千个关键点，并且像L-K光流那样，假设它周围像素也是不变的。这种稀疏直接法不必计算描述子，并且只使用数百个像素，因此速度最快，但只能计算稀疏的重构。

2. P来自部分像素。我们看到式（8.16）中，如果像素梯度为零，整一项雅可比就为零，不会对计算运动增量有任何贡献。因此，可以考虑只使用带有梯度的像素点，舍弃像素梯度不明显的地方。这称之为半稠密（Semi-Dense）的直接法，可以重构一个半稠密结构。

3. P为所有像素，称为稠密直接法。稠密重构需要计算所有像素（一般几十万至几百万个），因此多数不能在现有的CPU上实时计算，需要GPU的加速。但是，如前面所讨论的，梯度不明显的点，在运动估计中不会有太大贡献，在重构时也会难以估计位置。

可以看到，从稀疏到稠密重构，都可以用直接法来计算。它们的计算量是逐渐增长的。稀疏方法可以快速地求解相机位姿，而稠密方法可以建立完整地图。具体使用哪种方法，需要视机器人的应用环境而定。特别地，在低端的计算平台上，稀疏直接法可以做到非常快速的效果，适用于实时性较高且计算资源有限的场合。