- 1一文详解多模态大模型发展及高频因子计算加速GPU算力 | 英伟达显卡被限,华为如何力挽狂澜?_dalle重塑技术
- 2GPT-4劲敌Claude 3来了,上下文和多模态显著提升:OpenAI是可被超越的
- 3【吴恩达】prompt engineering(原则 迭代 文本概括 推断、订餐机器人)
- 4Docker 操作mongo_docker exec -it mongo mongo admin
- 5pycharm无法识别conda环境(已解决)_pycharm检索不到虚拟环境
- 6【自然语言处理】【知识图谱】知识图谱表示学习(一):TransE、TransH、TransR、CTransR、TransD
- 7AI大模型学习:理论、实践与未来展望_ai大模型技术进展学习心得
- 8DevOps生命周期的基本指南
- 9使用vscode编写、运行Python程序_vscode运行python
- 10nltk.download()报错getaddrinfo failed_nlgetaddrinfo failed
数据结构习题:找出临界点之间的最小和最大距离_数据关联最小距离例题
赞
踩
找出临界点之间的最小和最大距离
时间限制: 1S 类别: DS:数组与链表->链表--较难
问题描述 :
链表中的 临界点 定义为一个 局部极大值点 或 局部极小值点 。
如果当前节点的值 严格大于 前一个节点和后一个节点,那么这个节点就是一个 局部极大值点 。
如果当前节点的值 严格小于 前一个节点和后一个节点,那么这个节点就是一个 局部极小值点 。
注意:节点只有在同时存在前一个节点和后一个节点的情况下,才能成为一个 局部极大值点 / 极小值点 。
给你一个链表 head ,返回一个长度为 2 的数组 [minDistance, maxDistance] ,其中 minDistance 是任意两个不同临界点之间的最小距离,maxDistance 是任意两个不同临界点之间的最大距离。如果临界点少于两个,则返回 [-1,-1] 。
输出minDistance和maxDistance的值。
示例 1:
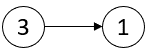
输入:head = [3,1] 输出:[-1,-1] 解释:链表 [3,1] 中不存在临界点。
示例 2:

输入:head = [5,3,1,2,5,1,2]
输出:[1,3]
解释:存在三个临界点:
- [5,3,1,2,5,1,2]:第三个节点是一个局部极小值点,因为 1 比 3 和 2 小。
- [5,3,1,2,5,1,2]:第五个节点是一个局部极大值点,因为 5 比 2 和 1 大。
- [5,3,1,2,5,1,2]:第六个节点是一个局部极小值点,因为 1 比 5 和 2 小。
第五个节点和第六个节点之间距离最小。minDistance = 6 - 5 = 1 。
第三个节点和第六个节点之间距离最大。maxDistance = 6 - 3 = 3 。
示例 3:
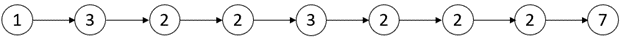
输入:head = [1,3,2,2,3,2,2,2,7]
输出:[3,3]
解释:存在两个临界点:
- [1,3,2,2,3,2,2,2,7]:第二个节点是一个局部极大值点,因为 3 比 1 和 2 大。
- [1,3,2,2,3,2,2,2,7]:第五个节点是一个局部极大值点,因为 3 比 2 和 2 大。
最小和最大距离都存在于第二个节点和第五个节点之间。
因此,minDistance 和 maxDistance 是 5 - 2 = 3 。
注意,最后一个节点不算一个局部极大值点,因为它之后就没有节点了。
提示:
链表中节点的数量在范围 [2, 10^5] 内
1 <= Node.val <= 10^5
输入说明 :
输入链表长度n,然后输入n个整数,每个整数在1到10^5之间,以空格分隔。
n在范围 [2, 10^5] 内
输出说明 :
输出两个整数,以空格分隔。
输入范例 :
9
1 3 2 2 3 2 2 2 7
输出范例 :
3 3
思路分析:
先找到所有临界点,再处理最大/小距离。
由于需要临界点在链表中序号算出距离,故在节点的数据域中设置一个变量存储节点的序号(不是下标)。若某节点是临界点,则将其序号存储到数组中(此处用vector<long> 动态数组)。找完临界点后,vector 中的最后一个元素减第一个元素的值即最大距离。最小距离只可能在某临界点与其左右临界点(若存在)之间产生,若先将最小距离设置成最大距离,从vector 前面开始遍历,只需要判断某临界点的序号与后一序号的差值绝对值与当前最小距离的大小即可。若其比当前最小距离小,则将其设置为新的最小距离。
时间复杂度T(n)=O(n) 。
- #include<iostream>
- #include<vector>
- using namespace std;
- typedef struct ListNode
- {
- long data;
- long no; //存储节点序号
- ListNode *prior=NULL; //用双向链表
- ListNode *next=NULL;
- }*LinkList;
-
- bool isCriticalPoint(ListNode *p)
- { //判断某节点是否是临界点
- if((p->data)<(p->prior->data)&&(p->data)<(p->next->data))
- return true;
- else if((p->data)>(p->prior->data)&&(p->data)>(p->next->data))
- return true;
- return false;
- } //isCriticalPoint
-
- LinkList CreateDoubleList_Tail()
- { //尾插法创建双向链表(无头节点)
- LinkList head;
- ListNode *p, *rear;
- long n, data;
-
- cin>>n;
- for(int i=0;i<n;i++)
- {
- cin>>data;
- p=new ListNode;
- p->data=data;
-
- if(i==0)
- head=rear=p;
- else
- {
- p->prior=rear;
- rear->next=p;
- rear=p;
- p->no=i+1; //对新节点编号
- }
- }
- return head;
- } //CreateDoubleList_Tail
-
- void PrintDistance(LinkList head)
- {
- long distance[2]; //0: min, 1: max
- ListNode *p=head->next; //直接从第二个节点开始
- vector<long> v; //存储临界节点的序号
-
- //找临界节点的序号
- while(p->next) //由于n>=2,故p->prior 肯定存在,只需保证p->next 存在即可
- {
- if(isCriticalPoint(p))
- v.push_back(p->no);
- p=p->next;
- }
-
- //找临界节点的最大、小距离
- if(v.size()==0||v.size()==1) //特殊处理
- {
- cout<<-1<<' '<<-1;
- return ;
- }
- //最大距离
- distance[1]=v.back()-v.front(); //注意,谁减谁
- //最小距离
- distance[0]=distance[1]; //为最小距离赋初值
- for(auto it=v.begin();it<v.end();it++)
- {
- if(it<v.end()-1&&(*(it+1)-*it)<distance[0]) //it<v.end()-1为了保证*(it+1)存在
- distance[0]=*(it+1)-*it;
- }
- cout<<distance[0]<<' '<<distance[1];
- } //PrintDistance
-
- int main()
- {
- LinkList head=CreateDoubleList_Tail();
-
- PrintDistance(head);
- return 0;
- }




