LPA算法原理_lpa线性检测原理

作者：笔触狂放9 | 2024-03-30 04:37:17

踩

lpa线性检测原理

LPA算法学习记录

算法原理

算法原理

标签传播算法作为一种直推式学习方法，其被应用到了小样本学习中，以试图解决数据量过少的问题。本文主要阐述最简单的LPA原理

构建完全图(W矩阵)

W矩阵是一个N * N的矩阵，由它代表完全图，很明显，这是一个对称的方阵，N表示结点数量。 $w_{ij}$ 表示结点 $N_j$ 与 $N_i$ 之间的相似度。相似度计算公式为：
$w_{\mathrm{ij}}=\exp \left(-\frac{\mathrm{d}_{\mathrm{ij}}}{\sigma^2}\right)=\exp \left(-\frac{\sum_{\mathrm{d}=1}^{\mathrm{D}}\left(\mathrm{x}_{\mathrm{i}}^{\mathrm{d}}-\mathrm{x}_{\mathrm{j}}^{\mathrm{d}}\right)}{\sigma^2}\right)$
在代码实现过程中， $d_{ij}$ 采用的是欧式距离， $\sigma$ 是一个超参数。

概率传播矩阵(P矩阵)

标签传播，重点在于传播，一个结点与其余结点都有连接，都会被其他的结点所影响，但是根据 $w_{ij}$ 的不同，其影响程度也不同，因此P矩阵实际上是W矩阵按行归一化的结果。即相似度越高，影响权重越大。这里给到一个从W转为P的示例：
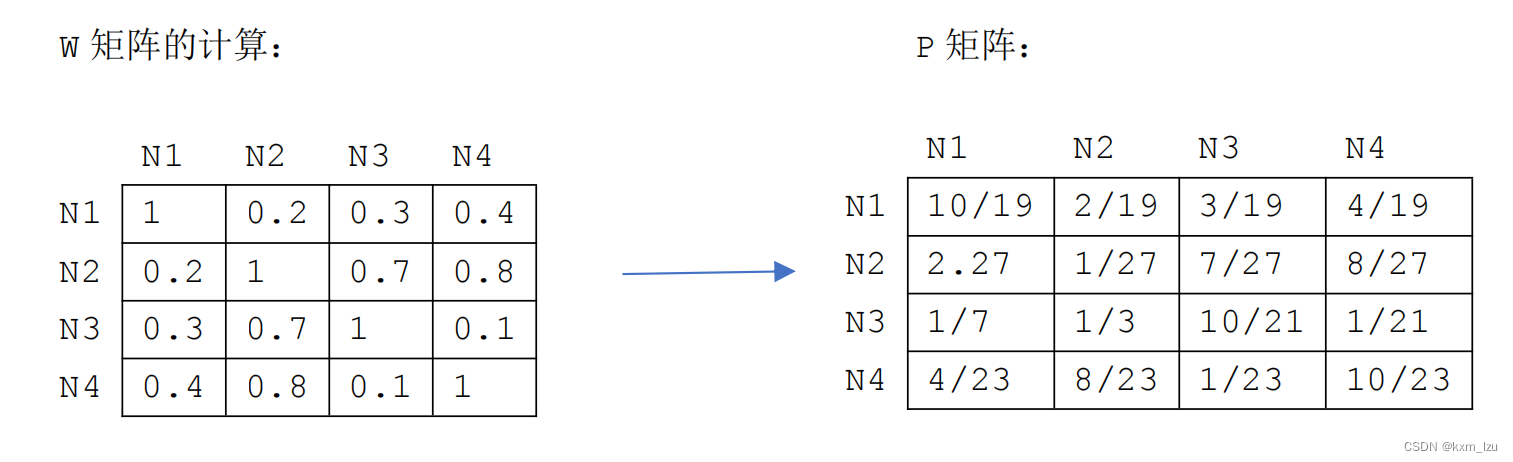
P矩阵的生成
当数据确定后，结点之间的相似度也就确定了，因此P矩阵在整个计算过程中都不会发生改变。

标签矩阵(F矩阵)

在我看来，这实际上就是一个概率矩阵，行代表样本，列代表类别， $F{ij}$ 代表样本 $i$ 属于类 $j$ 的概率。在经过不断迭代使其收敛后，根据概率大小判断样本类别，示例如下图:
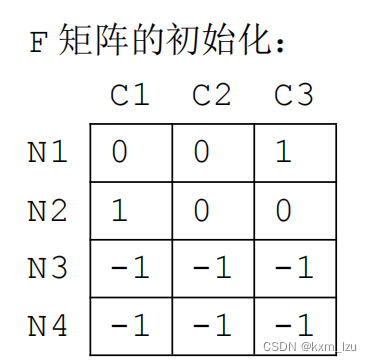
在这里插入图片描述

图中N1,N2代表标记数据，N3,N4代表未标记数据。由于标记数据的标签是确定的，所以其概率设为1，其他类别概率为0。比如图中N1属于C3类，则其值为1，其余为0，N2同理。未标记数据的概率则无所谓了，反正都要迭代生成，不影响结果。

迭代过程

迭代过程就是所谓的”传播过程“，其旨在不断更新F矩阵，使其收敛。因此计算公式很简单：F = P * F。 但是在每次迭代后，要将标记数据的标签重置回来，因为他们的标签是确定的。

python代码实现：

import numpy as np
import math
import matplotlib.pyplot as plt





def buildGraph(MatX, rbf_sigma=None):
    """
    构建完全图，方阵，行列大小均为结点数量
    每个元素按照定义初始化
    :param MatX: 全体数据矩阵
    :param rbf_sigma: 计算公式里的参数
    :return: 返回矩阵P
    """
    num_samples = MatX.shape[0]
    affinity_matrix = np.zeros((num_samples, num_samples), np.float32)
    if rbf_sigma == None:
        raise ValueError("rbf_sigma can't be None!")
    for i in range(num_samples):
        row_sum = 0.0
        for j in range(num_samples):
            diff = MatX[i, :] - MatX[j, :]
            affinity_matrix[i][j] = np.exp(sum(diff ** 2) / (-2.0 * rbf_sigma ** 2))
            row_sum += affinity_matrix[i][j]
        affinity_matrix[i][:] /= row_sum
    return affinity_matrix


def native_knn(dataset, query, k):
    num_samples = dataset.shape[0]

    diff = np.tile(query, (num_samples, 1)) - dataset
    square_diff = diff ** 2
    square_distance = np.sum(square_diff, axis=1)
    sorted_indexs = np.argsort(square_distance)
    if k > num_samples:
        k = num_samples
    return sorted_indexs[0:k]

def build_graph_knn(mat_x, k=None):
    if k is None:
        raise ValueError("k is NULL!")
    num_samples = mat_x.shape[0]
    affinity_matrix = np.zeros((num_samples, num_samples), np.float32)
    for i in range(num_samples):
        k_neighbors = native_knn(mat_x, mat_x[i,:], k)
        affinity_matrix[i][k_neighbors] = 1.0 / k
    return affinity_matrix

def labelPropagation(Mat_Label, Mat_Unlabel, labels, rbf_sigma=1.5, max_iter=500, tol=1e-3):
    """
    :param Mat_Label: 标记的数据
    :param Mat_Unlabel: 没有标记的数据
    :param labels: 所有数据的标签，长度为结点数量
    :param rbf_sigma: 计算公式里的参数
    :param max_iter: 最大迭代次数
    :param tol: 最小误差
    :return: 直接返回未标记数据的标签
    """
    num_label_samples = Mat_Label.shape[0]
    num_unlabel_samples = Mat_Unlabel.shape[0]
    num_samples = num_label_samples + num_unlabel_samples
    labels_list = np.unique(labels)
    num_classes = len(labels_list)  # 得到F矩阵的列数，就是种类的个数

    Mat_X = np.vstack((Mat_Label, Mat_Unlabel))  # 将两个数据矩阵按行堆叠，得到所有的数据
    clamp_data_label = np.zeros((num_label_samples, num_classes), np.float32) # 对于已标记数据的标签矩阵的初始化
    for i in range(num_label_samples):
        clamp_data_label[i][labels[i]] = 1.0   # 属于哪个类，则哪个类对应的列的位置置为1
    label_function = np.zeros((num_samples, num_classes), np.float32) # 初始化总体的F矩阵
    label_function[0: num_label_samples][:] = clamp_data_label # 将已标记数据初始化
    label_function[num_label_samples:num_samples] = -1 # 将未标记数据的标签随便初始化

    affinity_matrix = buildGraph(Mat_X, rbf_sigma) # 首先得到P矩阵

    iter = 0
    pre_label_function = np.zeros((num_samples, num_classes), np.float32) # 每次迭代都会产生预测结果，这个用于记录上一次的label_function
    changed = np.abs(pre_label_function - label_function).sum()
    while iter < max_iter and changed > tol:
        print("---> Iteration %d/%d, changed:%f" % (iter, max_iter, changed))

        pre_label_function = label_function
        iter += 1

        label_function = np.dot(affinity_matrix, label_function) # 按照公式计算
       # label_function = np.vstack((clamp_data_label,label_function[num_label_samples]))
        label_function[:num_label_samples] = clamp_data_label  # 每次都需要将标签数据从新赋为初始的标签，这个是不可以变的
        changed = np.abs(pre_label_function - label_function).sum() # 计算迭代前后的一个损失

    unlabel_data_labels = np.zeros(num_unlabel_samples) # 初始化未标记数据的预测标签
    for i in range(num_unlabel_samples):
        unlabel_data_labels[i] = np.argmax(label_function[i + num_label_samples]) # 最终得到的标记矩阵，每一行是该数据属于哪个类的概率分布，取最大的为预测值

    return unlabel_data_labels


def labelPropagation_knn(Mat_Label, Mat_Unlabel, labels, k=10, max_iter=500, tol=1e-3):
    """
    :param Mat_Label: 标记的数据
    :param Mat_Unlabel: 没有标记的数据
    :param labels: 所有数据的标签，长度为结点数量
    :param rbf_sigma: 计算公式里的参数
    :param max_iter: 最大迭代次数
    :param tol: 最小误差
    :return: 直接返回未标记数据的标签
    """
    num_label_samples = Mat_Label.shape[0]
    num_unlabel_samples = Mat_Unlabel.shape[0]
    num_samples = num_label_samples + num_unlabel_samples
    labels_list = np.unique(labels)
    num_classes = len(labels_list)  # 得到F矩阵的列数，就是种类的个数

    Mat_X = np.vstack((Mat_Label, Mat_Unlabel))  # 将两个数据矩阵按行堆叠，得到所有的数据
    clamp_data_label = np.zeros((num_label_samples, num_classes), np.float32) # 对于已标记数据的标签矩阵的初始化
    for i in range(num_label_samples):
        clamp_data_label[i][labels[i]] = 1.0   # 属于哪个类，则哪个类对应的列的位置置为1
    label_function = np.zeros((num_samples, num_classes), np.float32) # 初始化总体的F矩阵
    label_function[0: num_label_samples][:] = clamp_data_label # 将已标记数据初始化
    label_function[num_label_samples:num_samples] = -1 # 将未标记数据的标签随便初始化

    affinity_matrix = build_graph_knn(Mat_X, k) # 首先得到P矩阵

    iter = 0
    pre_label_function = np.zeros((num_samples, num_classes), np.float32) # 每次迭代都会产生预测结果，这个用于记录上一次的label_function
    changed = np.abs(pre_label_function - label_function).sum()
    while iter < max_iter and changed > tol:
        print("---> Iteration %d/%d, changed:%f" % (iter, max_iter, changed))

        pre_label_function = label_function
        iter += 1

        label_function = np.dot(affinity_matrix, label_function) # 按照公式计算
       # label_function = np.vstack((clamp_data_label,label_function[num_label_samples]))
        label_function[:num_label_samples] = clamp_data_label  # 每次都需要将标签数据从新赋为初始的标签，这个是不可以变的
        changed = np.abs(pre_label_function - label_function).sum() # 计算迭代前后的一个损失

    unlabel_data_labels = np.zeros(num_unlabel_samples) # 初始化未标记数据的预测标签
    for i in range(num_unlabel_samples):
        unlabel_data_labels[i] = np.argmax(label_function[i + num_label_samples]) # 最终得到的标记矩阵，每一行是该数据属于哪个类的概率分布，取最大的为预测值

    return unlabel_data_labels


def show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels):
    for i in range(Mat_Label.shape[0]):
        if int(labels[i]) == 0:
            plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dr')
        elif int(labels[i]) == 1:
            plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Db')
        else:
            plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dy')

    for i in range(Mat_Unlabel.shape[0]):
        if int(unlabel_data_labels[i]) == 0:
            plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'or')
        elif int(unlabel_data_labels[i]) == 1:
            plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'ob')
        else:
            plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'oy')

    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.xlim(0.0, 12.)
    plt.ylim(0.0, 12.)
    plt.show()


def loadCircleData(num_data):
    center = np.array([5.0, 5.0])
    radiu_inner = 2
    radiu_outer = 4
    num_inner = num_data // 3
    num_outer = num_data - num_inner

    data = []
    theta = 0.0
    for i in range(num_inner):
        pho = (theta % 360) * math.pi / 180
        tmp = np.zeros(2, np.float32)
        tmp[0] = radiu_inner * math.cos(pho) + np.random.rand(1) + center[0]
        tmp[1] = radiu_inner * math.sin(pho) + np.random.rand(1) + center[1]
        data.append(tmp)
        theta += 2

    theta = 0.0
    for i in range(num_outer):
        pho = (theta % 360) * math.pi / 180
        tmp = np.zeros(2, np.float32)
        tmp[0] = radiu_outer * math.cos(pho) + np.random.rand(1) + center[0]
        tmp[1] = radiu_outer * math.sin(pho) + np.random.rand(1) + center[1]
        data.append(tmp)
        theta += 1

    Mat_Label = np.zeros((2, 2), np.float32)
    Mat_Label[0] = center + np.array([-radiu_inner + 0.5, 0])
    Mat_Label[1] = center + np.array([-radiu_outer + 0.5, 0])
    labels = [0, 1]
    Mat_Unlabel = np.vstack(data)
    return Mat_Label, labels, Mat_Unlabel

if __name__ == "__main__":
    num_unlabel_samples = 800
    # Mat_Label, labels, Mat_Unlabel = loadBandData(num_unlabel_samples)
    Mat_Label, labels, Mat_Unlabel = loadCircleData(num_unlabel_samples)
    unlabel_data_labels = labelPropagation_knn(Mat_Label, Mat_Unlabel, labels, max_iter=300,k=10)
    show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208

使用KNN建图的方式，结果如下图：
iter=0:
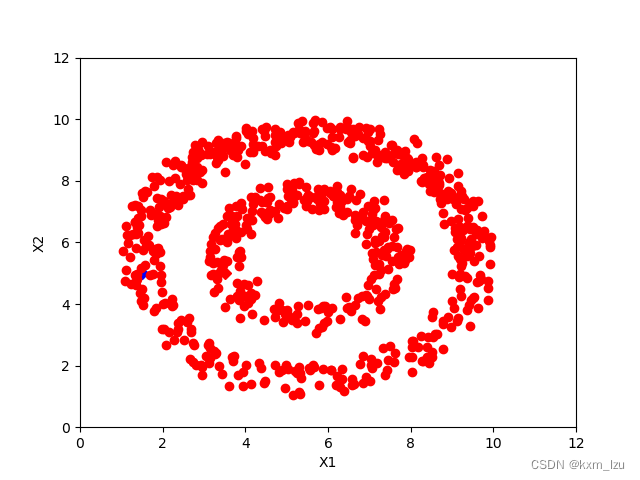
在这里插入图片描述

iter=10:
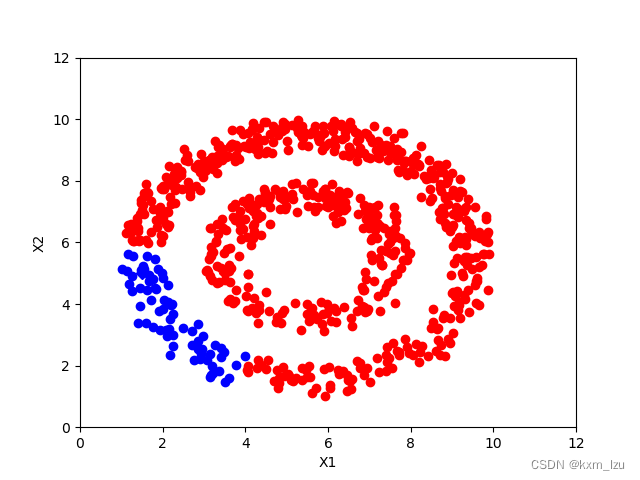
在这里插入图片描述
iter=30:

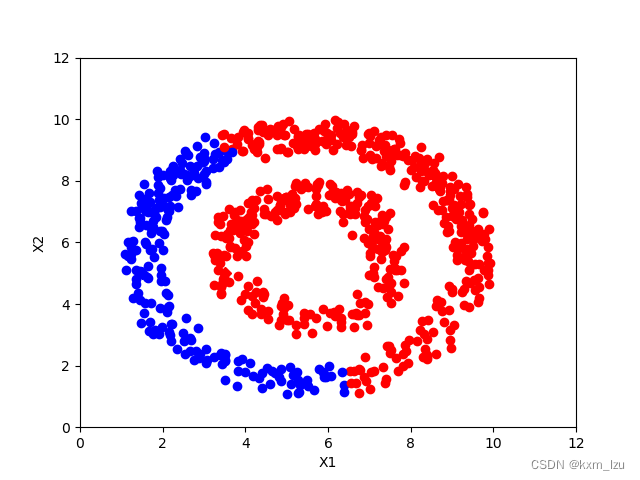
iter=100:

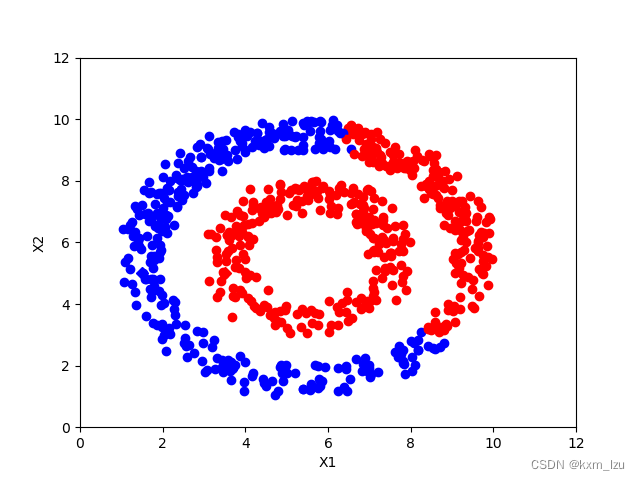
iter=150:

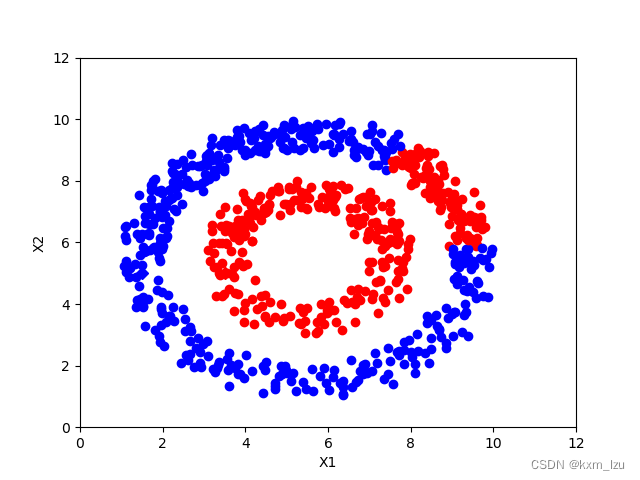
iter=300:

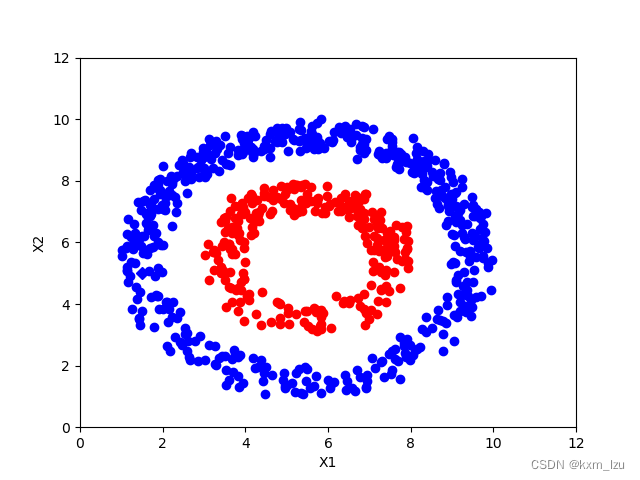
从图中可以清楚的看到传播的过程。
以上是自己在参考相关博客后得出的自己的一些理解，如有错误，还请不吝赐教,谢谢!
参考博客链接：
大佬的博客

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/339114