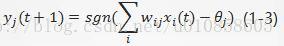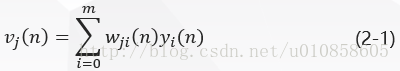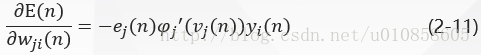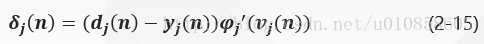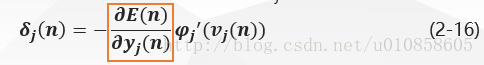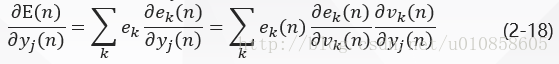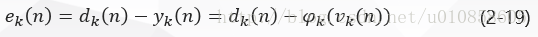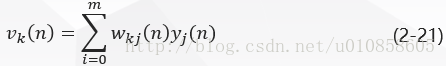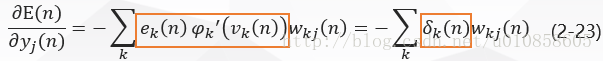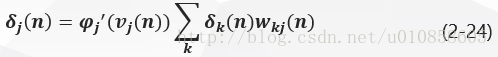BP 神经网络算法原理_bp神经网络原理csdn

一、 人工神经网络

1.人工神经网络简介

人工神经网络（ANN）是一种旨在模仿人脑结构及其功能的由多个非常简单的处理单元彼此按某种方式相互连接而形成的计算机系统，该系统靠其状态对外部输入信息的动态响应来处理信息 。

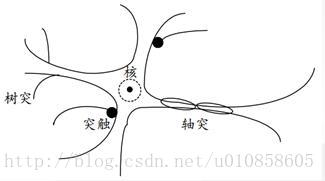
神经元由细胞及其发出的许多突起构成。细胞体内有细胞核，突触的作用是传递信息。作为引入输入信号的若干个突起称为“树突”，而作为输出端的突起只有一个称为“轴突” 。

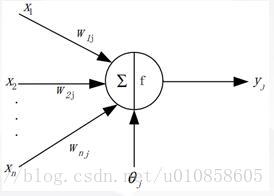
2.神经元M-P模型

所谓M-P模型,其实是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型。

对于第个神经元作用的加权值。

神经元的“净输入”用取+1 输出，反之为-1输出 。如果考虑输出与输入的延时作用，表达式可修正为：

3.ANN的基本要素

• 神经元激活函数
• 网络的学习
• 神经元之间的连接形式

（1）常用激活函数

（2）常用学习规则

• Hebb规则
• 误差修正法学习算法 （如：BP算法）
• 胜者为王(Winner-Take-All)学习规则

（3）神经元之间连接方式
<1>前缀网络

<2>反馈网络

> 注：BP 神经网络属于前缀网络

二、 BP 神经网络原理

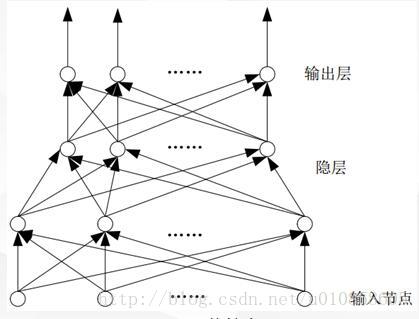
BP(Back Propagation)神经网络的学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经隐层逐层处理后，传向输出层。若输出层的实际输出与期望输出不符，则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。BP网络由输入层﹑输出层和隐层组成，为输出层，其余为隐层。BP 神经网络的结构如下：

这里介绍三层神经网络的推导（一个输入层、一个隐层和一个输出层）

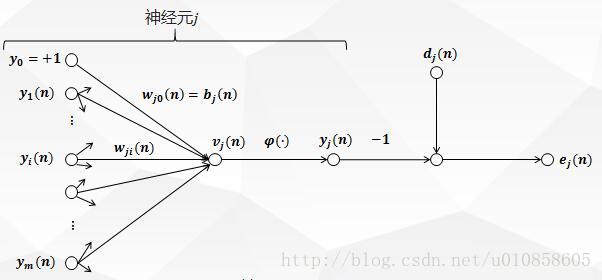
BP 神经网络反向传播算法的神经元示意图图一：

上图描绘了神经元。

1.前向传播过程推导

图一中，在神经元 的输入）是：

是：

2.误差反向传播过程推导

在图一中，的输出所产生的误差信号定义为：

其中，个元素。

为了使函数连续可导，这里最小化均方根差，定义神经元的瞬时误差能量为：

将所有输出层神经元的误差能量相加，得到整个网络的全部瞬时误差能量：

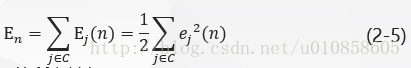
其中，集合C 包括输出层的所有神经元。

BP 算法通过反复修正权值使式(2-5)在权值空间的搜索方向。

在式(2-5)两边对取微分，得到：

在式(2-3)两边对取微分，得到：

在式(2-2)两边对取微分，得到：

最后在式(2-1)两边对取微分，得到：

将式(2-7)——(2-10)带入式(2-6)得：

应用于定义为：

其中，是误差反向传播的学习率， 负号表示在权空间中梯度下降。

将式(2-11)带入式(2-12)得：

其中，是根据delta法则定义的局部梯度：

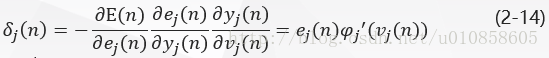
局部梯度指明了突触权值所需要的变化。

现在来考虑神经元所处的层。

（1） 神经元是输出层节点

当神经元为：

（2） 神经元是隐层节点

当神经元根据式(2-14)重新定义为：

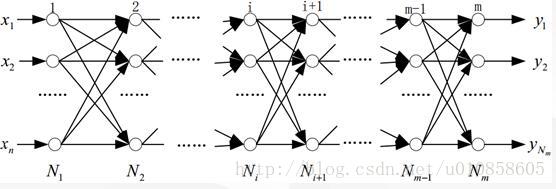
来看图二：它表示输出层神经元表示输出层神经元。

图二中，网络的全部瞬时误差能量为：

在式(2-17)两边对函数信号求偏导，得到：

在图二中：

因此，

图二中，对于输出层神经元 ，其诱导局部域是：

求式(2-21)对的微分得到：

将式(2-20)和(2-22)带入到式(2-18)得到：

将式(2-23)带入式(2-16)得隐层神经元为：

反向传播过程推导总结

因此，结合式(2-13)、(2-15)和(2-24)，由神经元按照delta法则定义如下：

其中：

• 神经元与权值加权和的乘积，见式(2-24)。

3.标准BP神经网络设计原则

（1）激活函数
单极性S型函数和双曲正切S型函数
（2）学习率
或

隐层节点数=

4.标准BP算法训练过程及流程图

（1）训练过程

1. 初始化网络的突触权值和阈值矩阵；

2. 训练样本的呈现；

3. 前向传播计算；

4. 误差反向传播计算并更新权值；

5. 迭代，用新的样本进行步骤3和4，直至满足停止准则。

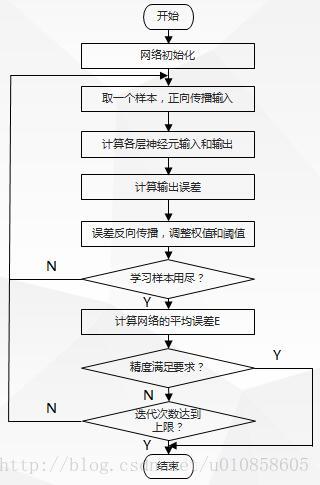
（2）流程图

5.标准BP算法分析

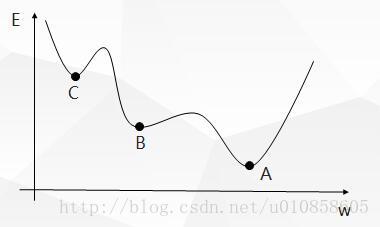
由于标准 BP 算法采用的是梯度下降法，BP 算法的 E-w 曲线图如下：

因此标准 BP 算法具有以下缺陷：

1. 在误差曲面上有些区域平坦，此时误差对权值的变化不敏感，误差下降缓慢，调整时间长，影响收敛速度。
2. 存在多个极小点，梯度下降法容易陷入极小点而无法得到全局最优解。
3. 学习率越大，虽然学习速度加快，却容易使权值的变化量不稳定，出现振荡。

6.标准BP算法改进方法

（1）增加动量项
一个既要加快学习速度又要保持稳定的方法是修改式(2-13)，增加动量项，表示为：

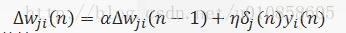
这里<1。

动量项≠0，使其跳出局部极小区域，加快迭代收敛速度。

（2）其他改进方法

• 可变学习速度的反向传播
• 学习速率的自适应调节
• 引入陡度因子——防止饱和
• 共轭梯度法、拟牛顿法等