自然语言处理评价指标

训练好的模型，上线之前要对模型进行必要的评估，目的让模型对语料具备较好的泛化能力。具体有以下这些指标可以参考。

1.错误率、精度、准确率、精确度、召回率、F1 衡量。

错误率：是分类错误的样本数占样本总数的比例。对样例集 D，分类错误率计算公式如下

精度：是分类正确的样本数占样本总数的比例。这里的分类正确的样本数指的不仅是正例分类正确的个数还有反例分类正确的个数。对样例集 D，精度计算公式如下：

 

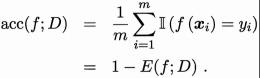
混淆矩阵

True Positive(真正，TP)：将正类预测为正类数

True Negative(真负，TN)：将负类预测为负类数

False Positive(假正，FP)：将负类预测为正类数误报 (Type I error)

False Negative(假负，FN)：将正类预测为负类数→漏报 (Type II error)

对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为真正例（True Positive）、假正例（False Positive）、真反例（True Negative)、假反例（False Negative）四种情形，令 TP、FP、TN、FN 分别表示其对应的样例数，则显然有 TP+FP++TN+FN=样例总数。分类结果的“混淆矩阵”（Confusion Matrix）如下：

准确率，缩写表示用 P。准确率是针对我们预测结果而言的，它表示的是预测为正的样例中有多少是真正的正样例。定义公式如下

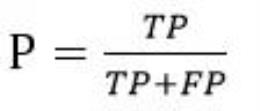
精确度，准确率，缩写表示用 A。精确度则是分类正确的样本数占样本总数的比例。Accuracy 反应了分类器对整个样本的判定能力（即能将正的判定为正的，负的判定为负的）。定义公式如下：

      准确率是我们最常见的评价指标，而且很容易理解，就是被分对的样本数除以所有的样本数，通常来说，正确率越高，分类器越好。 准确率确实是一个很好很直观的评价指标，但是有时候准确率高并不能代表一个算法就好。

      比如某个地区某天地震的预测，假设我们有一堆的特征作为地震分类的属性，类别只有两个：0：不发生地震、1：发生地震。一个不加思考的分类器，对每一个测试用例都将类别划分为0，那那么它就可能达到99%的准确率，但真的地震来临时，这个分类器毫无察觉，这个分类带来的损失是巨大的。为什么99%的准确率的分类器却不是我们想要的，因为这里数据分布不均衡，类别1的数据太少，完全错分类别1依然可以达到很高的准确率却忽视了我们关注的东西。

     再举个例子说明下。在正负样本不平衡的情况下，准确率这个评价指标有很大的缺陷。比如在互联网广告里面，点击的数量是很少的，一般只有千分之几，如果用acc，即使全部预测成负类（不点击）acc也有 99% 以上，没有意义。因此，单纯靠准确率来评价一个算法模型是远远不够科学全面的。

召回率，缩写表示用 R。召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确。定义公式如下：

注： 那也有两种可能，一种是把原来的正类预测成正类(TP)，另一种就是把原来的正类预测为负类(FN)
召回率是覆盖面的度量，度量有多个正例被分为正例

F1 衡量，表达出对查准率/查全率的不同偏好。定义公式如下：

2.ROC 曲线、AUC 曲线。

ROC 全称是“受试者工作特征”（Receiver Operating Characteristic）曲线。我们根据模型的预测结果，把阈值从0变到最大，即刚开始是把每个样本作为正例进行预测，随着阈值的增大，学习器预测正样例数越来越少，直到最后没有一个样本是正样例。在这一过程中，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了 ROC 曲线。

其中： 
（1）曲线与FP_rate轴围成的面积（记作AUC）越大，说明性能越好，即图上L2曲线对应的性能优于曲线L1对应的性能。即：曲线越靠近A点（左上方）性能越好，曲线越靠近B点（右下方）曲线性能越差。 
（2）A点是最完美的performance点，B处是性能最差点。 
（3）位于C-D线上的点说明算法性能和random猜测是一样的–如C、D、E点。位于C-D之上（即曲线位于白色的三角形内）说明算法性能优于随机猜测–如G点，位于C-D之下（即曲线位于灰色的三角形内）说明算法性能差于随机猜测–如F点。 
（4）虽然ROC曲线相比较于Precision和Recall等衡量指标更加合理，但是其在高不平衡数据条件下的的表现仍然过于理想，不能够很好的展示实际情况。

ROC 曲线的纵轴是“真正例率”（True Positive Rate, 简称 TPR)，横轴是“假正例率”（False Positive Rate,简称FPR），两者分别定义为：

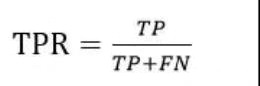
ROC 曲线的意义有以下几点：

1. ROC 曲线能很容易的查出任意阈值对模型的泛化性能影响；
2. 有助于选择最佳的阈值；
3. 可以对不同的模型比较性能，在同一坐标中，靠近左上角的 ROC 曲所代表的学习器准确性最高。

如果两条 ROC 曲线没有相交，我们可以根据哪条曲线最靠近左上角哪条曲线代表的学习器性能就最好。但是实际任务中，情况很复杂，若两个模型的 ROC 曲线发生交叉，则难以一般性的断言两者孰优孰劣。此时如果一定要进行比较，则比较合理的判断依据是比较 ROC 曲线下的面积，即AUC（Area Under ROC Curve）。

AUC 就是 ROC 曲线下的面积，衡量学习器优劣的一种性能指标。AUC 是衡量二分类模型优劣的一种评价指标，表示预测的正例排在负例前面的概率。

AUC值越大的分类器，正确率越高

完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
跟随机猜测一样（例：丢铜板），模型没有预测价值。
比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在 的情况

前面我们所讲的都是针对二分类问题，那么如果实际需要在多分类问题中用 ROC 曲线的话，一般性的转化为多个“一对多”的问题。即把其中一个当作正例，其余当作负例来看待，画出多个 ROC 曲线。