惯性导航原理（1）：导航坐标系及相互转换_惯导坐标转换

写在前面（本人是导航专业，目前已经毕业入职，工作也是与惯导、组合导航相关，因为以前的知识忘的差不多了，所以开个帖子，会分几章记录一下，如有不正确的地方还请大家多多指教）
补充 由于不同参考资料中，经纬度表示不同，有的是L表示纬度， $\lambda$表示经度，有的是B表示纬度，L表示经度，由于本文参考了很多资料，且博主较懒，不想打公式因此文中经纬度、卯酉圈子午圈符号有些混乱，但是已在文中加了注释

坐标系介绍

1、惯性坐标系（地心惯性坐标系）i系

  O-XiYiZi，角标常用i表示。取地球中心为坐标原点O，OZ轴沿地球自转轴方向，OX轴是地球绕太阳公转的黄道平面与地球赤道平面的交线，OY轴沿右手规则确定。需要注意：地心坐标系是不与地球固联的，它不随地球自转而转动。（IMU（加表、陀螺）测量的就是相对于惯性系的运动）

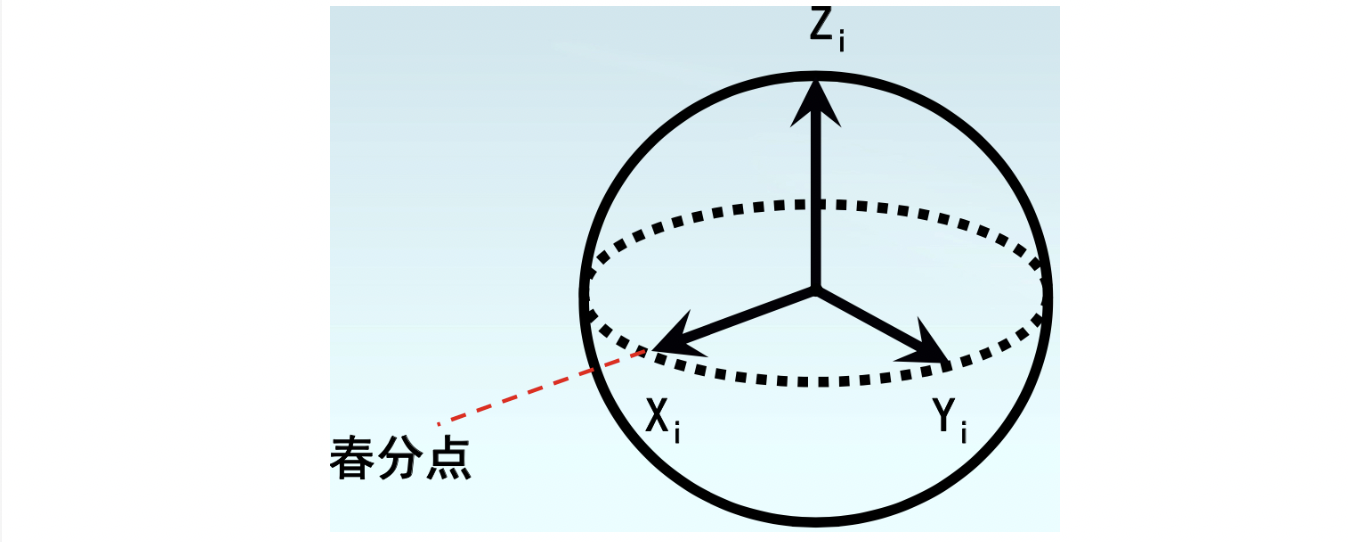
2、地球坐标系（地心地固坐标系）e系

  其原点为地球的质心，X轴延伸通过本初子午线（0度经度）和赤道的交点；Z轴延伸通过的北极（即与地球旋转轴重合）；Y轴与X、Z轴形成右手坐标系，穿过赤道和90度经度。常表示为O-XeYeZe。导航中，一般关心的是载体相对于地球的位置，故e系常作为参考坐标系。

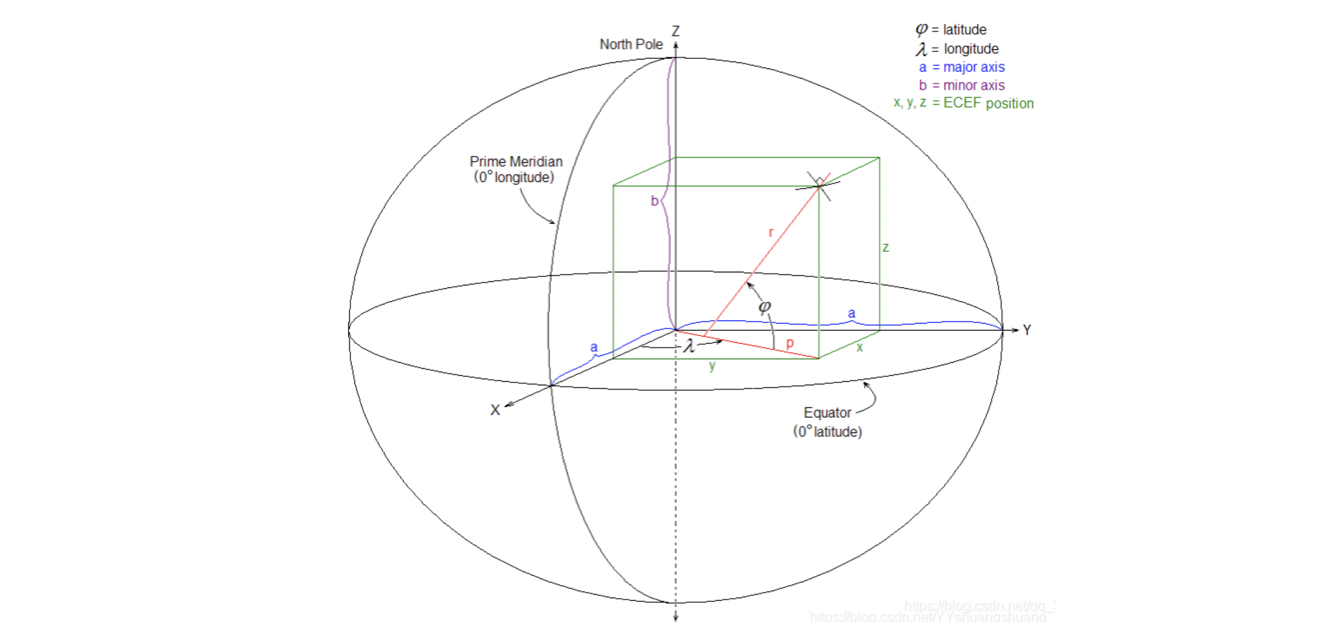
3、WGS-84坐标系（常用）blh坐标系

  wgs84表示的就是地理经纬度，也叫经纬高坐标系(经度(longitude)，纬度(latitude)和高度(altitude)LLA坐标系)。我们常说的经纬度一般都是wgs84。只不过由于地球是不规则的，所以地理坐标系分为很多种，GPS是美国的，采用的就是WGS84坐标系，中国一般使用北京54、西安80、China2000等。WGS-84坐标系的X轴指向BIH(国际时间服务机构)1984.0定义的零子午面(Greenwich)和协议地球极(CTP)赤道的交点。Z轴指向CTP方向。Y轴与X、Z轴构成右手坐标系。

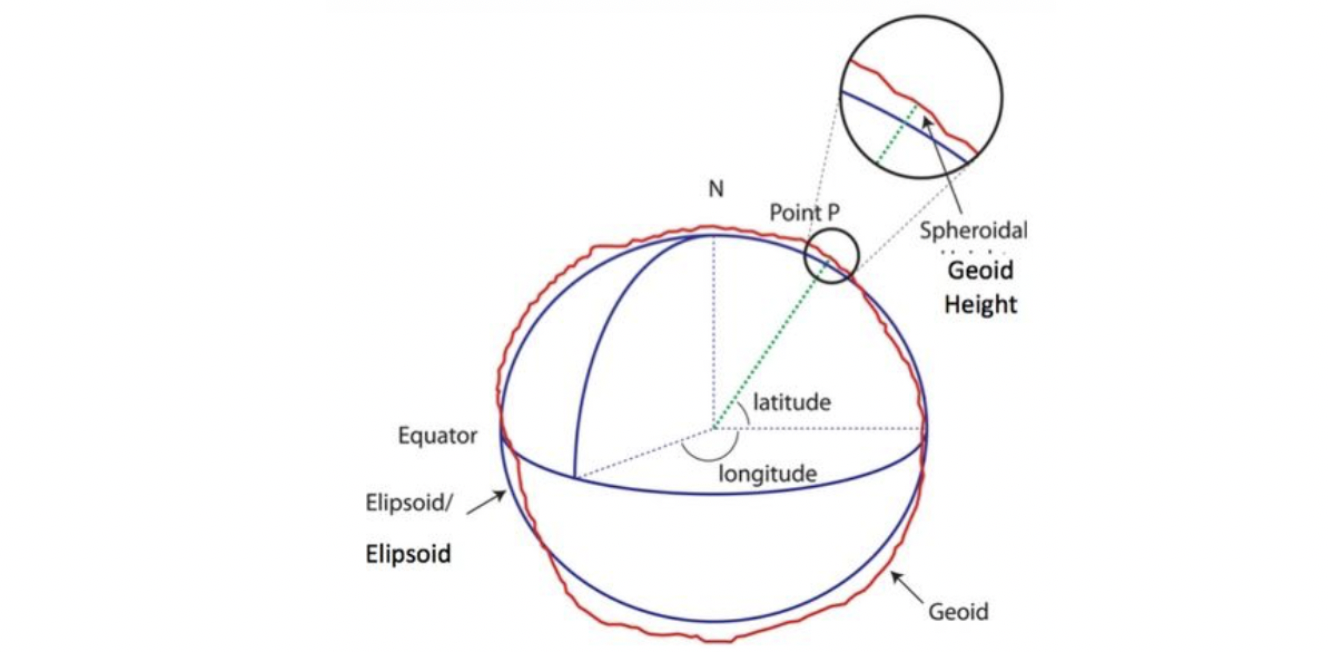
  1、大地纬度是过用户点P的基准椭球面法线与赤道面的夹角。纬度值在-90°到+90°之间。北半球为正，南半球为负。
  2、大地经度是过用户点P的子午面与本初子午线之间的夹角。经度值在-180°到+180°之间。
  3、大地高度h是过用户点P到基准椭球面的法线距离，基准椭球面以内为负，以外为正。

4、当地水平地理坐标系g系（常用东北天ENU或者北东地NED）

  以东北天坐标系为例：
  以点P为原点，以 P点的法线为Z轴，指向天顶为正，以子午线方向为Y轴，指向北为正，X 轴与YZ 平面垂直，向东为正
  北东地坐标系定义为：X轴：指向正北；Y轴：指向东向；Z轴：与XY轴形成右手坐标系，指向地向。

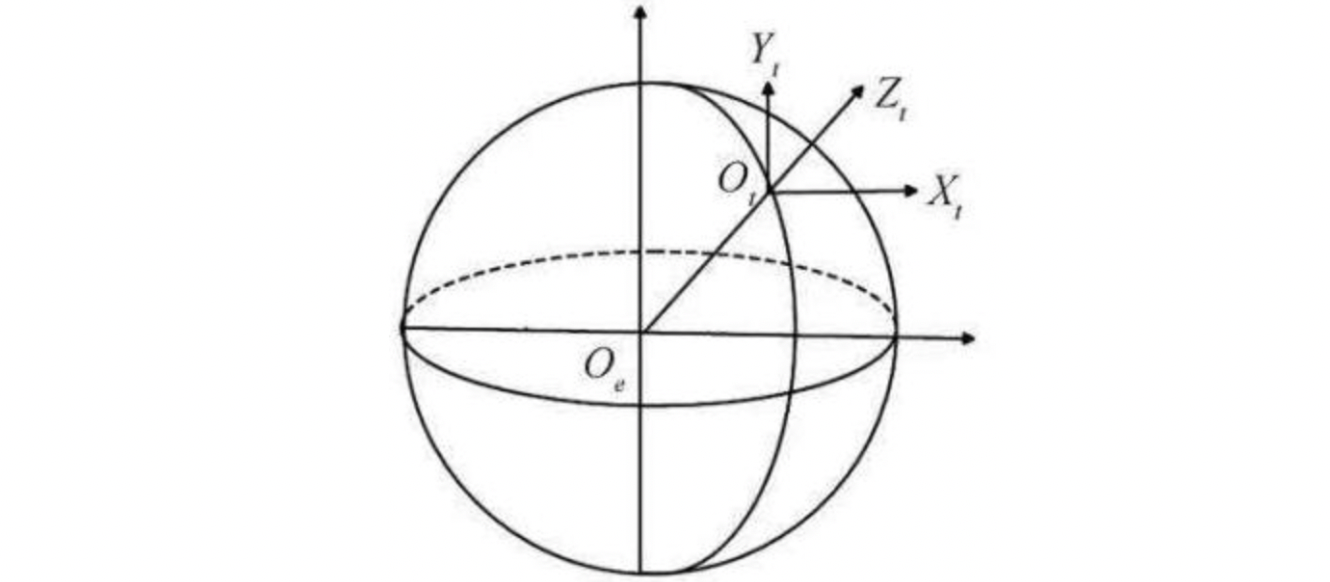
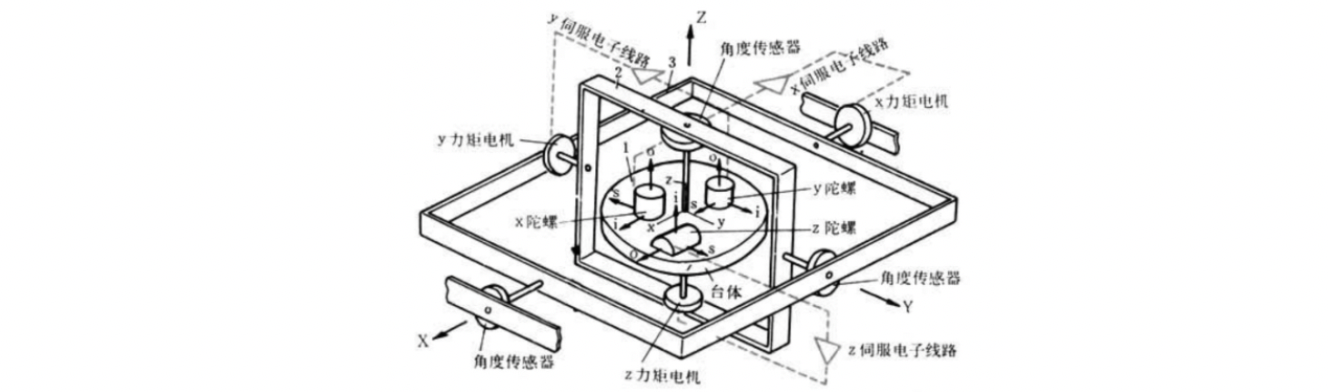
5、平台坐标系p系

  描述平台式惯导系统中平台指向的坐标系叫做平台坐标系，它与平台固连。如果平台无误差，指向正确，则这样的平台坐标系称为理想平台坐标系。（目前我使用的基本是捷联惯导，所以这个坐标系下文几乎不会涉及，仅仅这里介绍一下）

6、导航坐标系n系

  导航坐标系是惯性导航算法的基本参考系，运动物体在导航坐标系内进行位置、速度、姿态确定，可选取e系或g系做为导航系。在e系内导航，可以直接确定地心地固系下的导航参数，便于和GNSS 等大地测量手段相结合，在惯性导航中，经常将地理坐标系g作为导航坐标系。值得注意的是，导航坐标系只是一个“虚”的概念。

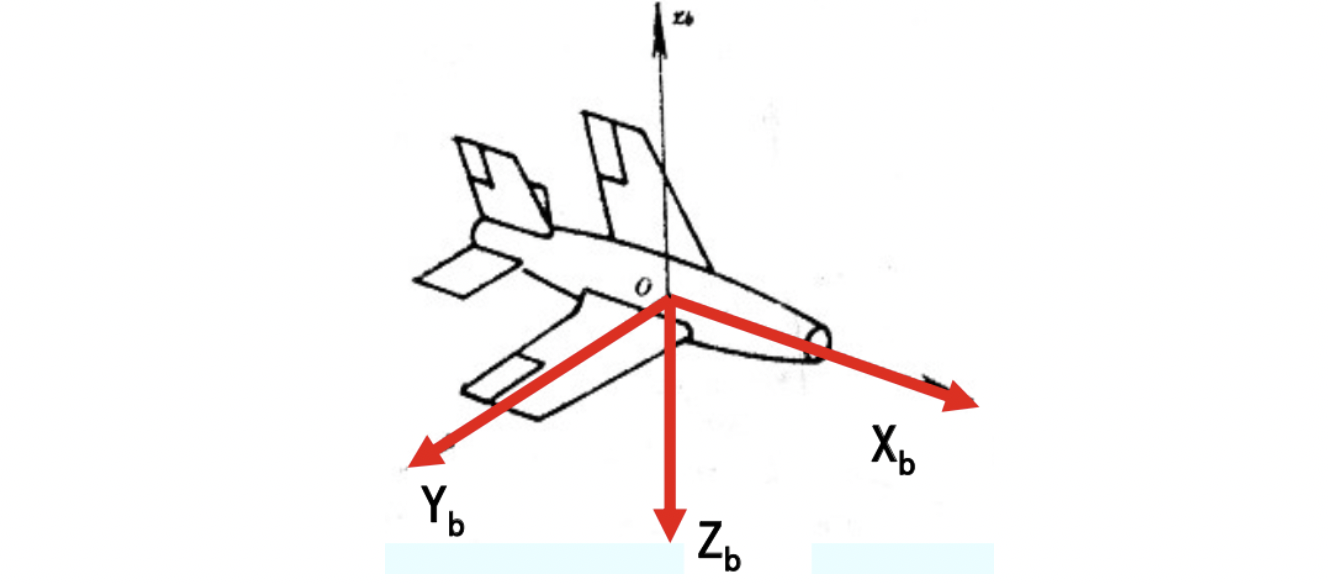
7、载体坐标系b系

  该系固定在载体上，时刻随着载体运动而运动。其原点与载体质心重合。
  与东-北-天对应的载体系是右-前-上坐标系，X轴沿运载体横轴线指右，Y轴沿纵轴指前，Z轴沿运载体竖向并与X、Y轴构成右手直角坐标系。
  与北-东-地对应的载体系是前-右-下坐标系，X轴沿载体纵轴指前，Y轴指右，Z轴沿载体竖轴与X、Y轴构成右手直角坐标系。

坐标系间的相对转换关系

1、惯性坐标系i系<=>地心地固坐标系e系

  惯性坐标系i与地心地固坐标系e系之间原点重合，二者之间存在相对旋转，角速度指向Z轴，自西向东旋转，地球自转角速度（e系相对于i系）为7.292115e-5 rad/s，i系到e系的坐标转换矩阵为：

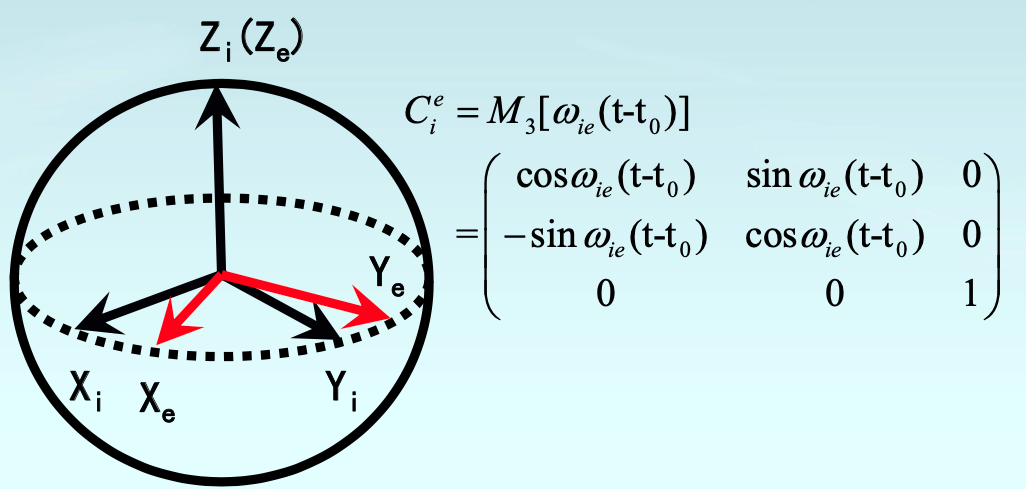
  而e系到i系的坐标旋转矩阵只需要将i系到e系的坐标转换矩阵转置即可。

2、blh坐标系<=>地心地固坐标系e系

  求解blh坐标系与地心地固坐标系间的坐标旋转矩阵之前，需要了解何为子午圈半径与卯酉圈半径：

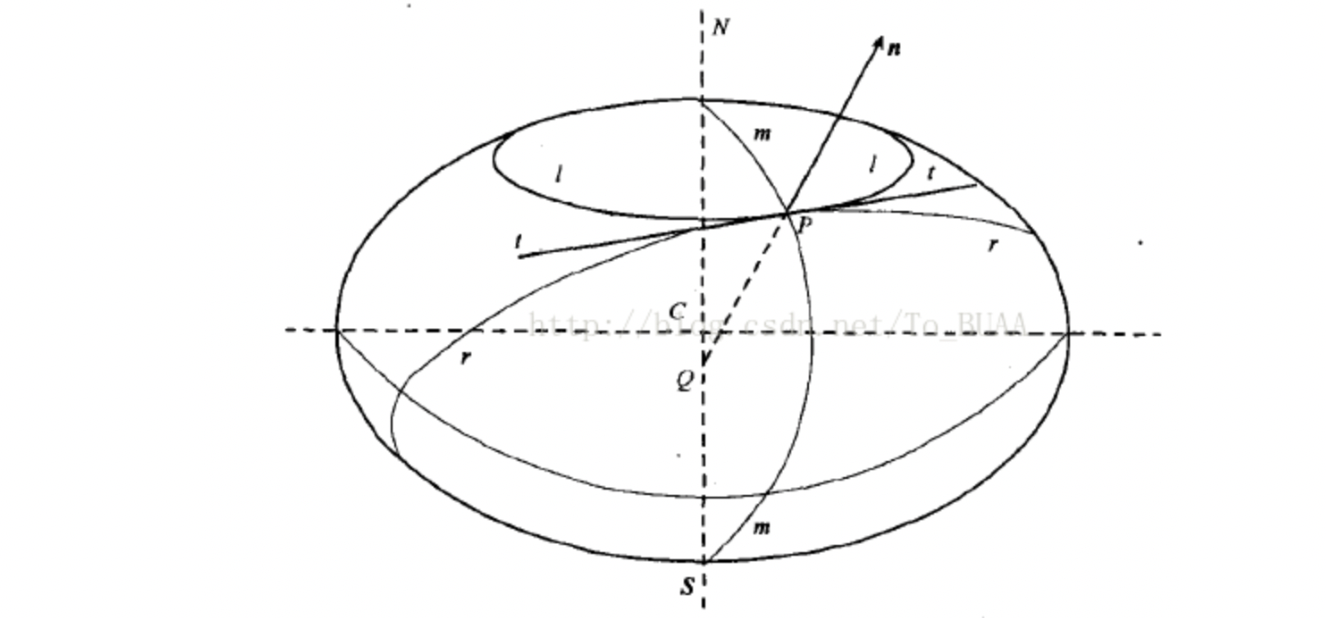
  设P点为旋转椭球体上某一点，n为P点处的法线，NS为椭球面的对称轴，过P作NS的垂直平面，截椭球面所得的平面曲线lPl称为P点处的纬圈，过P点和直线NS作平面截椭球面所得的平面曲线mPm称为 经圈（子午圈），过P点作纬圈lPl的切线tPt，用tPt和法线n形成的平面截椭球面所得的平面曲线rPr称为P点处的卯酉圈。P点处沿子午圈mPm的曲率半径Rm（有称Rn）为子午圈曲率半径，沿卯酉圈的曲率半径rPr的曲率半径Rn（有称Re）卯酉圈曲率半径。计算公式如下：

  其中，R为地球赤道半径（椭圆的长半轴），WGS-84模型中，R = 6378137m，e为第一偏心率，e = 0.0818191908426，f为第一扁率，f = 1/298.257223563。
  在高度为h处的子午圈半径为Rn+h，卯酉圈半径为Re+h。
  则：blh坐标系->地心地固坐标系e系的坐标转换矩阵为：

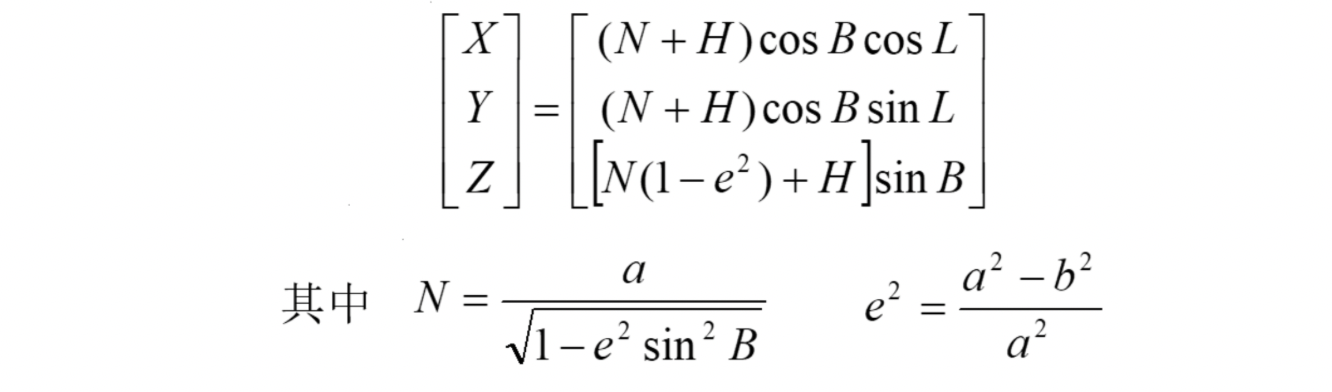
  上式中：N为卯酉圈曲率半径（同上面的Re）；a为地球椭球的长半轴；b为地球椭球的短半轴，B为P点的纬度，L为P点的经度。
  地心地固坐标系e系->blh坐标系的坐标转换矩阵为：

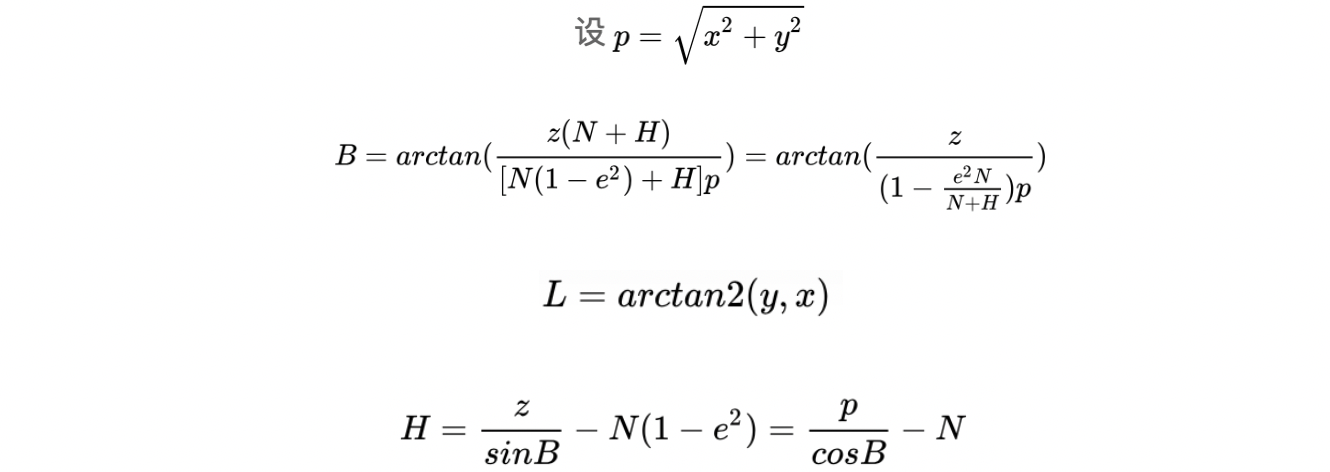
3、地心地固坐标系e系<=>当地水平地理坐标系g系

  地理坐标系g与地球坐标系e之间的转动关系可以用方向余弦阵表示，常称之为位置矩阵：

1、g系选取为东北天坐标系

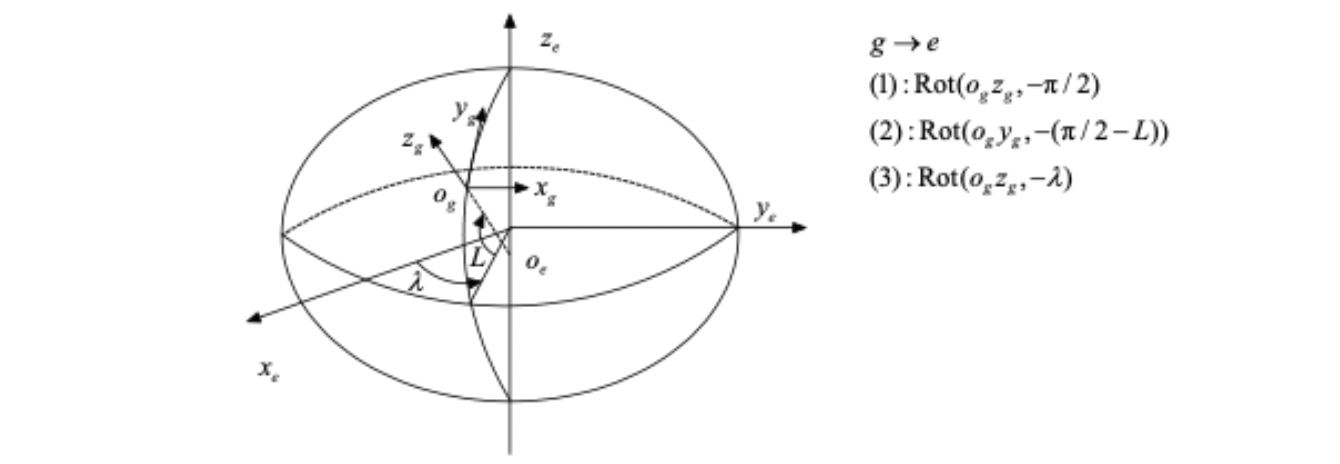
  g系先绕OZ轴转动-pi/2，接着绕OY轴转动-(pi/2-B)，其中B为纬度（弧度表示），再绕OZ轴转动-L，其中L为经度（弧度表示），此时g系与e系坐标轴平行。

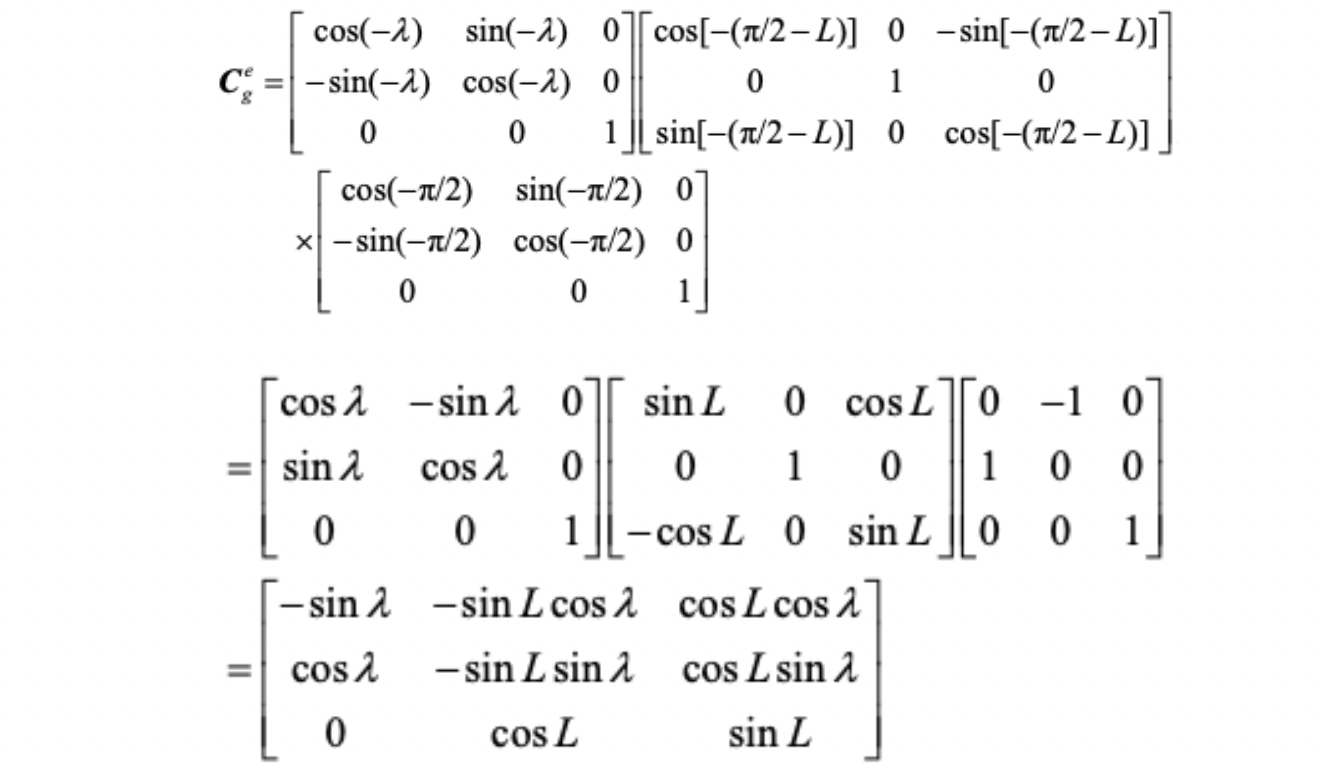
  e系到g系的坐标转换矩阵只需要将上式转置即可。

2、g系选取为北东地坐标系

  e系转到g系（北东地）的坐标旋转矩阵$C_g^e$ 表示如下：（由于常将地理坐标系g作为导航坐标系，因此表示成$C_n^e$是同一个东西 ）：

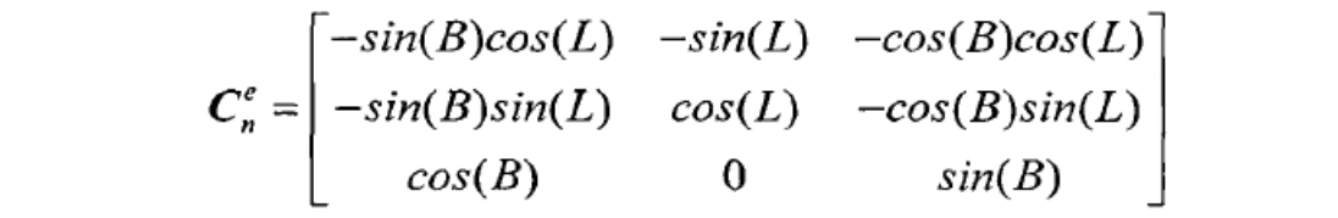
  e系到g（n）系的坐标转换矩阵只需要将上式转置即可。

4、当地水平地理坐标系g（n）系<=>载体坐标系b系

1、g（n）系选取为东北天坐标系，b系选择右前上坐标系

  欧拉角表达式为：

  东北天——右前上坐标系下欧拉角旋转顺序：航向角（绕Z轴）—俯仰角（绕X轴）—横滚角（绕Y轴）：
  第一个转动角度：航向角（绕Z轴旋转$-\psi$角）
  第二个转动角度：俯仰角（绕X轴旋转 $\theta$ 角）
  第三个转动角度：横滚角（绕Y轴旋转$\varphi$角）
  注意 俯仰角和横滚角：姿态角方向与对应轴向转动方向一致，绕对应轴正转，相应姿态为正，绕对应轴反转，相应姿态为负。航向角：姿态角方向与对应轴向转动方向相反（由于航向角定义为：Y轴指北时，航向角为零。北偏东顺时针依次从0变为360deg。而Z轴指天，Z轴反转时，航向角才依次增大）。
  则旋转矩阵为:

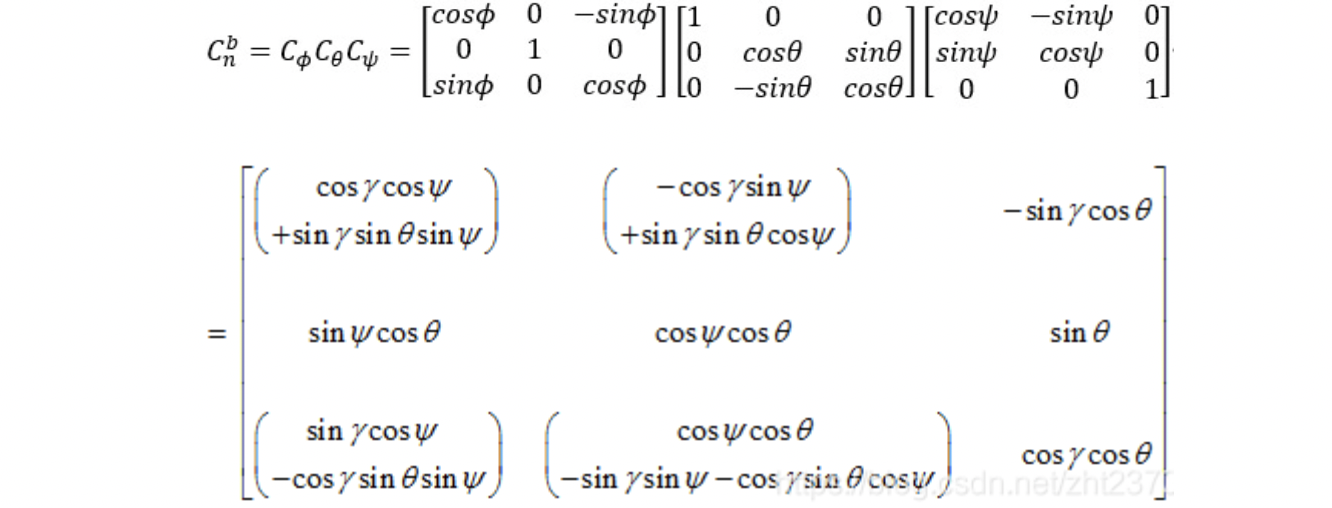
  所以姿态矩阵（b系到n系的坐标转换矩阵）为：

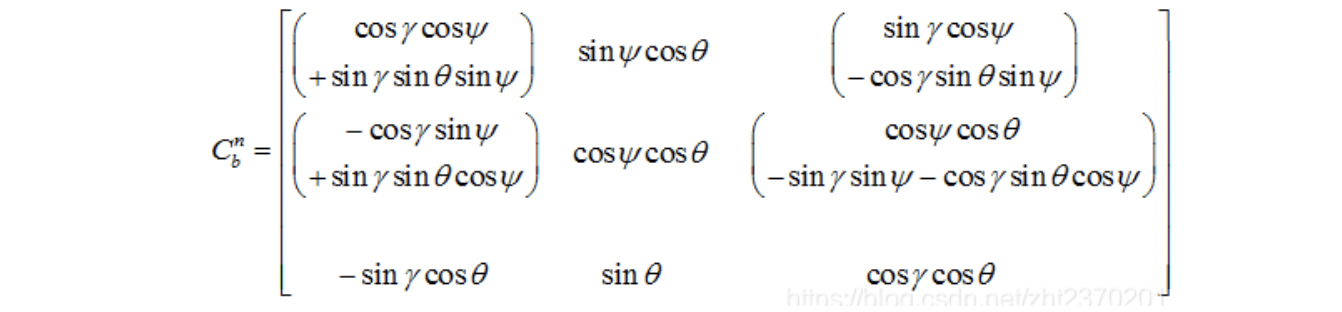
2、g（n）系选取为北东地坐标系，b系选择前右下坐标系

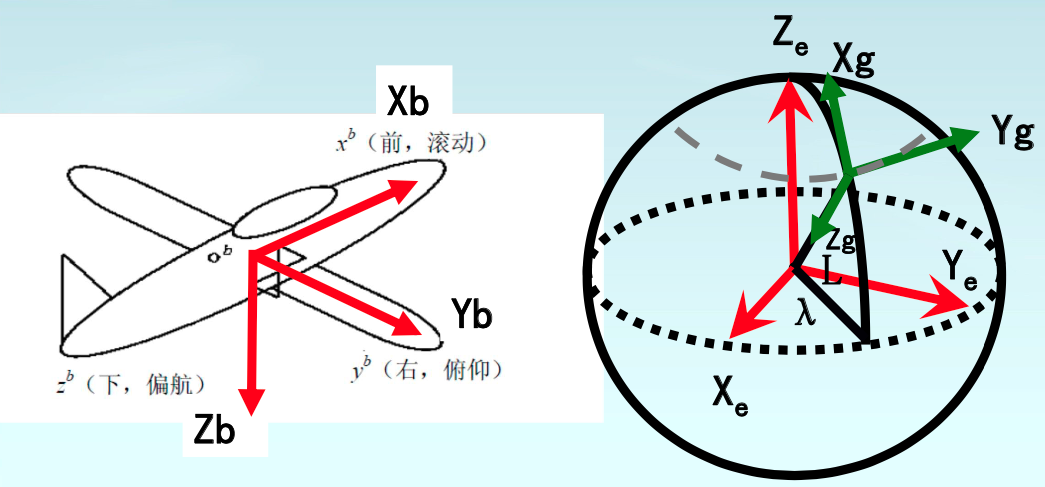
  北东地——前右下坐标系下欧拉角旋转顺序：航向角（绕Z轴）—俯仰角（绕Y轴）—横滚角（绕X轴）：
  第一个转动角度：航向角（绕Z轴旋转$\psi$角）
  第二个转动角度：俯仰角（绕Y轴旋转 $\theta$ 角）
  第三个转动角度：横滚角（绕X轴旋转$\varphi$角）
  注意 俯仰角和横滚角：方向与对应轴向转动方向一致，绕对应轴正转，相应姿态为正；绕对应轴反转，相应姿态为负。X轴指北时，航向角为零。北偏东顺时针依次从0变为360deg
  （个人感觉北东地坐标系要比东北天坐标系好用一些，然而国内的大佬秦永元、严恭敏等均用的东北天坐标系，北东地坐标系国外学者用的多一些）。
则旋转矩阵为：

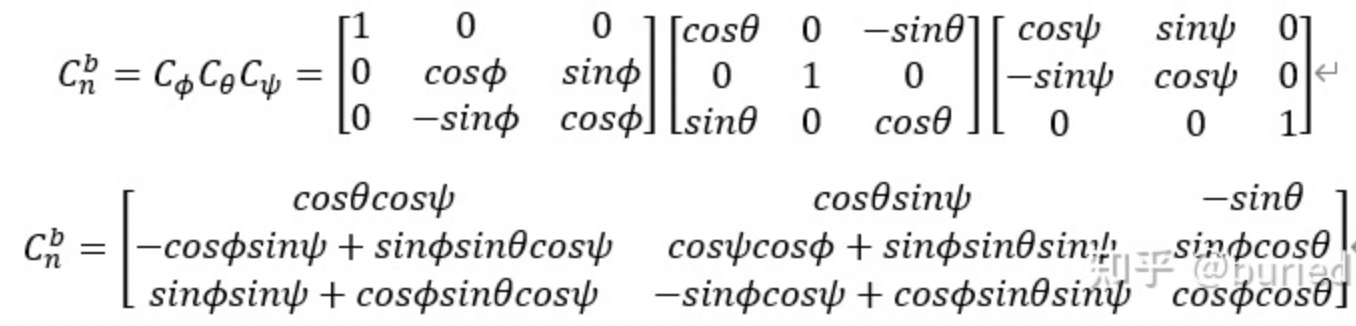
  则旋转矩阵为:

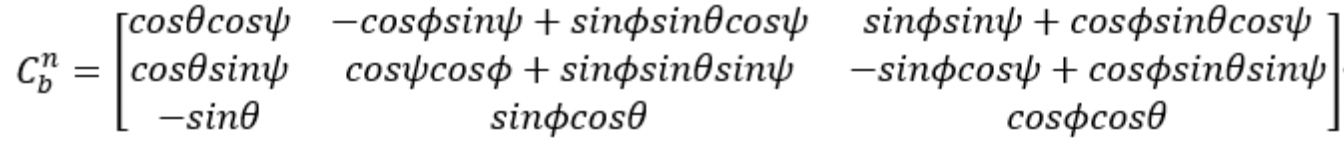
  最后一定注意欧拉角旋转顺序与定义啊兄弟们，别搞混了，坐标系选取不同定义也不同的！！！！！！