深度剖析图像处理—边缘检测
赞
踩
什么是边缘检测
边缘检测(Edge Detection)就是提取图像中的边缘点(Edge Point)。边缘点是与周围像素相比灰度值有阶跃变化或屋顶状变化的像素。边缘常存在于目标与背景之间、目标与目标之间、目标与其影子之间。
在图像处理和图像分析中,经常要用到边缘(Edge)、边界(Boundary)、轮廓(Contour)等术语。一般来说,边缘指的是边缘点,它不能被称为边缘线。边界指的是图像中不同区域之间的分界线,比如不同灰度、不同颜色的区域之间的分界线,它是线而不是点,可以被称为边界线。轮廓一般是指目标的轮廓,目标就是语义明确的区域,轮廓一般是在二值图像中围绕白色区域的闭合曲线。
边缘检测算法和边界线检测算法一般作用于灰度图像,对于二值图像进行边缘检测是没有意义的。轮廓一定是闭合的,但边界线不一定闭合,比如道路区域与道边植被的边界线;边缘点最多是断断续续的线段,不保证连续,更不保证闭合。掌握边缘、边界、轮廓的准确术语是非常必要的。
边缘类型
边缘检测是一种邻域运算,即一个像素是否是边缘点是由其所处的邻域决定的。在一定大小的邻域内,边缘分为阶跃边缘(step edge)和屋顶状边缘(roof edge)两种类型。下面以一维信号为例,分析这两种不同类型的边缘的导数特征
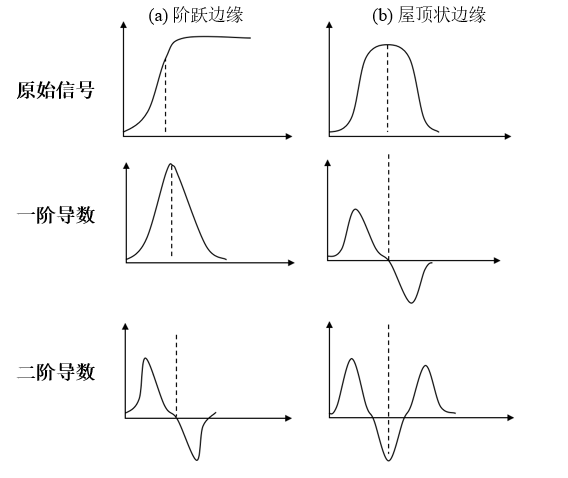
求导与差分
在边缘检测中,导数的计算通常采用两种方法:
-
将邻域从离散空间变换到连续空间,得到解析描述,然后进行求导操作**。**
具体做法是,先将**邻域按照一定的数学模型(曲线拟合、曲面拟合)得到其在连续空间中的解析描述,然后对此解析描述进行求导,得到边缘点。解析描述求导得到的导数位置是有小数位的,比如在位置4.17处取得导数最大值,即边缘点的位置是在4.17而不是像素的整数坐标4。这样得到的边缘点位置精度能够小于1个像素,因此又将此方法称之为亚像素(sub pixel)边缘检测。在已知数学模型的指导下,目前工业界做到的边缘检测最高精度为1/50个像素。**亚像素边缘检测能够在大大节省硬件成本的同时,得到高的边缘检测精度,是图像测量中的常用方法。
-
直接用差分(difference)代替求导。导数的公式见下式,如果令dx=1,即得到是差分描述,式(4-2)是差分描述的x方向偏导数,式(4-3)是差分描述的y方向偏导数。
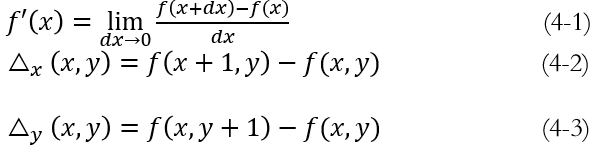
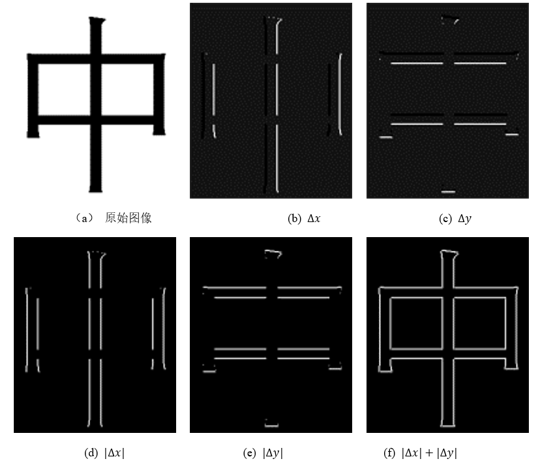
边缘强度与边缘方向
导数是有大小也有方向的,因此边缘也有强弱与方向,分别叫做边缘强度(edge intensity)和边缘方向(edge direction),边缘强度即边缘的幅值(magnitude)。用M(x,y)代表边缘的强度,θ(x,y)代表边缘的方向,有:
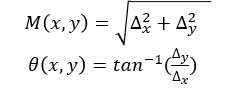
实例
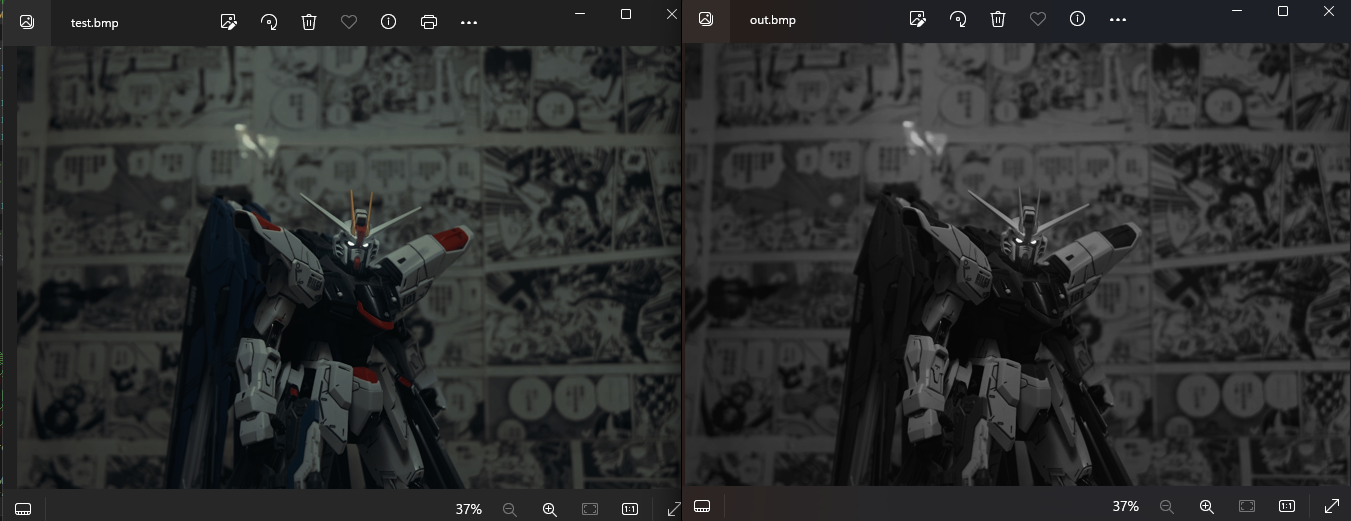
我们该如何提取这张图片的边缘呢?

首先当然是需要我们写一个函数来把24位彩色图像转化为8位灰度值图像
//24位彩色图像转8位灰度值 //rgbImage原始图像 //grayImage输出灰度图像 //width,height图片的宽和高 void convertToGray(uint8_t* rgbImage, uint8_t* grayImage, int width, int height) { for (int y = 0; y < height; y++) { for (int x = 0; x < width; x++) { // 获取当前像素的 RGB 分量 uint8_t r = rgbImage[3 * (y * width + x) + 0]; uint8_t g = rgbImage[3 * (y * width + x) + 1]; uint8_t b = rgbImage[3 * (y * width + x) + 2]; // 计算灰度值(常用的加权平均法) // 这里使用的加权系数是常见的:R: 0.299, G: 0.587, B: 0.114 uint8_t gray = (uint8_t)(0.299 * r + 0.587 * g + 0.114 * b); // 将灰度值写入灰度图像数组 grayImage[y * width + x] = gray; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
我们来看看效果
那接下来就需要用边缘检测来提取边缘了
一阶微分算子
根据边缘类型及其导数特征,可以设计不同的检测算法。下面讲述几种常用的边缘检测算法,习惯上称为边缘检测算子(Operator)。当使用差分时,一般写成模板的表示形式。
对于阶跃边缘而言,边缘点处的导数特征是“一阶导数取极值”。若边缘点处的一阶导数为正值,则其为最大值;反之,则为最小值,即在边缘点处的导数绝对值最大。
基于一阶导数的边缘检测算子称为一阶微分算子,常用的一阶微分算子有梯度算子、罗伯特算子、索贝尔算子、Prewitt算子,Robinson算子、Kirsch算子等。
梯度算子
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。梯度的含义和边缘点是一致的,因此产生了边缘检测的梯度算子(Gradient Operator)
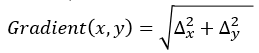
写成模板的情况就是如下图所示:

但是上面我们只是给出了像素(x,y)的边缘强度,称为梯度值;但是它是不是边缘点,还需要一定的约束条件,比如,设定当Gradient(x,y)≥threshold时,像素(x,y)才是边缘点,threshold称为阈值。

这就是用梯度算子计算的结果,我们上代码看看
void RmwGradientGryImg(uint8_t* pGryImg, int width, int height, uint8_t* pGrdImg) { uint8_t* pGry, * pGrd; int dx, dy; int x, y; for (y = 0, pGry = pGryImg, pGrd = pGrdImg; y < height - 1; y++) { for (x = 0; x < width - 1; x++, pGry++) { dx = *pGry - *(pGry + 1); dy = *pGry - *(pGry + width); int gradient = (int)(sqrt(dx * dx * 1.0 + dy * dy)); *pGrd++ = (gradient > 255) ? 255 : gradient; } *pGrd++ = 0; //尾列不做,边缘强度赋0 pGry++; } memset(pGrd, 0, width); //尾行不做,边缘强度赋0 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
这里简单说一下这个函数
- 函数参数:
pGryImg:输入的灰度图像数据指针。width:图像的宽度。height:图像的高度。pGrdImg:输出的梯度图像数据指针。- 双层循环:
- 外层循环
for (y = 0, pGry = pGryImg, pGrd = pGrdImg; y<height-1; y++)遍历图像的每一行,pGry和pGrd分别指向当前行的灰度图像数据和梯度图像数据。- 内层循环
for (x = 0; x<width-1; x++, pGry++)遍历当前行的每个像素,pGry指向当前像素的灰度值。- 计算梯度:
- 梯度的计算采用的是简单的基于像素差值的方法,分别计算水平方向和垂直方向的梯度。
dx = *pGry-*(pGry+1):水平方向的梯度,计算当前像素和右侧像素的灰度差值。dy = *pGry-*(pGry+width):垂直方向的梯度,计算当前像素和下方像素的灰度差值。sqrt(dx*dx*1.0+dy*dy):使用欧式距离公式计算梯度幅值。min(255, ...):确保梯度幅值不超过255,限定在0到255之间。- 内存清零:
memset(pGrd, 0, width):清零输出图像的最后一行,因为最后一行的梯度值未计算。- 返回:
- 函数返回,处理完成。
看看实际运行的效果是什么样子的
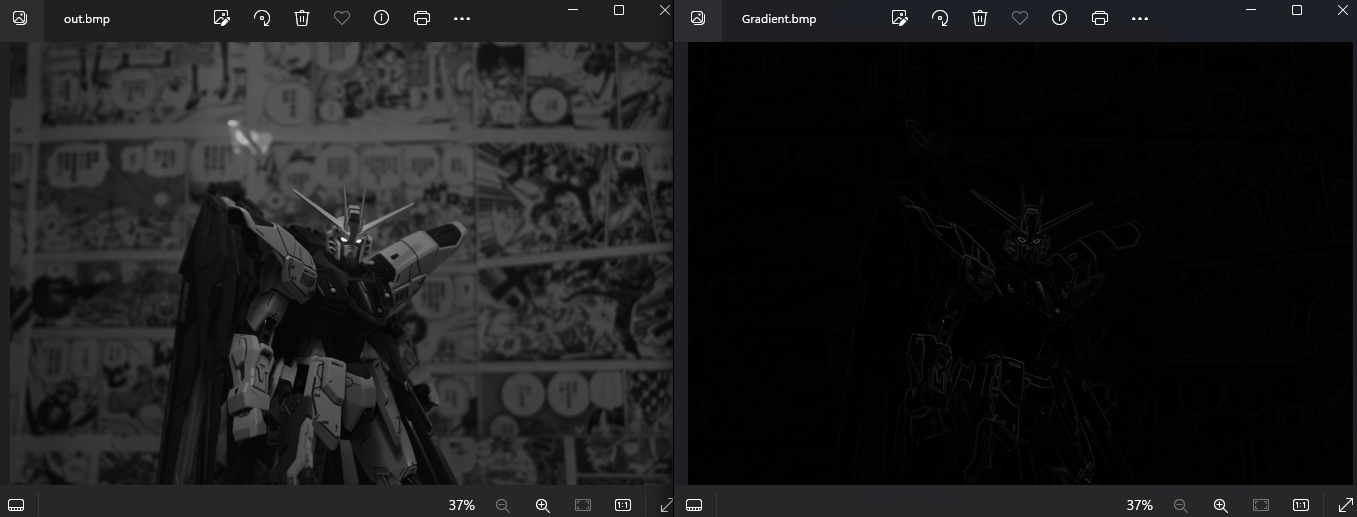
效果并不是很好,我们把原始图像做一下图像增强(灰度值均衡化)试试
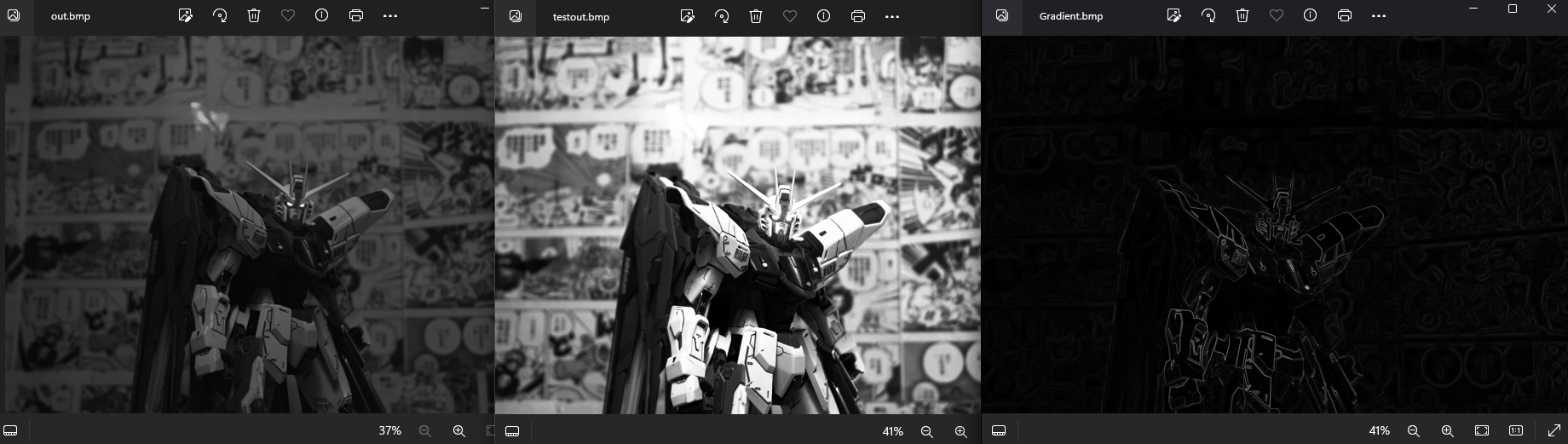
换一种图像增强的方法,加一下反相试试
先简单写一下反相的函数
void invertImage(uint8_t *image, int width, int height) {
for (int i = 0; i < width * height; i++) {
image[i] = 255 - image[i];
}
}
- 1
- 2
- 3
- 4
- 5
这次使用了线性拉伸并简单处理了一下参数
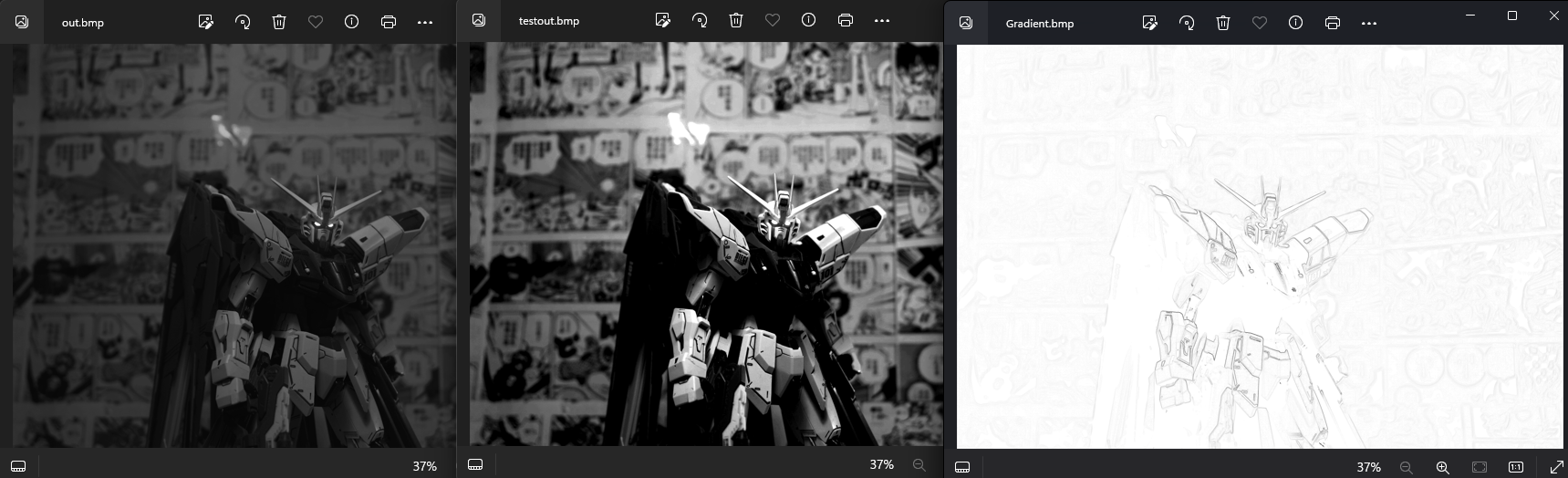
效果还算不错,那如果加一下阈值呢?就像上面说的,我们重新写一下这个函数
//梯度算子加阈值 //pGryImg:输入的灰度图像数据指针。 //width:图像的宽度。 //height:图像的高度。 //pGrdImg:输出的梯度图像数据指针 void RmwGradientGryImgPlus(uint8_t* pGryImg, int width, int height, uint8_t* pGrdImg, int threshold) { uint8_t* pGry, * pGrd; int dx, dy; int x, y; for (y = 0, pGry = pGryImg, pGrd = pGrdImg; y < height - 1; y++) { for (x = 0; x < width - 1; x++, pGry++) { dx = *pGry - *(pGry + 1); dy = *pGry - *(pGry + width); int gradient = (int)(sqrt(dx * dx * 1.0 + dy * dy)); *(pGrd++) = (gradient > threshold) ? min(255, gradient) : 0; } *(pGrd++) = 0; //尾列不做,边缘强度赋0 pGry++; } memset(pGrd, 0, width); //尾行不做,边缘强度赋0 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
看一下效果

画面确实变得更干净了
罗伯特算子
梯度算子的计算只涉及到了3个像素,只在水平和垂直方向做差分。罗伯特算子(Roberts Operator)给出了一个4个像素之间进行运算的算子,分别在两个对角线方向做差分。

由于对角线上2个像素之间的距离为√2,所以罗伯特算子的∆x和∆y采用对角线差分后,不再采用√(∆_x2+∆_y2 ),其描述见下式。罗伯特算子取∆x绝对值与∆y绝对值中的最大值。
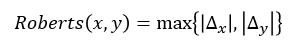
我们来看演示

那么罗伯特算子好在哪呢?
罗伯特算子去掉了梯度算子的开方运算,计算复杂度也降低了不少。
void RmwRobertsGryImg(uint8_t *pGryImg, int width, int height, uint8_t *pRbtImg) { uint8_t *pGry, *pRbt; int dx, dy; int x, y; for (y = 0, pGry = pGryImg, pRbt = pRbtImg; y < height - 1; y++) { for (x = 0; x < width - 1; x++, pGry++) { dx = *pGry - *(pGry + width + 1); dy = *(pGry + 1) - *(pGry + width); *pRbt++ = (uint8_t)(dx > dy ? dx : dy); // 使用三目运算符选择较大的值 } *pRbt++ = 0; // 尾列不做, 边缘强度赋0 pGry++; } memset(pRbt, 0, width); // 尾行不做, 边缘强度赋0 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
我们来看结果
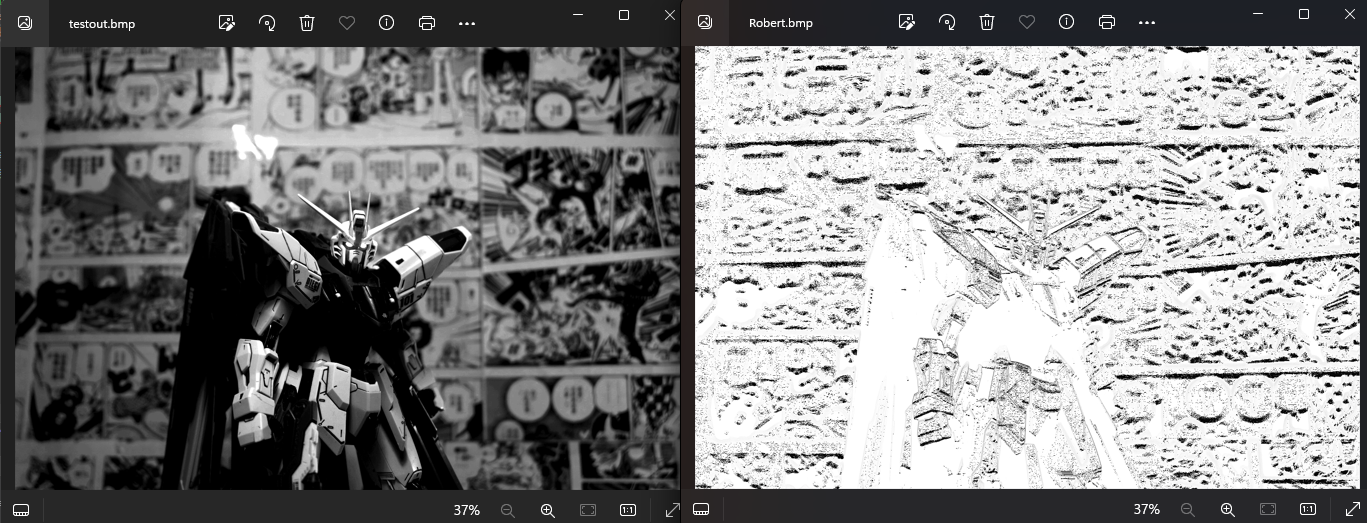
为什么看起来的效果好像还没有梯度算子的结果好呢
是因为图像太复杂没有滤波,那么在边缘计算前能不能先滤波?
我们来看下一个算子
索贝尔算子
在一幅噪声较大的图像中,如果不进行图像平滑就进行边缘检测,必然会在边缘图像中产生噪声干扰。
因此,索贝尔算子(Sobel Operator)中,在求∆x和∆y前,先进行滤波。在求∆x前,先执行如下图的所示的高斯均值滤波;在求∆y前,先执行如下图的所示的高斯均值滤波。

另外,索贝尔算子进一步拉大进行差分的2个像素之间的距离,∆x和∆y采用如下的模板形式

我们来看示意图
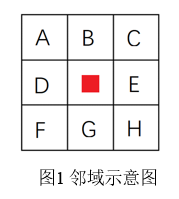
在图像1中,红色方块代表当前像素(x,y),先执行图4-8(a)所示的高斯滤波,用D ̅、E ̅代表滤波后的值,则得到:
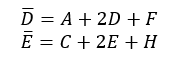
执行∆x模板,则有∆x=D ̅-E ̅=(A+2D+F)-(C+2E+H)
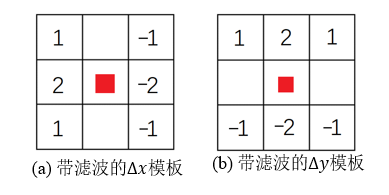
另外,索贝尔算子在对∆x和∆y的使用上,采用了它们的绝对值相加的形式
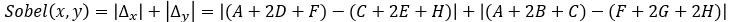
看效果:

对原始灰度图像执行索贝尔算子得到的结果,图中虚线框所示的边缘变成了双线宽。
我们来写代码
//索贝尔算子 void RmwSobelGryImg(uint8_t* pGryImg, int width, int height, uint8_t* pSbImg) { uint8_t* pGry, * pSb; int dx, dy; int x, y; memset(pSbImg, 0, width); // 首行不做, 边缘强度赋0 for (y = 1, pGry = pGryImg + width, pSb = pSbImg + width; y < height - 1; y++) { *pSb++ = 0; // 首列不做, 边缘强度赋0 pGry++; for (x = 1; x < width - 1; x++, pGry++) { // 求dx dx = *(pGry - 1 - width) + (*(pGry - 1) * 2) + *(pGry - 1 + width); dx -= *(pGry + 1 - width) + (*(pGry + 1) * 2) + *(pGry + 1 + width); // 求dy dy = *(pGry - width - 1) + (*(pGry - width) * 2) + *(pGry - width + 1); dy -= *(pGry + width - 1) + (*(pGry + width) * 2) + *(pGry + width + 1); // 结果 *pSb++ = (uint8_t)min(255, abs(dx) + abs(dy)); } *pSb++ = 0; // 尾列不做, 边缘强度赋0 pGry++; } memset(pSb, 0, width); // 尾行不做, 边缘强度赋0 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
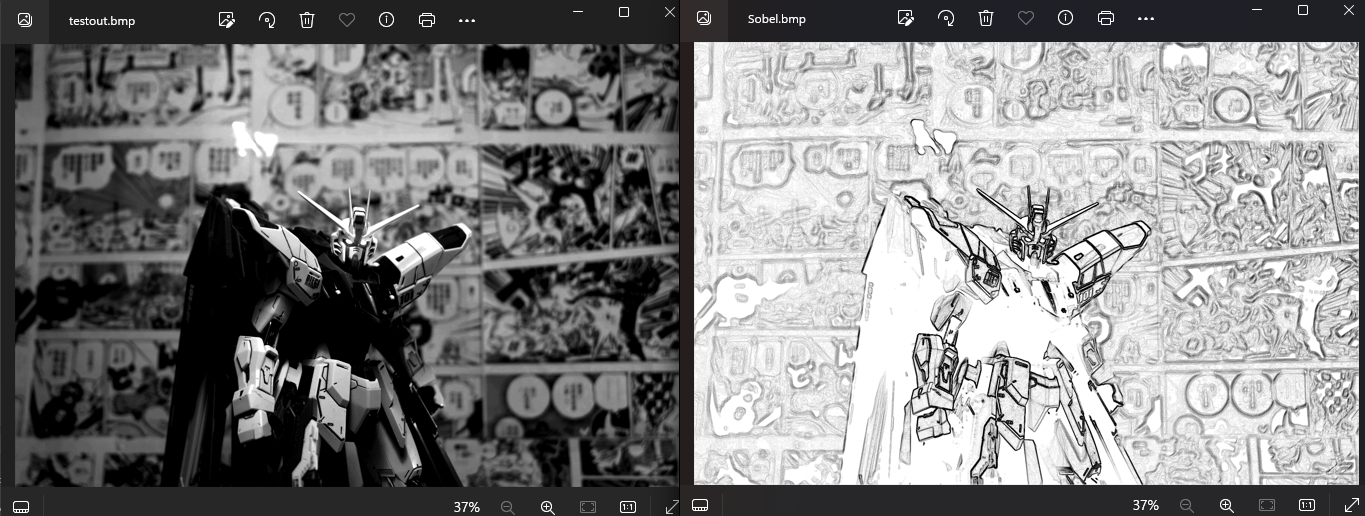
梯度算子、罗伯特算子、索贝尔算子的比较
以下从4个方面对梯度算子、罗伯特算子、索贝尔算子进行比较。
•1. 偏导数∆x和∆y的求取
梯度算子在3个像素之间进行运算,只在水平和垂直方向做差分,做差分的2个像素之间的距离为1。
罗伯特算子在4个像素之间进行运算,分别在两个对角线方向做差分,做差分的2个像素之间的距离为√2。
索贝尔算子在8个像素之间进行运算,只在水平和垂直方向做差分,做差分的2个像素之间的距离为2。
•2. 是否“先平滑后求导”
索贝尔算子在差分之前,进行了加权均值滤波对图像进行平滑(加权函数采用了高斯函数),因此索贝尔具有滤除噪声的效果。梯度算子和罗伯特算子都没有进行平滑。“先平滑后求导”是边缘检测的通用策略,一般在执行梯度算子和罗伯特算子前是需要使用另外的步骤做图像平滑,索贝尔算子则是把平滑写到了算子中。
•3. 边缘强度的大小
按照式(4-4)边缘强度的定义,梯度算子是严格遵守的,罗伯特算子是取∆x绝对值和∆y绝对值中的最大值,索贝尔算子是取∆x与∆y的绝对值之和。而且,索贝尔算子在高斯滤波后没有除以4,所以又相当于∆x、∆y放大了4倍。对于边缘强度,罗伯特算子、梯度算子、索贝尔算子之间的数值关系大致如下:
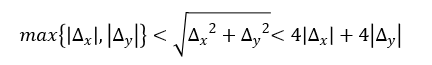
•4. 邻域与边缘宽度
梯度算子、罗伯特算子的计算只涉及到了2行2列,所以它们得到的边缘宽度是1个像素;索贝尔算子涉及到了3行3列,所以它得到的边缘宽度是2个像素,边缘变成了双线宽。
方向模板
若是能根据边缘的具体走向求偏导数,则边缘强度值应该会更准确。
因此在实际应用中,是先假定了有限的几个边缘方向,再对这些假定的每个边缘方向设置一个特定的模板,计算每个模板的边缘强度,从中选择最大的边缘强度作为边缘强度的结果,而且该最大边缘强度对应模板的方向就认为是边缘的方向。
常用基于方向模板的边缘检测算子有:Prewitt算子,Robinson算子、Kirsch算子。Prewitt算子使用4个方向模板,Robinson算子和Kirsch算子都使用8个方向模板。这些算子都是先采用了均值滤波,然后进行差分计算。
Prewitt算子
Prewitt算子设定了0°、45°、90°和135°,共计4种边缘方向;根据这4种边缘方向,分别设计了4个模板
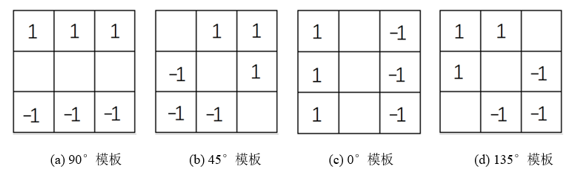
对每个像素分别计算这个4个模板的值,取绝对值最大者作为该像素的边缘强度Prewitt(x,y)。同时该最大值对应模板的方向作为该像素的边缘方向(与边缘的走向相差90°,因为显然边缘走向的法线方向上的导数最大)。若把这些模板中为“0”点(空白处)的连成一条直线,可以发现这些模板强调了水平线、135°斜线、竖直线、45°斜线的检测。Prewitt算子强调对直线的检测,对于上述走向的直线,总有一个模板的输出值最大。
void RmwPrewittGryImg(uint8_t *pGryImg, int width, int height, uint8_t *pPRTImg) { uint8_t *pGry, *pPRT; int dx, dy, d45, d135, v1, v2; int x, y; memset(pPRTImg, 0, width); // 首行不做, 边缘强度赋0 for (y = 1, pGry = pGryImg + width, pPRT = pPRTImg + width; y < height - 1; y++) { *pPRT++ = 0; // 首列不做, 边缘强度赋0 pGry++; for (x = 1; x < width - 1; x++, pGry++) { // 求dx dx = *(pGry - 1 - width) + *(pGry - 1) + *(pGry - 1 + width); dx -= *(pGry + 1 - width) + *(pGry + 1) + *(pGry + 1 + width); // 求dy dy = *(pGry - width - 1) + *(pGry - width) + *(pGry - width + 1); dy -= *(pGry + width - 1) + *(pGry + width) + *(pGry + width + 1); // 求45度 d45 = *(pGry - width - 1) + *(pGry - width) + *(pGry - 1); d45 -= *(pGry + width + 1) + *(pGry + width) + *(pGry + 1); // 求135度 d135 = *(pGry - width) + *(pGry - width + 1) + *(pGry + 1); d135 -= *(pGry + width - 1) + *(pGry + width) + *(pGry - 1); // 结果 v1 = abs(dx) > abs(dy) ? abs(dx) : abs(dy); v2 = abs(d45) > abs(d135) ? abs(d45) : abs(d135); *pPRT++ = (uint8_t)((v1 > v2) ? ((v1 > 255) ? 255 : v1) : ((v2 > 255) ? 255 : v2)); } *pPRT++ = 0; // 尾列不做, 边缘强度赋0 pGry++; } memset(pPRT, 0, width); // 尾行不做, 边缘强度赋0 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
我们看一下实现效果
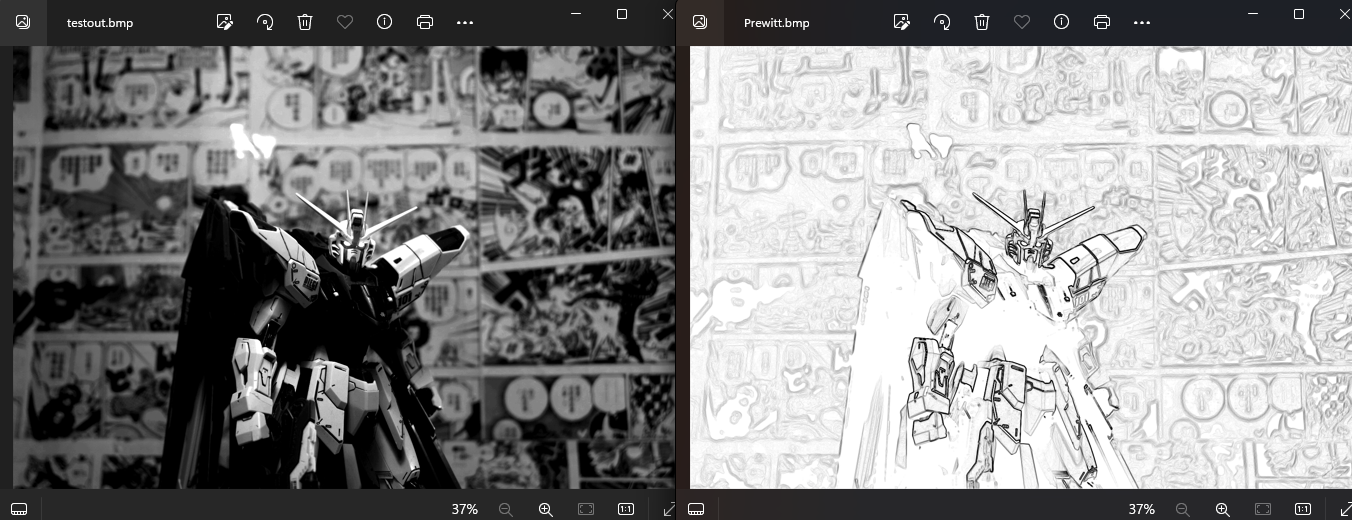
Robinson算子
Robinson算子除(a)外的7个模板,都是由其上个模板顺时针旋转1个像素得到的。若是把模板中的负数值合并成一个区域,可以看出该算子强调了对角点的检测;对于各种形状的角点,总有一个模板的输出值最大。
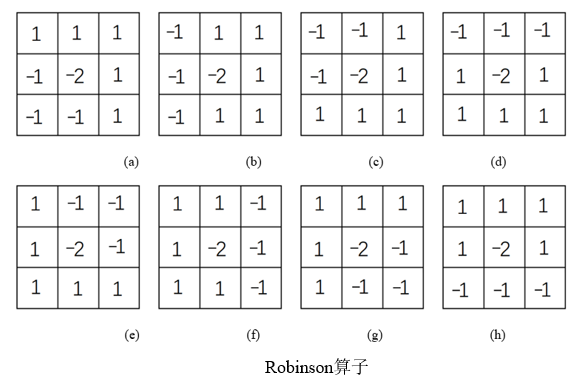
有兴趣大家可以查一下啊,这里就不再过多解释
二阶微分算子
一阶微分算子能够得到边缘强度,但是需要再加上一定的条件约束,比如设置个阈值,才能判定一个像素是不是边缘点。
通过对边缘类型及其导数的分析可知,阶跃边缘的导数特征除了“一阶导数取极值”外,还有“二阶导数过零点”。因此可以采用二阶导数,利用过零点得到边缘点,这样就不需要其他的条件了。
拉普拉斯算子
拉普拉斯算子(Laplacian Operator)是近似给出二阶导数的流行方法,其使用3×3的邻域,给出了4-邻接和8-邻接的邻域的2种模板
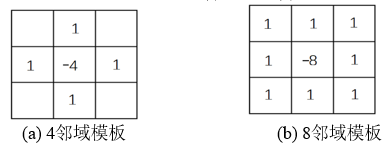
对如图所示的原始灰度图像执行4邻域拉普拉斯算子,得到的结果如图所示,图中虚线框所示的位置上发生了过零点(导数由负数变到了正数),此处即边缘。
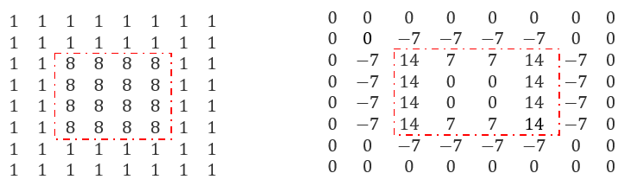
在拉普拉斯算子的结果图像中,可以发现过零点位置刚好就是边缘的位置。由于过零点是在像素之间,不在整数坐标上,所以在提取边缘点时,往往采取下面的策略:
当一个像素的二阶导数大于0,其邻域内有像素的二阶导数小于0或等于0,则该像素被标记为边缘点。
沈俊算子
唯一一个以国人命名的算子
沈俊教授同样提出了先滤波后求导的边缘检测方法(J. Shen and S. Castan, An optimal linear operator for step edge detection, CVGIP: Graphical Models and Image Processing, Vol. 54 No.2, Mar. 1992, pp.112 – 133),即沈俊算子(ShenJun Edge Operator)。
沈教授在阶跃边缘和可加白噪声模型下,就信噪比最大准则,证明了图像平滑的最佳滤波器是对称的指数函数,形式如下:
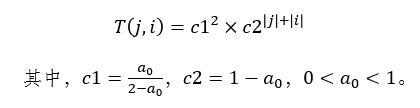
显然,当a_0越大时,c2就越小,T(j,i)就越陡越窄,相当于滤波邻域就越小,压制噪声的能力就弱,图像模糊程度就越小,边缘定位的精度就越高。
在算子实现上,沈教授对图像分别按行、按列各进行两次先正方向再反方向的递推滤波实现(|j|、|i|的优点),等价于用上述指数函数进行图像滤波;证明了滤波结果减去原始灰度值得到的差值乘以2c1〖ln〗^c2,约等于其二阶导数的值。沈俊算子的实现过程如下:
沈俊算子的实现过程
step.1 对每行从左向右进行:
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/笔触狂放9/article/detail/473266推荐阅读相关标签Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。



