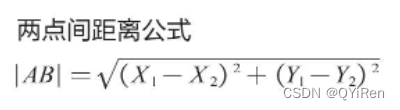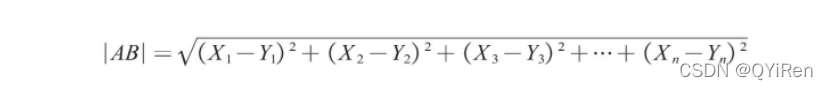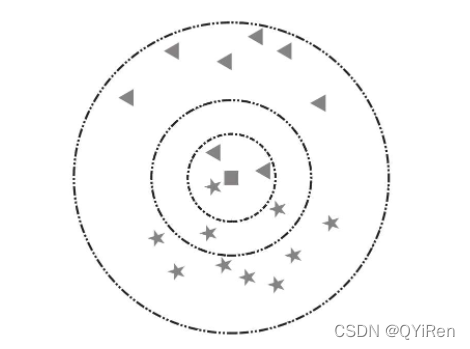
（K的含义）以下图为例，假设五角星代表爱情片，三角形代表科幻片。此时加入一个新样本正方形，需要判断其类别。当选择以离新样本最近的3个近邻点（K＝3）为判断依据时，这3个点由1个五角星和2个三角形组成，根据“少数服从多数”原则，可以认为新样本属于三角形的类别，即新样本是一部科幻片。同理，当选择离新样本最近的5个近邻点（K＝5）为判断依据时，这5个点由3个五角星和2个三角形组成，根据“少数服从多数”原则，可以认为新样本属于五角星的类别，即新样本是一部爱情片。

如何判断2个数据的相似度或者说2个数据之间的距离？这里以最为常见的欧式距离来定义向量空间中2个点的距离。如下是适用于两个特征变量的情况。

实际应用中，数据的特征通常有n个，此时可将该距离公式推广到n维空间，如n维向量空间内A点坐标为（X1，X2，X3，…，Xn），B点坐标为（Y1，Y2，Y3，…，Yn），那么A、B两点间的欧氏距离计算公式如下。

2 算法计算步骤

这里通过一个简单的例子“如何判断葡萄酒的种类”来讲解K近邻算法的计算步骤。

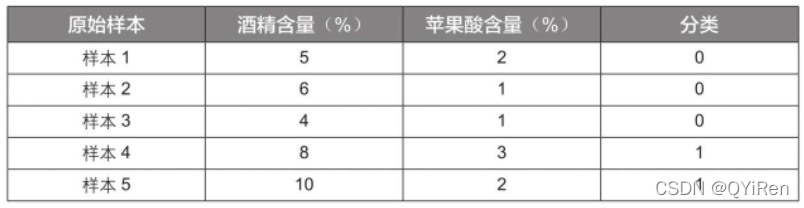
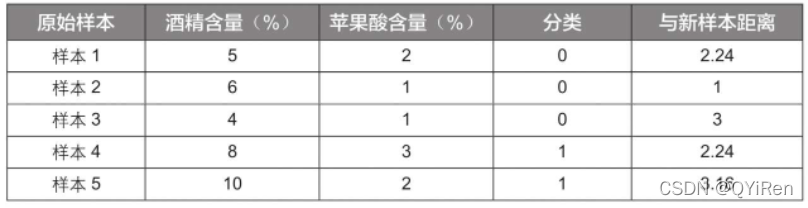
商业实战中用于评判葡萄酒的指标有很多，为方便演示，这里只根据“酒精含量”和“苹果酸含量”2个特征变量将葡萄酒分为2类，并且原始样本数据只有5组，见下表。（数据已经经过数据预处理标准化，后序将会详细介绍数据预处理相关）

“分类”取值为0代表葡萄酒A，取值为1代表葡萄酒B。

现在需要使用K近邻算法对一个新样本进行分类，该新样本的特征数据见下表，那么这个新样本是属于葡萄酒A还是葡萄酒B呢？

此时可以利用距离公式来计算新样本与已有样本之间的距离，即不同样本间的相似度。结果见下表。

如果令K值等于1，也就是以离新样本最近的原始样本的种类作为新样本的种类，此时新样本离样本2最近，则新样本的分类为0，也就是葡萄酒A。

如果令K值等于3，也就是以离新样本最近的3个原始样本的多数样本的种类为判断依据，此时最近的3个原始样本是样本2、样本1、样本4，它们中以分类0居多，所以判定新样本的分类为0，也就是葡萄酒A。

3 代码实现


import pandas as pd
from sklearn.neighbors import KNeighborsClassifier as KNN
 
# 导入数据
df = pd.read_excel('葡萄酒.xlsx')
X_train = df[['酒精含量(%)','苹果酸含量(%)']]
y_train = df['分类']
 
# 模型拟合，K值为3
knn = KNN(n_neighbors=3)
knn.fit(X_train,y_train)
 
# 模型预测
X_test = [[7,1]]
knn.predict(X_test)
# 输出：array([0], dtype=int64)
 
# 预测多个样本
X_test = [[7,1],[8,3]]
knn.predict(X_test)
# 输出：array([0, 1], dtype=int64)

补充知识点：K近邻算法回归模型

前面的代码是用K近邻算法中的K近邻算法分类模型（KNeighborsClassifier）进行分类分析，K近邻算法还可以做回归分析，对应的模型为K近邻算法回归模型（KNeighborsRegressor）。K近邻算法分类模型将离待预测样本点最近的K个训练样本点中出现次数最多的分类作为待预测样本点的分类，K近邻算法回归模型则将离待预测样本点最近的K个训练样本点的平均值作为待预测样本点的分类。


from sklearn.neighbors import KNeighborsRegressor
X = [[1,2],[3,4],[5,6],[7,8],[9,10]]
y = [1,2,3,4,5]
model = KNeighborsRegressor(n_neighbors=2)
model.fit(X,y)
model.predict([[5,5]])
# 输出：array([2.5])

4 案例：手写数字识别模型

4.1 手写数字识别原理

手写数字识别，或者说图像识别的本质就是把一张图片转换成计算机能够处理的数字形式。

4.1.1 图像二值化

如下图所示是将图片格式的数字4转换成由0和1组成的“新的数字4”。这是一个32×32的矩阵，数字1代表有颜色的地方，数字0代表无颜色的地方，这样就完成了手写数字识别的第一步也是最关键的一步：将图片转换为计算机能识别的内容——数字0和1。这个步骤又称为图像二值化，将在后序介绍。

4.1.3 距离计算

手写数字图片处理后形成的1×1024的二维数组可以看成一个行向量，两张图片对应的行向量间的欧氏距离可以反映两张图片的相似度。因此，可以利用K近邻算法模型计算新样本与原始训练集中各个样本的欧氏距离，取新样本的K个近邻点，并以大多数近邻点所在的分类作为新样本的分类。

根据KNN原理，对于一个新样本，我们可以计算它与每个不同样本数字之间的距离，再根据与其距离最近的K个近邻点判别其属于哪个分类，即哪个数字。

4.2 代码实现

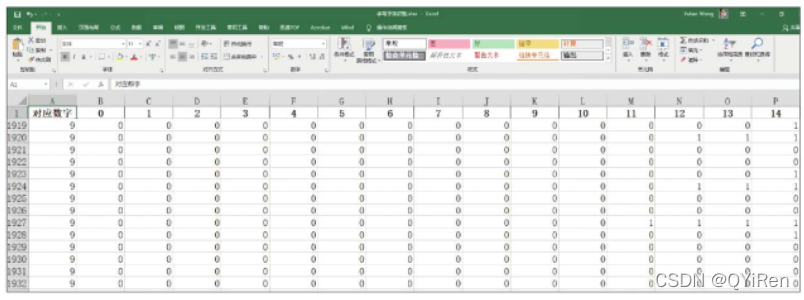
数据集如下图所示：该数据集为1934个处理好的手写数字0～9的1×1024矩阵，其中每一行为一个手写数字，第1列“对应数字”为该手写数字，其余每一列为该手写数字对应的1×1024矩阵中的一个数字。


import pandas as pd
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
 
# 导入数据,提取特征变量与目标变量
df = pd.read_excel('手写字体识别.xlsx')
X = df.drop(columns=['对应数字'])
y = df['对应数字']
 
# 划分训练集与测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123)
 
# 模型搭建
knn = KNN(n_neighbors=5)
knn.fit(X_train,y_train)
 
# 模型预测
y_pred = knn.predict(X_test)
 
# 测试集预测结果与实际结果对比
a = pd.DataFrame()
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)
 
# 模型评估
accuracy = accuracy_score(y_pred,y_test)
# 或者模型自带函数model.score(X_test,y_test),注意两个函数的参数不一样

引入交叉验证和网格搜索：


from sklearn.model_selection import GridSearchCV
parameters = {'n_neighbors':[1,2,3,4,5,6,7,8]}
knn = KNN()
grid_search = GridSearchCV(knn,parameters,cv=5)
# 以准确度为基础进行网格搜索，寻找最优参数
grid_search.fit(X_train,y_train)
grid_search.best_params_

5 图像识别原理简介

本节讲解在Python中如何对一张图片进行简单处理，使其变成计算机能识别的内容。

5.1 图片大小调整及显示

Pillow库是一款功能强大、简单好用的第三方图像处理库。


# 引入Pillow库中的Image模块来处理图像
from PIL import Image
 
# open()函数可以打开JPG、PNG等格式的图片
img = Image.open('数字4.png')
 
# resize()函数可以调整图像大小，这里调整为32×32像素
img = img.resize((32,32))
 
img.show()

结果如下图所示。

5.2 图像灰度处理

原始图片是一个彩色的数字4，我们需要对其进行灰度处理，将其转换为黑白的数字4，以便之后将其转换为数字0和1，代码如下。

img = img.convert('L')

5.3 图片二值化处理

获得黑白的数字4后，就要进行关键的图像二值化处理了，代码如下。


import numpy as np
img_new = img.point(lambda x:0 if x > 128 else 1)
arr = np.array(img_new)

point()函数可以操控每一个像素点，point()函数中传入的内容为之前讲pandas库时讲过的lambda匿名函数，其含义为将色彩数值大于128的像素点赋值为0，反之赋值为1。

图像在进行灰度处理后，每一个像素点由一个取值范围为0～255的数字表示，其中0代表黑色，255代表白色，所以这里以128为阈值进行划分，即原来偏白色的区域赋值为0，原来偏黑色的区域赋值为1。这样便完成了将颜色转换成数字0和1的工作。

array()函数将已经转换成数字0和1的32×32像素的图片转换为32×32的二维数组，并赋给变量arr。


for i in range(arr.shape[0]):
    print(arr[i])

打印所有行，一共32行。

5.4 将二维数组转换为一维数组

上面获得的32×32的二维数组不能用于数据建模，因此还需要用reshape（1,-1）函数将其转换成一行（若写成reshape（-1,1）则转换成一列），即1×1024的一维数组，代码如下。

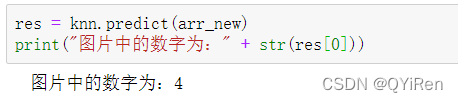
把处理好的一维数组arr_new传入前面训练好的knn模型中，代码如下。

因为获取到的res是一个一维数组（类似列表），所以通过res[0]提取其中的元素，又因为提取出的元素是数字，不能直接进行字符串拼接，所以用str()函数转换后再进行字符串拼接，运行结果如下，可以看到，预测结果是正确的。

手写数字识别完整代码（单图）


# 主要分为3步：第1步训练模型，第2步处理图片，第3步进行预测
 
# 第1步 训练模型
# 1.读取数据
import pandas as pd
df = pd.read_excel('手写字体识别.xlsx')
 
# 2.提取特征变量和目标变量
X = df.drop(columns=['对应数字'])
y = df['对应数字']
 
# 3.划分训练集与测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123)
 
# 4.搭建并训练模型
from sklearn.neighbors import KNeighborsClassifier as KNN
knn = KNN(n_neighbors=5)
knn.fit(X_train,y_train)
 
# 第2步 处理图片
# 1.图片读取，大小调整，灰度处理
from PIL import Image
img = Image.open('数字8.jpg')
img = img.resize((32,32))
img = img.convert('L')
 
# 2.图片二值化，二维数组转一维数组
import numpy as np
img_new = img.point(lambda x:0 if x > 128 else 1)
arr = np.array(img_new)
arr_new = arr.reshape(1,-1)
 
# 第3步 预测
res = knn.predict(arr_new)
print('图片中的数字为：' + str(res[0]))

参考书籍

《Python大数据分析与机器学习商业案例实战》

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/549055