devbox
笔触狂放9
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Java数据结构之栈详解_java中的栈

作者：笔触狂放9 | 2024-05-23 07:08:33

赞

踩

java中的栈

栈的定义：

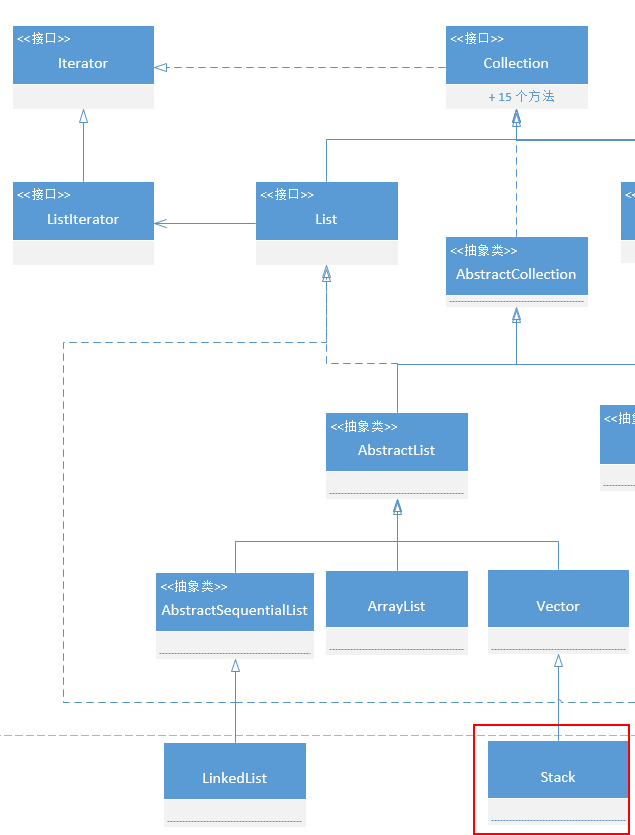
栈（stack）是一种用于存储数据的简单数据结构。栈一个有序线性表，只能在表的一端（PS：栈顶）执行插人和删除操作。最后插人的元素将被第一个删除。所以，栈也称为后进先出（Last In First Out,LIFO）或先进后出（First In Last Out,FILO）线性表。

这里写图片描述

 

Java 集合框架中的 Stack 继承自 Vector：

  • 由于 Vector 有 4 个构造函数，加上 Stack 本身的一种，也就是说有 5 中创建 Stack 的方法
  • 跟 Vector 一样，它是可以由数组实现的栈。

栈的几种主要基本操作：

  • void push(int data)：入栈（将数据data插入到栈中）
  • int pop()：出栈（删除并返回最后一个插入栈的元素）
  • int top()：返回最后一个插入栈的元素，但不删除
  • int size()：返回存储在栈中的元素个数
  • boolean isEmpty()：返回栈是否是空栈
  • boolean isFull()：返回是否是满栈
  • void Clear()：清除整个栈

栈的应用：

  • 符号匹配
  • HTML和XML文件中的标签匹配（实质还是符号匹配）
  • 实现函数调用
  • 文本编辑器中的撤销
  • 网页浏览器中已访问页面的历史记录
  • 作为一个算法的辅助数据结构

栈的基本方法：

  1. public interface Stack<E> extends Iterable<E> {
  2.     
  3.     //获取栈的size大小
  4.     public int size();
  5.     
  6.     //判断栈是否为空
  7.     public boolean isEmpty();
  8.  
  9.     //入栈 进栈一个元素 在线性表的表尾添加一个元素
  10.     public void push(E element);
  11.  
  12.     //出栈 弹出一个元素 在线性表的表尾删除一个元素
  13.     public E pop();
  14.  
  15.     //查看当前栈顶元素 并不是移除 查看线性表中最后一个元素
  16.     public E peek();
  17.  
  18.     //对当前栈进行清空
  19.     public void clear();
  20. }

栈的几种实现方式

  1. 基于简单数组的实现方式
  2. 基于动态数组的实现方式
  3. 基于链表的实现方式
  4. 基于队列的实现方式

1.基于简单数组的实现：

        基于简单数组实现一个栈，其基本思路是这样的：从左至右向数组中添加所有的元素，并定义一个变量用来记录数组当前栈顶(top)元素的下标。当数组存满了栈元素时，执行入栈(插入元素)操作将抛出栈满异常；当对一个没有存储栈元素的数组执行出栈(删除元素)操作将抛出栈空异常，当然，这种实现方式有一个很明显的局限性。那就是：栈的最大空间必须预先声明且不能改变。试图对一个满栈执行入栈操作将会产生异常。

2.基于动态数组的实现：

        基于动态数组的实现一个栈，其基本思路跟上面类似。不同的是，这种方式下当数组中存储的元素达到一定量时（如：数组空间的0.75或者整个数组空间），这时我们通常会选择新建一个比原数组空间大一倍的新数组，然后将原数组按照原来的顺序复制进去，接着便可以继续进行入栈操作了。

  1. import p1.Stack;（上方的Stack包）
  2.  
  3. import java.util.Iterator;
  4.  
  5. public class ArrayStack<E> implements Stack<E> {
  6.     
  7.     //定义私有变量List
  8.     private ArrayList<E> list;
  9.     
  10.     //默认构造
  11.     public ArrayStack() {
  12.         list = new ArrayList<>();
  13.     }
  14.     //自己定义数组长度
  15.     public ArrayStack(int capacity) {
  16.         list = new ArrayList<>(capacity);
  17.     }
  18.     
  19.     //size实现
  20.     @Override
  21.     public int size() {
  22.         return list.size();
  23.     }
  24.     //判空实现
  25.     @Override
  26.     public boolean isEmpty() {
  27.         return list.isEmpty();
  28.     }
  29.     //push方法
  30.     @Override
  31.     public void push(E element) {
  32.         list.add(element);
  33.     }
  34.     //pop方法实现
  35.     @Override
  36.     public E pop() {
  37.         return list.remove(list.size() - 1);
  38.     }
  39.     //peek实现
  40.     @Override
  41.     public E peek() {
  42.         return list.get(list.size() - 1);
  43.     }
  44.     //clear方法
  45.     @Override
  46.     public void clear() {
  47.         list.clear();
  48.     }
  49.     //迭代方法
  50.     @Override
  51.     public Iterator<E> iterator() {
  52.         return list.iterator();
  53.     }
  54.     //toString方法实现
  55.     @Override
  56.     public String toString() {
  57.         return list.toString();
  58.     }
  59.     //继承Object equals方法
  60.     @Override
  61.     public boolean equals(Object o) {
  62.         if (o == null) {
  63.             return false;
  64.         }
  65.         if (this == o) {
  66.             return true;
  67.         }
  68.         if (o instanceof ArrayStack) {
  69.             ArrayStack other = (ArrayStack) o;
  70.             return this.list.equals(other.list);
  71.         }
  72.         return false;
  73.     }
  74. }

3.基于链表的实现:

        基于链表实现一个栈，其基本思路是这样的：通过在链表的表头插入元素的方式来实现push操作；通过删除链表的表头节点的方式来实现pop操作.

  1. public class SinglyNode<K extends Object> {
  2.     private K data; // 数据
  3.     private SinglyNode<K> next; // 该节点的下个节点
  4.  
  5.     public SinglyNode(K data) {
  6.         this.data = data;
  7.     }
  8.  
  9.     public SinglyNode(K data, SinglyNode<K> next) {
  10.         this.data = data;
  11.         this.next = next;
  12.     }
  13.  
  14.     public K getData() {
  15.         return data;
  16.     }
  17.  
  18.     public void setData(K data) {
  19.         this.data = data;
  20.     }
  21.  
  22.     public SinglyNode<K> getNext() {
  23.         return next;
  24.     }
  25.  
  26.     public void setNext(SinglyNode<K> next) {
  27.         this.next = next;
  28.     }
  29.  
  30.     @Override
  31.     public String toString() {
  32.         return "SinglyNode [data=" + data + "]";
  33.     }
  34.  
  35. }
  1. public class LinkStack<K extends Object> implements Stack<K> {
  2.  
  3.     private SinglyNode<K> headNode;
  4.     //是否为满栈
  5.     public boolean isFull() {
  6.         return false;
  7.     }
  8.     //是否为空
  9.     public boolean isEmpty(){
  10.         return headNode == null ? true : false;
  11.     }
  12.     
  13.     
  14.     //入栈
  15.     public void push(K data){
  16.         if(headNode == null){
  17.             headNode = new SinglyNode<K>(data);
  18.         }else{
  19.             SinglyNode<K> newNode = new SinglyNode<K>(data);
  20.             newNode.setNext(headNode);
  21.             headNode = newNode;
  22.         }
  23.     }
  24.     
  25.     //出栈
  26.     public K pop(){
  27.         if(headNode == null){
  28.             throw new EmptyStackException();
  29.         }else{
  30.             K data = headNode.getData();
  31.             headNode = headNode.getNext();
  32.             return data;
  33.         }
  34.     }
  35.     
  36.     //返回栈顶元素
  37.     public K top(){
  38.         if(headNode == null){
  39.             throw new EmptyStackException();
  40.         }else{
  41.             return headNode.getData();
  42.         }
  43.     }
  44.     
  45.     //返回栈中元素个数
  46.     public int size(){
  47.         if(headNode == null){
  48.             return 0;
  49.         }else{
  50.             int length = 0;
  51.             SinglyNode<K> currentNode = headNode;
  52.             while (currentNode != null) {
  53.                 length++;
  54.                 currentNode = currentNode.getNext();
  55.             }
  56.             return length;
  57.         }
  58.     }
  59.     
  60.     //清空栈
  61.     public void ClearStack(){
  62.         headNode = null;
  63.     }
  64.  
  65.    //遍历栈从前往后
  66.     @Override
  67.     public void print() {
  68.         SinglyNode<K> tmpNode = headNode;
  69.         printFromEnd(tmpNode);
  70.     }
  71.     
  72.     //遍历栈从后往前
  73.     public void printFromEnd(SinglyNode<K> headNode){
  74.         if(headNode != null){
  75.             if(headNode.getNext() != null){
  76.                 printFromEnd(headNode.getNext());
  77.             }
  78.             
  79.             System.out.print(headNode.getData() + " ");
  80.         }
  81.     }
  82.  
  83. }

 基于数组实现和基于链表实现的比较

（1）基于数组实现的栈：

  • 各个操作都是常数时间开销
  • 每隔一段时间进行的倍增操作的时间开销较大

（2）基于链表实现的栈：

  • 栈规模的增加和减小都很容易
  • 各个操作都是常数时间开销
  • 每个操作都需要使用额外的空间和时间开销来处理指针

4.基于队列实现栈：

  1. import java.util.Iterator;
  2.  
  3. //队列实现栈
  4. public class QueueToStack {
  5.     public static void main(String[] args) {
  6.         StackImplByQueue<Integer> stack = new StackImplByQueue<>();
  7.         System.out.println(stack);
  8.         for (int i = 1; i <= 5; i++) {
  9.             stack.push(i); //队列A
  10.         }
  11.         System.out.println(stack.toString());
  12.         System.out.println(stack.pop());
  13.         System.out.println(stack);  //队列B
  14.  
  15.     }
  16. }
  17.  
  18. class StackImplByQueue<E> implements Stack<E> { //上方的栈调用
  19.     private ArrayQueue<E> queueA;
  20.     private ArrayQueue<E> queueB;
  21.  
  22.     public StackImplByQueue() {
  23.         queueA = new ArrayQueue<>();
  24.         queueB = new ArrayQueue<>();
  25.     }
  26.  
  27.     @Override
  28.     public int size() {
  29.         if (queueA.isEmpty() && queueB.isEmpty()) {
  30.             return 0;
  31.         } else if (!queueA.isEmpty()) {
  32.             return queueA.size();
  33.         } else {
  34.             return queueB.size();
  35.         }
  36.     }
  37.  
  38.     @Override
  39.     public boolean isEmpty() {
  40.         return queueA.isEmpty() && queueB.isEmpty();
  41.     }
  42.  
  43.     @Override
  44.     public void push(E element) {
  45.         if (queueA.isEmpty() && queueB.isEmpty()) {
  46.             queueA.offer(element);
  47.         } else if (!queueA.isEmpty()) {
  48.             queueA.offer(element);
  49.         } else {
  50.             queueB.offer(element);
  51.         }
  52.     }
  53.  
  54.     @Override
  55.     public E pop() {
  56.         if (isEmpty()) {
  57.             return null;
  58.         }
  59.         E ret = null;
  60.         if (!queueA.isEmpty()) {
  61.             while (queueA.size() != 1) {
  62.                 queueB.offer(queueA.poll());
  63.             }
  64.             ret = queueA.poll();
  65.         } else {
  66.             while (queueB.size() != 1) {
  67.                 queueA.offer(queueB.poll());
  68.             }
  69.             ret = queueB.poll();
  70.         }
  71.         return ret;
  72.     }
  73.  
  74.     @Override
  75.     public E peek() {
  76.         if (isEmpty()) {
  77.             return null;
  78.         }
  79.         E ret = null;
  80.         if (!queueA.isEmpty()) {
  81.             while (queueA.size() != 1) {
  82.                 queueB.offer(queueA.poll());
  83.             }
  84.             ret = queueA.poll();
  85.             queueB.offer(ret);
  86.         } else {
  87.             while (queueB.size() != 1) {
  88.                 queueA.offer(queueB.poll());
  89.             }
  90.             ret = queueB.poll();
  91.             queueA.offer(ret);
  92.         }
  93.         return ret;
  94.     }
  95.  
  96.     @Override
  97.     public void clear() {
  98.         queueA.clear();
  99.         queueB.clear();
  100.     }
  101.  
  102.     @Override
  103.     public Iterator<E> iterator() {
  104.         if (isEmpty()) {
  105.             return queueA.iterator();
  106.         } else if (!queueA.isEmpty()) {
  107.             return queueA.iterator();
  108.         } else {
  109.             return queueB.iterator();
  110.         }
  111.     }
  112.     @Override
  113.     public String toString() {
  114.         if (isEmpty()) {
  115.             return "[]";
  116.         } else if (!queueA.isEmpty()) {
  117.             return queueA.toString();
  118.         } else {
  119.             return queueB.toString();
  120.         }
  121.     }
  122.  
  123. }

Java 集合框架中的 Stack 具有以下特点：

  • 继承自 Vector
  • 有 5 种创建 Stack 的方法
  • 采用数组实现
  • 除了 push()，剩下的方法都是同步的。

双端栈：

        双端栈定义：

                是指一个线性表的两端当做栈底，分别进行入栈和出栈操作，主要利用了栈：栈底不变，栈顶变化的特征；

        

        双端栈是线性表的一种,更是栈的一个特殊分类，可用借用动态数组+栈的组合实现。

 

 双端栈实现方法以及基本方法：

  1. import java.util.Iterator;
  2.     //双端栈
  3. public class ArrayDoubleEndStack<E> implements Iterable<E> {
  4.     //左端栈的栈顶
  5.     private int ltop;
  6.     //右端栈的栈顶
  7.     private int rtop;
  8.     //存储元素的容器
  9.     private E[] data;
  10.     //数组容器的默认容量
  11.     private static int DEFAULT_CAPACITY = 10;
  12.     //构造
  13.     public ArrayDoubleEndStack() {
  14.         data = (E[]) new Object[DEFAULT_CAPACITY];
  15.         ltop = -1;
  16.         rtop = data.length;
  17.     }
  18.     //左入栈
  19.     public void pushLeft(E element) {
  20.         if (ltop + 1 == rtop) {
  21.             resize(data.length * 2);
  22.         }
  23.         data[++ltop] = element;
  24.     }
  25.     //右入栈
  26.     public void pushRight(E element) {
  27.         if (ltop + 1 == rtop) {
  28.             resize(data.length * 2);
  29.         }
  30.         data[--rtop] = element;
  31.     }
  32.     //扩容
  33.     private void resize(int newLen) {
  34.         E[] newData = (E[]) new Object[newLen];
  35.         //复制左端栈的元素
  36.         for (int i = 0; i <= ltop; i++) {
  37.             newData[i] = data[i];
  38.         }
  39.         //复制右端栈的元素
  40.         int index = rtop;
  41.         for (int i = newLen - sizeRight(); i < newLen; i++) {
  42.             newData[i] = data[index++];
  43.         }
  44.         rtop = newLen - sizeRight();
  45.         data = newData;
  46.     }
  47.     //左出栈
  48.     public E popLeft() {
  49.         if (isLeftEmpty()) {
  50.             throw new IllegalArgumentException("left stack is null");
  51.         }
  52.         E ret = data[ltop--];
  53.         if (sizeLeft() + sizeRight() <= data.length / 4 && data.length > DEFAULT_CAPACITY) {
  54.             resize(data.length / 2);
  55.         }
  56.         return ret;
  57.     }
  58.     //右出栈
  59.     public E popRight() {
  60.         if (isRightEmpty()) {
  61.             throw new IllegalArgumentException("right stack is null");
  62.         }
  63.         E ret = data[rtop++];
  64.         if (sizeLeft() + sizeRight() <= data.length / 4 && data.length > DEFAULT_CAPACITY) {
  65.             resize(data.length / 2);
  66.         }
  67.         return ret;
  68.     }
  69.     //获取左栈顶
  70.     public E peekLeft() {
  71.         if (isLeftEmpty()) {
  72.             throw new IllegalArgumentException("left stack is null");
  73.         }
  74.         return data[ltop];
  75.     }
  76.     //获取右栈顶
  77.     public E peekRight() {
  78.         if (isRightEmpty()) {
  79.             throw new IllegalArgumentException("right stack is null");
  80.         }
  81.         return data[rtop];
  82.     }
  83.     
  84.     //判断是否左边为空
  85.     public boolean isLeftEmpty() {
  86.         return ltop == -1;
  87.     }
  88.     //判断是否右边为空
  89.     public boolean isRightEmpty() {
  90.         return rtop == data.length;
  91.     }
  92.     //通过左指针获取长度
  93.     public int sizeLeft() {
  94.         return ltop + 1;
  95.     }
  96.     //通过右指针获取长度
  97.     public int sizeRigh() {
  98.         return data.length - rtop;
  99.     }
  100.     //重写toString方法
  101.     @Override
  102.     public String toString() {
  103.         StringBuilder sb = new StringBuilder();
  104.         sb.append('[');
  105.         if (isLeftEmpty() && isRightEmpty()) {
  106.             sb.append(']');
  107.             return sb.toString();
  108.         }
  109.         //先左边
  110.         for (int i = 0; i <= ltop; i++) {
  111.             sb.append(data[i]);
  112.             if (i == ltop && isRightEmpty()) {
  113.                 sb.append(']');
  114.                 return sb.toString();
  115.             } else {
  116.                 sb.append(',');
  117.             }
  118.         }
  119.         //后右边
  120.         for (int i = rtop; i < data.length; i++) {
  121.             sb.append(data[i]);
  122.             if (i == data.length - 1) {
  123.                 sb.append(']');
  124.             } else {
  125.                 sb.append(',');
  126.             }
  127.         }
  128.         return sb.toString();
  129.     }
  130.     //迭代器
  131.     @Override
  132.     public Iterator<E> iterator() {
  133.         return new ArrayDoubleEndStackIterator();
  134.     }
  135.  
  136.     class ArrayDoubleEndStackIterator implements Iterator<E> {
  137.         private ArrayList<E> list;
  138.         private Iterator<E> it;
  139.         public ArrayDoubleEndStackIterator() {
  140.             list = new ArrayList<>();
  141.             for (int i = 0; i <= ltop; i++) {
  142.                 list.add(data[i]);
  143.             }
  144.             for (int i = rtop; i < data.length; i++) {
  145.                 list.add(data[i]);
  146.             }
  147.             it = list.iterator();
  148.         }
  149.  
  150.         @Override
  151.         public boolean hasNext() {
  152.             return it.hasNext();
  153.         }
  154.  
  155.         @Override
  156.         public E next() {
  157.             return it.next();
  158.         }
  159.     }
  160. }

双端栈的扩容与缩容问题；

        双端栈A中有下标0-5的6个元素，对其进行扩容；

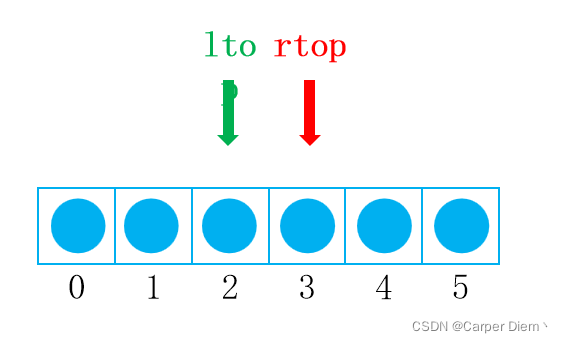
         对其扩容时候，先考虑左边，从原来双端栈A的左边原封不动直接进入双端栈B，此时与双端栈A的左指针相同，皆为下标2，此时双端栈B的前3个元素不动，下标为【0，ltop】。

        其次考虑右边的情况，通过观察，发现index为5的元素对应到11，所以即为newLen-1，而先前的rtop从双端栈A的3变到了双端栈B的9，可以观察到9 = 12 - 3;此时rtop =  newLen -  size（1）

这时候原先双端栈A的右边完全到了双端栈B的左边，完成了对双端栈A的扩容问题。

关于栈的习题应用：

1.关于题解回文数；

        给定一个字符串，判断是否该字符串是否是回文字符串，即"aba" 则为一个满足回文的条件；

  1. public class JudgingPalindrome {
  2.     public static void main(String[] args) {
  3.         solution01();
  4.         System.out.println(solution02());
  5.     }
  6.     //通过栈的思想
  7.     private static void solution01() {
  8.         String text = "上海自来水来自海上"; 
  9.         ArrayStack<Character> stack = new ArrayStack<>();
  10.            //遍历栈中元素
  11.          for (int i = 0; i < text.length(); i++) {
  12.             //对于栈中元素是奇是偶进行判断
  13.             if (text.length() % 2 == 1 && i == text.length() / 2) {
  14.                 continue;
  15.             }
  16.             char c = text.charAt(i);
  17.             //栈空进栈，相同时候元素弹出，不同时候进栈，判断最后是否栈为空，为空则回文
  18.             if (stack.isEmpty()) {
  19.                stack.push(c);
  20.             } else {
  21.                 if (c != stack.peek()) {
  22.                     stack.push(c);
  23.                 } else {
  24.                     stack.pop();
  25.                 }
  26.             }
  27.         }
  28.         System.out.println(stack.isEmpty());
  29.     }
  30.         //通过双指针的思想
  31.         private static boolean solution02() {
  32.         String text = "上海自来水来自海上";
  33.         //头指针
  34.         int i = 0;
  35.         //尾指针
  36.         int j = text.length() - 1;
  37.         //循环条件，头尾同时进行，首位匹配下一位，不同则返回false；
  38.         while (true) {
  39.             if (text.charAt(i) == text.charAt(j)) {
  40.                 i++;
  41.                 j--;
  42.             } else {
  43.                 return false;
  44.             }
  45.             //尾指针要小于等于头指针
  46.             if (j <= i) {
  47.                 return true;
  48.             }
  49.         }
  50.     }
  51. }

2.关于括号匹配问题

        给定一些列括号‘（‘ ，’）’，‘【‘，’】’等，判断给定的括号串，是否完全匹配。如：“（{（）（）}）”；

  1.  
  2. //括号匹配
  3. import java.util.HashMap;
  4.  
  5. public class MatchBracket {
  6.     public static void main(String[] args) {
  7.         solution01();
  8.         solution02();
  9.     }
  10.  
  11.     //通过栈的思想解决
  12.     private static void solution01() {
  13.         String str = "{()[[()]]<>{}()<>}()";
  14.         ArrayStack<Character> stack = new ArrayStack<>();
  15.      
  16.            //循环该数组下标，栈为空进栈
  17.             for (int i = 0; i < str.length(); i++) {
  18.             char c = str.charAt(i);
  19.             if (stack.isEmpty()) {
  20.                 stack.push(c);
  21.             } else {
  22.                //当前栈顶
  23.                 char top = stack.peek();
  24.                 //通过ascll码匹配当满足条件时候，弹栈，即完成匹配
  25.                 if (top - c == -1 || top - c == -2) {
  26.                     stack.pop();
  27.                 } else {
  28.                     stack.push(c);
  29.                 }
  30.             }
  31.         }
  32.         //当stack为空时候说明括号完全匹配
  33.         System.out.println(stack.isEmpty());
  34.     }
  35.         
  36.         //通过HashMap实现
  37.         private static void solution02() {
  38.         String str = "{()[[()]]<{()>}()";
  39.         //给定hashmap的键值对应关系
  40.         HashMap<Character,Character> map = new HashMap<>();
  41.         map.put('[',']');
  42.         map.put('<','>');
  43.         map.put('(',')');
  44.         map.put('{','}');
  45.         ArrayStack<Character> stack = new ArrayStack<>();
  46.         //遍历和法1相同
  47.         for (int i = 0; i < str.length(); i++) {
  48.             char c = str.charAt(i);
  49.             if (stack.isEmpty()) {
  50.                 stack.push(c);
  51.             } else {
  52.                 char top = stack.peek();
  53.                 //contains保证键值关系，包含时候，看c是否满足关系，满足时候弹栈，不满足继续入栈
  54.                 if (map.containsKey(top) && c == map.get(']')) {
  55.                     stack.pop();
  56.                 } else {
  57.                     stack.push(c);
  58.                 }
  59.             }
  60.         }
  61.         System.out.println(stack.isEmpty());
  62.     }
  63. }

3.简单计算器的实现

        给定（），+ - */四则运算，做出来一个简单的计算器 如(10+20/2*3)/2+8 = 28

        3.1中缀表达式计算器

  1. //中缀表达式计算器
  2. public class InfixCalculator {
  3.     public static void main(String[] args) {
  4.         String expression = "(10+20/2*3)/2+8";
  5.         try {
  6.             int result = evaluateExpression(expression);
  7.             System.out.println(result);
  8.         } catch (Exception e) {
  9.             e.printStackTrace();
  10.             System.out.println("Wrong expression :" + expression);
  11.         }
  12.     }
  13.  
  14.     private static int evaluateExpression(String expression) {
  15.         //需要两个辅助栈
  16.         ArrayStack<Character> operatorStack = new ArrayStack<>();
  17.         ArrayStack<Integer> numberStack = new ArrayStack<>();
  18.  
  19.         //格式化表达式
  20.         expression = insertBlanks(expression);
  21.         String[] tokens = expression.split(" ");
  22.         for (String token : tokens) {   //token == tokens[i]
  23.             //过滤空串
  24.             if (token.length() == 0) {
  25.                 continue;
  26.                 //遍历到 + - 号
  27.             } else if (token.equals("+") || token.equals("-")) {
  28.                 while (!operatorStack.isEmpty() && (operatorStack.peek() == '+' || operatorStack.peek() == '-' || operatorStack.peek() == '*' || operatorStack.peek() == '/')) {
  29.                     //如果之前是别的+ - * / 则需要弹栈 并计算
  30.                     processAnOperator(numberStack, operatorStack);
  31.                 }
  32.                 //如果操作符栈为空 或者 不为空但栈顶为(
  33.                 operatorStack.push(token.charAt(0));
  34.  
  35.                 //遍历到 * / 号
  36.             } else if (token.equals("*") || token.equals("/")) {
  37.                 while (!operatorStack.isEmpty() && (operatorStack.peek() == '*' || operatorStack.peek() == '/')) {
  38.                     //如果之前是别的* / 则需要弹栈 并计算
  39.                     processAnOperator(numberStack, operatorStack);
  40.                 }
  41.                 //如果操作符栈为空 或者 不为空但栈顶为(
  42.                 operatorStack.push(token.charAt(0));
  43.  
  44.                 //遍历到 (
  45.             } else if (token.equals("(")) {
  46.                 operatorStack.push(token.charAt(0));
  47.  
  48.                 //遍历到 )
  49.             } else if (token.equals(")")) {
  50.                 //只要操作符栈的栈顶不是左括号( 就挨个弹栈计算即可
  51.                 while (operatorStack.peek() != '(') {
  52.                     processAnOperator(numberStack, operatorStack);
  53.                 }
  54.                 //最后 清掉左括号
  55.                 operatorStack.pop();
  56.  
  57.                 //遍历到数字
  58.             } else {
  59.                 numberStack.push(new Integer(token));
  60.             }
  61.         }
  62.  
  63.         //处理最后面的操作符
  64.         while (!operatorStack.isEmpty()) {
  65.             processAnOperator(numberStack, operatorStack);
  66.         }
  67.         return numberStack.pop();
  68.     }
  69.  
  70.     //操作符栈弹栈一个元素 数字栈弹栈两个数字 进行计算 并将新的结果进栈到数字栈
  71.     private static void processAnOperator(ArrayStack<Integer> numberStack, ArrayStack<Character> operatorStack) {
  72.         char op = operatorStack.pop();
  73.         int num1 = numberStack.pop();
  74.         int num2 = numberStack.pop();
  75.         //num2 op num1
  76.         if (op == '+') {
  77.             numberStack.push(num2 + num1);
  78.         } else if (op == '-') {
  79.             numberStack.push(num2 - num1);
  80.         } else if (op == '*') {
  81.             numberStack.push(num2 * num1);
  82.         } else {
  83.             numberStack.push(num2 / num1);
  84.         }
  85.     }
  86.  
  87.     //对原表达式进行格式化处理 给所有的非数字字符两边添加空格
  88.     private static String insertBlanks(String expression) {
  89.         StringBuilder sb = new StringBuilder();
  90.         for (int i = 0; i < expression.length(); i++) {
  91.             char c = expression.charAt(i);
  92.             if (c == '(' || c == ')' || c == '+' || c == '-' || c == '*' || c == '/') {
  93.                 sb.append(' ');
  94.                 sb.append(c);
  95.                 sb.append(' ');
  96.             } else {
  97.                 sb.append(c);
  98.             }
  99.         }
  100.         return sb.toString();
  101.     }
  102. }

        3.2后缀表达式计算器

        

  1. //后缀表达式的计算器
  2. public class SuffixCalculator {
  3.     public static void main(String[] args) {
  4.         String infixExpression = "(10+20/2*3)/2+8";
  5.         String suffixExpression = InfixToSuffix.infixToSuffix(infixExpression);
  6.         int result = evaluateSuffix(suffixExpression);
  7.         System.out.println(result);
  8.     }
  9.  
  10.     private static int evaluateSuffix(String expression) {
  11.         ArrayStack<Integer> stack = new ArrayStack<>();
  12.         String[] tokens = expression.split(" ");
  13.         for (String token : tokens) {
  14.             if (token.length() == 0) {
  15.                 continue;
  16.             }
  17.             if (isNumber(token)) {
  18.                 stack.push(new Integer(token));
  19.             } else {
  20.                 processAnOperator(stack,token);
  21.             }
  22.         }
  23.         return stack.pop();
  24.     }
  25.  
  26.     private static void processAnOperator(ArrayStack<Integer> stack, String token) {
  27.         int num1 = stack.pop();
  28.         int num2 = stack.pop();
  29.         if (token.equals("+")) {
  30.             stack.push(num2 + num1);
  31.         } else if (token.equals("-")) {
  32.             stack.push(num2 - num1);
  33.         } else if (token.equals("*")) {
  34.             stack.push(num2 * num1);
  35.         } else if (token.equals("/")) {
  36.             stack.push(num2 / num1);
  37.         }
  38.     }
  39.  
  40.     private static boolean isNumber(String token) {
  41.         return token.matches("\\d+");
  42.     }
  43. }

        3.3中缀转换后缀

        

  1. //中缀表达式转后缀表达式
  2. public class InfixToSuffix {
  3.     public static void main(String[] args) {
  4.         String expression = "(10+20/2*3)/2+8";
  5.         expression = infixToSuffix(expression);
  6.         System.out.println(expression);
  7.     }
  8.     private static String infixToSuffix(String expression) {
  9.         //操作符的栈
  10.         ArrayStack<String> opStack = new ArrayStack<>();
  11.         //后缀表达式的线性表
  12.         ArrayList<String> suffixList = new ArrayList<>();
  13.         //格式化表达式
  14.         expression = insertBlanks(expression);
  15.         String[] tokens = expression.split(" ");
  16.         for (String token : tokens) {
  17.             //过滤空串
  18.             if (token.length() == 0) {
  19.                 continue;
  20.             }
  21.             //判断操作符+ - * /
  22.             if (isOperator(token)) {
  23.                 /*
  24.                 什么时候操作符进栈？
  25.                 1.如果栈为空
  26.                 2.如果栈顶是 (
  27.                 3.如果栈顶是操作符，且优先级比当前token小
  28.                 什么时候需要将栈顶操作符出栈？
  29.                 1.栈顶操作符的优先级 >= 当前token
  30.                 */
  31.                 while (true) {
  32.                     if (opStack.isEmpty() || opStack.peek().equals("(") || priority(opStack.peek()) < priority(token)) {
  33.                         opStack.push(token);
  34.                         break;
  35.                     }
  36.                     suffixList.add(opStack.pop());
  37.                 }
  38.             } else if (token.equals("(")) {
  39.                 opStack.push(token);
  40.             } else if (token.equals(")")) {
  41.                 while (!opStack.peek().equals("(")) {
  42.                     suffixList.add(opStack.pop());
  43.                 }
  44.                 opStack.pop();
  45.             } else if (isNumber(token)) {
  46.                 suffixList.add(token);
  47.             } else {
  48.                 throw new IllegalArgumentException("wrong char :" + expression);
  49.             }
  50.         }
  51.         while (!opStack.isEmpty()) {
  52.             suffixList.add(opStack.pop());
  53.         }
  54.         //将数字元素和操作符元素进行拼接
  55.         StringBuilder sb = new StringBuilder();
  56.         for (int i = 0; i < suffixList.size(); i++) {
  57.             sb.append(suffixList.get(i));
  58.             sb.append(' ');
  59.         }
  60.         return sb.toString();
  61.     }
  62.  
  63.     private static int priority(String token) {
  64.         if (token.equals("+") || token.equals("-")) {
  65.             return 0;
  66.         }
  67.         if (token.equals("*") || token.equals("/")) {
  68.             return 1;
  69.         }
  70.         return -1;
  71.     }
  72.  
  73.     private static boolean isNumber(String token) {
  74.         return token.matches("\\d+");
  75.     }
  76.  
  77.     private static boolean isOperator(String token) {
  78.         return token.equals("+") || token.equals("-") || token.equals("*") || token.equals("/");
  79.     }
  80.  
  81.     //对原表达式进行格式化处理 给所有的非数字字符两边添加空格
  82.     private static String insertBlanks(String expression) {
  83.         StringBuilder sb = new StringBuilder();
  84.         for (int i = 0; i < expression.length(); i++) {
  85.             char c = expression.charAt(i);
  86.             if (c == '(' || c == ')' || c == '+' || c == '-' || c == '*' || c == '/') {
  87.                 sb.append(' ');
  88.                 sb.append(c);
  89.                 sb.append(' ');
  90.             } else {
  91.                 sb.append(c);
  92.             }
  93.         }
  94.         return sb.toString();
  95.     }
  96. }

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/611819
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号