Submit: 3458 Solved: 1158
Description
有一天,由于某种穿越现象作用,你来到了传说中的小人国。小人国的布局非常奇特,整个国家的交通系统可
以被看成是一个2行C列的矩形网格,网格上的每个点代表一个城市,相邻的城市之间有一条道路,所以总共有2C个
城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞,两座城市之间的道路会变得不连通,
直到拥堵解决,道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事,部长听说你来自一个科技高度
发达的世界,喜出望外地要求你编写一个查询应答系统,以挽救已经病入膏肓的小人国交通系统。 小人国的交通
部将提供一些交通信息给你,你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式:
Close r1 c1 r2 c2:相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了;Open r1 c1 r2 c2:相邻的两座城
市(r1,c1)和(r2,c2)之间的道路被疏通了;Ask r1 c1 r2 c2:询问城市(r1,c1)和(r2,c2)是否连通。如果存在一
条路径使得这两条城市连通,则返回Y,否则返回N;
Input
第一行只有一个整数C,表示网格的列数。接下来若干行,每行为一条交通信息,以单独的一行“Exit”作为
结束。我们假设在一开始所有的道路都是堵塞的。我们保证 C小于等于100000,信息条数小于等于100000。
Output
对于每个查询,输出一个“Y”或“N”。
Sample Input
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit
Sample Output
N
HINT
Source
线段树 脑洞题
学自http://blog.csdn.net/huanghongxun/article/details/51213009
exm?线段树怎么还能这么玩儿啊?
矩形只有两行,显然(根本不)可以想到把两行并到一起处理。
对于一个矩形,我们记录它左上角、左下角、右上角、右下角四个方块之间的连通情况,共有6种。
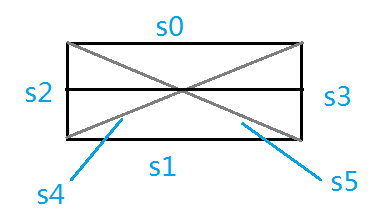
如上图: S0:上方连通 S1:下方连通 S2:左上和左下连通 S3:右上和右下连通 S4:左下和右上连通 S5:左上和右下连通
在所维护矩形只有一列的时候,只剩下两种情况:上下不连通(只有s0和s1为true),上下连通(全为true)
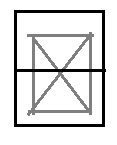
在改变某一列连通状态时,我们从左区间提取出它最右面的一列,利用该列和左右区间的所有s信息就可以算出大区间的s信息。
用线段树可以方便地维护

在改变同一行的相邻两列的连通状态时,也可以类似地维护
查询两格(x1,y1) (x2,y2)是否联通的时候,由于可能会存在“先往反方向走出[y1,y2]区间,再绕回来,使得两点联通”这种情况,所以不能只查[y1,y2]区间,而要查询[1,y1],[y1,y2],[y2,m]三段区间来判断答案。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 using namespace std; 6 const int mxn=100010; 7 int read(){ 8 int x=0,f=1;char ch=getchar(); 9 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 10 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 11 return x*f; 12 } 13 struct node{ 14 int s[6]; 15 }t[mxn<<2],bas[2]; 16 int id[2][mxn],ict; 17 int mp[mxn]; 18 #define ls rt<<1 19 #define rs rt<<1|1 20 inline node merge(const node &a,const node &b,int mid){ 21 node ans; 22 int x=mp[id[0][mid]],y=mp[id[1][mid]]; 23 ans.s[0]=(a.s[0]&x&b.s[0])|(a.s[4]&y&b.s[5]); 24 ans.s[1]=(a.s[1]&y&b.s[1])|(a.s[5]&x&b.s[4]); 25 ans.s[2]= a.s[2] |(a.s[0]&x&b.s[2]&y&a.s[1]); 26 ans.s[3]= b.s[3] |(b.s[0]&x&a.s[3]&y&b.s[1]); 27 ans.s[4]=(a.s[4]&y&b.s[1])|(a.s[0]&x&b.s[4]); 28 ans.s[5]=(a.s[1]&y&b.s[5])|(a.s[5]&x&b.s[0]); 29 return ans; 30 } 31 void Build(int l,int r,int rt){ 32 if(l==r){t[rt]=bas[0];return;} 33 int mid=(l+r)>>1; 34 Build(l,mid,ls);Build(mid+1,r,rs); 35 return; 36 } 37 void update(int x1,int x2,int y1,int y2,int v,int l,int r,int rt){ 38 if(l==r && x1!=x2 && y1==y2){ 39 t[rt]=bas[v];//该列上下联通 40 return; 41 } 42 int mid=(l+r)>>1; 43 if(x1==x2 && y1==mid){ 44 mp[id[x1][y1]]=v; 45 t[rt]=merge(t[ls],t[rs],mid); 46 return; 47 } 48 // 49 if(y1<=mid) 50 update(x1,x2,y1,y2,v,l,mid,ls); 51 else update(x1,x2,y1,y2,v,mid+1,r,rs); 52 t[rt]=merge(t[ls],t[rs],mid); 53 return; 54 } 55 node query(int L,int R,int l,int r,int rt){ 56 if(L<=l && r<=R)return t[rt]; 57 int mid=(l+r)>>1; 58 if(R<=mid)return query(L,R,l,mid,ls); 59 else if(L>mid)return query(L,R,mid+1,r,rs); 60 else return merge(query(L,mid,l,mid,ls),query(mid+1,R,mid+1,r,rs),mid); 61 } 62 int m; 63 int ask(int x1,int y1,int x2,int y2){ 64 node L=query(1,y1,1,m,1); 65 node R=query(y2,m,1,m,1); 66 node M=query(y1,y2,1,m,1); 67 if(x1==x2){ 68 return M.s[x1] || ( (!x1) && ((L.s[3]&M.s[5]) || (M.s[4]&R.s[2])) ) || 69 ( (x1) && ( (L.s[3]&M.s[4]) || (M.s[5]&R.s[2]) )) || 70 (M.s[!x1]&L.s[3]&R.s[2]); 71 } 72 else if((!x1) && x2){ 73 return M.s[4] | (L.s[3]&M.s[1]) | (M.s[0]&R.s[2]) | (L.s[3]&R.s[2]&M.s[5]); 74 } 75 else{ 76 return M.s[5] | (L.s[3]&M.s[0]) | (M.s[1]&R.s[2]) | (L.s[3]&R.s[2]&M.s[4]); 77 } 78 } 79 #undef ls 80 #undef rs 81 int main(){ 82 int i,j; 83 m=read(); 84 for(i=0;i<=1;i++) 85 for(j=1;j<=m;j++) 86 id[i][j]=++ict; 87 // 88 bas[0]=(node){1,1,0,0,0,0}; 89 bas[1]=(node){1,1,1,1,1,1}; 90 Build(1,m,1); 91 char op[5]; 92 int x1,y1,x2,y2; 93 while(1){ 94 scanf("%s",op); 95 if(op[0]=='E')break; 96 x1=read();y1=read();x2=read();y2=read(); 97 --x1;--x2;// 98 if(y1>y2)swap(x1,x2),swap(y1,y2); 99 switch(op[0]){ 100 case 'C':{ 101 update(x1,x2,y1,y2,0,1,m,1); 102 break; 103 } 104 case 'O':{ 105 update(x1,x2,y1,y2,1,1,m,1); 106 break; 107 } 108 case 'A':{ 109 int ans=ask(x1,y1,x2,y2); 110 ans?puts("Y"):puts("N"); 111 break; 112 } 113 } 114 } 115 return 0; 116 }


