数据结构与算法：时间复杂度与空间复杂度_大o渐进法 只保留最高项

目录

算法复杂度

时间复杂度

定义       

大O渐进法

大O推导方法

常见举例

计算时间复杂度

1.常数阶O(1)

2.线性阶O(n)

3.平方阶O(n²)

4.对数阶O(log n)

5.线性对数阶O(nlog n)

6.立方阶O(n³)

空间复杂度

定义

空间复杂度计算

常见情形

1.常量空间

2.线性空间

3.二维空间

4.递归空间

时间与空间的取舍

---

算法复杂度

时间复杂度和空间复杂度合称为算法的复杂度；

时间复杂度：执行算法所需要的计算工作量

空间复杂度：对一个算法在运行过程中临时占用存储空间大小的量度

        算法的复杂性体运行该算法时的计算机所需资源的多少上，计算机资源最重要的是时间和空间（即寄存器）资源，因此复杂度分为时间和空间复杂度。

时间复杂度

定义       

        一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度，记为T(n)。

        一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f (n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记T(n)=O(f(n))，称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度

时间复杂度是对算法本身效率的度量，它与运行环境、硬件和软件平台无关。

大O渐进法

用于表示时间复杂度和空间复杂度的一个工具、一种形式。用O( )来体现算法时间复杂度的记法；大O表示法所表示的是一个算法在最糟糕情况下的运行时间

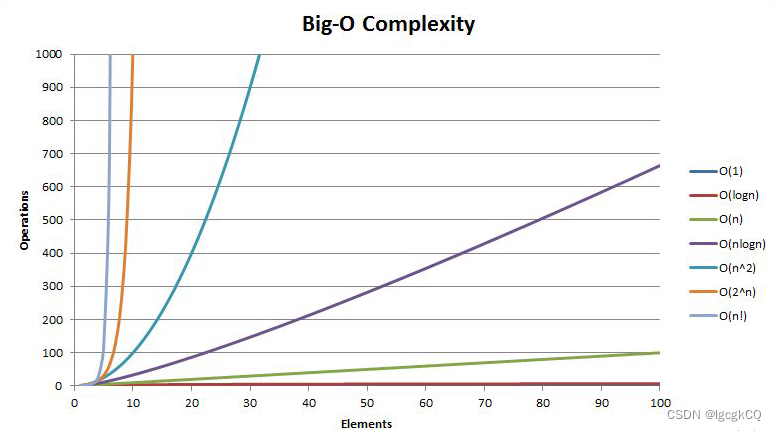
大O推导方法

1.用常数1来取代运行时间中所有加法常数。

2.修改后的运行次数函数中，只保留最高阶项

3.最高项除去其相乘的常数，得到的结果就是大O阶

常见举例

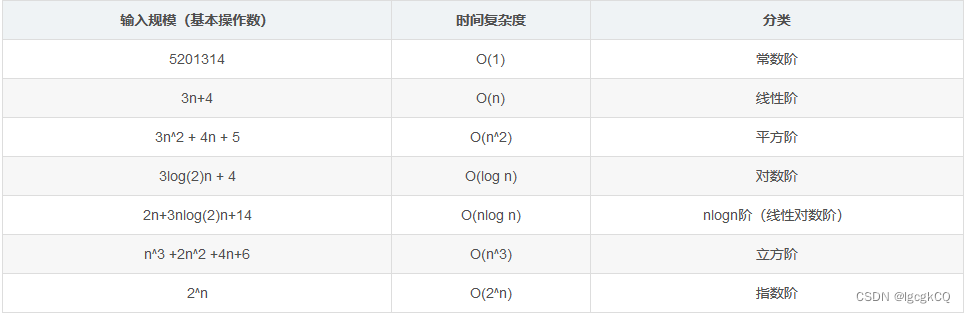
常见的时间复杂度所消耗的时间从小到大依次是：

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

计算时间复杂度

计算时间复杂度主要看执行的次数和输入的关系

1.常数阶O(1)

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)

int i = 1;

int j = 2;

int n = i + j;

2.线性阶O(n)

for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度

for(int i=0;i<=n;i++){

        j = i;

        j++;

}

3.平方阶O(n²)

如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²) 了

for(x = 1;i<=n;x++){

        for(int i=0;i<=n;i++){

                j = i;

                j++;

        }

}

4.对数阶O(log n)

int i = 1;

while(i < n){

        i = i * 2;

}

假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2^n

5.线性对数阶O(nlog n)

将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)

for(m=1; m<n; m++){
    i = 1;
    while(i<n){
        i = i * 2;
    }
}

6.立方阶O(n³)

参考O(n²) ，O(n³)相当于三层n循环，其它的类似

空间复杂度

定义

一个程序的空间复杂度是指运行完一个程序所需内存的大小，利用程序的空间复杂度，可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分：

(1):固定部分：这部分空间的大小与输入/输出的数据的个数多少、数值无关，主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间，这部分属于静态空间。

(2):可变空间：这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等，这部分的空间大小与算法有关。一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))，其中n为问题的规模，S(n)表示空间复杂度

只要算法不涉及到动态分配的空间以及递归、栈所需的空间，空间复杂度通常为0(1)

空间复杂度计算

常见情形

1.常量空间

当算法的存储空间大小固定，和输入规模没有直接的关系时，空间复杂度记作O(1)

void fun1(int n){

        int var = 3;

        ......

}

2.线性空间

当算法分配的空间是一个线性的集合（如数组），并且集合大小和输入规模n成正比时，空间复杂度记作O(n)

void fun2(int n){

        int[] var = new int[n];

        ......

}

3.二维空间

当算法分配的空间是一个二维数组集合，并且集合的长度和宽度都与输入规模n成正比时，空间复杂度记作O(n^2)

void fun3(int n){

        int[][] var = new int[n][n];

        ......

}

4.递归空间

        递归是一个比较特殊的场景。虽然递归代码中并没有显式地声明变量或集合，但是计算机在执行程序时，会专门分配一块内存，用来存储“方法调用栈”;“方法调用栈”包括进栈和出栈两个行为。

        当进入一个新方法时，执行入栈操作，把调用的方法和参数信息压入栈中。
        当方法返回时，执行出栈操作，把调用的方法和参数信息从栈中弹出

void fun4(int n){

        if(n<=1){

                return;

        }

        fun4(n-1);

}

递归的深度是n，那么空间复杂度就是O(n)

时间与空间的取舍

        对于算法的性能，需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性，即时间和空间复杂度皆较低。而实际上，对于某个算法问题，同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度，往往是以提升空间复杂度为代价的，反之亦然。

        人们之所以花大力气去评估算法的时间复杂度和空间复杂度，其根本原因是计算机的运算速度和空间资源是有限的，通常情况下，算法设计中一般会采取「空间换时间」的做法，即牺牲部分计算机存储空间，来提升算法的运行速度。