当前位置: article > 正文

最小堆&最大堆_legend_最小堆是递增

作者：笔触狂放9 | 2024-06-18 07:22:25

踩

最小堆是递增

最小堆：
（一）定义：
有一个关键码的结合K={k1,k2,k3,..kn},把它的所有的元素按照完全二叉树的顺序存储方式存放在一个数组中，其满足ki<=k(2*i+1)且ki<=k(2*i+2),(i=0,1,2...n/2-1),则这个集合为最小堆。

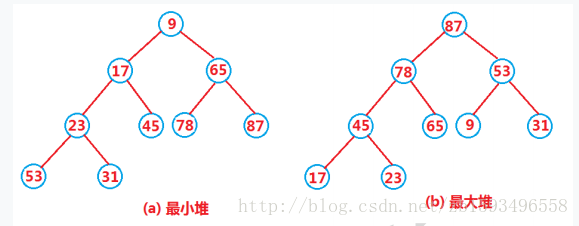
堆的存储可以看成是数组存储的变形，不过，堆的存储又具有二叉树的结构，堆的存储按类型可以分为大堆和小堆。小堆（大堆）中：任一节点的关键码均小于（大于）等于它的左右孩子的关键码，位于堆顶节点的关键码最小（最大），从根节点到每个结点的路径上数组元素组成的序列都是递增（递减）的。
大小堆的结构表示

（二）特点：

（1）最小堆为完全二叉树（所谓完全二叉树就是除了最后一层外，其他层的节点的个数必须是最大值，且最后一层的节点都必须集中在左侧.即最后一层从左往右数节点必须是紧挨着的，不能是中间空出一个，右边还有兄弟节点.）；

（2）顺序存储（即使用数组来表示完全二叉树）；
注：完全二叉树满足n0=n2+1(n0为度数为0的节点个数，n2为度数为2的节点个数)
n=n0+n2=n2+1+n2; 所以n2=(n-1)/2;
n2=(n-1)/2；所以双分支节点的下标范围为：0~n/2-1
叶子节点的下标范围为：n/2~n-1;

（3）最小堆需要对于任何一个父节点而言，左右孩子的节点值必须大于或等于自身的值；

（三）最小堆的存储结构：

（1）最小堆存储在下标从0开始的一位数组里；
（2）对于下标为i的节点：
1.若i=0,则节点i为根节点，无父节点，否则父节点为(i-1)/2;
2.若2*i+1>n-1;则节点i无左孩子，否则左孩子为2*i+1;
3.若2*i+2>n-2;则节点i无右孩子，否则右孩子为2*i+2;

（3）最小堆的类型定义：
typedef struct MinHeap{
DataType heap[Maxsize];
int currentSize;//小根堆中当前的元素个数
};

（四）最小堆节点的插入：
（1）最小堆为完全二叉树，新插入的节点都是作为叶子节点的。
（2）思想：
新插入的节点都是叶子节点，从下往上与其父节点比较，调整。

（3）代码实现：
/*
注：minheap为引用型参数。
*/
int insert(MinHeap & minheap, DataType x){
if(minheap.currentSize==Maxsize) return 0;//堆满
minheap.heap[currentSize]=x;

//已经使用的位置为：0~（currentSize-1）；将新节点插入到最后的位置。
siftup(minheap,minheap.currentSize);//从下到上调整
minheap.currentSize++;
return 1;
}

/*
目的：从下标为start的叶子节点开始，从下往上一直调整.
如果子女的值小于父节点的值，则交换。
siftUp的时间复杂度为：O(logn)

注：siftup 的名称一般也有叫 pushHeap的；
*/
void siftup(MinHeap & minheap,int start){
DataType datatemp=minheap.heap[start];
//临时变量保存start处节点值，同时也相当于start处挖了一个坑，可以来填数。
int current_index=start;
int father_index=(current_index-1)/2;

while(current_index>0){
  if(minheap.heap[father_index]<=datatemp) break;
  else {
  minheap.heap[current_index]=minheap.heap[father_index];
  //填数，将父节点下调下来，则在原父节点位置留下了一个坑。
  current_index=father_index;
  //current_index保留的是父节点位置，即空缺需要填数的位置。
  father_index=(current_index-1)/2;
  }
}
minheap.heap[current_index]=datatemp;//
}

（五）节点的删除：
（1）最小堆元素的删除是删除堆顶的元素，（即堆中最小值）；
保存堆顶，然后将最尾端的节点值放在堆顶，然后siftdown调整即可。

（2）代码实现：
/*
删除成功，则返回1，否则返回0.
注：minheap,x均为引用型参数。
siftDown时间复杂度为:O(lgn)
*/
int romoveMin(MinHeap & minheap, DataType & x){
if(0==minheap.currentSize) return 0;
x=minheap.heap[0];
minheap.heap[0]=minheap.heap[minheap.currentSize-1];//将堆尾节点值放入堆头。
minheap.currentSize--;
siftDown(minheap,0,minheap.currentSize-1);
return 1;
}

/*
目的：
siftDown是一个从上往下的刷选方法。从非叶子节点i开始向下调整，前提是它的两棵子树都已经是堆。
，从节点i开始到lastIndex为止，从上而下比较。

注：siftdown一般也叫 popHeap;
*/

void siftDown(MinHeap & minheap, int i, int lastIndex){
int current=i;//标识当前节点
int minSon=2*current+1;//minSon为左右孩子中，值更小的一个孩子的下标。
DataType datatemp=minheap.heap[i];
//临时变量保存i处节点值，同时在i处挖了一个坑，可以填数。
while(current<=lastIndex){
if(minheap.heap[minSon]>minheap.heap[minSon+1])
minSon++;//取左右孩子中较小的一个的下标

  if(minheap.heap[minSon]<tempdata){//孩子节点与保存值比较
   minheap.heap[current]=minheap.heap[minSon];
   //current处填数，同时在原minSon处形成一个坑。
   current=minSon;//在current处有一个坑
   minSon=2*current+1;
  }
  else break;
}

minheap.heap[current]=datatemp;

}

（六）最小堆的构建：
（1）方法一：不断的插入节点；
（2）方法二：筛选法建立：
/*
思想：
1.在堆中的叶子节点的编号是从n/2~n-1，并且叶子节点可以看出是子堆。
2.非叶子节点的编号为0~n/2-1，叶子节点已经是堆，所以只需要对从下而上的每一个非叶子节点进行自上而下的调整。
注：minheap为引用型参数。
*/

void createMinHeap(Minheap & minheap, DataType [] arr, int n){
for(int i=0;i<n;i++)//堆中的数组初始化
minheap.heap[i]=arr[i];

minheap.currentSize=n;
int curPos=(n/2)-1;

while(curPos>=0){
siftDown(minheap,curPos,minheap.currentSize-1);
curPos--;
}

}

-------------------------

最大堆的范例：

（1）插入元素：

现在假设你有这样子的一个堆