devbox
笔触狂放9
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

典型题（相关知识点：字符串，二分，高精度，线性筛，排序）_f(n) % n == 0?

作者：笔触狂放9 | 2024-02-10 19:05:50

赞

踩

f(n) % n == 0?

1 - 排序 —— HDU - 1106

输入一行数字，如果我们把这行数字中的‘5’都看成空格，那么就得到一行用空格分割的若干非负整数（可能有些整数以‘0’开头，这些头部的‘0’应该被忽略掉，除非这个整数就是由若干个‘0’组成的，这时这个整数就是0）。

你的任务是：对这些分割得到的整数，依从小到大的顺序排序输出。

Input

输入包含多组测试用例，每组输入数据只有一行数字（数字之间没有空格），这行数字的长度不大于1000。

输入数据保证：分割得到的非负整数不会大于100000000；输入数据不可能全由‘5’组成。

Output

对于每个测试用例，输出分割得到的整数排序的结果，相邻的两个整数之间用一个空格分开，每组输出占一行。

Sample Input

0051231232050775

Sample Output

0 77 12312320

#include <iostream>
#include <cstdio> 
#include <algorithm> 
using namespace std;
 
#define MAXN 1000005 
char str[MAXN]; 
int arr[MAXN];
void output(int n) {    
	for (int i = 0; i < n; i++) {        
		if (i) cout << " ";        
		cout << arr[i];    
	}    
	cout << endl;    
	return ; 
}
 
int main() {    
	while (scanf("%s", str) != EOF) {        
		int cnt = 0, num = -1; // 因为分割后的数字为非负数所以 num 赋值为 -1        
		for (int i = 0; str[i]; i++) {            
			if (str[i] == '5') {                
				if (num == -1) continue;                
				arr[cnt++] = num;                
				num = -1; // 获取到一个完整的数字后把 num 赋为 -1                
				continue;            
			}            
			if (num == -1) num = str[i] - 48;            
			else num = num * 10 + (str[i] - 48);        
		}        
		if (num != -1) arr[cnt++] = num;        
		sort(arr, arr + cnt);        
		output(cnt);    
	}    
	return 0; 
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37

2 - 高精度

Fibonacci数列，定义如下：
f(1)=f(2)=1
f(n)=f(n-1)+f(n-2) n>=3。
计算第n项Fibonacci数值。

Input

输入第一行为一个整数N，接下来N行为整数Pi（1<=Pi<=1000）。

Output

输出为N行，每行为对应的f(Pi)。

Sample Input

5
1
2
3
4
5

Sample Output

1
1
2
3
5

#include <iostream>
using namespace std;
#define MAXN 1005
int f[MAXN][MAXN] = {0};
// 打表、大数加法
void add() {
	for (int i = 3; i <= 1000; i++) {
		f[i][0] = f[i-1][0];
		for (int j = 1; j <= f[i-1][0]; j++) f[i][j] = f[i-1][j] + f[i-2][j];
		for (int j = 1; j <= f[i][0]; j++) {
			if (f[i][j] < 10) continue;
			f[i][j + 1] += f[i][j] / 10;
			f[i][j] %= 10;
			f[i][0] += (j == f[i][0]);
		}
	}
	return ;
}
void init() {
// 将前两项赋值为 1
	f[1][0] = f[1][1] = 1;
	f[2][0] = f[2][1] = 1;
	add();
	return ;
}
void output(int n) {
	for (int i = f[n][0]; i >= 1; i--) cout << f[n][i];
	cout << endl;
	return ;
}

int main() {
	init();
	int t, n;
	cin >> t;
	while (t--) {
		cin >> n;
		output(n);
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41

3 - 素数 HDU - 1262

哥德巴赫猜想大家都知道一点吧.我们现在不是想证明这个结论,而是想在程序语言内部能够表示的数集中,任意取出一个偶数,来寻找两个素数,使得其和等于该偶数.
做好了这件实事,就能说明这个猜想是成立的.
由于可以有不同的素数对来表示同一个偶数,所以专门要求所寻找的素数对是两个值最相近的.

Input

输入中是一些偶整数M(5<M<=10000).

Output

对于每个偶数,输出两个彼此最接近的素数,其和等于该偶数.

Sample Input

20 30 40

Sample Output

7 13
13 17
17 23

#include <iostream>
using namespace std;
#define MAXN 20000

int is_prime[MAXN], prime[MAXN];

void init_prime() {
	is_prime[0] = is_prime[1] = 1;
	for (int i = 2; i < MAXN; i++) {
		if (!is_prime[i]) prime[++prime[0]] = i;
		for (int j = 1; j <= prime[0] && i * prime[j] < MAXN; j++) {
			is_prime[i * prime[j]] = 1;
			if (i % prime[j] == 0) break;
		}
	}
	return ;
}
int main() {
	init_prime();
	int x;
	while (cin >> x) {
		for (int i = x / 2; i >= 2; i--) {
			if (!is_prime[i] && !is_prime[x - i]) {
				cout << i << " " << x - i << endl;
				break;
			}
		}
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30

4 - 字符串 HDU - 1020

Given a string containing only ‘A’ - ‘Z’, we could encode it using the following method:
1. Each sub-string containing k same characters should be encoded to “kX” where “X” is the only character in this sub-string.
2. If the length of the sub-string is 1, ‘1’ should be ignored.

Input

The first line contains an integer N (1 <= N <= 100) which indicates the number of test cases. The next N lines contain N strings. Each string consists of only ‘A’ - ‘Z’ and the length is less than 10000.

Output

For each test case, output the encoded string in a line.

Sample Input

2
ABC
ABBCCC

Sample Output

ABC
A2B3C

#include <iostream>
using namespace std;
#define MAXN 10005
int main() {
	int t;
	cin >> t;
	while (t--) {
		char str[MAXN] = {0};
		int cnt = 0; // 记录该字符的个数
		cin >> str;
		for (int i = 0; str[i]; i += cnt) {
			cnt = 1;
			while (str[i] == str[i + cnt]) ++cnt;
			if (cnt > 1) cout << cnt;
			cout << str[i];
		}
		cout << endl;
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20

5 - 数学 HDU - 1018

In many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number.

Input

Input consists of several lines of integer numbers. The first line contains an integer n, which is the number of cases to be tested, followed by n lines, one integer 1 ≤ n ≤ 10^7 on each line.

Output

The output contains the number of digits in the factorial of the integers appearing in the input.

Sample Input

2
10
20

Sample Output

7
19

思路解析

求一个数的位数可以用int(log10(n)) + 1 ，要求 n! 的位数可以用 int(log10(n!)) + 1 =>
int(log10(1) + log10(2) + … + log10(n)) + 1

#include <iostream>
#include <cmath>
using namespace std;
int main() {
	int t, n;
	cin >> t;
	while (t--) {
		cin >> n;
		double cnt = 0;
		for (int i = 1; i <= n; i++) {
			cnt += log10(i);
		}
		cout << int(cnt) + 1 << endl; // 此处如果用floor函数也需再转成int
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

6 - 贪心 HDU - 1789

Ignatius has just come back school from the 30th ACM/ICPC. Now he has a lot of homework to do. Every teacher gives him a deadline of handing in the homework. If Ignatius hands in the homework after the deadline, the teacher will reduce his score of the final test. And now we assume that doing everyone homework always takes one day. So Ignatius wants you to help him to arrange the order of doing homework to minimize the reduced score.

Input

The input contains several test cases. The first line of the input is a single integer T that is the number of test cases. T test cases follow.
Each test case start with a positive integer N(1<=N<=1000) which indicate the number of homework… Then 2 lines follow. The first line contains N integers that indicate the deadlines of the subjects, and the next line contains N integers that indicate the reduced scores.

Output

For each test case, you should output the smallest total reduced score, one line per test case.

Sample Input

3
3
3 3 3
10 5 1
3
1 3 1
6 2 3
7
1 4 6 4 2 4 3
3 2 1 7 6 5 4

Sample Output

0
3
5

题目大意

有 n 个任务，给出每个任务的截止时间和分数，如果不能在截止时间内完成，便扣除该任务的分数，求
最少扣除多少分。

思路解析

贪心问题

  1. 按照分数降序排序（当分数相等时截止时间早的放在前面）
  2. 定义一个标记数组，标记该分数可以在哪天完成（截止时间内）
  3. 判断条件：如果能在该天完成，标记数组记为1，反之加上应该扣除的分数
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define MAXN 1005
struct Array {
	int date;
	int value;
};
bool cmp(Array a, Array b) {
	if (a.value == b.value) return a.date < b.date;
	return a.value > b.value;
}
int main() {
	int t, n;
	scanf("%d", &t);
	while (t--) {
		Array arr[MAXN];
		int vis[MAXN] = {0}; // 用来标记当天是否有任务，0为没有
		scanf("%d", &n);
		for (int i = 0; i < n; i++) scanf("%d", &arr[i].date);
		for (int i = 0; i < n; i++) scanf("%d", &arr[i].value);
		sort(arr, arr + n, cmp);
		int sum = 0;
		for (int i = 0; i < n; i++) {
			int flag = 0;
			for (int j = arr[i].date; j >= 1; j--) { // 寻找可以在哪天完成该任务
				if (!vis[j]) {
					vis[j] = 1;
					flag = 1;
					break;
				}
			}
			if (!flag) sum += arr[i].value;
		}
		printf("%d\n", sum);
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39

7 - 二分 HDU - 6216

A cubic number is the result of using a whole number in a multiplication three times. For example, 3×3×3=27 so 27 is a cubic number. The first few cubic numbers are 1,8,27,64 and 125. Given an prime number p. Check that if p is a difference of two cubic numbers.

Input

The first of input contains an integer T (1≤T≤100) which is the total number of test cases.
For each test case, a line contains a prime number p (2≤p≤10^12).

Output

For each test case, output ‘YES’ if given p is a difference of two cubic numbers, or ‘NO’ if not.

Sample Input

10
2
3
5
7
11
13
17
19
23
29

Sample Output

NO
NO
NO
YES
NO
NO
NO
YES
NO
NO

思路解析

假设 p = a^3 - b^3
p = a^3 - b^3 = (a - b) * (a^2 + ab + b^2)
由于 p 是素数，a^2 + ab + b^2恒大于0，所以 a-b = 1;
即(a - b) * (a^2 + ab + b^2) = 3b^2 + 3b + 1 。

  1. 根据p = 3b^2 + 3b + 1 ，可以先将 p 进行打表
  2. 在 p 数组上进行二分查找
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
#define MAXN 1000005
LL arr[MAXN];
void init() {
	for (LL i = 1; i < MAXN; i++) {
		arr[i] = 3 * i * i + 3 * i + 1;
	}
	return ;
}
int search(LL x) {
	int l = 1, r = MAXN - 1, mid;
	while (l <= r) {
		mid = l + (r - l) / 2;
		if (arr[mid] == x) return 1;
		if (arr[mid] < x) l = mid + 1;
		else r = mid - 1;
	}
	return 0;
}
int main() {
	init();
	int t;
	LL x;
	scanf("%d", &t);
	while (t--) {
		scanf("%lld", &x);
		if (search(x)) printf("YES\n");
		else printf("NO\n");
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34

8.The area HDU - 1071

Ignatius bought a land last week, but he didn’t know the area of the land because the land is enclosed by a parabola and a straight line. The picture below shows the area. Now given all the intersectant points shows in the picture, can you tell Ignatius the area of the land?

Note: The point P1 in the picture is the vertex of the parabola.
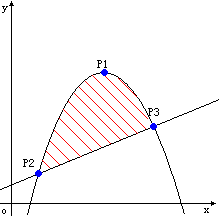
在这里插入图片描述

Input

The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each test case contains three intersectant points which shows in the picture, they are given in the order of P1, P2, P3. Each point is described by two floating-point numbers X and Y(0.0<=X,Y<=1000.0).

Output

For each test case, you should output the area of the land, the result should be rounded to 2 decimal places.

Sample Input

2
5.000000 5.000000
0.000000 0.000000
10.000000 0.000000
10.000000 10.000000
1.000000 1.000000
14.000000 8.222222

Sample Output

33.33
40.69

Hint

For float may be not accurate enough, please use double instead of float.

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iomanip>
using namespace std;
double a, b, c, d, k, x1, y1, x2, y2, x3, y3;
//y = a(x-b)^2+c
//y = kx+d;

double fun(int x) {
 //f = ax^2-(2ab+k)x+ab^2+c-d
	return (1 / 3.0) * a * x * x * x - (1 / 2.0) * (2 * a * b + k) * x * x + (a * b * b + c - d) * x; 
}

int  main() {
	int t;
	cin >> t;
	while (t--) {
		cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3;
		b = x1;
		c = y1;
		a = (y2 - y1) / ((x2 - x1) * (x2 - x1));
		k = (y3 - y2) / (x3 - x2);
		d = y2 - x2 * k;
		cout << fixed << setprecision(2) << fun(x3) - fun(x2) << endl;
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29

9 绝对值排序 HDU - 2020

输入n(n<=100)个整数，按照绝对值从大到小排序后输出。题目保证对于每一个测试实例，所有的数的绝对值都不相等。

Input

输入数据有多组，每组占一行，每行的第一个数字为n,接着是n个整数，n=0表示输入数据的结束，不做处理。

Output

对于每个测试实例，输出排序后的结果，两个数之间用一个空格隔开。每个测试实例占一行。

Sample Input

3 3 -4 2
4 0 1 2 -3
0

Sample Output

-4 3 2
-3 2 1 0

//选择排序
#include <iostream>
#include <cstdio>
using namespace std;
int main() {
	int ans[101];
	int n;
	while(cin >> n && n) {
		for(int i = 1; i <= n; ++i) {
			cin >> ans[i];
		}
		for(int i = 1; i < n; ++i) {
			int k = i;
			for(int j = i + 1; j <= n; ++j) {
				int a = abs(ans[j]), b = abs(ans[k]);
				if(a > b) k = j;
			}
			swap(ans[i], ans[k]);
		}
		cout << ans[1];
		for(int i = 2; i <= n; ++i)
			cout << " " << ans[i];
		cout << endl;
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/75145
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号