粒子群算法【python实现】_粒子集群算法python实现

概要

提示：这里可以添加技术概要

原理参考：
https://zhuanlan.zhihu.com/p/346355572
编程参考：
https://github.com/Tonghui-Wang/Adaptive_Admittance_Control
https://blog.csdn.net/xyisv/article/details/79058574

完整代码

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt


# ----------------------PSO参数设置---------------------------------
class PSO:
    def __init__(self, pN, dim, max_iter):
        self.wlimit = np.array([0.4, 2]) # w范围
        self.c1 = 2
        self.c2 = 2
        self.max_iter = max_iter  # 进化次数
        self.pN = pN  # 种群规模
        self.dim = dim  # 粒子维度,即目标函数的自变量个数
        self.cost = np.array([np.inf] * self.pN)  # 个体适应度代价
        self.pbest = np.zeros((self.pN, self.dim))  # 个体最值
        self.gbest = np.zeros((1, self.dim))  # 群体最值
        self.particle = np.zeros((self.pN, 2, self.dim))  # n个粒子，粒子每行分别表示位置、速度
        self.xlimit = np.array([[-5, -5], [5, 5]])  # 目标函数自变量的取值范围
        self.vmax = np.array([1, 1])  # 最大进化速度

    # ---------------------目标函数-----------------------------
    def function(self, x, y):
        return x * x + y * y - 25

    # ---------------------初始化种群----------------------------------
    def init_Population(self):
        for i in range(self.pN):
        		 # 位置初始化
            self.particle[i, 0, :] = np.random.rand(1, self.dim) * (
                    self.xlimit[1, :] - self.xlimit[0, :]) + self.xlimit[0, :]
             # 速度初始化
            self.particle[i, 1, :] = np.random.rand(1, self.dim) * self.vmax

    # ----------------------更新粒子位置----------------------------------

    def iterator(self):
        fitness = np.zeros((self.dim, self.max_iter)) # 保存每次迭代的种群最佳位置
        for t in range(self.max_iter):
            # 更新粒子群参数
            w = self.wlimit[1] - (self.wlimit[1] - self.wlimit[0]) * t / self.max_iter
            # 适应度评价
            for i in range(self.pN):  # 循环n个粒子
                error = np.absolute(self.function(self.particle[i, 0, 0], self.particle[i, 0, 1]))
                if error < self.cost[i]:  # 粒子当前代价小于粒子最小代价
                    self.cost[i] = error  # 更新粒子最小代价
                    self.pbest[i, :] = self.particle[i, 0, :]  # 更新粒子最优位置
                i = np.argmin(self.cost)  # 找到最小代价索引
                self.gbest = self.pbest[i, :]  # 将最小代价的个体最优位置赋值给群体最优位置
            fitness[0][t] = self.gbest[0]
            fitness[1][t] = self.gbest[1]
            # 更新粒子状态
            for i in range(self.pN):
                self.particle[i, 1, :] = w * self.particle[i, 1, :] + self.c1 * np.random.rand(self.dim) * \
                                         (self.pbest[i, :] - self.particle[i, 0, :]) + self.c2 * np.random.rand(
                    self.dim) * \
                                         (self.gbest[:] - self.particle[i, 0, :])  # 个体速度进化
                self.particle[i, 1, :] = np.minimum(self.particle[i, 1, :], self.vmax)  # 最大速度进化约束
                self.particle[i, 0, :] = self.particle[i, 0, :] + self.particle[i, 1, :]  # 个体位置进化
                self.particle[i, 0, :] = np.maximum(self.particle[i, 0, :], self.xlimit[0, :])  # 最小位置进化约束
                self.particle[i, 0, :] = np.minimum(self.particle[i, 0, :], self.xlimit[1, :])  # 最大位置进化约束
        return fitness

        # ----------------------程序执行-----------------------


my_pso = PSO(pN=30, dim=2, max_iter=100)
my_pso.init_Population()
fitness = my_pso.iterator()
print("x = ", fitness[0][99])
print("y = ", fitness[1][99])
# -------------------画图--------------------
plt.figure()
plt.subplot(2, 1, 1)
plt.title("Fitness over iterations")
plt.xlabel("Iterations")
plt.ylabel("x")
plt.plot(range(1, my_pso.max_iter + 1), fitness[0])
# plt.yticks(np.arange(min(fitness[0]), max(fitness[0]), step=1))  # 设置y轴刻度

plt.subplot(2, 1, 2)
plt.title("Fitness over iterations")
plt.xlabel("Iterations")
plt.ylabel("y")
plt.plot(range(1, my_pso.max_iter + 1), fitness[1])
# plt.yticks(np.arange(min(fitness[1]), max(fitness[1]), step=1))  # 设置y轴刻度

plt.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

提示：这里可以添加技术整体架构

运行结果

提示：这里可以添加技术名词解释

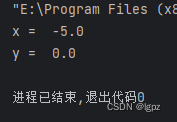
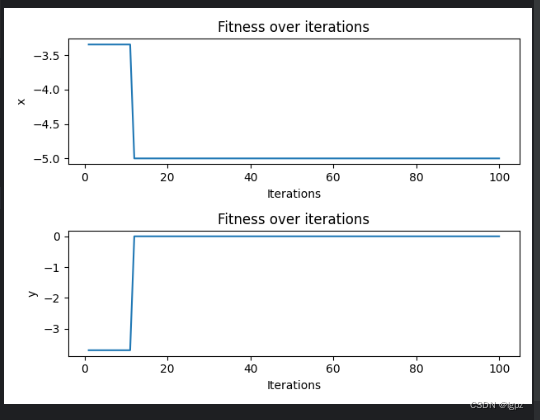
解释

这里利用粒子群算法完成对目标函数x2+y2=25的优化求解。
实现了较标准的粒子群算法，包括r1、r2在0到1的随机化，w的渐变。最大粒子速度推荐自变量范围的10%~20%，这里取20%。