- 1hive进阶 技巧
- 2SSRF 302跳转 gopher协议攻击redis写入ssh公钥,实现远程无密登录(学习总结)
- 3java数组的基础知识点总结_java数组知识点总结
- 4Android APK反编译就这么简单 详解(附图),2024年Android开发实战
- 5HCIP Datacom - 821 题库(二)_hcip题库2023
- 6代码千行不如架构图一张!程序员如何培养业务思维,做有价值的需求?
- 7项目学习
- 8三步,本机白嫖 Stable Diffusion 3 模型!附操作手册_stable diffusion v3.0
- 9Django和HarmonyOS-FA模型ArkTS语言的登录功能实现_deveco studio怎么实现登陆
- 10python程序设计语言超详细知识总结_python程序语言
【原理与代码讲解】遗传算法 GA(基础版)_ga算法代码
赞
踩
0 前言
Gitee 代码地址:https://gitee.com/futurelqh/GA
1. 背景

2. 相关术语

3. 执行流程

4. 理论与代码细节
4.1 编码
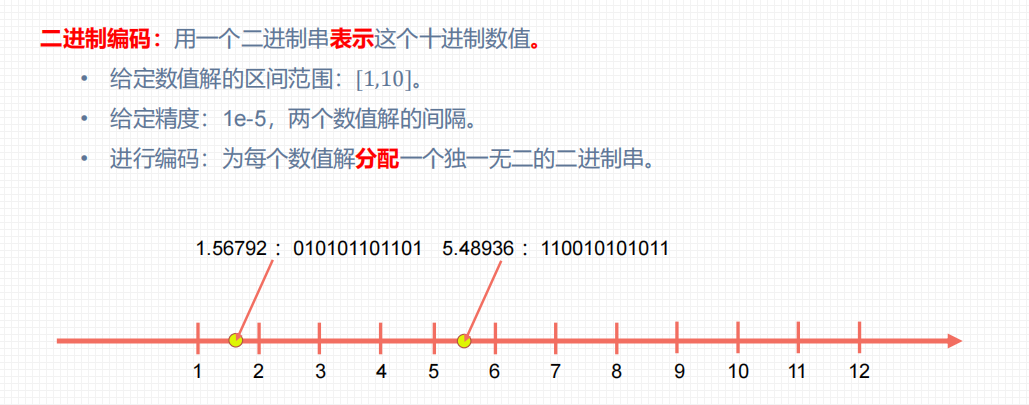

4.2 解码

%% 二进制转十进制并求出对应解函数
function dec = bintodec( pop ,popsize, chromlength,xlim )
% pop:二维,每行位每个群体对应的二进制串
% popsize: 种群个数
% chromlength:串的长度
% xlim :一维,解空间的上下限
dec = zeros(1,chromlength);
index = chromlength-1:-1:0;
for i = 1 : popsize
dec(i) = sum(pop(i,:).* (2.^index));
end
dec = xlim(1) + dec*( xlim(2) - xlim(1) ) /( 2 ^ chromlength - 1) ;
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
4.3 复制

function newx = copyx1(pop, fitvalue, popsize) % pop:二维,每行位每个群体对应的二进制串 % fitvalue: 一维,对应每个种群的适应度 % popsize:种群数量 % 按照 轮盘赌策略 对个体进行选择 chooseN = 5; % 选择个体数 sumFitness = sum(fitvalue); accp = ones(1, chooseN) .* cumsum(fitvalue ./ sumFitness); randVal = rand(1, popsize) .* ones(chooseN, 1); candidate = (popsize + 1) - sum(randVal <= accp); newx = pop(candidate,:); end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
4.4 交叉

代码案例选择 12 、34 、56 交叉方式,随机选择交叉位点(其他交叉方式均可)
执行流程: 判断是否执行交叉操作,如执行则依次选出两个个体,x1, x2, 然后利用 randperm产生两个随机数,作为位点,对 r1 ~ r2 区间的串进行交叉,即交换操作。最终复制给 newx
%% 交叉操作 function newx = crossover(pop, pc, popsize,chromlength ) % pop:二维,每行为每个群体对应的二进制串 % pc:交叉概率 % popsize:种群数量 % chromlength:二进制串长度 % 12 34 56交叉方式,随机选择交叉位点 % 注意个体数为奇数偶数的区别 i = 2 ; newx = pop ; % 申请空间 while i + 2 <= popsize %将第i 与 第 i -1 进行随机位点交叉 if rand < pc % 这里直接使用 rand 在每一轮均会产生不同的随机数 disp(rand) x1 = pop(i-1,:); x2 = pop(i,:) ; r = randperm( chromlength , 2 ) ; % 从 1 到 chromlength之间,随机返回 2 个整数 r1 = min(r); r2 =max(r) ; % 交叉复制的位点,r1:低位,r2:高位 % x1( 1 : r1-1) :第一段染色体的前半段,拼接上 x2(r1:r2) :第二个染色体的交换部分,凭借上自身的后半部分:x1(r2+1: end) newx(i-1,:) = [x1( 1 : r1-1),x2(r1:r2) , x1(r2+1: end)]; newx(i , : ) = [x2( 1 : r1-1),x1(r1:r2) , x2(r2+1: end)]; end i = i + 2 ; %更新i end end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
优化为矩阵操作
function f = f_crossover(newpop,pc,popsize,chromlength) % newpop 个体;pc 交换概率;popsize 染色体个数;chromlength 染色体长度 f = newpop; f2 = newpop; % 将 newpop 整体后移存储到 f2 f2(1,:) = f2(popsize,:); f2(2:popsize,:) = newpop(1:popsize-1,:); % 随机提取需要进行交换的个体 idx = find(rand(popsize,1) <= pc); % 双点交换获取上下线 bds = 1+round(rand(popsize,2)*(chromlength-1)); lb = min(bds,[],2); rb = max(bds,[],2); % 进行等位基因的替换 f(idx,lb:rb) = f2(idx,lb:rb); end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
4.5 变异

%% 变异 function newx = mutation(pop,pm, popsize,chromlength) % pop:二维,每行为每个群体对应的二进制串 % pm:变异概率 % popsize:种群数量 % chromlength:二进制串长度 i = 1 ; while i <= popsize if rand < pm r = randperm( chromlength , 1 ) ; % 随机产生一个位点 pop(i , r) = ~pop(i, r); % 进行取反操作 end i = i + 1; end newx = pop; %将变异后的结果返回。 end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
优化为矩阵操作
function newx = mutation3(pop,pm, popsize,chromlength) r = rand(1, popsize) < pm; % 产生随机值选出进行变异的个体 inx = find(r == 1); % 存储变异个体的原索引 new = pop(r,:); % 取出变异个体的值组成新的矩阵 count = size(new); % 获取变异个体矩阵的行列值 position = round(rand(1,count(1))*chromlength + 1); % 对每个个体进行随机位置索引变异 position(position > chromlength) = chromlength; new(sub2ind(size(new), [1:count(1)]', position')) = ~new(sub2ind(size(new), [1:count(1)]', position')); % 变异位置取反 pop(inx,:) = new; % 替换原位置 newx = pop; end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
4.6 复制中的轮盘赌操作


上述解释: 对适应度求出的概率进行累和得到 Cs 后,利用 rand 产生轮盘赌的随机数,然后排序依次判断,j 指针用于控制轮盘赌,i 指针用于循环判段每个个体是否满足复制条件,满足则进行复制,并使得 轮盘赌指针 j + 1,继续判断当前个体是否还可以继续复制。详细过程见下

执行细节: 图中例举种群有 4 个个体,首先利用适应度计算每个个体的概率 pi,然后对每个个体求累加和,结果为 0.2, 0.3, 0.7, 1.0,此时利用 rand 函数产生轮盘转动用于判断每轮转动指向那个具体的个体,产生 4 个随机数后,对其排序,例如:0.1, 0.5, 0.6, 0.8,然后依次循环判断,j 作为轮盘概率的指针,i 作为原始的个体,首先第一轮, R = 0.1, 此时第一个个体的概率为 0.2,在 0 ~ 0.2 范围内,进行复制操作,newx(1) = oldx(1), j + 1, 此时 i = 1, j = 2,第二轮,R = 0.5,此时 Cs(1) = 0.2, R > Cs,不复制,i + 1,为 2,判断下一个,Cs = 0.3, R > Cs,不复制,i + 1,为 3,判断下一个,此时 Cs(3) = 0.7,即 0.3 ~ 0.7 范围,R = 0.5,在此范围,对 3 进行复制,new(2) = old(3),循环往复。
%% 复制操作 function newx = copyx(pop, fitvalue,popsize ) % 传进来二进制串和对应适应度 % pop:二维,每行位每个群体对应的二进制串 % fitvalue: 一维,对应每个种群的适应度 % popsize:种群数量 % 按照 上述讲解 的轮盘赌策略对个体复制 newx = pop; %只是起到申请一个size为 pop 大小空间的作用,newx 之后要更新的 i = 1; j = 1; p = fitvalue / sum(fitvalue) ; Cs = cumsum(p) ; R = sort(rand(popsize,1)) ; % 每个个体的复制概率 while j <= popsize if R(j) < Cs(i) newx(j,:) = pop(i,:) ; j = j + 1; else i = i + 1; end end end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
优化为矩阵操作
%% 解码函数
function dec = bintodec(pop ,popsize, chromlength,xlim )
% pop:二维,每行位每个群体对应的二进制串
% popsize: 种群个数
% chromlength:串的长度
% xlim :一维,解空间的上下限
dec = zeros(1,chromlength); % 初始化
index = chromlength-1:-1:0; % 二进制从后往前算
dec = (pop * (2.^index)')'; % 十进制结果
dec = xlim(1) + dec*( xlim(2) - xlim(1) ) /( 2 ^ chromlength - 1); % 计算最终的解码精度
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
4.6 整个过程的代码
解码操作: bintodec.m
%% 解码函数 function dec = bintodec(pop ,popsize, chromlength,xlim ) % pop:二维,每行位每个群体对应的二进制串 % popsize: 种群个数 % chromlength:串的长度 % xlim :一维,解空间的上下限 dec = zeros(1,chromlength); % 初始化 index = chromlength-1:-1:0; % 二进制从后往前算 dec = (pop * (2.^index)')'; % 十进制结果 dec = xlim(1) + dec*( xlim(2) - xlim(1) ) /( 2 ^ chromlength - 1); % 计算最终的解码精度 end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
目标函数: calobjvalue.m
%% 目标函数
function fx = calobjvalue(decpop ) %参数为十进制解
f = @(x) abs(x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x) +3 * x .* sin(4 * x)) ; % 研究对象函数
fx = f(decpop);
end
- 1
- 2
- 3
- 4
- 5
- 6
适应度计算: calfitvalue.m
%% 计算适应度
function fitvalue = calfitvalue(fx)
%这里求最大值,并且函数值又都大于0,所以直接使用函数值本身作为适应度值。
% 事实上,不同的问题适应度函数构造方法多种多样。
fitvalue = fx ;
end
- 1
- 2
- 3
- 4
- 5
- 6
复制操作: copyx.m
function newx = copyx1(pop, fitvalue, popsize) % pop:二维,每行位每个群体对应的二进制串 % fitvalue: 一维,对应每个种群的适应度 % popsize:种群数量 % 按照 轮盘赌策略 对个体进行选择并复制 chooseN = 5; % 选择个体数 sumFitness = sum(fitvalue); accp = ones(1, chooseN) .* cumsum(fitvalue ./ sumFitness); randVal = rand(1, popsize) .* ones(chooseN, 1); candidate = (popsize + 1) - sum(randVal <= accp); newx = pop(candidate,:); end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
交叉操作: crossover.m
%% 交叉操作 function f = f_crossover(newpop,pc,popsize,chromlength) % newpop 个体;pc 交换概率;popsize 染色体个数;chromlength 染色体长度 f = newpop; f2 = newpop; % 将 newpop 整体后移存储到 f2 f2(1,:) = f2(popsize,:); f2(2:popsize,:) = newpop(1:popsize-1,:); % 随机提取需要进行交换的个体 idx = find(rand(popsize,1) <= pc); % 双点交换获取上下线 bds = 1+round(rand(popsize,2)*(chromlength-1)); lb = min(bds,[],2); rb = max(bds,[],2); % 进行等位基因的替换 f(idx,lb:rb) = f2(idx,lb:rb); end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
变异操作: mutation.m
%% 变异 function newx = mutation3(pop,pm, popsize,chromlength) r = rand(1, popsize) < pm; % 产生随机值选出进行变异的个体 inx = find(r == 1); % 存储变异个体的原索引 new = pop(r,:); % 取出变异个体的值组成新的矩阵 count = size(new); % 获取变异个体矩阵的行列值 position = round(rand(1,count(1))*chromlength + 1); % 对每个个体进行随机位置索引变异 position(position > chromlength) = chromlength; new(sub2ind(size(new), [1:count(1)]', position')) = ~new(sub2ind(size(new), [1:count(1)]', position')); % 变异位置取反 pop(inx,:) = new; % 替换原位置 newx = pop; end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
绘图: plotfig.m
%% 绘制图像
function plotfig(decpop , fx ,xlim,k)
f = @(x) abs(x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x) +3 * x .* sin(4 * x)); % 研究对象函数
x = xlim(1):0.05:xlim(2);
y = f(x) ;
subplot(1,2,1);
plot(x,y,decpop,fx,'o')
title(['第',num2str(k),'次迭代进化'])
%pause(0.2)
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
遗传算法: GA.m
%%主程序 clear close all popsize=20; % 群体大小 chromlength=20; %串的长度(个体长度) pc=0.6; %交叉概率 pm=0.1; %变异概率 xlim = [0,50]; G = 100 ; %迭代次数 % x = zeros(1,G); % 记录每代个体最优位置 % y = zeros(1,G); % 记录每代最优个体对应的函数值 pop= round( rand(popsize,chromlength) ) ; %随机产生初始群体 decpop = bintodec( pop ,popsize, chromlength,xlim ) ; % 计算初代解对应十进制 fx = calobjvalue(decpop ) ; % 计算初代解的函数值 plotfig(decpop , fx , xlim , 1 ) ; % 绘制图像 [y(1) , l ] = min(fx); x(1) = decpop(l); for i=2 : G decpop = bintodec( pop , popsize, chromlength,xlim ) ; % 计算上一代解对应十进制 fx = calobjvalue(decpop ) ; % 计算上一代解的函数值 fitvalue = calfitvalue(fx) ; % 适应度映射 newpop = copyx(pop,fitvalue,popsize); % 复制 newpop = crossover(newpop, pc, popsize,chromlength ); % 交叉 newpop = mutation(newpop,pm, popsize,chromlength); % 变异 % 这时的newpop是经过复制交叉变异产生的新一代群体 % 下边进行选择择优保留(即实现保底机制) newdecpop = bintodec( newpop ,popsize, chromlength,xlim ) ; % 进行解码操作 new_fx = calobjvalue(newdecpop) ; %计算每个个体新解目标函数 new_fitvalue = calfitvalue(new_fx); %计算新群体中每个个体的适应度,这里就是目标函数的解 index = find(new_fitvalue > fitvalue) ; % 判断当前适应度是否 > 上一代的适应度,返回下标 pop(index, : ) = newpop(index,:) ; % 更新得到最新解 decpop = bintodec( pop ,popsize, chromlength,xlim ) ; %计算新解的解码结果 fx = calobjvalue( decpop ) ; % 计算结果 plotfig(decpop , fx ,xlim , i ) % 绘制新解的图 % 找出更新后的个体最优函数值 [bestindividual,bestindex] = max( fx ) ; y(i) = bestindividual; % 记录每一代的最优函数值 x(i) = decpop(bestindex) ; % 解码二进制串 subplot(1,2,2); plot(1:i,y); title('适应度进化曲线'); i = i + 1 ; end [ymax, max_index] = max(y); disp(['找的最优解位置为:', num2str(x(max_index)) ]) disp(['对应最优解为:', num2str(ymax) ])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
遗传算法: GA.m (多变量)
%% 粒子群算法PSO: 求解函数 f1(x)=sum(x(i)^2) 在[-5.12,5.12]内的最小值 clear close all var = 3 % 变量个数 popsize=5; % 群体大小 chromlength=5; % 串的长度(个体长度) pc=0.6; % 交叉概率 pm=0.1; % 变异概率 xlim = [-5.12,5.12]; iter = 1000 ; % 迭代次数 pop= round( rand(popsize,var * chromlength) ); % 随机产生初始群体 % 初始化记录每一轮的最优适应度 y = zeros(1, iter); for i = 1 : iter for j = 1 : var decpop(: , j) = bintodec(pop(:, (j - 1) * chromlength + 1 : j * chromlength), popsize, chromlength, xlim); % 计算上一代解对应实数 end fx = Obj_fun1(decpop); % 计算上一代解的函数值 fitvalue = calfitvalue(fx); % 适应度映射 newpop = copyx1(pop,fitvalue,popsize); % 轮盘赌个体选择 newpop = f_crossover(newpop, pc, popsize,chromlength ); % 交叉 newpop = mutation3(newpop,pm, popsize,chromlength); % 变异 % --------- 经过复制交叉变异产生的新一代群体,进行更新筛选 --------------- % 进行解码操作 for j = 1 : var newdecpop(: , j) = bintodec(newpop(:, (j - 1) * chromlength + 1 : j * chromlength), popsize, chromlength, xlim); % 计算上一代解对应实数 end new_fx = Obj_fun1(newdecpop) ; %计算每个个体新解目标函数 new_fitvalue = calfitvalue(new_fx); %计算新群体中每个个体的适应度,这里就是目标函数的解 index = find(new_fitvalue < fitvalue) ; % 判断当前适应度是否 < 上一代的适应度,返回下标 pop(index, : ) = newpop(index,:) ; % 更新得到最新解 % 进行解码操作 for j = 1 : var decpop(: , j) = bintodec(pop(:, (j - 1) * chromlength + 1 : j * chromlength), popsize, chromlength, xlim); % 计算上一代解对应实数 end fx = Obj_fun1(decpop) ; % 计算结果 fxvalue = calfitvalue(fx); % 找出更新后的个体最优函数值 [bestindividual,bestindex] = min( fxvalue ); y(i) = bestindividual; % 记录每一代的最优函数值 x(i) = decpop(bestindex) ; % 解码二进制串 i = i + 1 ; end plot(1:iter,y); hold on; title('适应度进化曲线'); [ymax, max_index] = min(y); disp(['找的最优解位置为:', num2str(x(max_index)) ]) disp(['对应最优解为:', num2str(ymax) ])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92



