机器学习算法（6）——随机森林_随机森林 最小均方差原则

随机森林（Random Forests）

           随机森林是一种重要的基于Bagging的集成学习方法，可以用来做分类、回归等问题。要学随机森林，先简单介绍一下集成学习方法和决策树算法。

Bagging和Boosting的概念与区别

     随机森林属于集成学习（Ensemble Learning）中的bagging算法。在集成学习中，主要分为bagging算法和boosting算法。我们先看看这两种方法的特点和区别。

Bagging（套袋法）

       bagging的算法过程如下：从原始样本集中使用Bootstraping方法随机抽取n个训练样本，共进行k轮抽取，得到k个训练集。（k个训练集之间相互独立，元素可以有重复）
      对于k个训练集，我们训练k个模型（这k个模型可以根据具体问题而定，比如决策树，knn等）对于分类问题：由投票表决产生分类结果；对于回归问题：由k个模型预测结果的均值作为最后预测结果。（所有模型的重要性相同）
 

Boosting（提升法）

     boosting的算法过程如下：对于训练集中的每个样本建立权值wi，表示对每个样本的关注度。当某个样本被误分类的概率很高时，需要加大对该样本的权值。
     进行迭代的过程中，每一步迭代都是一个弱分类器。我们需要用某种策略将其组合，作为最终模型。（例如AdaBoost给每个弱分类器一个权值，将其线性组合最为最终分类器。误差越小的弱分类器，权值越大）

Bagging，Boosting的主要区别：

样本选择上：Bagging采用的是Bootstrap随机有放回抽样；而Boosting每一轮的训练集是不变的，改变的只是每一个样本的权重。
样本权重：Bagging使用的是均匀取样，每个样本权重相等；Boosting根据错误率调整样本权重，错误率越大的样本权重越大。
预测函数：Bagging所有的预测函数的权重相等；Boosting中误差越小的预测函数其权重越大。
并行计算：Bagging各个预测函数可以并行生成；Boosting各个预测函数必须按顺序迭代生成。

下面是将决策树与这些算法框架进行结合所得到的新的算法：

1）Bagging + 决策树 = 随机森林

2）AdaBoost + 决策树 = 提升树

3）Gradient Boosting + 决策树 = GBDT

原文：https://blog.csdn.net/qq547276542/article/details/78304454 

决策树

    常用的决策树算法有ID3，C4.5，CART三种。3种算法的模型构建思想都十分类似，只是采用了不同的指标，ID3算法基于香农熵；C4.5算法基于增益比；而CART算法基于Gini不纯度。

只简单介绍下CART与ID3和C4.5的区别。

1. CART树是二叉树，而ID3和C4.5可以是多叉树
2. CART在生成子树时，是选择一个特征一个取值作为切分点，生成两个子树
3. 选择特征和切分点的依据是基尼指数，选择基尼指数最小的特征及切分点生成子树
4. 具体参见博客：https://blog.csdn.net/qq_30815237/article/details/86555954

---

随机森林算法工作原理

      随机森林是一种有监督学习算法。 就像你所看到的它的名字一样，它创建了一个森林，并使它拥有某种方式随机性。 所构建的“森林”是决策树的集成，大部分时候都是用“bagging”方法训练的。 bagging方法，即bootstrap aggregating，采用的是随机有放回的选择训练数据然后构造分类器，最后组合学习到的模型来增加整体的效果。

      简而言之：随机森林建立了多个决策树，并将它们合并在一起以获得更准确和稳定的预测。随机森林的一大优势在于它既可用于分类，也可用于回归问题，这两类问题恰好构成了当前的大多数机器学习系统所需要面对的。 接下来，将探讨随机森林如何用于分类问题，因为分类有时被认为是机器学习的基石。 下图，你可以看到两棵树的随机森林是什么样子的：

               

                

      随机森林算法中树的增长会给模型带来额外的随机性。与决策树不同的是，每个节点被分割成最小化误差的最佳特征，在随机森林中我们选择随机选择的特征来构建最佳分割。因此，当您在随机森林中，仅考虑用于分割节点的随机子集，甚至可以通过在每个特征上使用随机阈值来使树更加随机，而不是如正常的决策树一样搜索最佳阈值。这个过程产生了广泛的多样性，通常可以得到更好的模型。

一个更容易理解算法的例子

     想象一下，一个名叫安德鲁的人，想知道一年的假期旅行中他应该去哪些地方。他会向了解他的朋友们咨询建议。起初，他去寻找一位朋友，这位朋友会问安德鲁他曾经去过哪些地方，他喜欢还是不喜欢这些地方。基于这些回答就能给安德鲁一些建议，这便是一种典型的决策树算法。朋友通过安德鲁的回答，为其制定出一些规则来指导应当推荐的地方。随后，安德鲁开始寻求越来越多朋友们的建议，他们会问他不同的问题，并从中给出一些建议。 最后，安德鲁选择了推荐最多的地方，这便是典型的随机森林算法。

随机森林算法的特征的重要性

      随机森林算法的另一个优点是可以很容易地测量每个特征对预测的相对重要性。 Sklearn为此提供了一个很好的工具，它通过查看使用该特征减少了森林中所有树多少的不纯度，来衡量特征的重要性。它在训练后自动计算每个特征的得分，并对结果进行标准化，以使所有特征的重要性总和等于1。

       通过查看特征的重要性，您可以知道哪些特征对预测过程没有足够贡献或没有贡献，从而决定是否丢弃它们。这是十分重要的，因为一般而言机器学习拥有的特征越多，模型就越有可能过拟合，反之亦然。

from：http://www.elecfans.com/d/647463.html

随机森林的构建过程

与上面介绍的Bagging过程相似，随机森林的构建过程大致如下：

从原始训练集中使用Bootstraping方法随机有放回采样选出m个样本，共进行n_tree次采样，生成n_tree个训练集；
对于n_tree个训练集，我们分别训练n_tree个决策树模型；
对于单个决策树模型，假设训练样本特征的个数为n，每次分裂时根据信息增益/信息增益比/基尼指数选择最好的特征进行分裂；
每棵树都一直这样分裂下去，直到该节点的所有训练样例都属于同一类。在决策树的分裂过程中不需要剪枝；
将生成的多棵决策树组成随机森林。对于分类问题，按多棵树分类器投票决定最终分类结果；对于回归问题，由多棵树预测值的均值决定最终预测结果。
原文：https://blog.csdn.net/qq547276542/article/details/78304454 

随机森林回归和分类的不同：

随机森林可以应用在分类和回归问题上。实现这一点，取决于随机森林的每颗cart树是分类树还是回归树。

• 如果cart树是分类数，那么采用的计算原则就是gini指数。随机森林基于每棵树的分类结果，采用多数表决的手段进行分类。
• 如果是回归树，则cart树是回归树，采用的原则是最小均方差。即对于任意划分特征A，对应的任意划分点s两边划分成的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为：

                                      
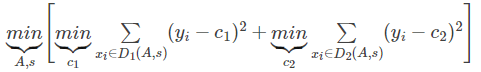
其中，c1为D1数据集的样本输出均值，c2为D2数据集的样本输出均值。 cart树的预测是根据叶子结点的均值，因此随机森林的预测是所有树的预测值的平均值。