Python算法学习day6:堆排序(topK问题)_python topk堆排序

堆

在学习堆排序之前,先必须了解一下什么是堆

堆是具有以下性质的完全二叉树：

每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

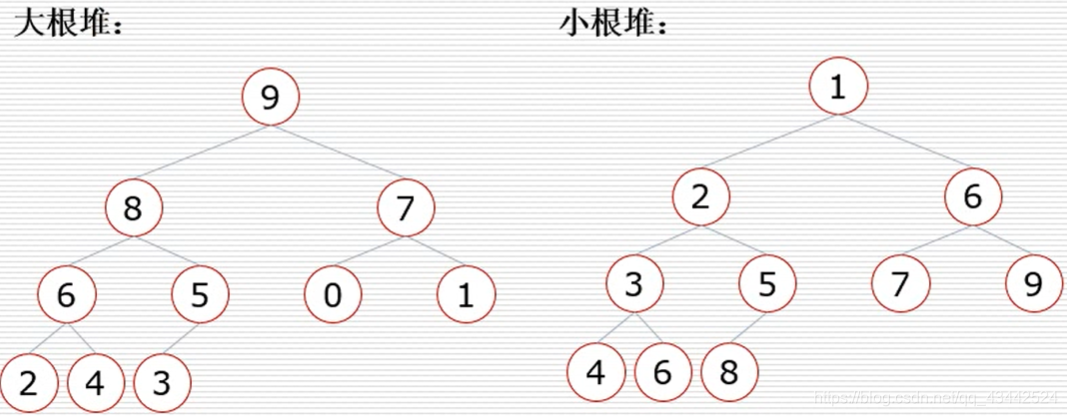
而二叉树中,父节点与左右孩子节点的编号下标都有一定的关系:
其中父节点与左孩子节点的关系是 i -> 2i+1, 父节点与右孩子节点的关系是 i -> 2i+2

注: 这里指节点的下标关系

(1) 堆的向下调整性质

假设: 节点的左右字数都是堆,但自身不是堆

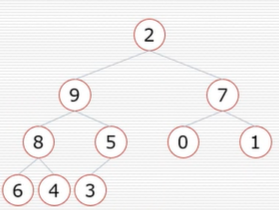
当根节点的左右字数都是堆时,可以通过一次向下的调整来将其变换成一个堆

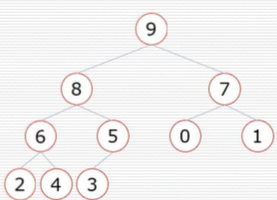
(2) 挨个出数

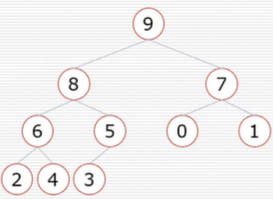
9是堆中数字最大,将9取出,为保证完全二叉树,将树中最后的数字3添加到头部.

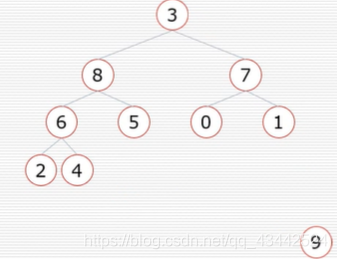
接下来向下调整

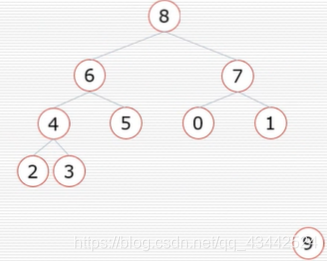
依次取数便取出一个升序列表

堆排序的平均时间复杂度为 Ο(nlogn)

(3) 堆的算法步骤

1. 创建一个堆 H[0……n-1]；

2. 把堆首（最大值）和堆尾互换；

3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；

4. 重复步骤 2，直到堆的尺寸为 1。

来源：https://github.com/hustcc/JS-Sorting-Algorithm

(4) 算法实现

def sift(li, low, high):
	# li表示数, low表示树根, high表示树最后一个节点的位置
	tmp = li[low]
	i = low
	j = 2 * i + 1 # 指向左孩子
	# i指向空位, j表示两个孩子
	while j <= high: # 循环退出的第二种情况: j > high, 说明空位i是叶子节点
		if j+1 <= high and li[j] < li[j+1]: # 如果右孩子存在并且比左孩子大, 指向右孩子
			j += 1
		if li[j] > tmp:
			li[i] = li[j]
			i = j
			j = 2 * i + 1
		else: # 循环退出的第一种情况, j位置的值比tmp小, 说明两个孩子都比tmp小
			break
	li[i] = tmp

def heap_sort(li):
	n = len(li)
	# 1. 构造堆
	for low in range(n//2-1, -1, -1):
		sift(li, low ,n-1)
	# 2. 挨个出数
	for high in range(n-1, -1, -1):
		li[0], li[high] = li[high], li[0]
		sift(li, 0, high - 1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
'
运行
运行

(5)例题: topK问题

问题:现在有n个数, 设计算法找出前k大的数(k<n)

解决方法:

1. 排序后切片

li.sort(reverse=True)[:k-1]
1

2. 堆排序

import heapq


def heapsort(data, hp_size):
    h = []
    for i in range(len(data)):
        if i >= hp_size:
            heapq.heappushpop(h, data[i])
        else:
            heapq.heappush(h, data[i])
    return [heapq.heappop(h) for _ in range(len(h))]

1
2
3
4
5
6
7
8
9
10
11
12
'
运行
运行