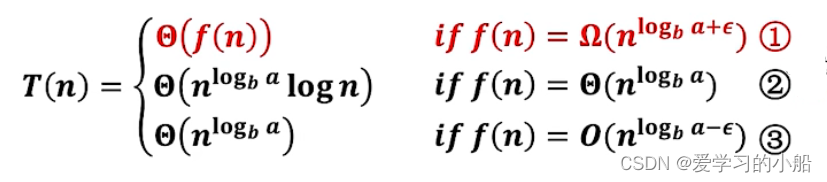
        也就是在比较合并成本和叶子成本，究竟谁更大。粗略的理解如下：
        ① f(n)多项式意义大于 $n^{\log_{b} a }$ ，不止渐进大于且相差n^ε，所以总体代价以f(n)为主；（这里忽略了对正则条件的理解，感觉不影响使用，想了解深层原理可以看一下课本）
②  f(n)与 $n^{\log_{b} a }$ 等阶，最后的结果要再乘以logn
③ f(n)多项式意义小于 $n^{\log_{b} a }$ ，不止渐进小于且相差n^ε，所以总体代价为 $n^{\log_{b} a }$

这三种情况画在线段上如下图所示，所以中间哪些无法覆盖的部分就是这个定理无法涵盖的情况。具体的讲解还是可以看看那个北航老师的视频。

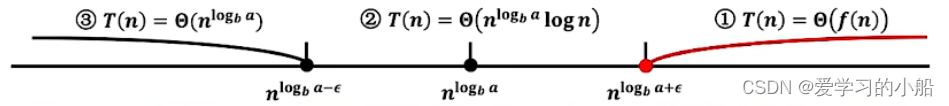
2. 主定理法的应用

例1：求解递推方程T(n) = 9T(n/3)+n

解：上述递推方程中，a=9, b=3, f(n) = n
$n^{\log_{b} a }$ = $n^{\log_{3}9}$ = n²， $f(n) = O(n^{\log_{3}9 -1})$ ，ε取1
所以，T(n) = Θ(n²)

分析：在这个题中，a=9, b=3, f(n) = n，先求 $n^{\log_{b} a }$ = $n^{\log_{3}9}$ = n²
（再与 f(n)进行对比，发现 $n^{\log_{b} a }$ 的次数高一些，所以最后的T(n)就是 n²,）
相当于 $f(n) = O(n^{\log_{3}9 -1})$ 也是就上述的情况③，ε取1，T(n) = Θ(n²)

例2：求解递推方程T(n) = T(2n/3)+1

解：上述递推方程中，a=1, b=3/2, f(n) = 1
$n^{\log_{b} a }$ = $n^{\log_{3/2}1}$ = n^0=1，
所以，T(n) = Θ(log n)

分析：在这个题中，a=1, b=3/2, f(n) = 1，先求 $n^{\log_{b} a }$ = 1
（再与 f(n)进行对比，发现与 $n^{\log_{b} a }$ 的次数一样，
也是就上述的情况②，所以最后的T(n)就是 $n^{\log_{b} a }$ *log n,
即 T(n) = Θ(log n)

例3：求解递推方程T(n) = 3T(n/4)+nlogn

解：上述递推方程中，a=3, b=4, f(n) = nlogn

取ε = 0.2，则T(n) = nlogn

分析：在这个题中，a=3, b=4, f(n) = ，先求 $n^{\log_{b} a }$ = $n^{\log_{4}3}$ 次数是比 n小的，
再与 f(n)进行对比，发现 f(n)中 n 的部分是1次方，比 $n^{\log_{b} a }$ 的大，所以f(n)占主导
也是就上述的情况1，所以最后的T(n)就是f(n),
即 T(n) = Θ(n log n)

不能使用主定理的：

例4：T(n)=2T(n/2)+nlogn

分析：在这个题中，a=2, b=2, f(n) = nlogn，先求 $n^{\log_{b} a }$ = n
（再与 f(n)进行对比，发现f(n) 的 n 部分与 $n^{\log_{b} a }$ 的次数一样，但是多了logn

这种情况，等于落入了①和②之间的红点，就是不满足使用主定理的，可以考虑使用拓展定理

总体来看，从只考虑做题的角度理解例3和例4，就是：比较 $n^{\log_{b} a }$ 与f(n) 中n 的次数，先不管f(n)中的 logn ，如果f(n)的次数高，就取f(n)，如果 $n^{\log_{b} a }$ 的次数高，就取 $n^{\log_{b} a }$ ，
但是如果f(n)中的n的次数与 $n^{\log_{b} a }$ 相等，然后f(n)还有logn 的部分，就属于是主定理一般情况无法解决的了，可以用递归树，也可以用主定理的扩展形式。

3. 主定理的扩展形式

扩展形式中，对于情况②，增加了 $\log^{k}_{}n$ ，也就是说，如果遇到f(n)的n的次方与 $n^{\log_{b} a }$ 相等，哪怕f(n)有log n 的部分，总体的T(n) 还是f(n) 再乘一个 log n，画在线段中，也就是多了以下的一些点的情况。

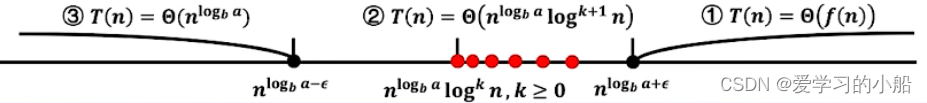
还看例4：T(n)=2T(n/2)+nlogn

解： a=2, b=2, f(n) = nlogn，先求 $n^{\log_{b} a }$ = n
f(n) = Θ( $n^{\log_{b} a }$ $\log^{k}_{}n$ )， k=1
T(n) = Θ( $n^{\log_{b} a }$ $log^{k+1}n$ ) = Θ( $n log^{2}n$ )

参考链接：
北航老师的讲解视频：[2.2.2]--2.2递归式求解下_哔哩哔哩_bilibili

一个写的很清楚的博客：

【算法设计与分析】12 主定理及其应用_杨柳_的博客-CSDN博客_t(n)=3t(n/4)+nlogn

有例题的文档：2.8.主定理的应用 - 豆丁网

关于一个疑问的解答：

T(n)=3T(n/4)+nlgn与T(n)=2T(n/2)+nlgn在主定理的应用上有什么区别？ - 知乎

2.4 分治法的使用条件

（1）问题缩小到一定的规模（子问题）时易解决

（2）原问题与分解后的子问题同类（即该问题具有最优子结构性质）

（3）原问题的解可以由子问题的解合并得到

（4）子问题相互独立，不包含公共问题。

2.5 分治法实例

2.5.1 快速排序

1、过程：
分解：根据选取的主元大小，将数组分成两部分，[p …… q-1] 和 [q+1 …… r]，是的前部分都小于这个主元A[q]，后半部分都大于A[q]

解决：递归调用快速排序算法，分别对分成的两段进行排序

合并：由于子数组是原地排序，所以合并的时候不需要操作

2、分治法的思想体现在：

挑主元，用主元作为基准元素，依次遍历数组，完成划分过程，这个划分的过程就是分治中标准的分解的过程

3、复杂度分析

快排：平均O(nlogn)，最坏情况O(n^2)

插入排序：将未排序的元素一个一个地插入到有序的集合中，插入时把所有有序集合从后向前扫一遍，找到合适的位置插入。最坏时间复杂度O(n^2)

归并排序：需要额外空间：O(n) 时间复杂度：O(nlogn)

快排的最坏时间复杂度产生的原因：

例如说主元每次都是最右边的元素，而这个数组本身又是递增的，那每次分解，都只能分解成长度为 n-1 和 1 的两个数组，相当于，每次遍历只能排好一个数组，每次都需要对n个元素进行遍历，并且要划分n次才能分好，复杂度就是O(n^2)

4、快排的随机版本

随机的选取主元，使得在概率上避免最坏情况

代码思路参考：

Acwing算法基础学习笔记（一）快排和归并_爱学习的小船的博客-CSDN博客

2.5.2 最大元最小元问题

1、问题描述

高级表述：给定n个数据元素，找出其中的最大元和最小元
翻译：就是求一个数组中的最大的数和最小的数

2、解题思路

如果直接求解，就是遍历整个数组，记一下最大或者最小的数，这样找到最大元需要n-1 次，再找最小元需要 n-2 次，总共需要 2n-3 次

先分析是否满足分治法的使用条件：

其实仔细想，可以发现，求一个数组的最大最小元，可以分成求子数组的最大最小值，然后再合并起来，他是拥有最优子结构并且子问题相互独立的，满足分治法的使用条件

所以就可以尝试一下分治法啦，先考虑特殊情况：
if n=1 ，就可以直接判断出，最大元和最小元

如果n>1，步骤还是考虑分治法的三部曲：

分解：将一个数组平均分成两份
求解：对左右两份数组都分别递归调用这个算法，求取每份的最大或者最小，直到数组只剩俩数或者一个数，底层就只需要一次
合并：合并的时候，比较左右两边的最大元和最小元
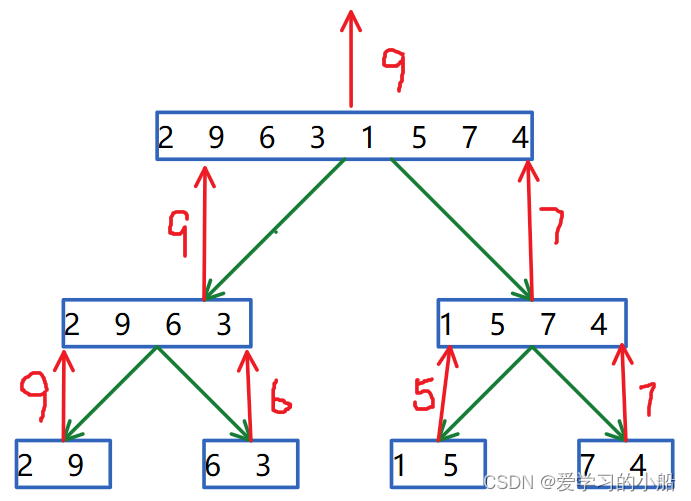
- 找最大元的过程如图所示：

3、分治法求数组最大元、最小元的算法下界

算法的复杂度是线性的，算法下界为3n/2-2。分析过程如图：

4、算法实现


#include <iostream>
using namespace std;
 
void findMaxMin(int str[], int l, int r,int &max, int &min)
{
    // 递归出口
	if(l==r){
		max = str[l];
		min = str[l];
	}else{
		int mid = (l + r) >> 1;
		int lmax,lmin,rmax,rmin; //分别记录两边的最大最小值
		
		//递归执行左右两段
		findMaxMin(str, l, mid, lmax,lmin);
		findMaxMin(str, mid+1, r, rmax, rmin);
        
        //合并比较左右的最大值最小值
		if(lmax >= rmax){
			max = lmax;
		}else{
			max = rmax;
		}
		if(lmin <= rmin){
			min = lmin;
		}else{
			min = rmin;
		}
	}
}
 
int main()
{
	int str[] = {2,9,6,3,1,5,7,4};
	int l = 0, r=7;
	int maxmin[] = {0,0};
	int max,min;
	findMaxMin(str, l, r, max, min);
	cout << "max:" <<max <<";min:"<< min;
	
	return 0;
}

2.5.3 最近点对

1、问题描述

就是求空间内，最近的两个点（最简单的就是一维问题，然后可以上升为二维的）

2、一维的最近点对的解题思路

同理，先分析是否满足分治法的适用条件：可以把空间分成两部分，求每个小空间的最近距离，但是在合并的时候，交界处比较难处理，但是也算是满足条件

分治法求解：
分解：用各个点坐标的中位数m 作为分割点，分成两个点集
解决：递归调用该算法，分别寻找两个点集上最接近的点对{p1, p2}、{q1, q2}及距离d1,d2
合并：整个点集的最近点对或者是{p1, p2}，或者是 {q1,q2}，或者是某个{p3,q3}，其中p3和q3分属两个点集（整个情况在合并的时候要仔细分析）

合并策略：
如果说两个点集的交界处有更近的点，那找到这俩个点，需要扫描的范围其实不会超过，两边的最近距离d的二倍，画个图如下所示，这2d的范围中，最多只可能会有4个点，如果说p1和p2之间还有其他的的点，那就会构成比d更近的距离了

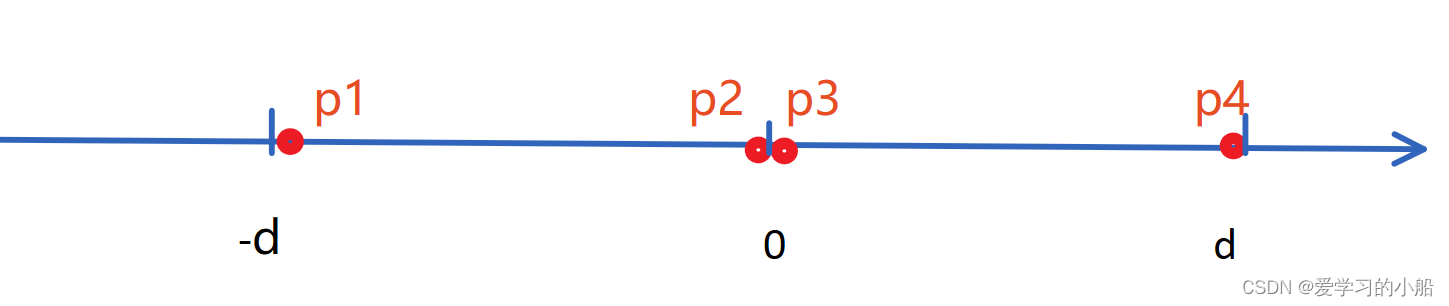
所以，合并的时候，我们需要在从分割点出发分别往左右扫描扫描到d的距离，看看是否会出现更近的情况就可以啦

3、二维最近点对问题的解题思路

有了一维的基础，再考虑二维的问题就好理解多了，直接来分治法求解过程：

（1）预处理：将点集P中的点，按照X Y坐标从小到大顺序排列

（2）分解：计算x坐标中位数m，选择一条垂线L:x=m，将点集P分成左右两部分PL和PR，分解到最后的递归出口，剩1~3个点时，就可以直接计算了

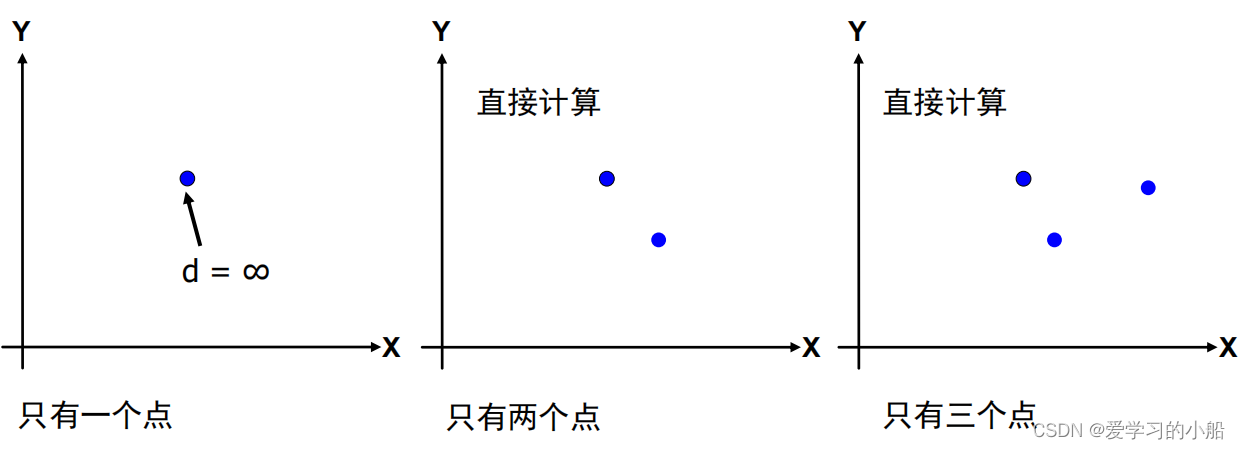
（3）解决：递归调用该算法，分别找PL和PR中的最近点对及距离，距离分别记为δL, δR，置δ = min(δL, δR)

（4）合并：考察带状区域中的点
① 找出以L为中心线，宽度为2声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】

《算法分析与设计》复习笔记_算法设计与分析笔记

一、算法的基本概念

1.1 算法的定义

1.2 算法的“好坏”如何衡量？

1.3 描述算法的时间复杂度 ⭐

1.4 如何评价算法

二、 分治法

2.1 分治法的求解步骤

2.2 平衡的概念

2.3 递归式解法

2.3.1 主定理法 ⭐

2.4 分治法的使用条件

2.5 分治法实例

2.5.1 快速排序

2.5.2 最大元最小元问题

2.5.3 最近点对

二、分治法