【蓝桥杯C/C++】专题六：动态规划_蓝桥杯动态规划

专题六：动态规划

在这里插入图片描述

导读

本专题将讲解最难理解的算法之一：动态规划。介绍动态规划的基本概念、算法原理以及应用场景。首先，我们将介绍动态规划的定义和特点，以及它与递归、贪心算法的区别。接着，我们将详细介绍动态规划的解题思路和算法流程，包括状态转移方程、边界条件、初始化等概念。最后，我们将讨论动态规划在实际问题中的应用，包括背包问题、最长公共子序列问题、最短路径问题等。

什么是动态规划

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题于最优子问题，使用动态规划是最有效的。

所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的.

例如：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动态规划中dp[j]是由dp[j-weight[i]]推导出来的，然后取max(dp[j], dp[j - weight[i]] + value[i])。

但如果是贪心呢，每次拿物品选一个最大的或者最小的就完事了，和上一个状态没有关系。

所以贪心解决不了动态规划的问题。

解决的问题

动态规划是一种数学方法，用于求解决策过程的最优化问题。如果一个问题可以分解成若干个子问题，并且子问题之间还有重叠的更小的子问题，就可以考虑使用动态规划来解决这个问题。应用动态规划之前要分析能否把大问题分解成小问题，分解后的每个小问题也存在最优解。如果将小问题的最优解组合起来能够得到整个问题的最优解，那么就可以使用动态规划解决问题。可以应用动态规划求解的问题主要具有以下四个特点：

• 问题是求最优解。
• 整体问题的最优解依赖于各个子问题的最优解。
• 大问题分解成若干小问题，这些小问题之间还有相互重叠的更小的子问题。
• 从上往下分析问题，从下往上求解问题。

解题步骤

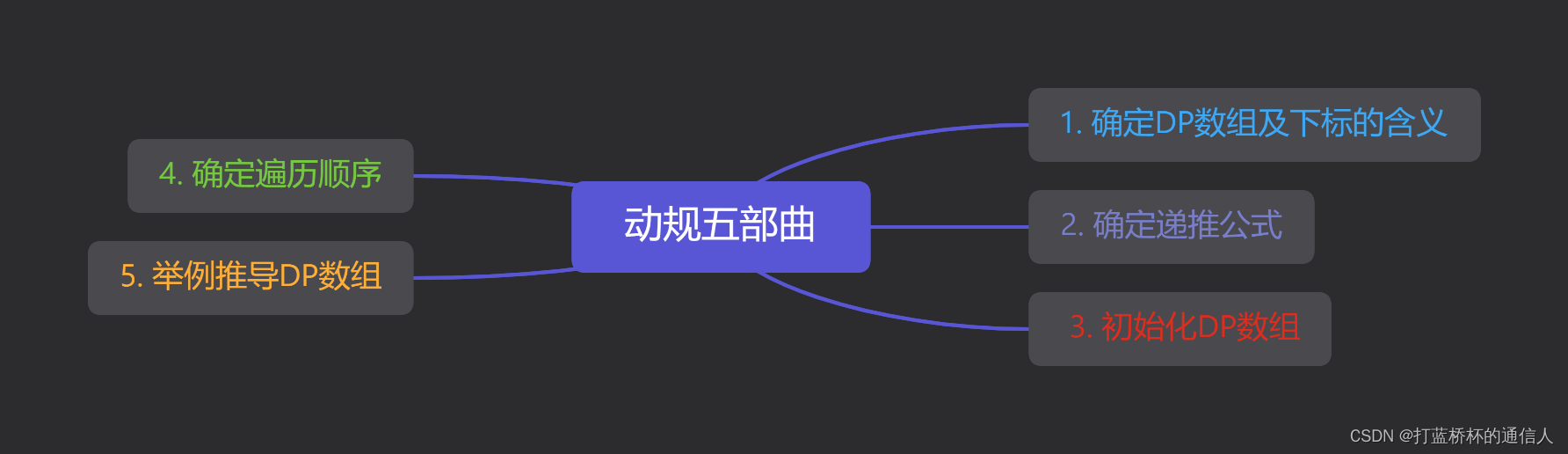
对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

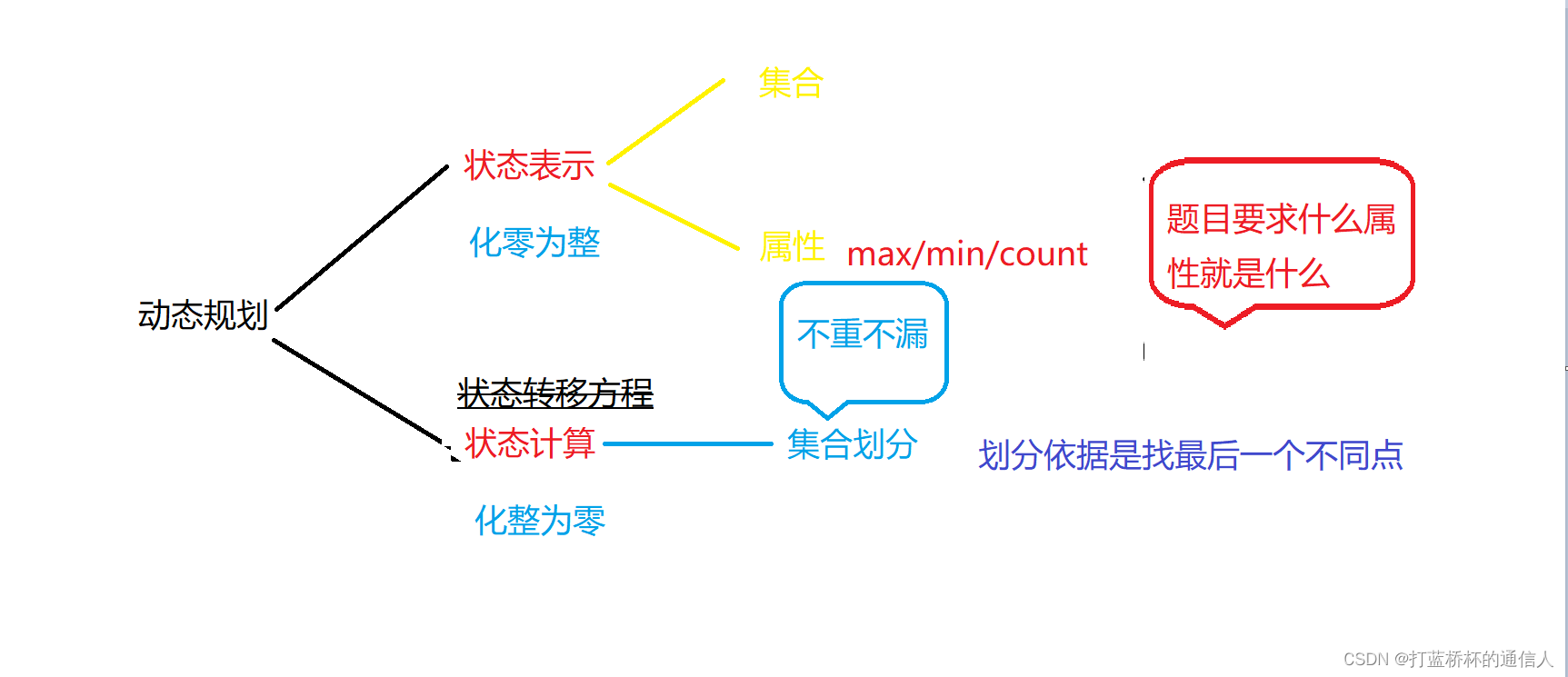
分享两张两种解决动态规划的思维导图：

动态规划应该如何debug

找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！

做动规的题目，写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。

然后再写代码，如果代码没通过就打印dp数组，看看是不是和自己预先推导的哪里不一样。

如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。

如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。

记忆化搜索

可以理解为实现dp的另一种方法，用递归实现本质还是搜索。

记忆化搜索按照自顶向下的顺序，每求得一个状态时，就把它的解保存下来，以后再次遇到这个状态时就不用重复求解了。

记忆化搜索包含两个要素记忆化和搜索。

• 沿用搜索的一般模式，本质还是用递归函数实现。
• 在搜索的过程中将已经得到的解保存起来，下次需要时直接用。

斐波那契数

题目

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入： n = 2
输出： 1
解释： F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入： n = 3
输出： 2
解释： F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入： n = 4
输出： 3
解释： F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

• 0 <= n <= 30

代码

class Solution {
public:
    int fib(int n) {
        if(n<2) return n;
       vector<int> dp(n+1);
       dp[0]=0;
       dp[1]=1;
       for(int i=2;i<=n;i++)
       {
           dp[i]=dp[i-1]+dp[i-2];
        //    cout<<dp[i]<<endl;
       }
       return dp[n];

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

题解

动态规划五部曲：

1. 确定dp数组以及下标的含义

   dp[i]定义为：第i个数的斐波那契值为dp[i]

2. 确定递推公式

   状态转移方程：dp[i]=dp[i-1]+dp[i-2]

3. dp数组如何初始化

   dp[0]=0; dp[1]=1;

4. 确定遍历顺序

   从前往后循环遍历，dp问题一般都是自底向上去思考。

爬楼梯

题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入： n = 2

输出： 2

解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： n = 3

输出： 3

解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

• 1 <= n <= 45

代码

class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针
        vector<int> dp(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是从3开始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

题解

爬到第一层楼梯有一种方法，爬到二层楼梯有两种方法。

那么第一层楼梯再跨两步就到第三层 ，第二层楼梯再跨一步就到第三层。

所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来，那么就可以想到动态规划了。

1. 确定dp数组以及下标的含义

dp[i]： 爬到第i层楼梯，有dp[i]种方法

2 . 确定递推公式

如果可以推出dp[i]呢？

从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。

首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。

还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。

使用最小花费爬楼梯

题目

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入： cost = [10,15,20]

输出： 15

解释： 你将从下标为 1 的台阶开始。

• 支付 15 ，向上爬两个台阶，到达楼梯顶部。

总花费为 15 。

示例 2：

输入： cost = [1,100,1,1,1,100,1,1,100,1]

输出： 6

解释： 你将从下标为 0 的台阶开始。

• 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
• 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
• 支付 1 ，向上爬一个台阶，到达楼梯顶部。

总花费为 6 。

提示：

• 2 <= cost.length <= 1000
• 0 <= cost[i] <= 999

代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size() + 1);
        dp[0] = 0; // 默认第一步都是不花费体力的
        dp[1] = 0;
        for (int i = 2; i <= cost.size(); i++) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

题解

1. 确定dp数组以及下标的含义

使用动态规划，就要有一个数组来记录状态，本题只需要一个一维数组dp[i]就可以了。

dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。

对于dp数组的定义，大家一定要清晰！

1. 确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。

dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。

dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。

那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？

一定是选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

1. dp数组如何初始化

看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0] dp[1]推出。

1. 确定遍历顺序

最后一步，递归公式有了，初始化有了，如何遍历呢？

本题的遍历顺序其实比较简单，简单到很多同学都忽略了思考这一步直接就把代码写出来了。

因为是模拟台阶，而且dp[i]由dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组就可以了。

不同路径

题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

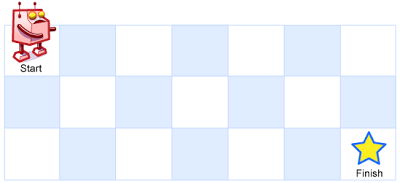
输入： m = 3, n = 7
输出： 28

示例 2：

输入： m = 3, n = 2

输出： 3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入： m = 7, n = 3
输出： 28

示例 4：

输入： m = 3, n = 3
输出： 6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

题解

dfs

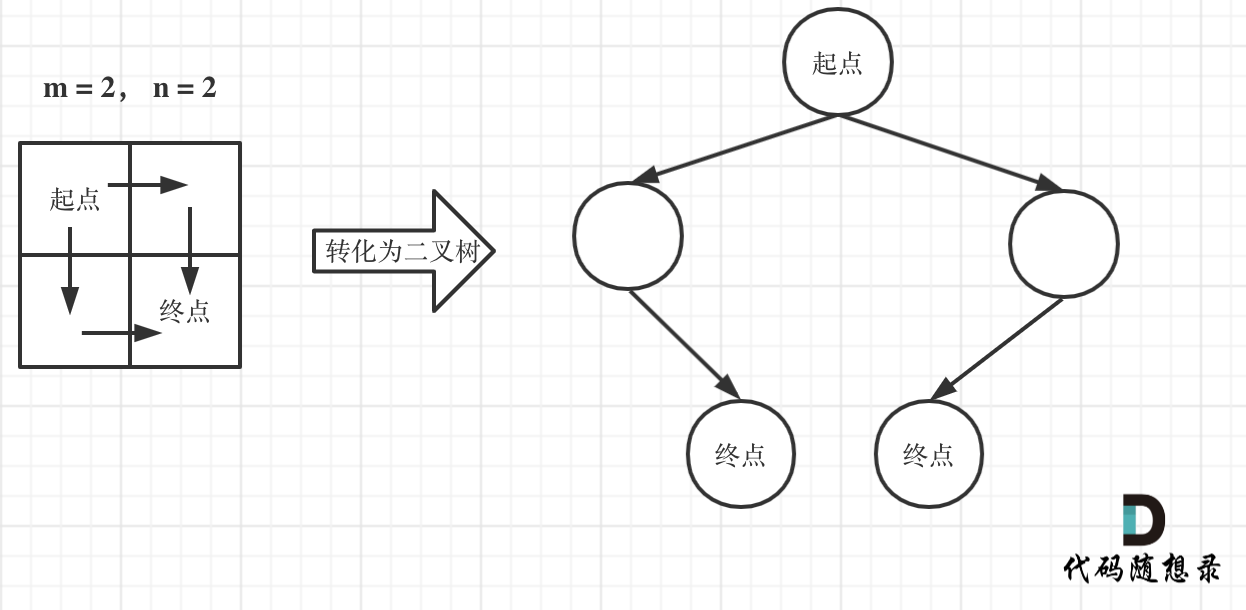
注意题目中说机器人每次只能向下或者向右移动一步，那么其实

机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！

此时问题就可以转化为求二叉树叶子节点的个数

class Solution {
private:
    int dfs(int i, int j, int m, int n) {
        if (i > m || j > n) return 0; // 越界了
        if (i == m && j == n) return 1; // 找到一种方法，相当于找到了叶子节点
        return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
    }
public:
    int uniquePaths(int m, int n) {
        return dfs(1, 1, m, n);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

dp

1. dp数组的定义

   dp[i][j]：表示从(0,0)出发到（i,j）的不同路径

2. 确定递推顺序

   每个位置只有两个方向能走到，dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

3. 数组初始化

   从（0,0）到（i,0）的位置一定只有一种，到（0，j）也同理

   for (int i = 0; i < m; i++) dp[i][0] = 1; for (int j = 0; j < n; j++) dp[0][j] = 1;

4. 确定遍历顺序

   从上方和左边推导过来，只要从左往右一层一层遍历即可。

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int j = 0; j < n; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

凑硬币

题目

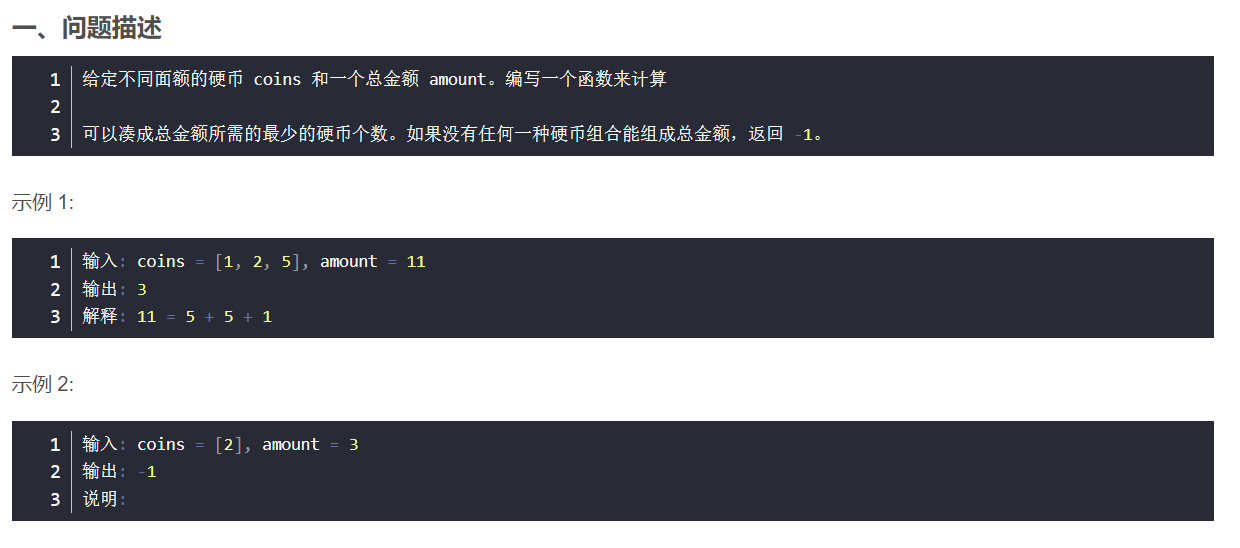
题解

dfs

#include<bits/stdc++.h>
using namespace std;
/*
coins：硬币的面额列表；
amount：需要凑的金额；
count：当前使用硬币的数量；
index：当前搜索的硬币面额的下标；
res：存储最少的硬币数量。
*/
void dfs(vector<int>& coins, int amount, int count, int index, int& res) {
    if (amount == 0) {
        res = min(res, count);
        return;
    }
    if (index == coins.size()) {
        return;
    }
    for (int k = amount / coins[index]; k >= 0 && count + k < res; k--) {
        dfs(coins, amount - k * coins[index], count + k, index + 1, res);
    }
}

int coinChange(vector<int>& coins, int amount) {
    sort(coins.rbegin(), coins.rend());
    int res = INT_MAX;
    dfs(coins, amount, 0, 0, res);
    return (res == INT_MAX ? -1 : res);
}

int main() {
    vector<int> coins = {1, 2, 5};
    int amount;
    cin>>amount;
    int res = coinChange(coins, amount);
    cout << res << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

dp

#include<bits/stdc++.h>
using namespace std;
int amount;
vector<int> coins={1,2,5};


int main()
{
    cin>>amount;
    vector<int> dp(amount+1,amount+1);//初始值也为amount + 1,是取不到的
    dp[0]=0;
    for(int i=0;i<dp.size();i++)
    {
        for(auto e:coins)
        {
            if(i-e<0) continue;
            dp[i]=min(dp[i],dp[i-e]+1);
        }
    }
    
    if(dp[amount]==amount+1) cout<<-1<<endl;
    else cout<<dp[amount];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

dp数组定义：凑其前i金额需要的硬币数量。

初始值也为amount + 1,是取不到的

base case：自底向上思考，dp[0]为0：金额为0时就不再需要硬币了

选择：从硬币面值组合里面选

状态：假设前i-1个已经选完了，最后选一个正好凑完

状态转移： dp[i]=min(dp[i],dp[i-e]+1);需要判断i-e是否>0

滑雪

题目

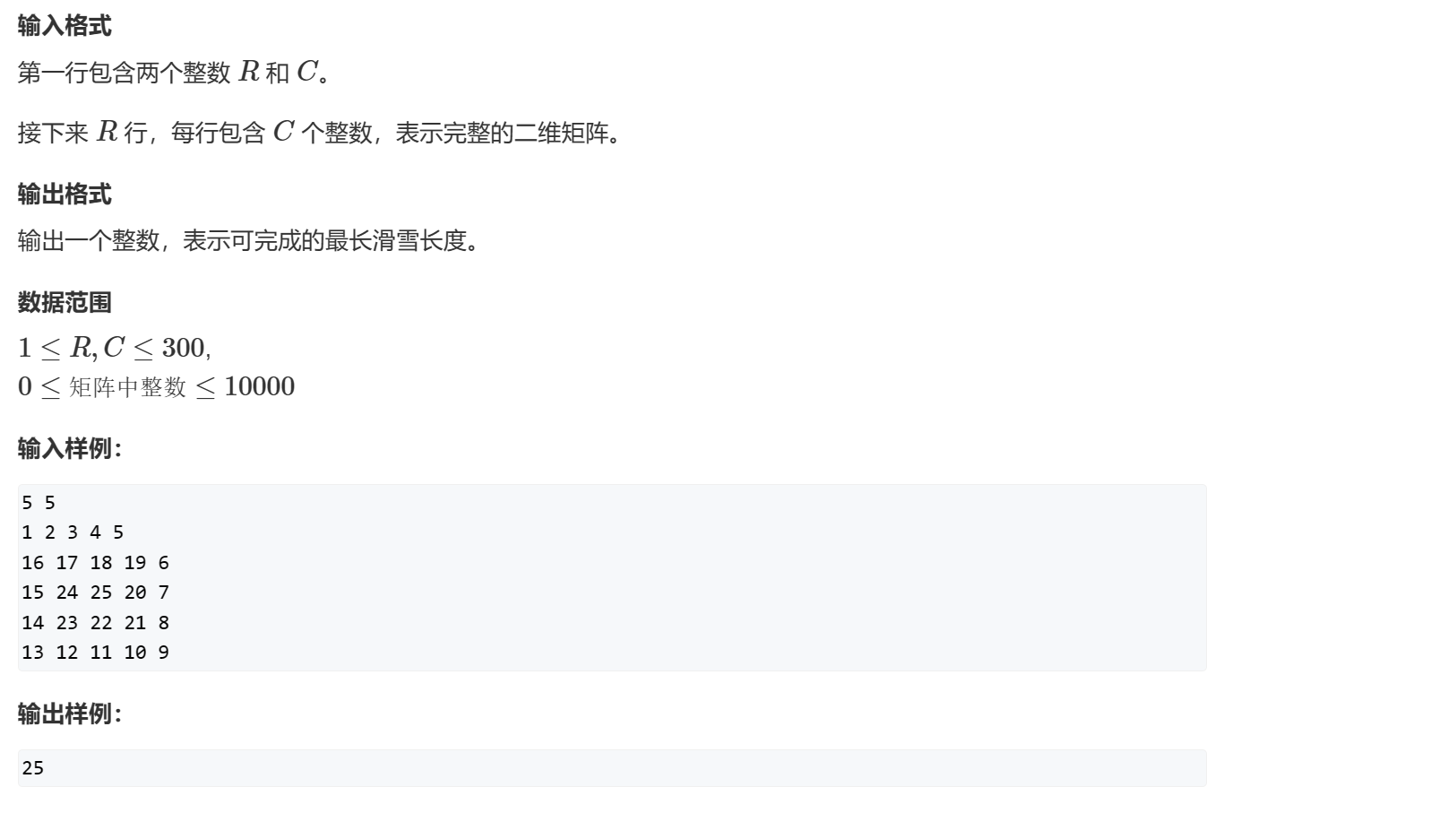
代码

#include<bits/stdc++.h>
using namespace std;
const int N=310;
int n,m;
int g[N][N];//不能存在有环图
int f[N][N];//所有从i,j开始滑的路径，属性是max
//集合分为四类，向上向右向左向下
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};

int dp(int x,int y)
{
    int &v=f[x][y];//引用即为取别名
    if(v!=-1) return v;//表示已经算过了
    v=1;//最小值为1
    for(int i=0;i<4;i++)
    {
        int a=x+dx[i],b=y+dy[i];
        if(a>=1&&a<=n&&b>=1&&b<=m&&g[x][y]>g[a][b])
        v=max(v,dp(a,b)+1);
    }
    return v;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>g[i][j];
            
    memset(f,-1,sizeof f);//初始化表示每个路径都没被算过
    int res=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            res=max(res,dp(i,j));
    cout<<res<<endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

题解

本题考察使用记忆化搜索优化dp的算法

思路是：枚举路径上的每一个点，找到最大值，而每一个点又能分为四种小的递推的状态，因此可以使用动态规划来解决。

dp数组：使用一个二维数组来表示路径的长度

属性：最大值，满足条件即更新

记忆化搜索技巧：初始化数组表示没有被算过，如果已经被计算过就可以直接返回

汉罗塔

题目

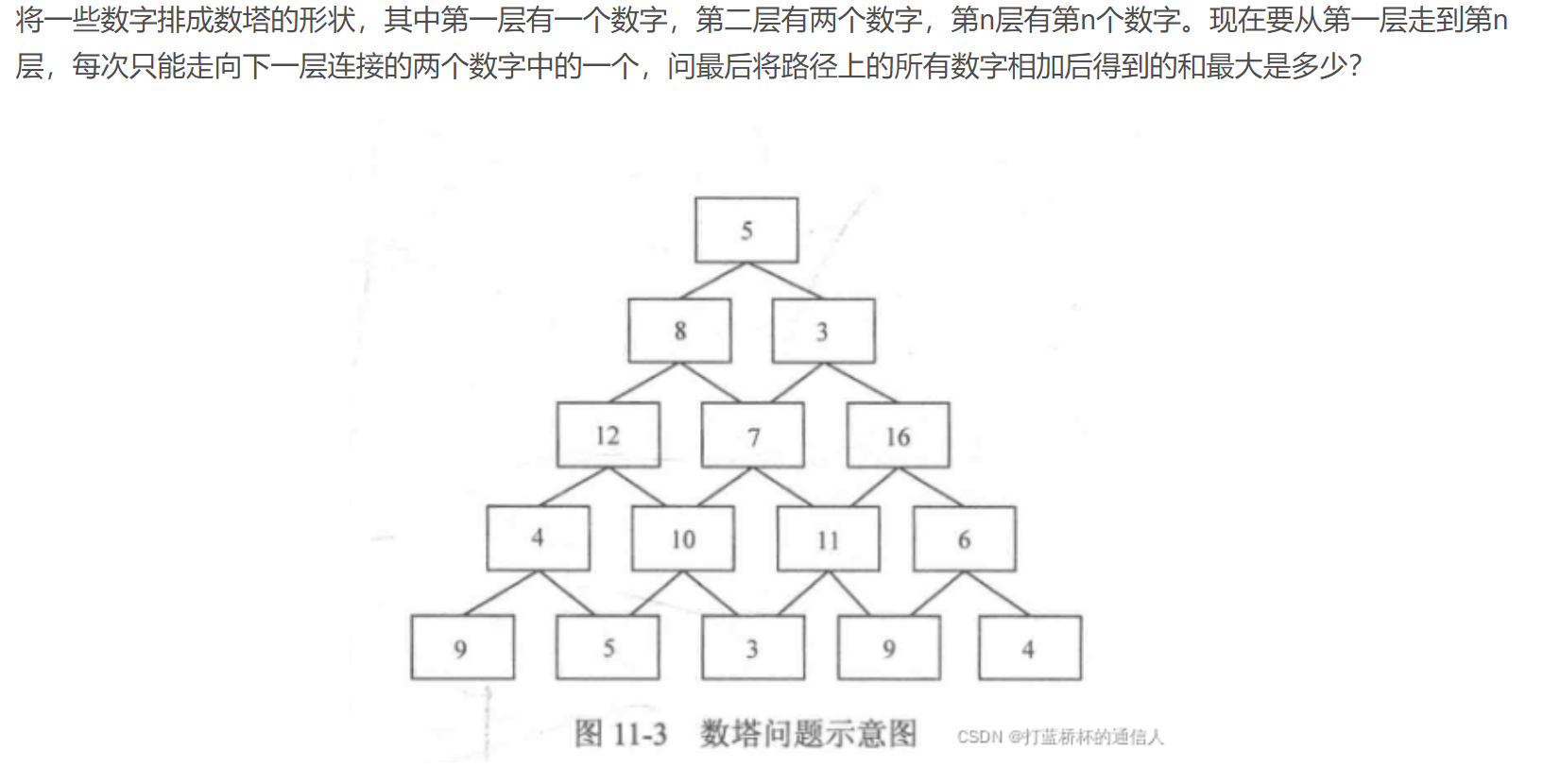
题解

dfs

可以用dfs来搜索所有的情况取最大值

参数：

1. index表示到第几层
2. y表示枚举该层的第一个还是第二个数
3. sum表示总和

#include<bits/stdc++.h>
using namespace std;

const int N=10;
int f[N][N];

int ans;
int n;
void dfs(int index,int y,int sum)
{
    if(index==n)
    {
        ans=max(ans,sum);
        return ;
    }
    
    dfs(index+1,y,sum+f[index+1][y]);
    dfs(index+1,y+1,sum+f[index+1][y+1]);
}


int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<=i;j++)
        {
            cin>>f[i][j];
        }
        
    dfs(0,0,f[0][0]);
    cout<<ans<<endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

dp

#include<bits/stdc++.h>
using namespace std;

const int N=10;
int f[N][N];
int dp[N][N];//表示从i,j到最后一层路径中的最大数字之和
int n;

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<=i;j++)
        {
            cin>>f[i][j];
        }
        
    for(int i=0;i<n;i++)
    {
        dp[n-1][i]=f[n-1][i];//处理边界
    }
    
    //从后往前枚举
    for(int i=n-2;i>=0;i--)
    {
        for(int j=0;j<=i;j++)
        {
            dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j];//递推式
        }
    }
    cout<<dp[0][0]<<endl;
    

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

注意本题是从后往前枚举，根据dp数组的定义从i,j到最后一层路径中的最大数字之和，也就是要输出

dp[0][0]

01背包问题

题目

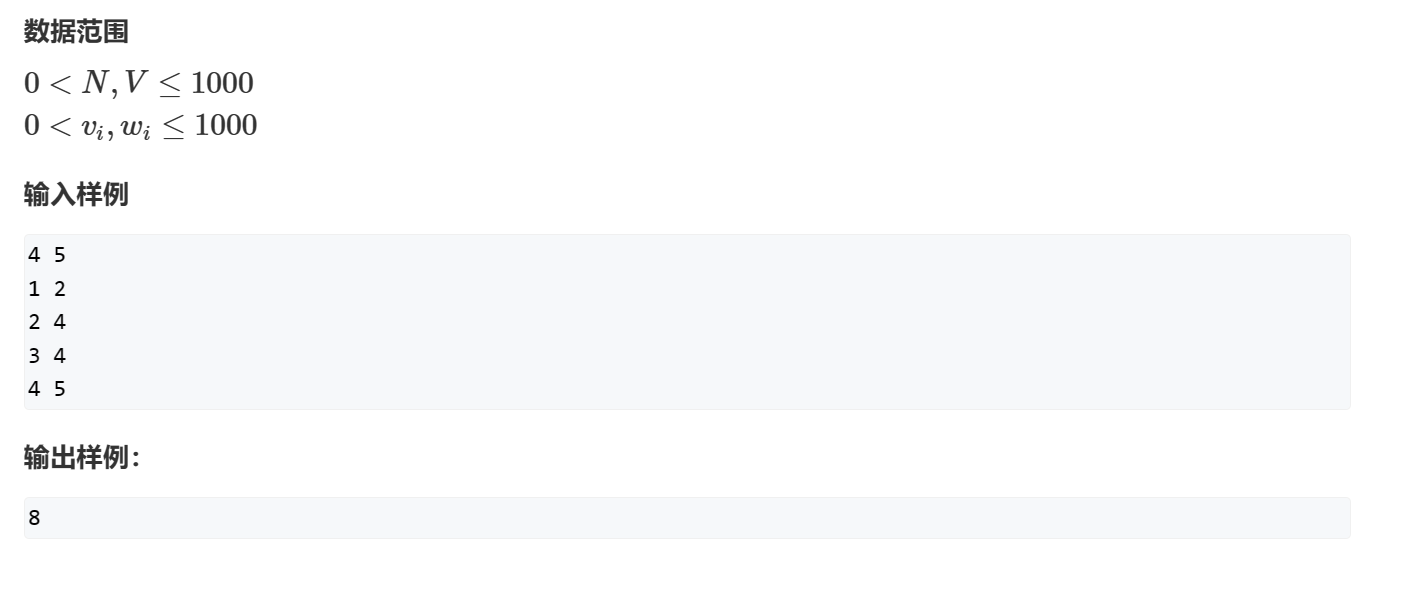
代码

#include<bits/stdc++.h>
using namespace std;

const int N=10010;
int n,V;
int v[N],w[N];
int f[N][N];//从i个物品中选，体积不超过j

int main()
{
    cin>>n>>V;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i];
        
    for(int i=1;i<=n;i++)
        for(int j=1;j<=V;j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j<v[i]) f[i][j]=f[i-1][j];
               // 能装，需进行决策是否选择第i个物品
            else{
                f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
            }
        }
        
    cout<<f[n][V]<<endl;
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

题解

摘花生

题目

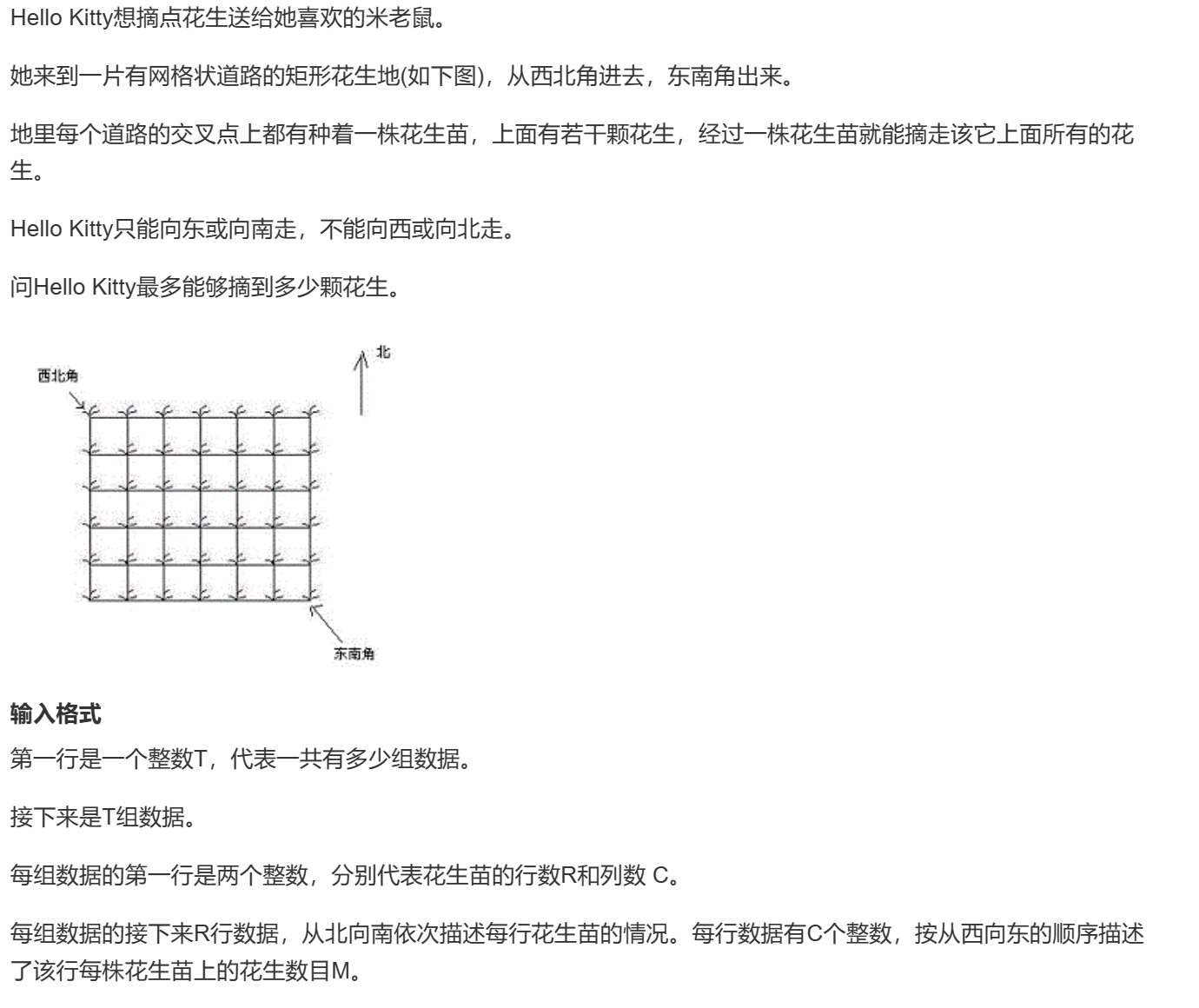
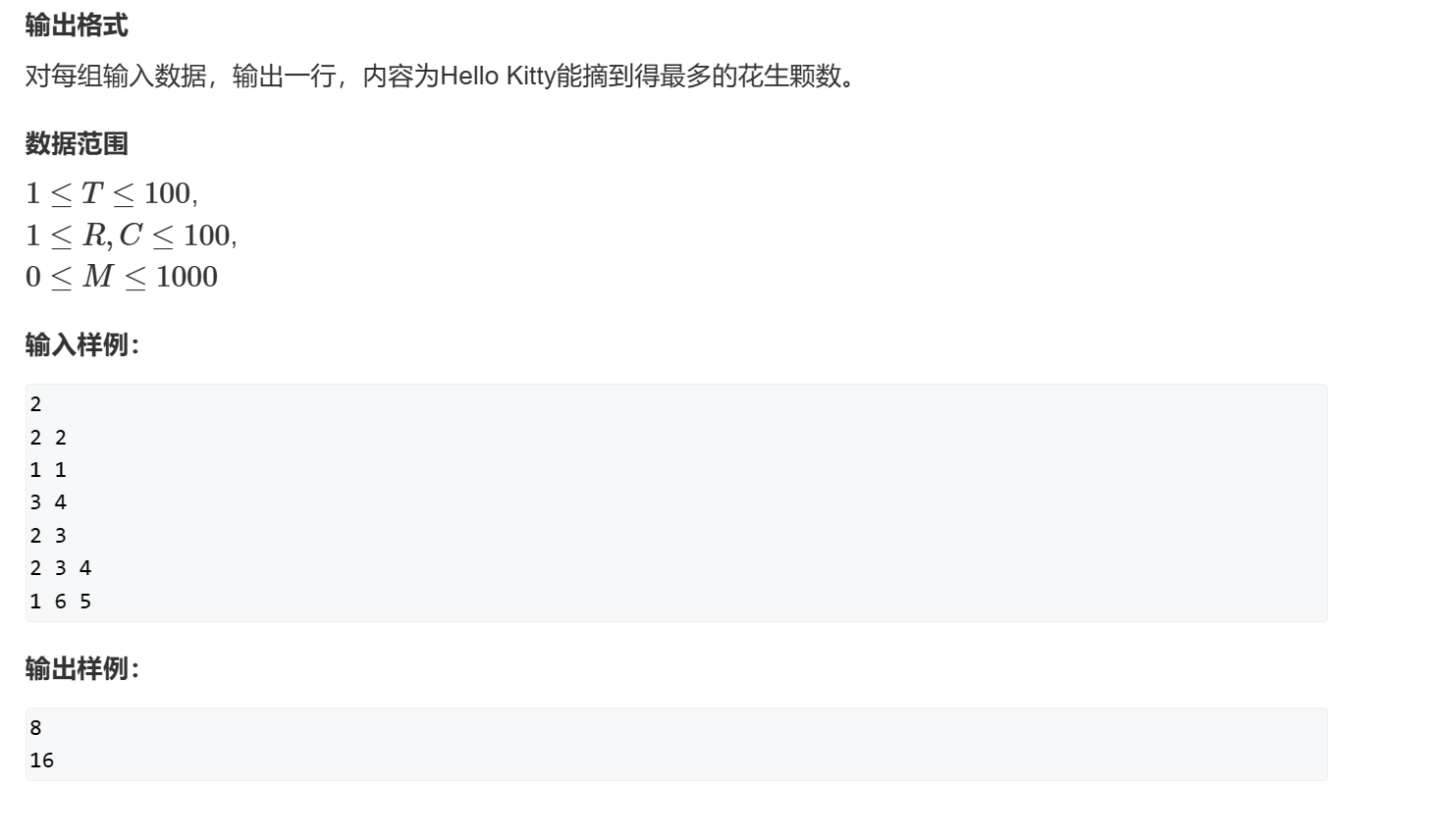
代码

#include<bits/stdc++.h>
using namespace std;

const int N=110;
int a[N][N];
int dp[N][N];//从(1,1)到(i,j)所有路径中能摘得花生最多的路径
int t;
int n,m;
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                cin>>a[i][j];
                
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                dp[i][j]=max(dp[i-1][j]+a[i][j],dp[i][j-1]+a[i][j]);
                
                
        cout<<dp[n][m]<<endl;
    }
    

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

题解

用闫式dp法来分析：

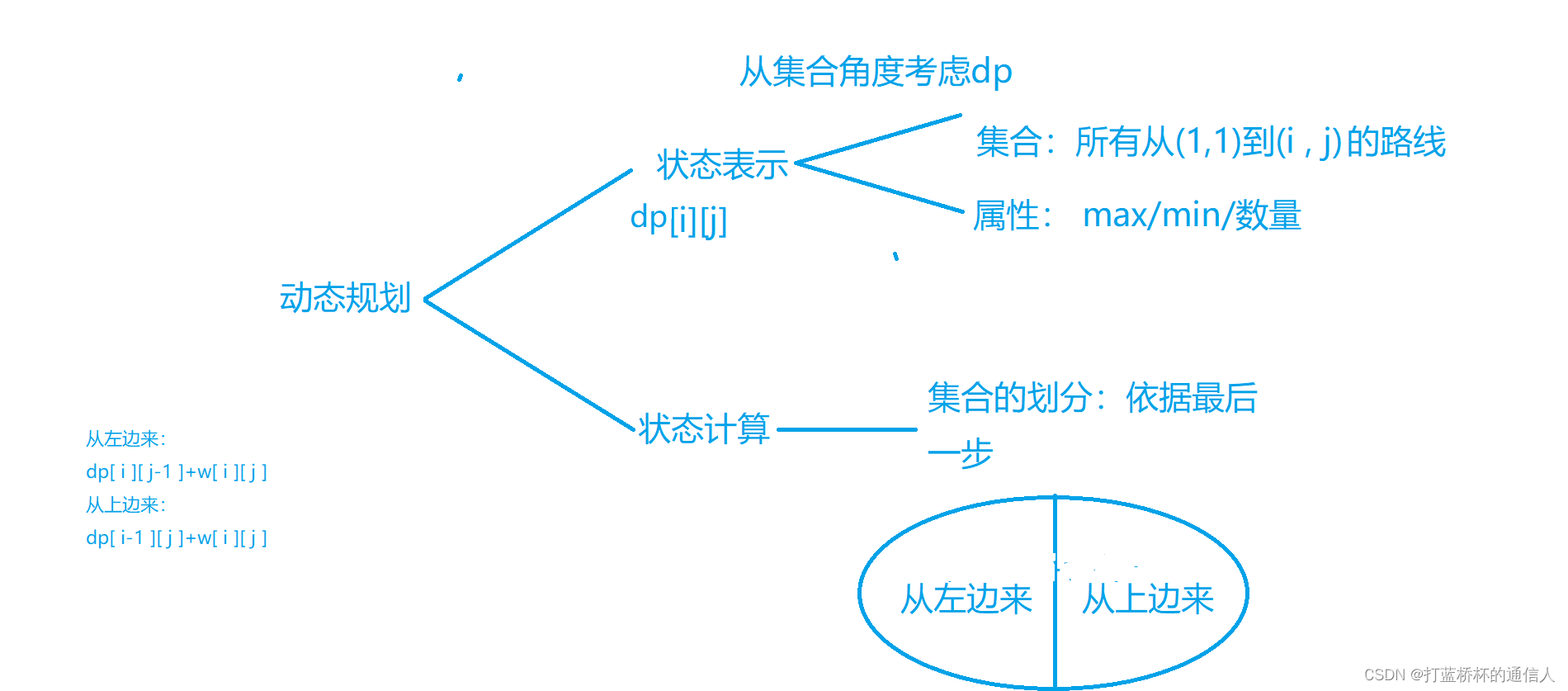
最长上升子序列

题目

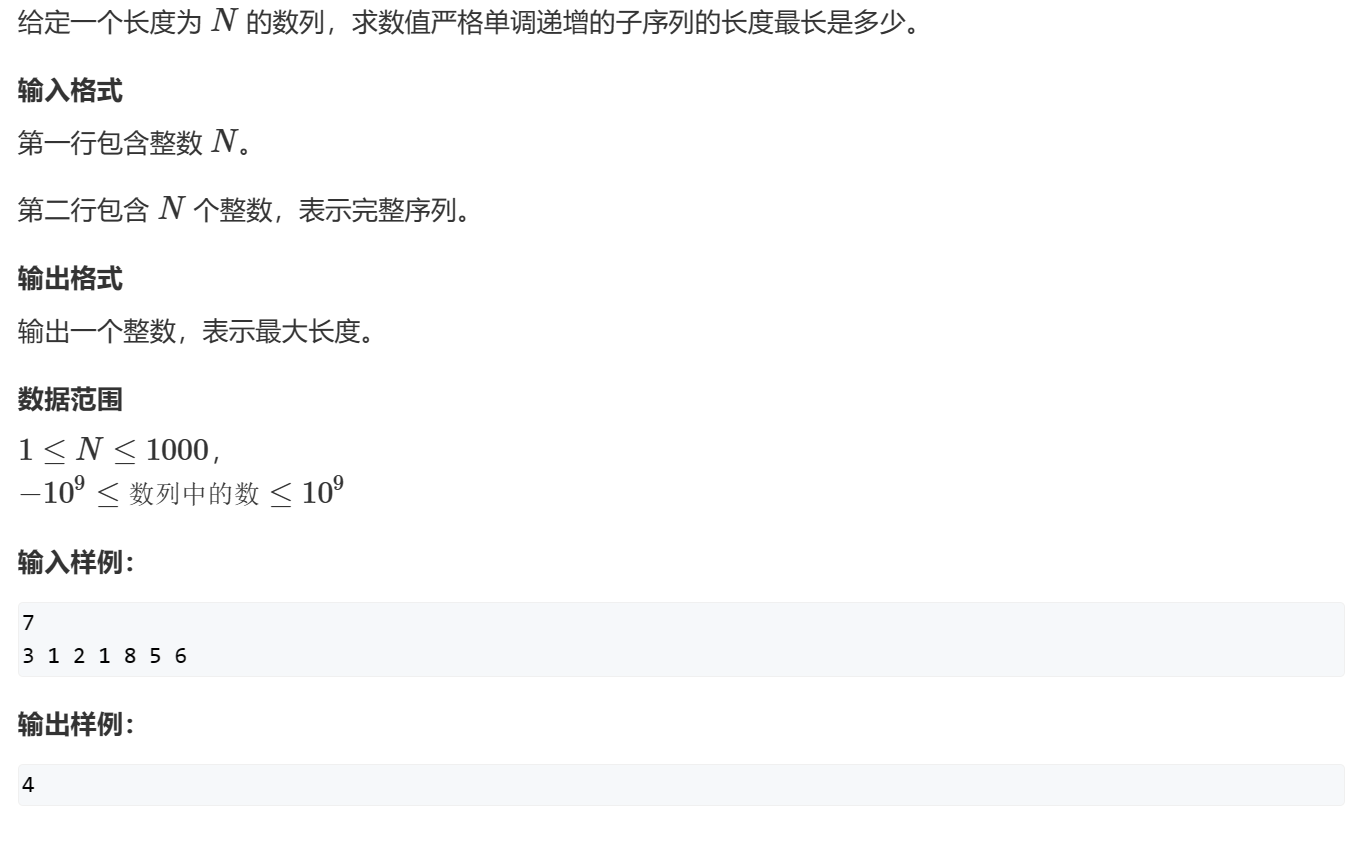
代码

#include<bits/stdc++.h>
using namespace std;
const int N=1010;

int a[N];
int dp[N];//表示以i结尾的最长上升子序列
int  n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
        
    for(int i=1;i<=n;i++)
        dp[i]=1;
        
    for(int i=1;i<=n;i++)
        for(int j=1;j<i;j++)
        {
            if(a[i]>a[j])
            dp[i]=max(dp[i],dp[j]+1);
        }
        
    int res=0;
    for(int i=1;i<=n;i++)
        res=max(res,dp[i]);
        
    cout<<res<<endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

题解

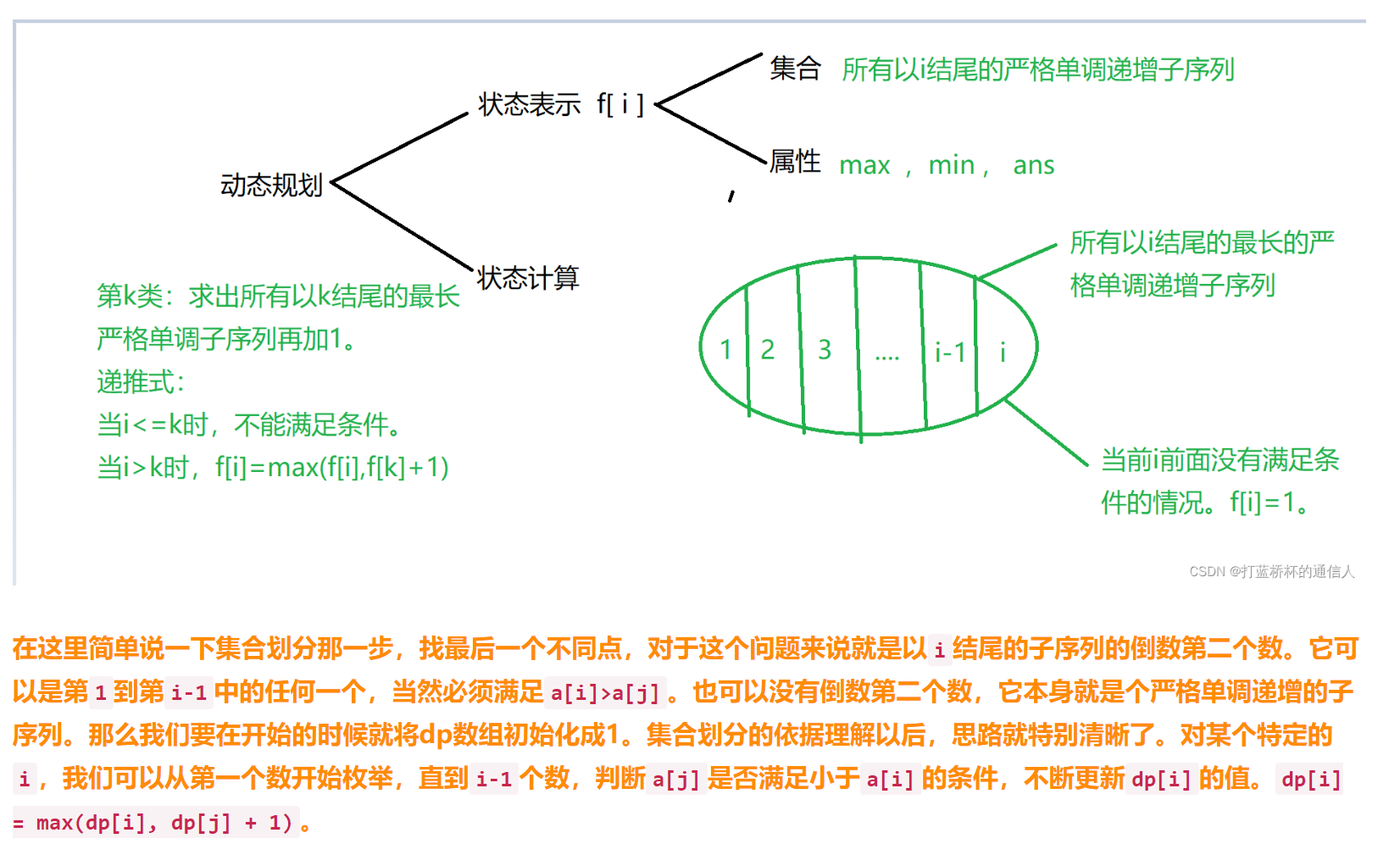
总结

动态规划是一种非常重要的算法思想，它可以解决很多实际问题，并且在计算机科学领域中有着广泛的应用。通过本博客的学习，我们可以了解到动态规划的基本概念、算法原理和应用场景。

在实际应用中，动态规划算法可以用于解决很多优化问题，如背包问题、最长公共子序列问题、最短路径问题等。学习动态规划算法不仅可以提高算法设计和解决问题的能力，还可以帮助我们更好地理解计算机科学中的一些基本概念和方法。

总之，动态规划算法是一种非常重要的算法思想，需要我们不断地学习和实践，才能更好地掌握它的精髓，并将其应用到实际问题中。希望本博客能够为读者提供一些启示和帮助，促进大家在算法学习和实践中的进步和成长。也祝大家考出好成绩！！