图神经网络基础_自定义节点嵌入gnn

1 回顾

1.1 节点嵌入

传统机器学习难以应用在图结构上。节点嵌入是将节点映射到d维向量，使得在图中相似的节点在向量域中也相似。存在以下问题：

• 复杂度高，每个节点的嵌入向量都需要单独训练
• 无法获取在训练时没出现过节点的表示向量，无法泛化到新图或新节点
• 无法应用节点自身属性特征信息

1.2 GNN结构

deep graph encoders：即用GNN进行节点嵌入

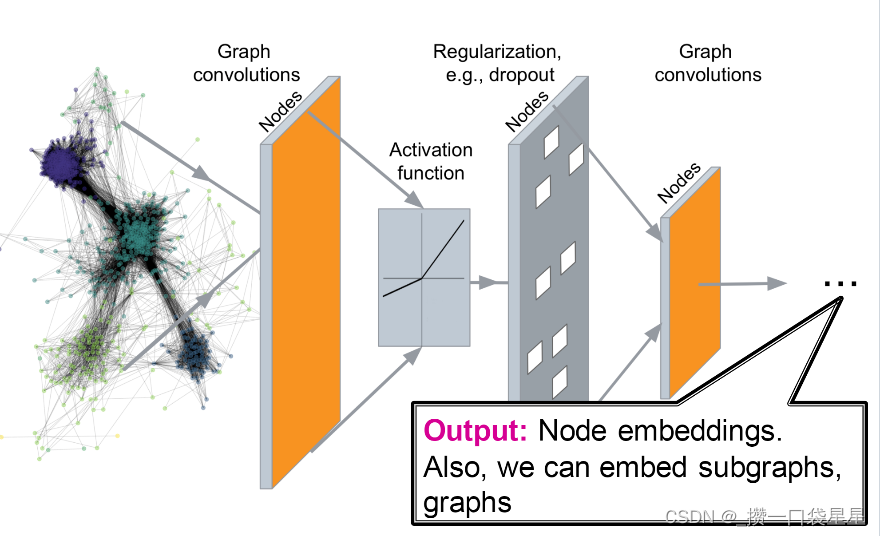
1.3 任务

• 节点分类：预测节点的标签
• 链接预测：预测两点是否相连
• 社区发现：识别密集链接的节点簇
• 网络相似性：度量图/子图间的相似性

2 图深度学习

Assume:
图 G
节点集 V
邻接矩阵 A（二元，无向无权图。这些内容都可以泛化到其他情况下）
节点特征矩阵 X
一个节点 v
v 的邻居集合N(v)
如果数据集中没有节点特征，可以用指示向量indicator vectors（节点的独热编码），或者所有元素为常数1的向量。有时也会用节点度数来作为特征。

2.1 DNN

将邻接矩阵拼和节点特征合并，用DNN训练，缺点：

• 参数多
• 如果图发生变化，邻接矩阵发生变化，无法适配原DNN（我理解是，只能用于原图）
• DNN对输入顺序比较敏感，而图是无序的，相同图不同的顺序图的邻接矩阵不一样，DNN无法处理无序的结构（我们需要一个即使改变了节点顺序，结果也不会变的模型）

---->借用CNN的思想，将网格上的卷积神经网络泛化到图上，并应用到节点特征数据。但是在CNN中，卷积核大小是固定的，而图的邻居无法用固定大小的卷积核来处理（图上无法定义固定的lacality或滑动窗口且节点顺序不固定），因此用的是聚合（aggregation） 思想。

2.2 聚合思想

1.转换邻居信息，将其加总

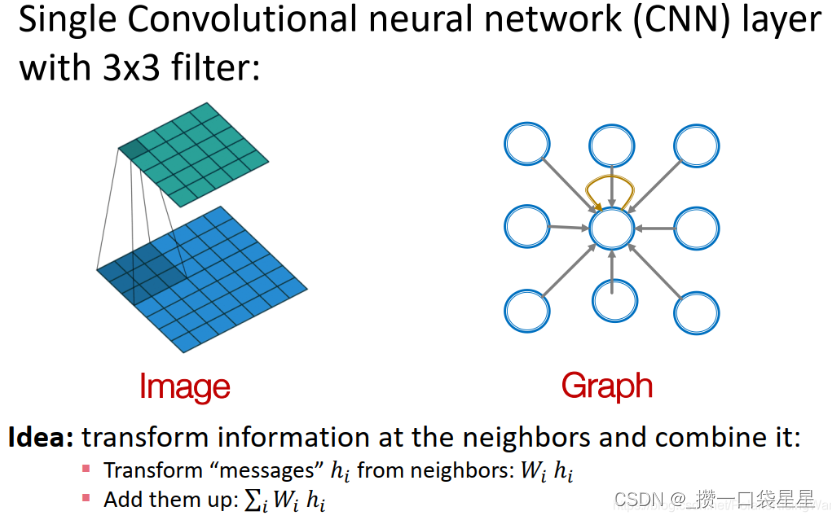
2. Graph Convolutional Networks
通过节点邻居定义其计算图，传播并转换信息，计算出节点表示（可以说是用邻居信息来表示一个节点）

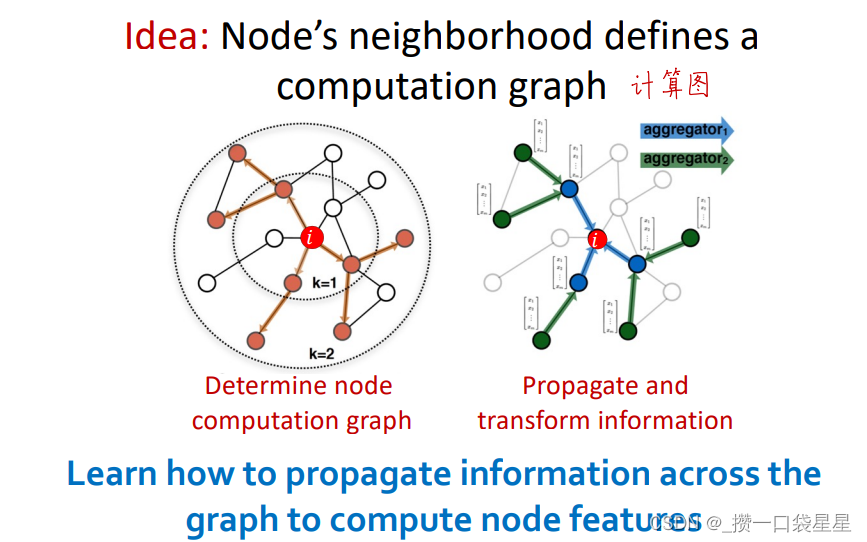
3.核心思想：通过聚合邻居来生成节点嵌入
通过神经网络聚合邻居信息，通过节点邻居定义计算图（它的邻居是子节点，子节点的邻居又是子节点们的子节点……）

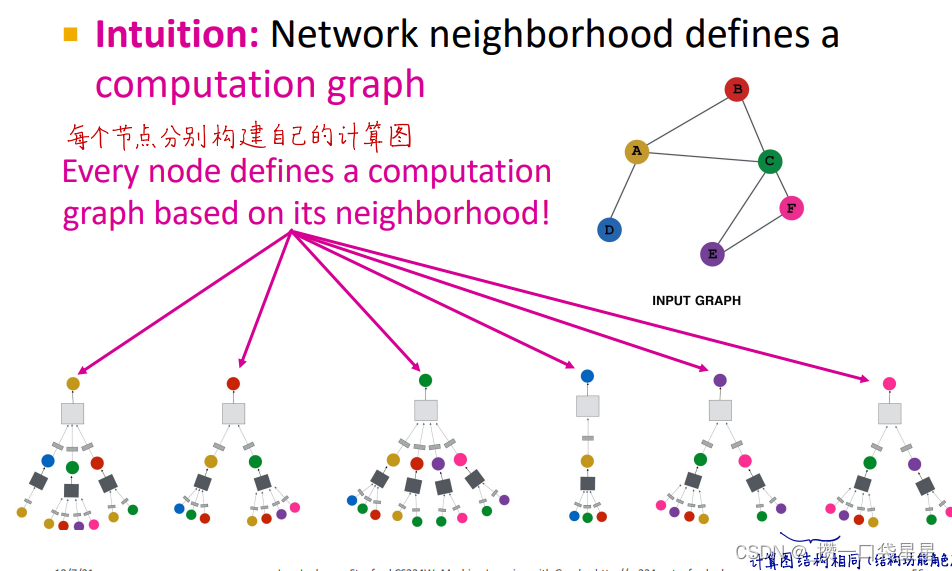
4.深度模型：很多层
节点在每一层都有不同的表示向量，每一层节点嵌入是邻居上一层节点嵌入再加上它自己（相当于添加了自环）的聚合。
第0层是节点特征，第k层是节点通过聚合k hop邻居所形成的表示向量。
图神经网络的层数是计算图的层数，而不是神经网络的层数。根据六度空间理论，这个层数没必要太大
在这里就没有收敛的概念了，直接选择跑有限步（k）层。

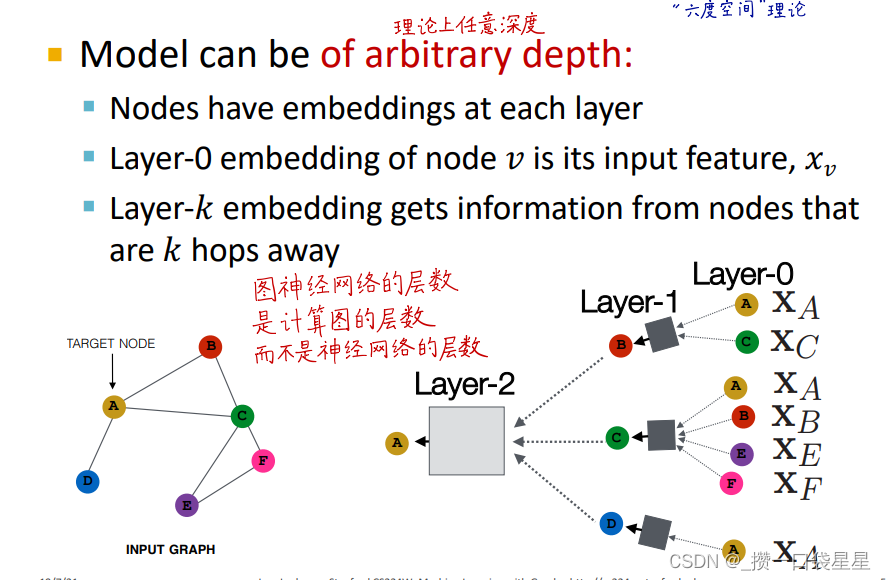
5.邻居信息聚合neighborhood aggregation
盒子里就是一个全连接神经网络
不同聚合方法的区别就在于如何跨层聚合邻居节点信息。neighborhood aggregation方法必须要order invariant或者说permutation invariant
基础方法：从邻居获取信息求平均，再应用神经网络


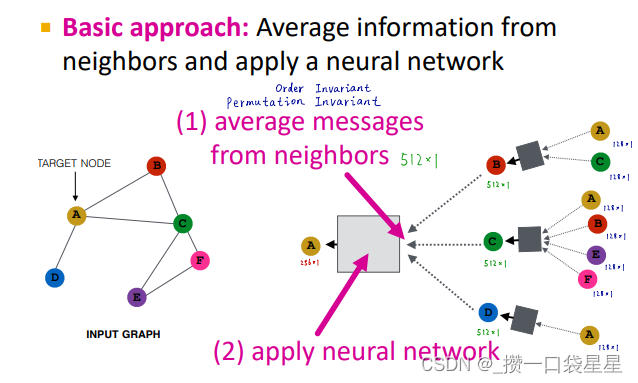
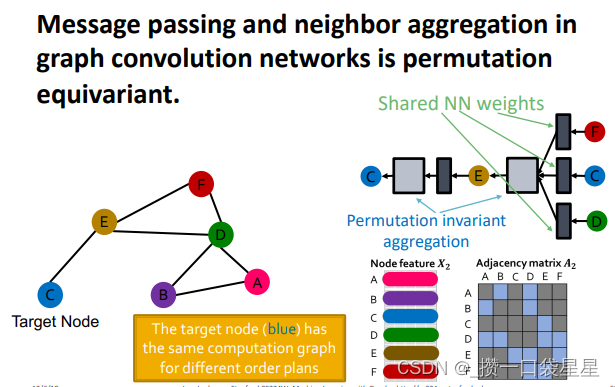
不同顺序下，目标节点有相同的计算图

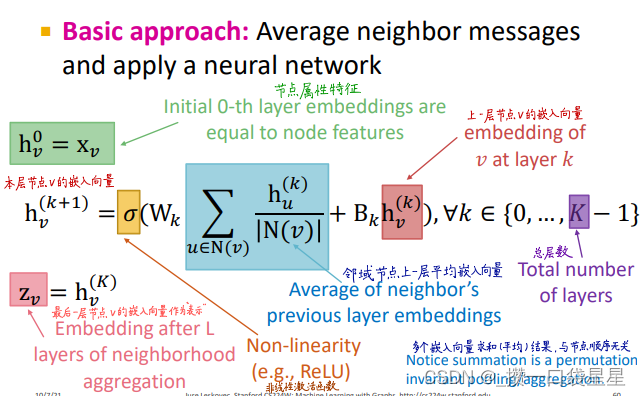
2.3 模型训练

模型上可以学习的参数有Wl（neighborhood aggregation的权重）和Bl转换节点自身隐藏向量的权重）（注意，每层参数在不同节点之间是共享的）。
可以通过将输出的节点表示向量输入损失函数中，运行SGD来训练参数。

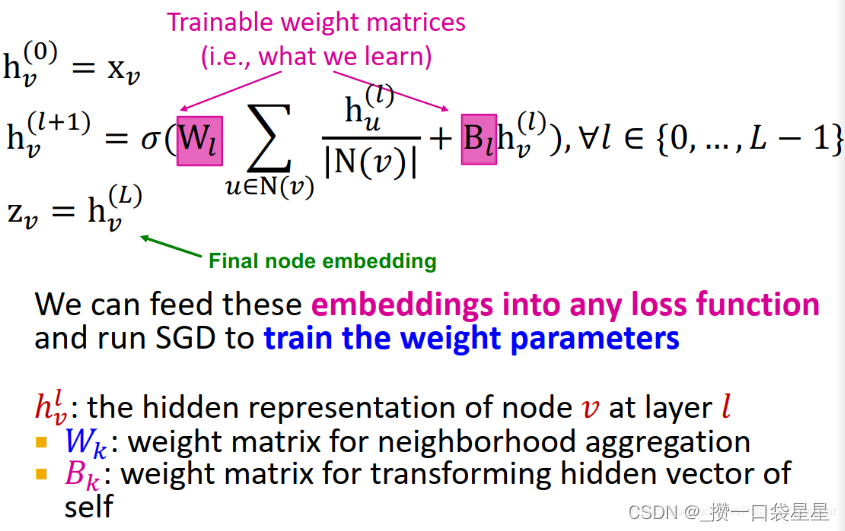
矩阵形式


训练：监督学习和非监督学习
非监督学习

监督学习

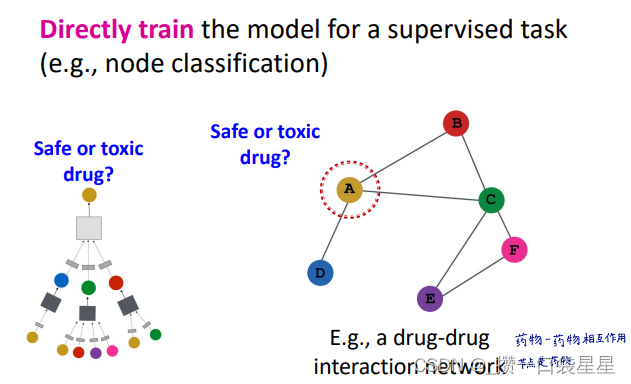
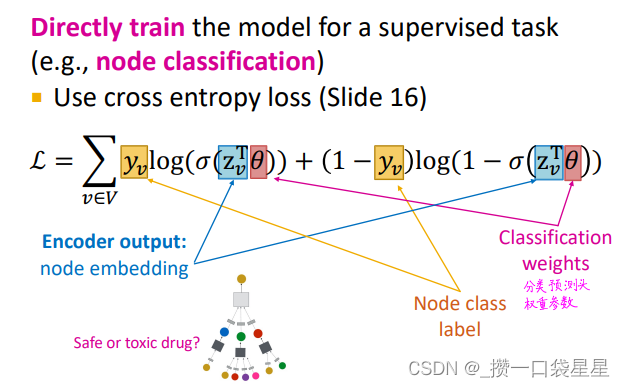
2.4 模型设计概述

第一步：定义节点聚合的函数
第二步：定义节点嵌入的损失函数
第三步：训练
第四步：生成节点嵌入
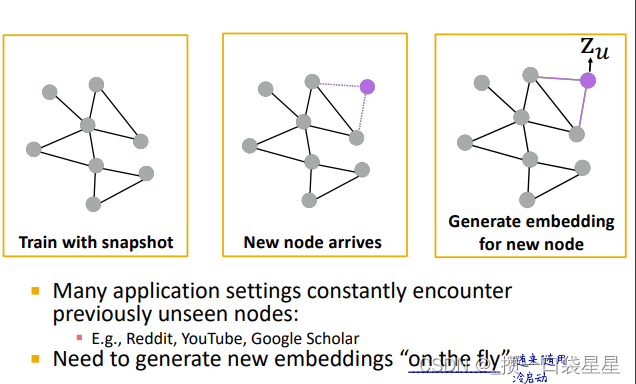
第五步：泛化到新节点



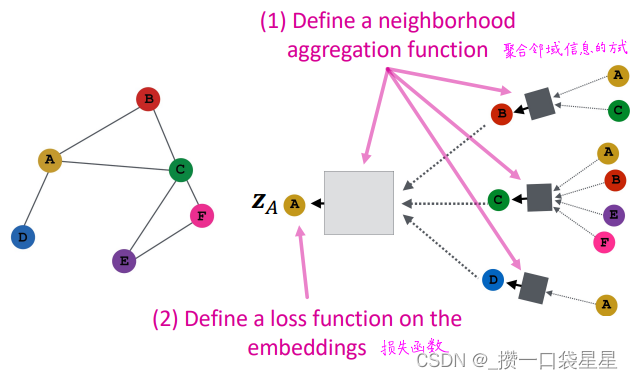
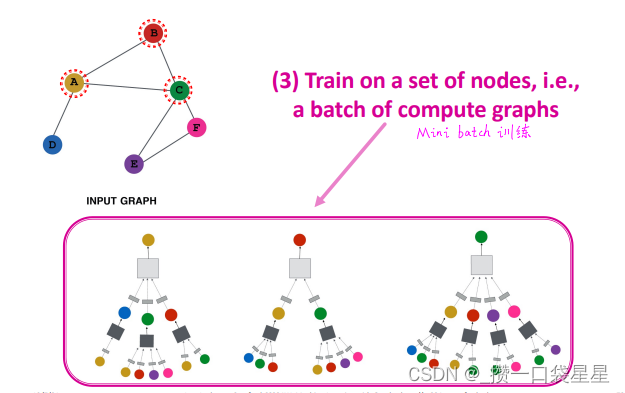
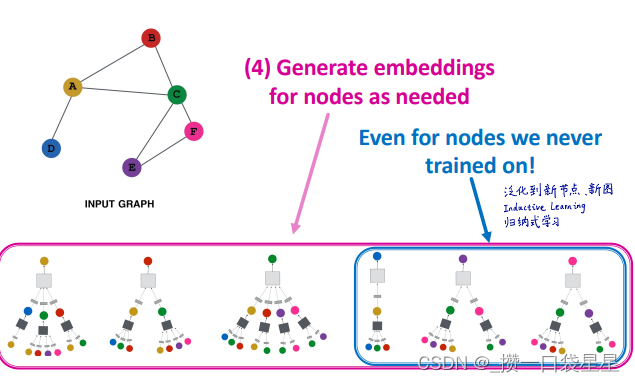
泛化到新节点：聚合参数在所有节点共享---->泛化到新图

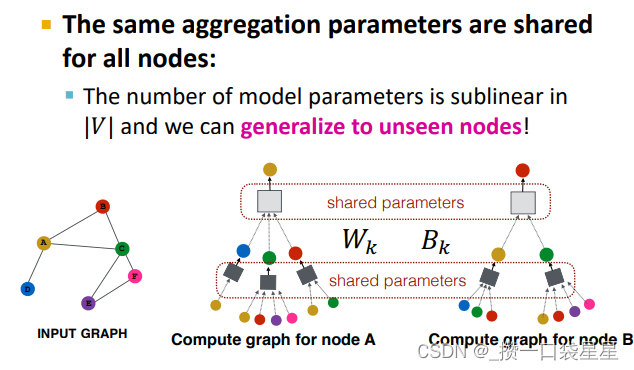
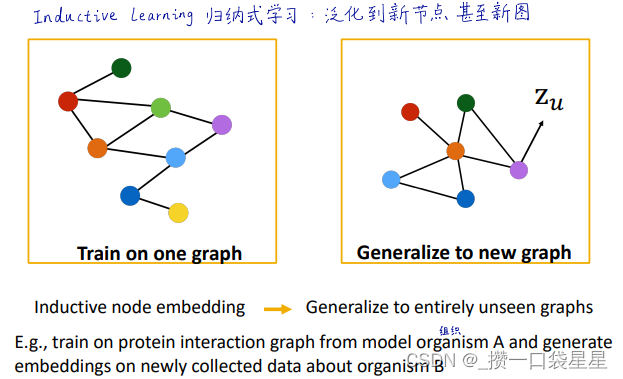
2.5 GNN vs CNN

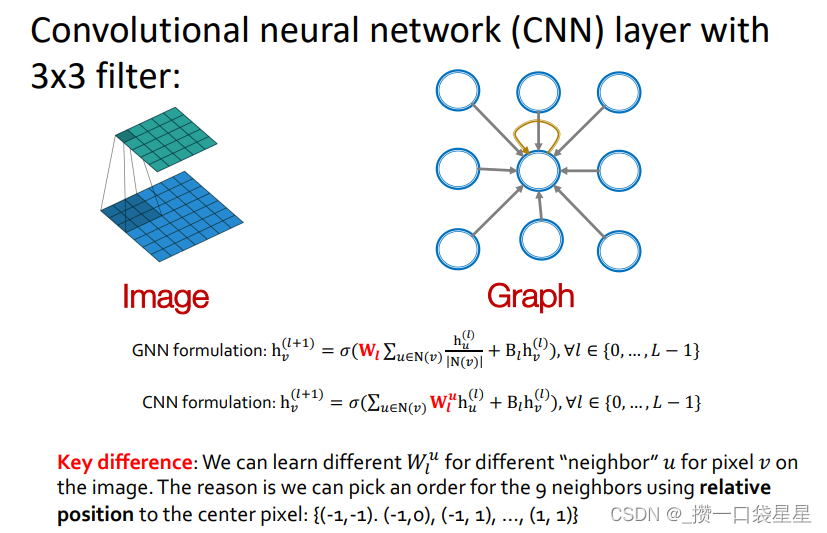
CNN可以看作时一个有固定邻域和固定顺序特殊的GNN

• CNN卷积核尺寸是预先定义的
• GNN的优势在于可以处理任意一个节点度不同的图
• CNN不是顺序不变的，改变像素的顺序可以得到不同的输出

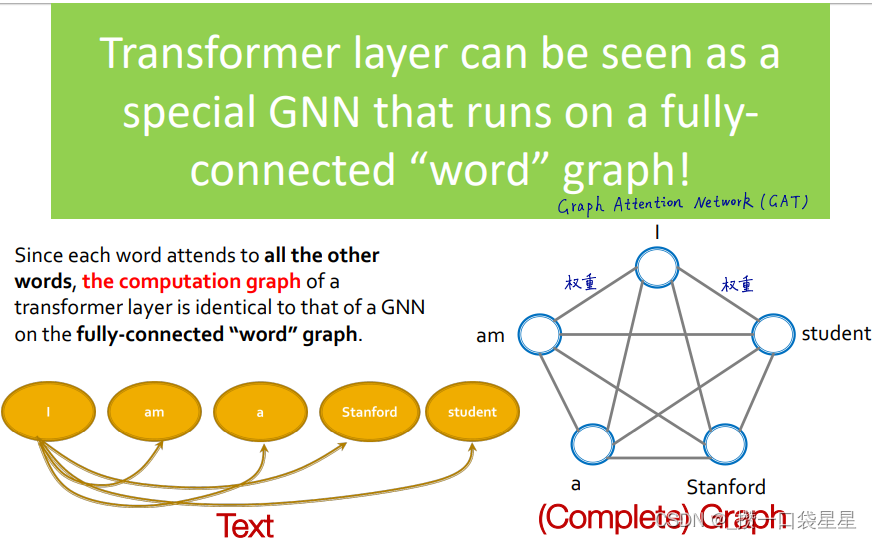
2.6 GNN transformer

transformer:处理顺序问题，核心是自注意力

• transformer可以看作是一个全连接词图的特殊GNN

3 图神经网络

优点

1. 深度学习拟合学习能力强
2. 归纳式学习可以泛化到新节点新图
3. 参数量少、所有计算图共享神经网络
4. 利用节点的属性特征
5. 利用节点的标注类别
6. 区分节点结构功能角色（桥接、中枢、外围区域）
7. 只需寥寥基层就可以让任意两个节点相互影响

3.1 GNN 基础

3.1.1 框架

• 原始输入图=!计算图（特征扩增和结构扩增）
• GNN layer：邻域信息转换+邻域信息聚合
• layer connectivity:按顺序堆叠
• 训练：监督或半监督
• 训练目标：节点、边、图
  

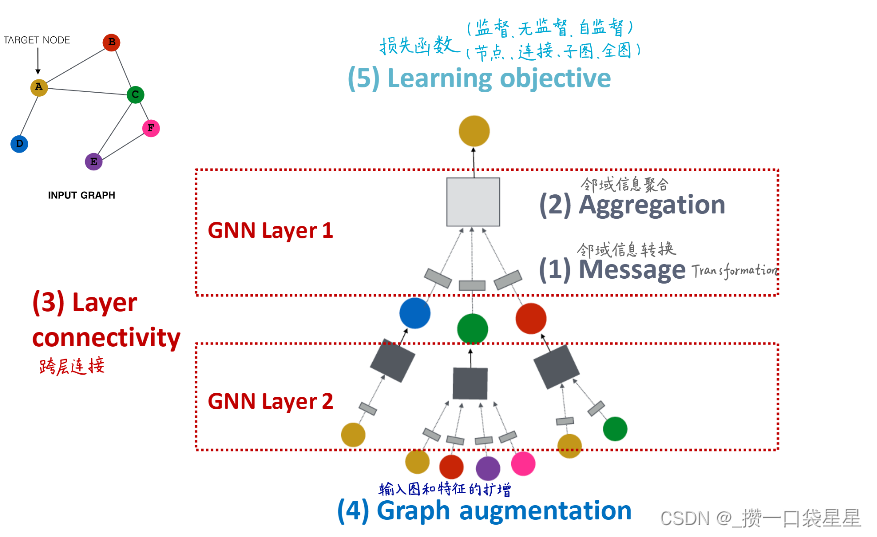
3.1.2 GNN layer=邻域信息转换+邻域信息聚合

1. 有多种例子，GCN/ GraphSAGE/GAT

• 把多个邻居节点和自己的向量转换成一个向量
• 邻居节点的向量集合与节点顺序无关

2. 邻域信息转换
   
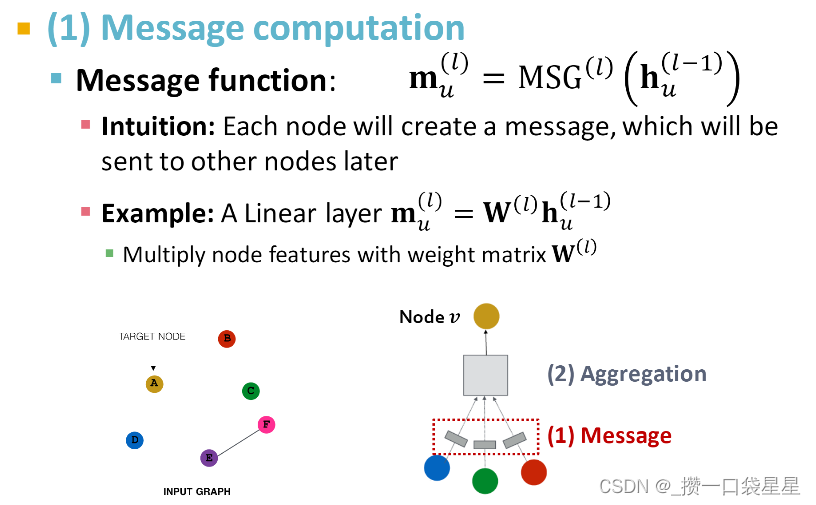
3. 邻域信息聚合
   聚合方法可以是求和、平均、最大
   
4. 存在问题
   如果只用邻居节点的信息，说明该节点只取决于邻居节点---->解决办法：加上自己的节点信息
   
5. GNN layer
   
6. Classical GNN layer (GCN)
   
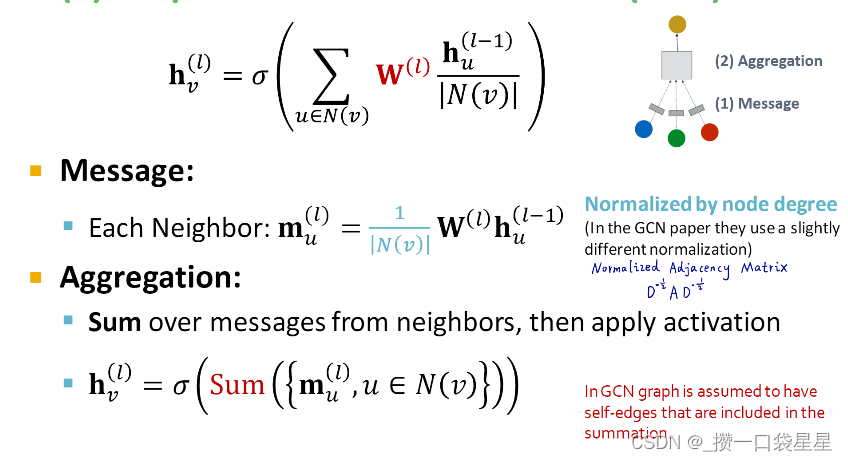
7. GraphSAGE
   个人理解是用到了邻域信息和自己的信息
   
   AGG的方法有
   
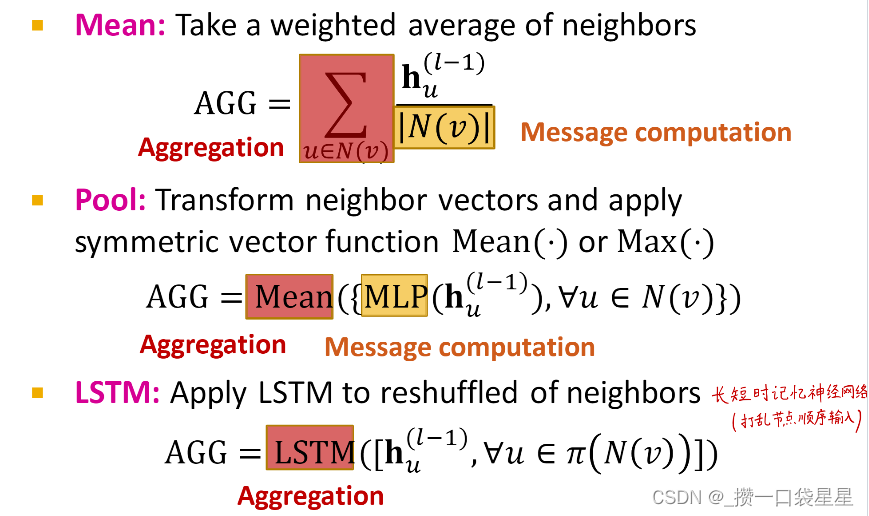
   l2归一化
   
8. GAT graph attention networks
   在 GCN和GraphSAGE中，邻居节点对该节点的权重系数取决于图的连接结构（节点度），且不同邻居带来的信息权重相同
   —>实际上，不同节点带来的权重是不同的，引入注意力权重
   第一步：用自注意力函数对每个邻居节点计算一个注意力分数
   
   第二步：自注意力函数

• 自注意力系数是一个标量
• 自注意力函数自定义，可以是一个单层神经网络
  
  第三步：用softmax 将自注意力系数归一化为权重，最后加权求和得到聚合结果
  注意力机制改进—多头注意力机制：避免偏见，陷入局部最优
  分别训练不同的自注意力函数，每个函数对应一套自注意力权重
  
  自注意力机制的优点：
• 不同节点权重不同
• 计算高效：可以并行计算
• 存储高效
• 局部图参与计算
• 泛化
  

3.1.3 GNN layer in practice

1. 框架
   
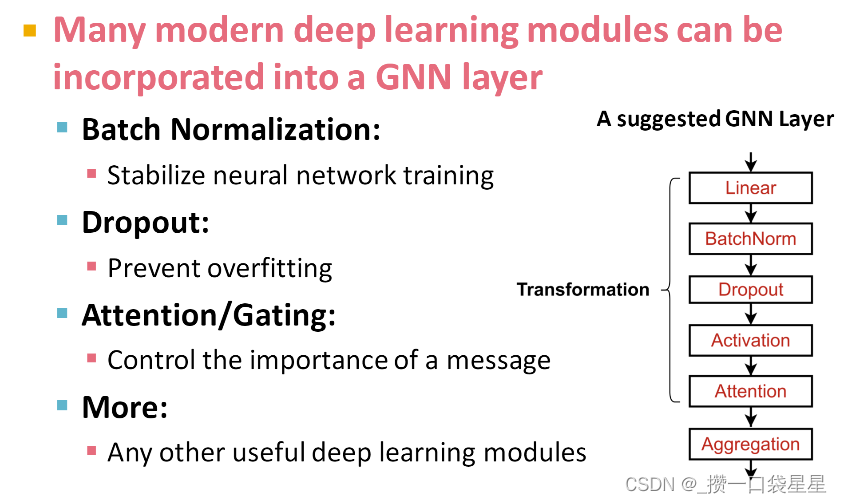
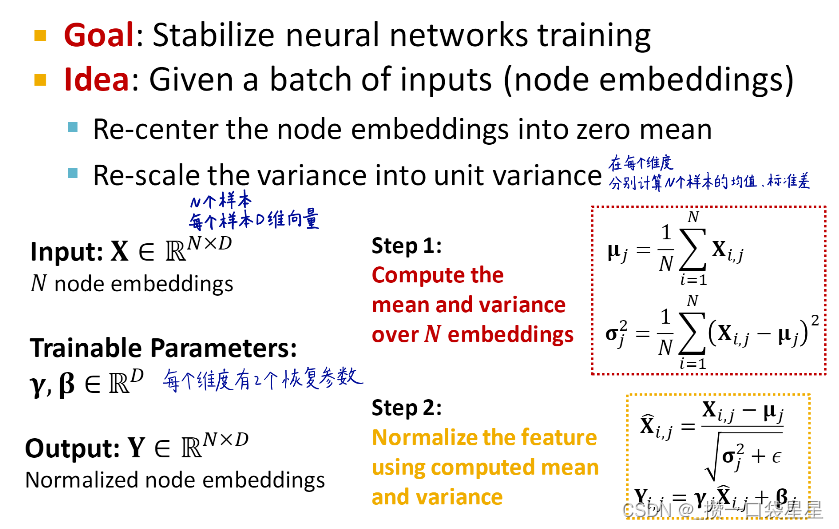
2. batch normalization:标准化
   
3. dropout:防止过拟合
   
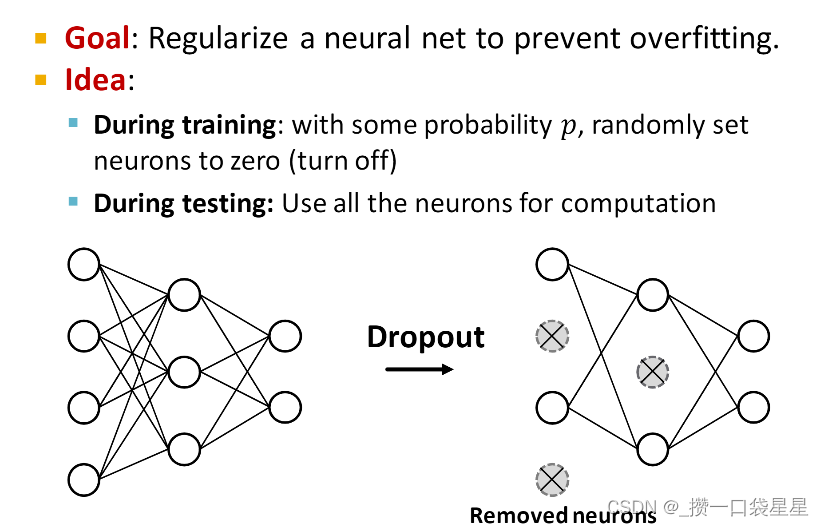
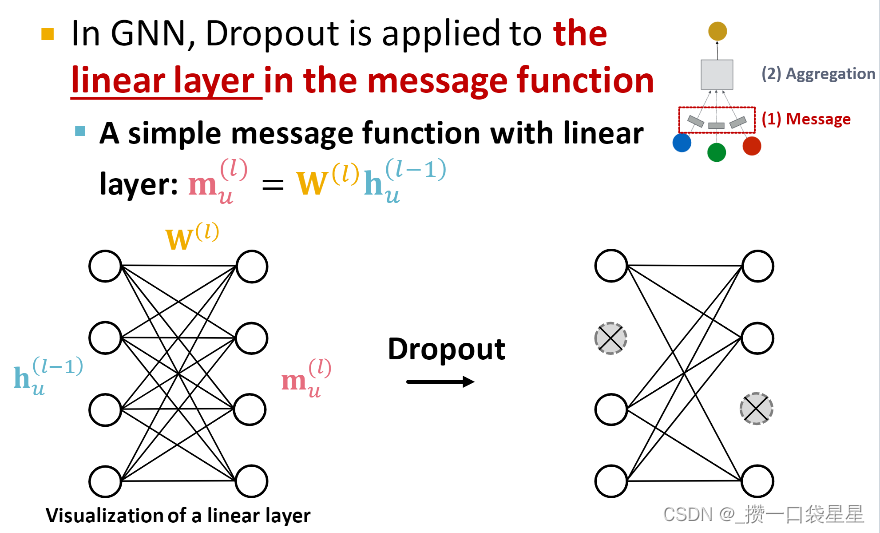   4. activation 非线性
   
4. 小结

3.1.4 GNN layers stacking

• 按顺序堆叠layers
• 输入：原始节点属性特征，输出：节点嵌入
  

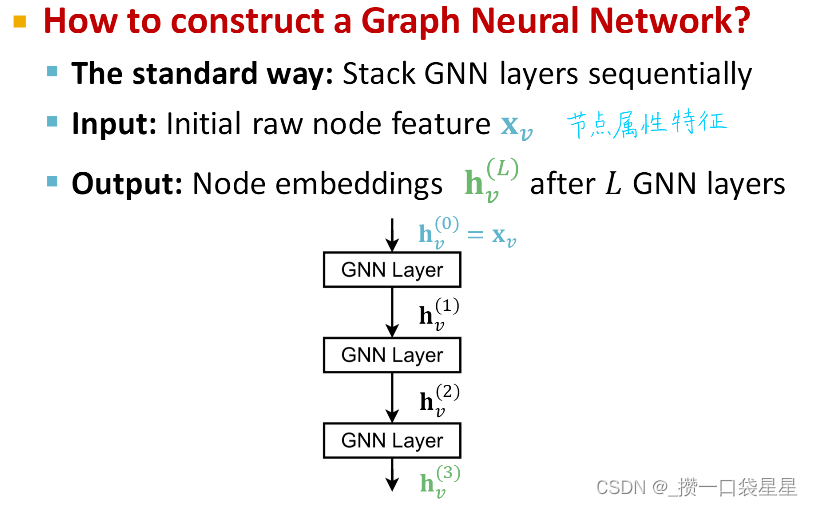
1. 过度平滑问题
   GNN层数不能过深

• 所有节点的嵌入相同

K层GNN的感受野：决定节点嵌入的节点集合

• 共享邻居节点随着GNN层数的增加快速增加
  
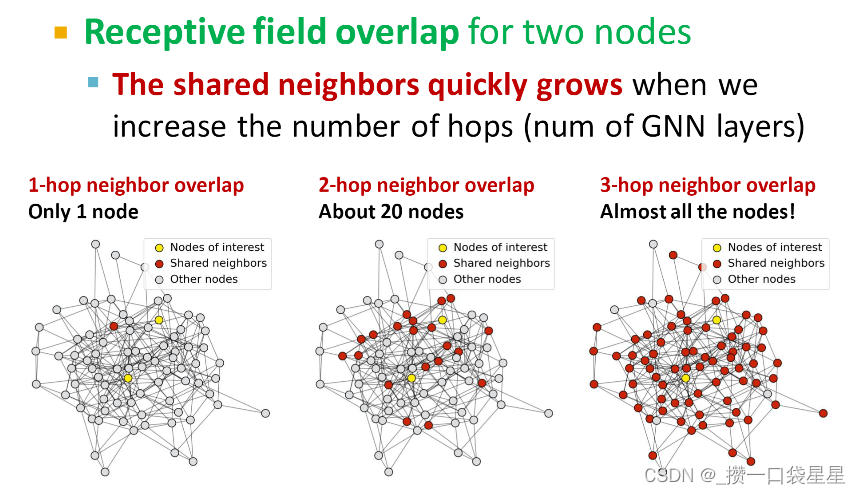
  一个节点的嵌入取决于它的感受野，如果两个节点有高度重合的感受野，那么他们的嵌入就会非常相似
  ---->出现过度平滑的问题
  解决方法：从GNNlayers的连接入手
  （1）不能无脑堆很多层
  第一步：计算必要的感受野（例如计算图的直径）
  第二步：将GNNlayers的个数稍稍大于我们需要的感受野，可以用automl找到最优的层数

如果GNN层数很小，如果提高GNN的表示能力？
1）在GNN层的内部加上深度神经网络
在之前的例子中，邻域信息转换或聚合只有一个线性层
2）预处理和后处理
在GNN层的前后加MLP层

如果需要很多GNN 层呢？
解决方法（2）在GNN中增加skip connections
GNN靠前层（感受野较小的层）的节点嵌入能够较好的区分节点—>通过裁剪增加前面层的影响

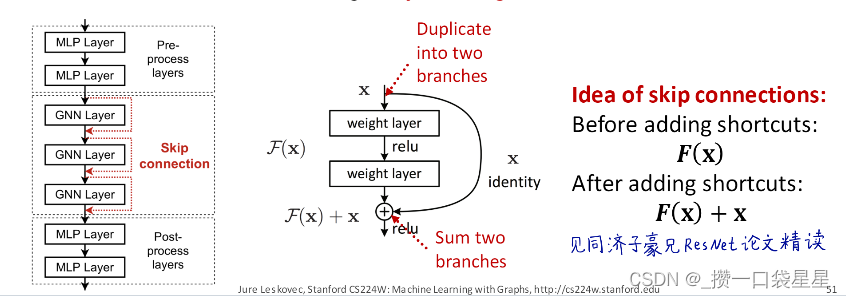
skip connections可以创造混合模型

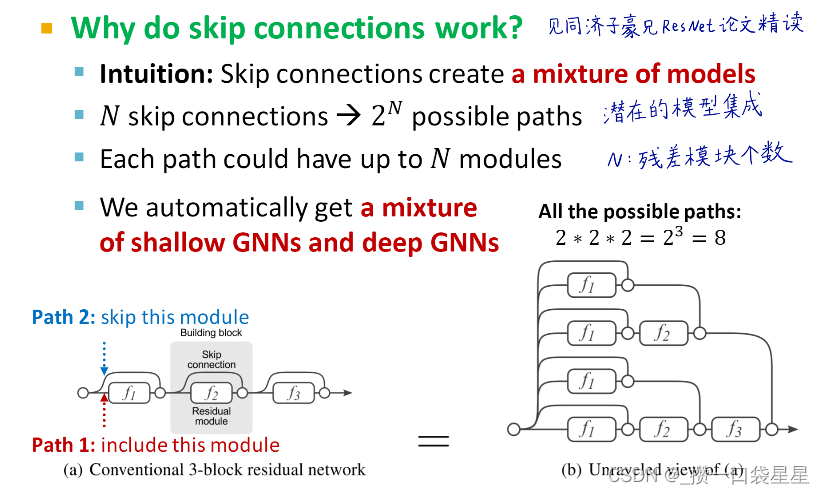
例子:GCN with skip conections

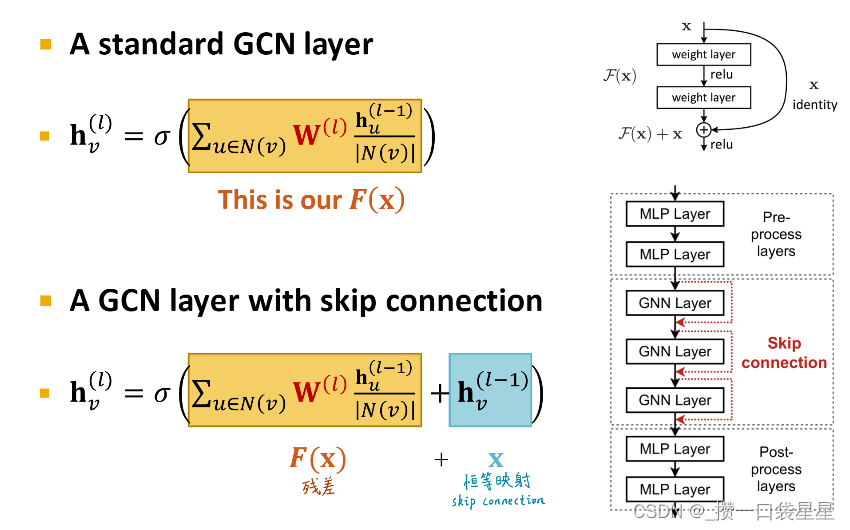
其他例子;

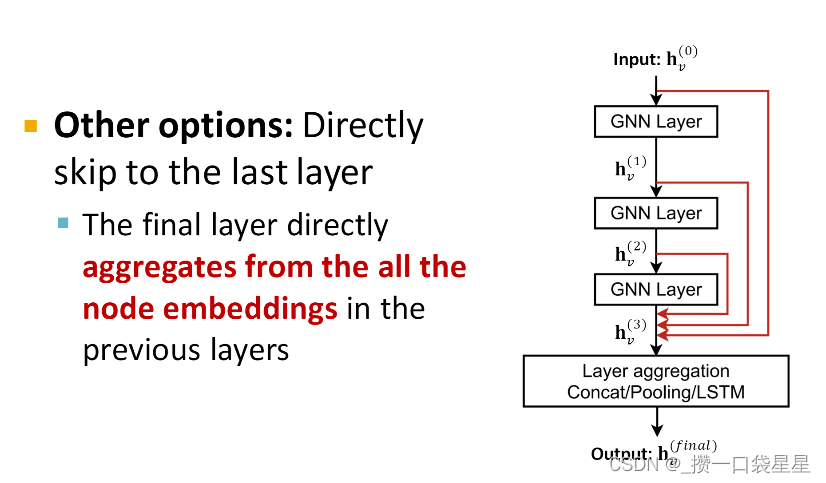
3.1.5 输入图和特征的扩增

在这之前，都是假设原始图==计算图
但是，

• 节点特征层面，输入图缺少节点特征—>特征增强
• 图结构层面
  • 太过稀疏—消息传递效率低—>添加虚拟节点和边
  • 太过稠密—消息传递耗资源—>消息传递时对邻居节点采样
  • 太大—计算图与GPU不匹配—>计算嵌入时采样子图
• 原始图 不太可能 恰好就是最优的计算图

1. 为什么要进行特征增强？
   （1）正常情况下我们只有邻接矩阵，没有节点属性
   （a)给节点分配一个常数，也可以是固定长度的常数向量
   （b)给节点分配一个唯一ID编号，这些ID编号转化成独热向量
   
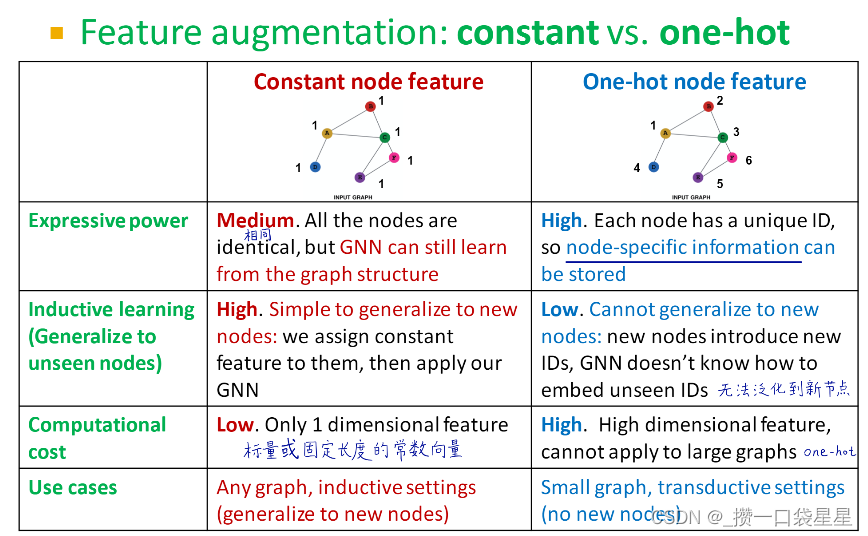
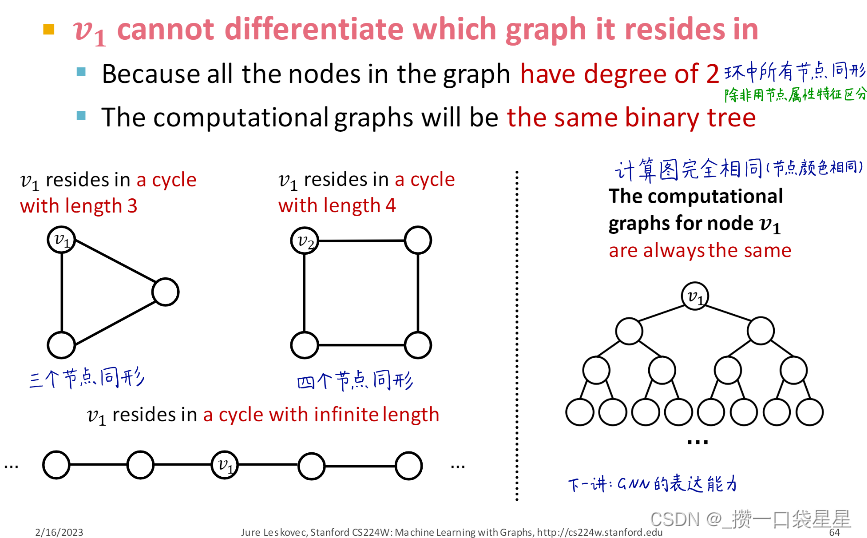
   （2）用GNN很难学习一些图结构
   例如：数节点所在环的长度，GNN学不到

• 因为所有节点度相同（除非有属性特征）
• 计算图是相同的二叉树
  
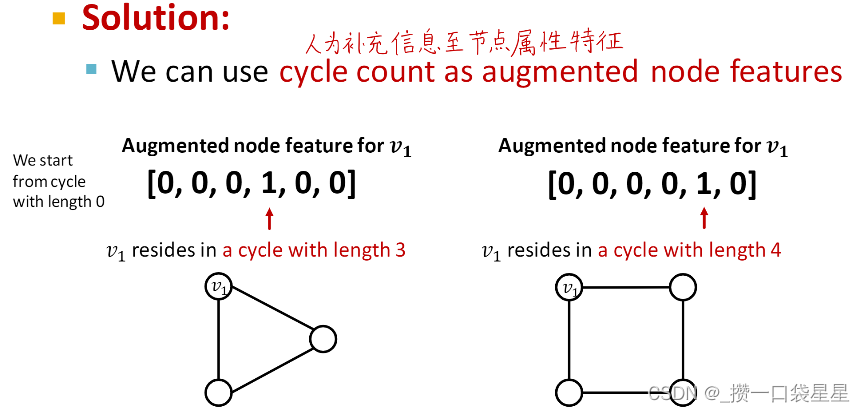
  解决方法：人为补充信息至节点属性特征
  
  

2. 添加虚拟节点和边
   目的：增强稀疏图
   （1）虚拟边
   
   （2）虚拟节点
   
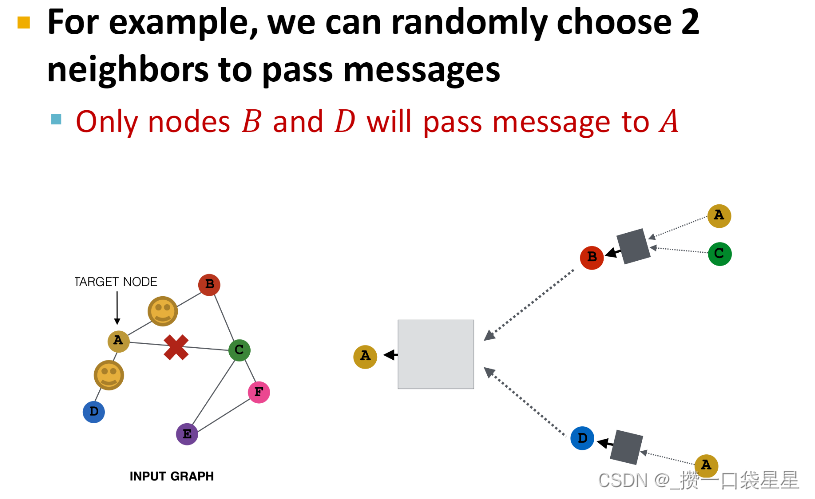
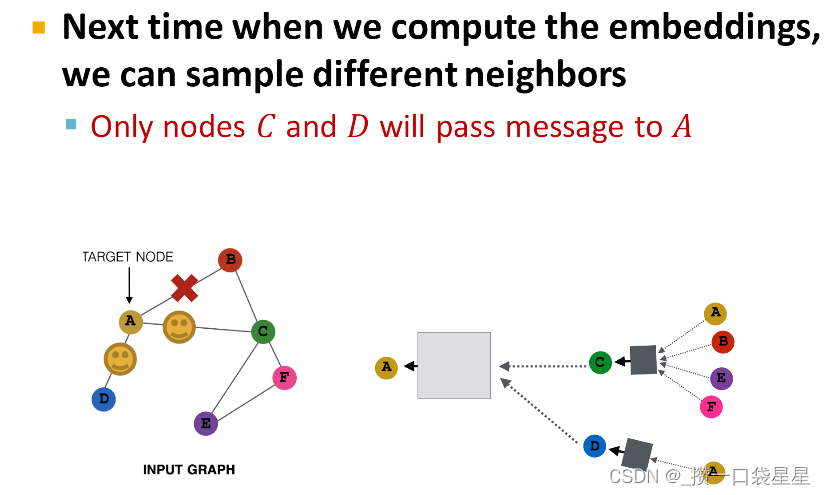
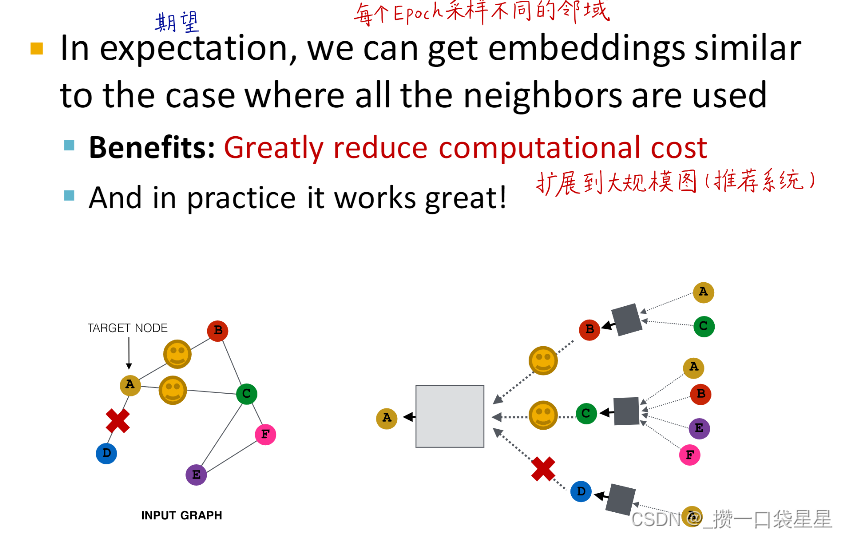
3. 消息传递时对邻居节点采样
   目的：稠密图（所有节点用来传递消息）
   该方法是对选取部分节点用来传递信息
   
   
   

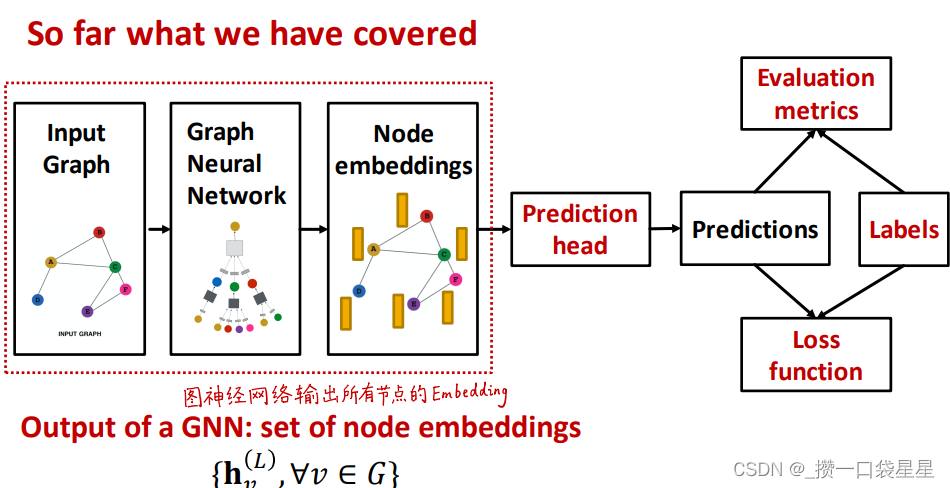
3.1.6 GNN训练–rediction head

以上步骤可以得到节点嵌入，下一步是prediction head

• 节点层面
• 边层面
• 图层面
  不同的预测任务需要不同的prediction head
  
  (1) 节点层面
  经过GNN计算，得到了节点的D维向量，可以直接使用节点嵌入进行预测
  可以进行分类（k个类别的概率）或者回归（k个连续值）
  
  （2）边层面
  用节点嵌入对进行预测
  
  （a)联结+线性
  
  （2）点乘
  
  （3）图层面
  用所有节点的嵌入进行预测
  
  

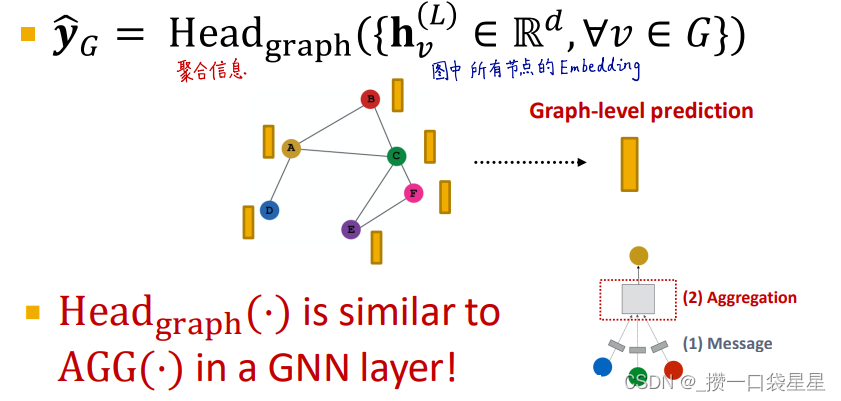
以上方法在小图中效果很好，在大图中会丢失信息，在大型图中怎么做呢？
比如在下面的例子中，两个图的预测结果相同。

—>解决方法：分层聚合节点嵌入

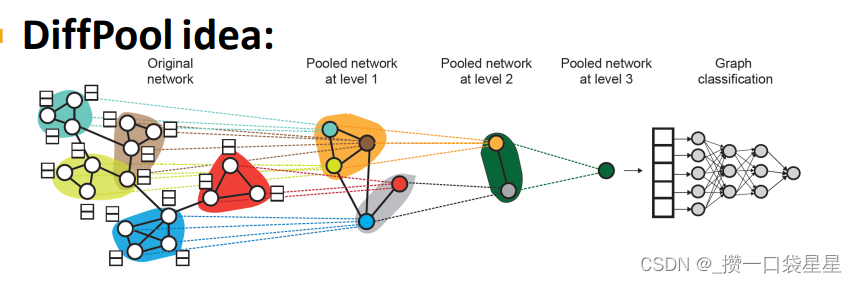
示例1：社群分层池化
a.分层池化
b.利用2个独立的GNN，A计算节点嵌入，B计算节点聚类
c.两个GNN可以同时执行

对于每个池化层

• 使用GNN B的聚类结果来聚合GNN A生成的节点嵌入
• 为每个集群创建一个新节点，保持集群之间的边缘以生成一个新的池网络
  联合训练GNN A和GNN B
  

3.1.7 GNN 训练—预测和标签

1. 真实值来自监督学习中的标签或者无监督学习的信号
   
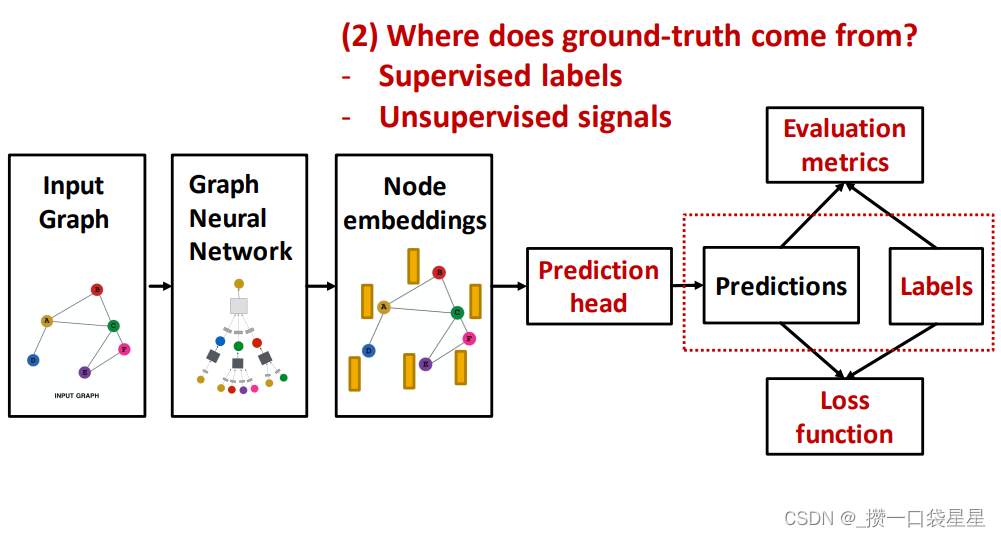
2. 监督学习和无监督学习
   blurry模糊不清的
   
   监督学习标签，不同案例标签不同
   
   无监督学习
   

3. 1.8 GNN训练—损失函数

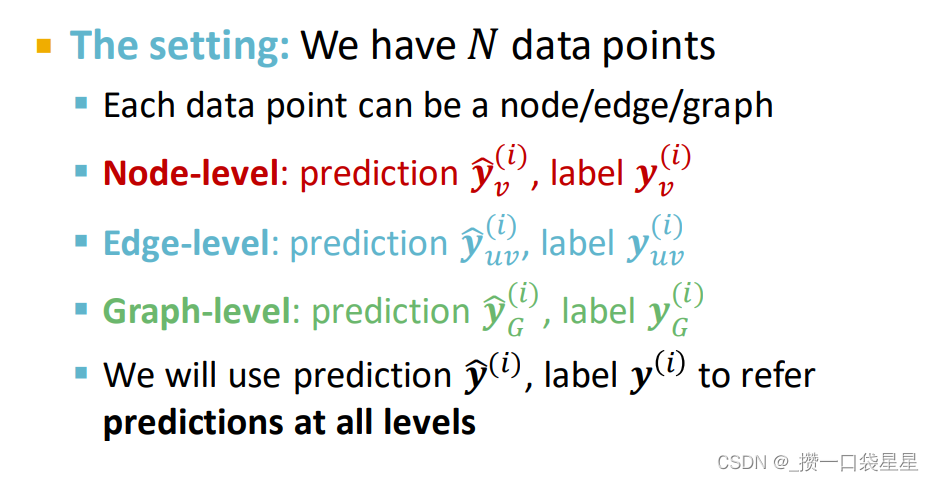
分类，结果为离散值；回归，结果为连续值。GNN可以应用于这两种情况。
不同之处在于损失函数和评价指标

1. 分类的损失函数
   交叉熵
   
2. 回归的损失函数
   

3.1.9 GNN 训练–评价指标

精确度和混淆矩阵，可以用sklearn实现

1. 回归
   
2. 分类
   
   
   
   

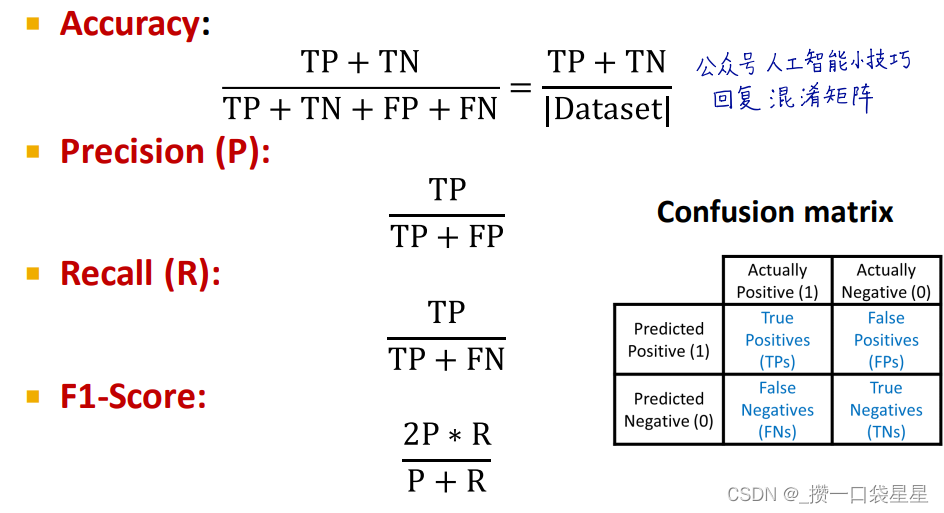
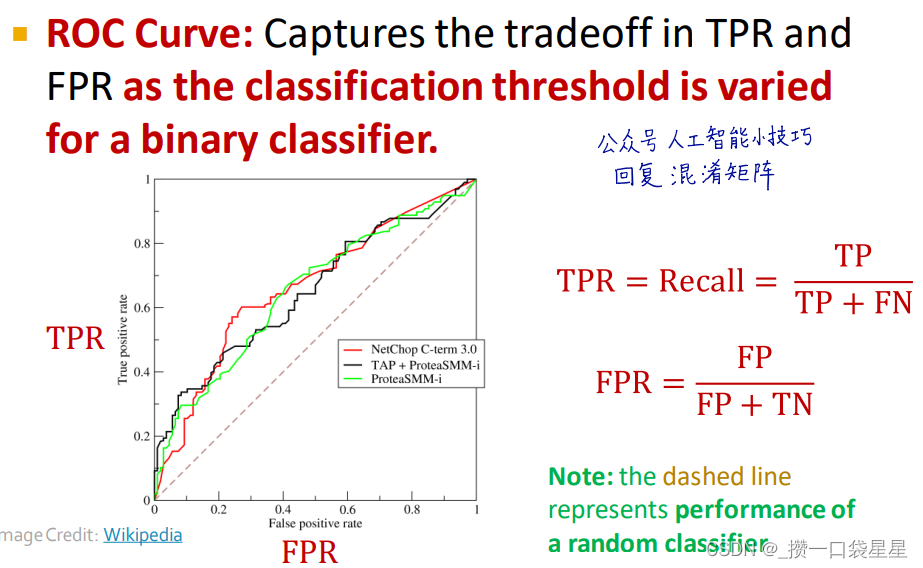
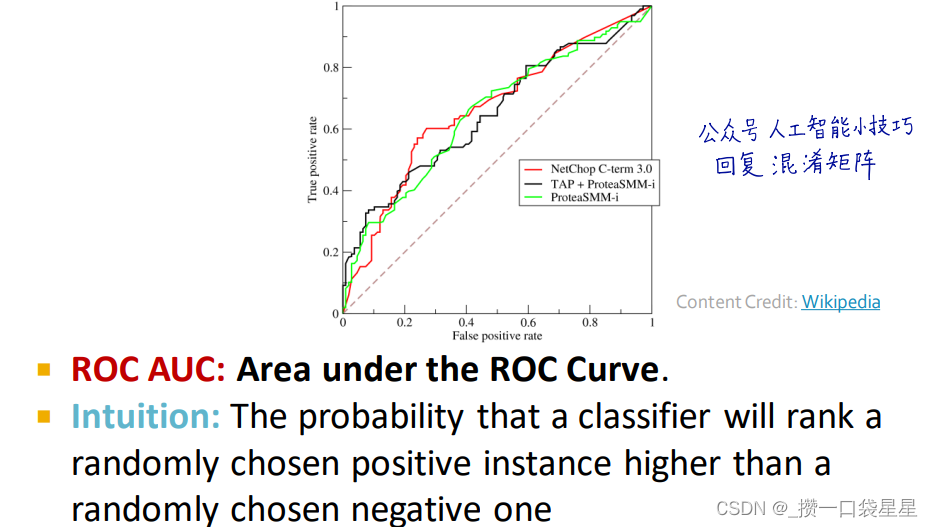
3.1.10 建立GNN 预测任务

如果分配训练集、验证集、测试集

1. 数据集分配方法： 固定分配、随机分配
   
   对于图像分类，每个图像是一个数据，样本之间独立同分布
   但是对于节点分类，节点之间并不是独立同分布的，所以训练集节点的计算图中可能出现测试集节点
2. GNN 中如何分配？
   （1）直推式学习
   输入图在训练、验证和测试时都可以用，只分配标签
   训练时，用整图计算节点嵌入，训练时采用1、2节点的标签
   验证时，用整图计算节点嵌入，采用3、4节点的标签评价
   
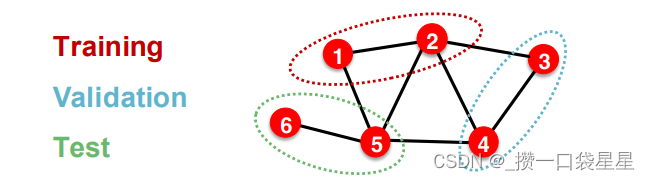
   （2）归纳式学习
   将分配集之间的边打断，得到多个子图，得到的三个图时相互独立的
   训练时，用节点1、2计算嵌入，节点1、2训练
   验证时，用3、4计算嵌入，3、4评价

比较：
直推式学习，训练验证和测试在同一个图上，用节点标签分配，只能用于节点预测和边预测任务
归纳式学习，训练验证和测试在不同的图上，可以用于节点预测、边预测和图任务中。好的模型应该可以泛化到新图

例子：
a.节点分类：直推式和归纳式
b.图分类：归纳式

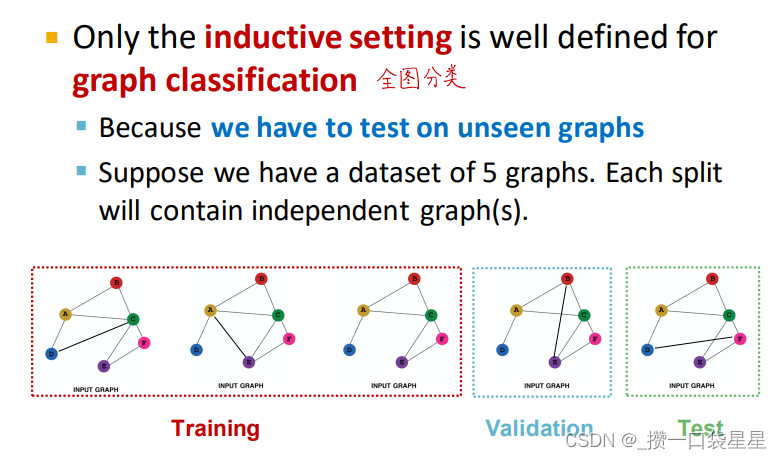
c.边预测：预测缺失的边
一个无监督/自我监督的任务。我们需要自己创建标签和数据集
具体来说，我们需要对GNN隐藏一些边，并让GNN预测这些边是否存在
第一步：创建数据集，一部分边作为message edges 一部分作为supervision edges(应该隐藏起来）

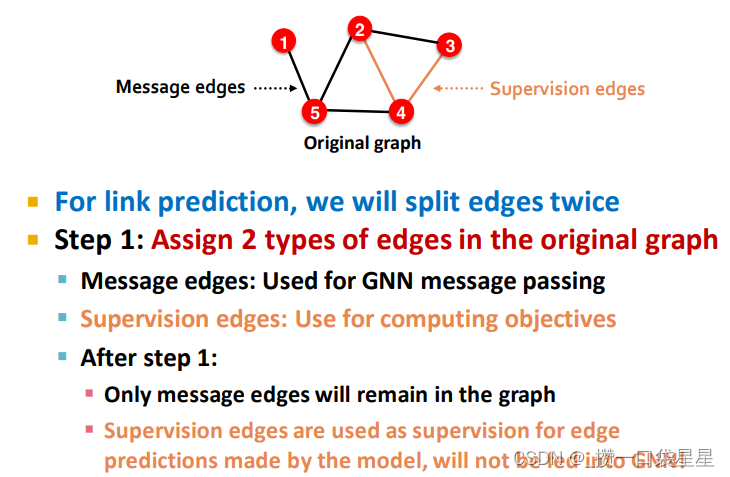
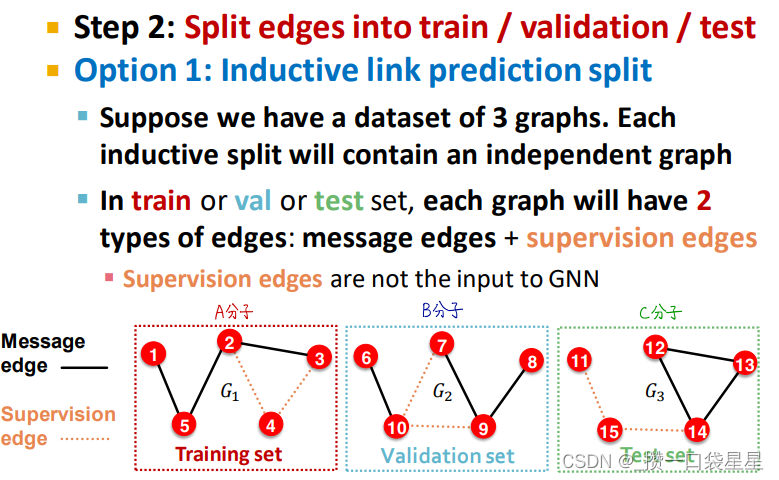
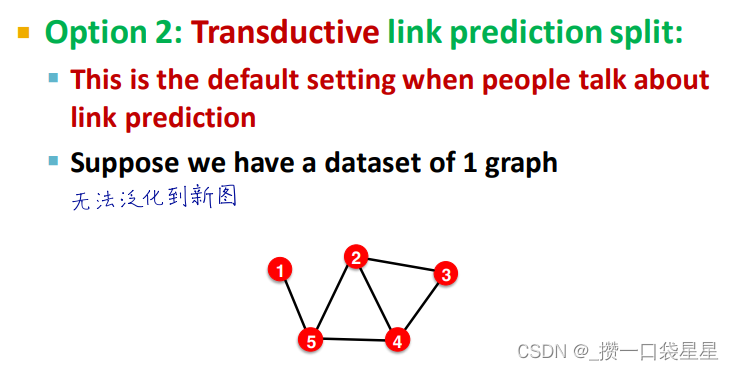
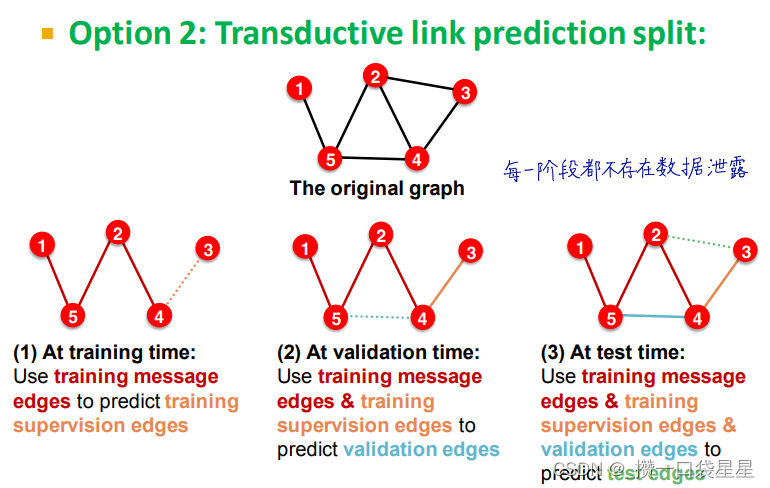
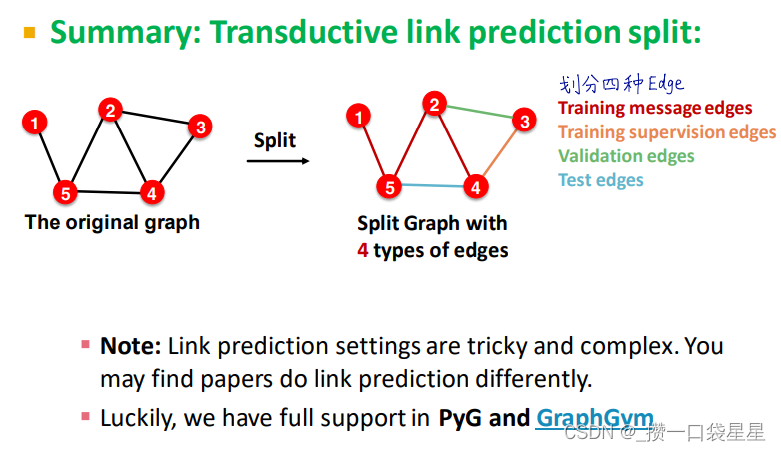
3.2 GNN的表示能力

神经网络有万能近似定理
图神经网络的表达能力：区分不同图结构的能力

3.2.1 GNN基础概念

1. 单个GNN layer
   信息计算：$m_u^l=MS{G}^l(h_u^{l-1})$
   信息聚合：$h_u^l=AG{G}^l(m_u^{l-1},u\in \mathbb{N}(v))$

2. GNN model
   GCN 对应元素求均值+线性+ReLU非线性
   GraphSAGE 多层感知器+d对应元素max-pooling
   

• 可以用不同颜色表示不同的节点嵌入，例如表示节点的属性特征，
• 计算图中通过连接结构区别不同节点

3.2.2 GNN如何区分不同图结构

1. 局部邻域结构

• 如果只考虑节点的局部邻域结构
  节点度不同，邻居的节点度不同
  但是当两节点对称时，仅通过图的连接结构是无法区分的，如下图的节点1、2
  

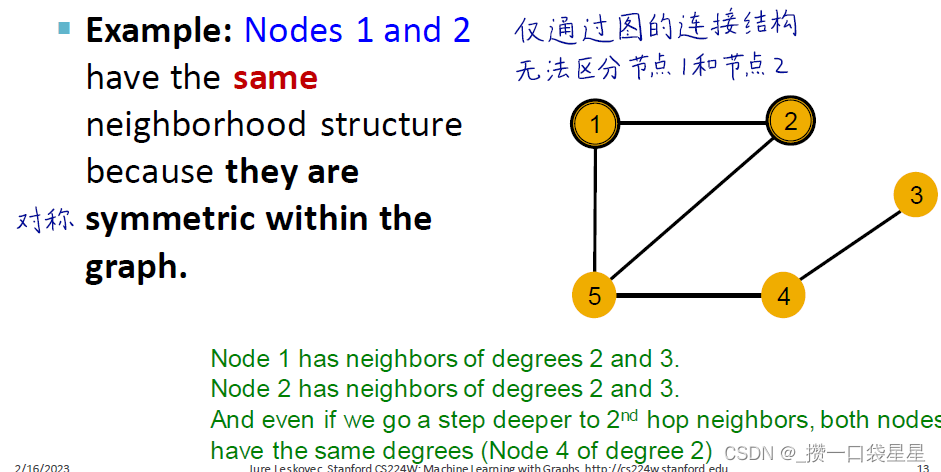
2. 关键问题：GNN节点嵌入是都能够区分不同节点的局部邻域结构？

（1）从计算图入手，GNN的表达能力=区分计算图根节点嵌入的能力
在每一层，GNN聚合了邻居节点的嵌入信息，但是GNN 不关心节点编号，它只是聚合了不同节点的特征向量。
不同局部邻域定义不同的计算图，计算图与每个节点周围的根节点子树结构相同

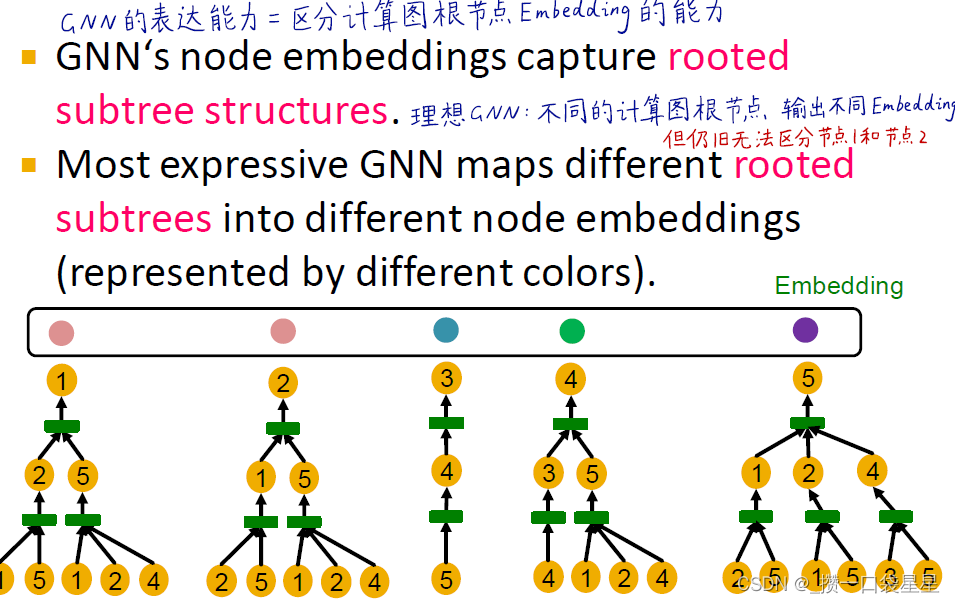
（2）引入单射函数（每个输入对应唯一输出，包含了所有的输入信息）
将不同的根子树映射到不同的节点嵌入中，先获得树的单个级别的结构，然后利用递归算法得到树的整个结构
（3）如果GNN聚合的每一步都可以完全保留相邻信息，则生成的节点嵌入可以区分不同的有根子树
（4）理想GNN：不同的计算图根节点输出不同的Embedding
最具有表达力的GNN：聚合操作应该单射
最完美的单射聚合操作：哈希

3.2.3 设计最具表现力的GNN

1. 首先：

• GNN的表达能力可以通过使用邻域聚合函数来表征
• 更具表现力的聚合函数会使得GNN更具表现力
• 单射聚合函数可以得到最具表现力的GNN

2. 理论分析聚合函数的表达力
   邻居聚合可以概括为一个超集（multi-set,一个有重复元素的集合)函数
   

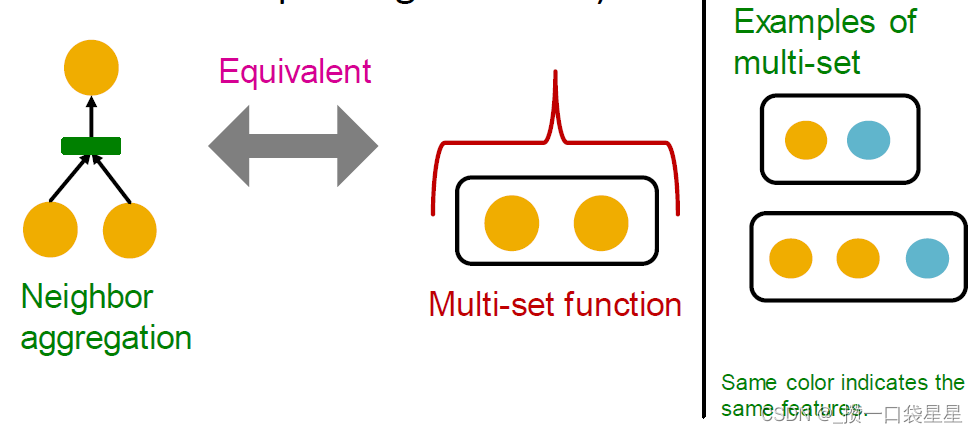
3. 分析两个GNN模型的聚合函数

• GCN的聚合函数（平均池化层）：逐元素求平均+线性+ReLU激活
  无法区分颜色比例相同的不同超集，如下图（比例相同，求均值激活后输出相同），这个就不是单射函数
  
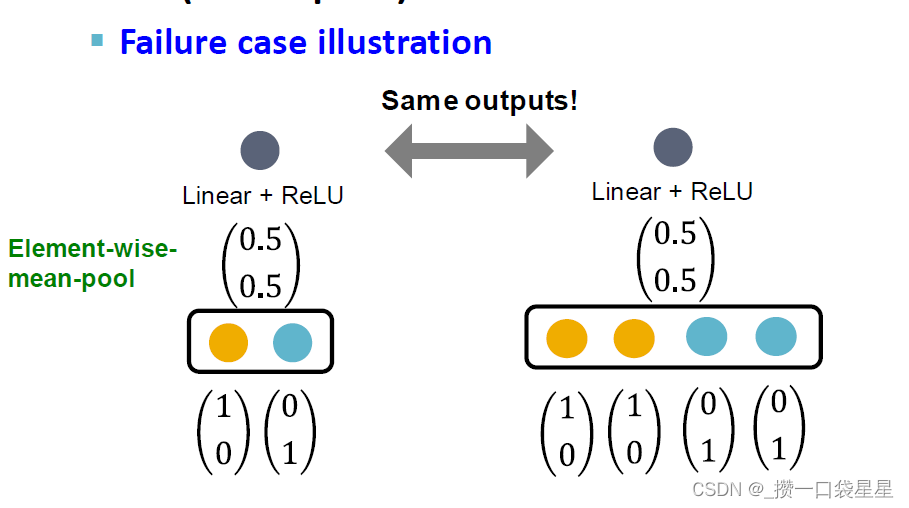
• GraphSAGE的聚合函数无法区分不同的超集与同一集合下的不同颜色，逐元素求最大值
  

4. 小结

• GNN的表达能力可以用邻居聚合函数的表达能力来表征。
• 邻居聚合是一个多集(具有重复元素的集合)上的函数
• GCN和GraphSAGE的聚合函数不能区分一些基本的多集;不是单射。
• GCN和GraphSAGE并不是最强大的GNN

3.2.4 设计表达力最强的GNN—GIN

1. 目标：
   在信息传递GNN设计表达力最强的GNN，通过在多重集合上设计单射邻域聚合函数来实现
   —>用神经网络拟合单射函数（神经网络的万能近似定理）

2. 任何单射多集函数都可以表示为 $\Phi (\sum _{x\in S}f(x))$
   
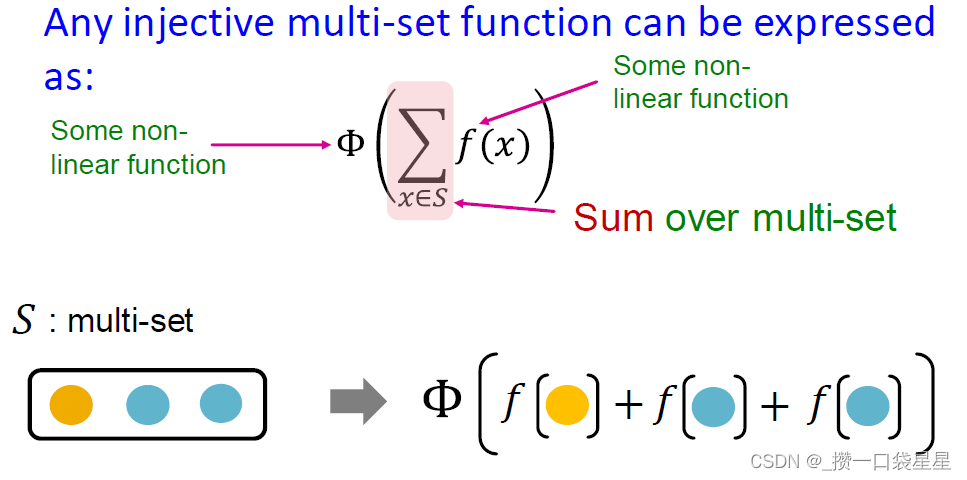
   例子：f产生颜色，求和记录颜色个数，Φ是单射函数
   

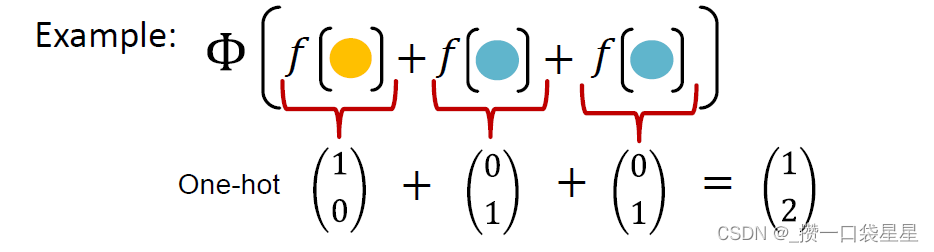
3. 如何建立Φ和f呢？GIN网络

• 万能近似定理，使用多层感知机
  在具有一个隐藏层的MLP模型中，当隐藏层的维度足够大，且使用非线性函数可以将任何连续函数近似到任意精度

• $ML{P}_{\Phi }(\sum _{x\in S}ML{P}_f(x))$
  实际中，MLP隐藏层的维度100-500是足够的

4. GIN网络
   GIN 与 WL 图核（传统提取图级特征的方法见L3）
   算法步骤：
   第一步：初始化每个节点的颜色$c^{(0)}(v)$
   第二步：对节点的颜色进行迭代更新 $c^{(k+1)}(v)=HASH(c^{(k)}(v),{c^{(k)}(u)}_{u\in N(v)})$
   

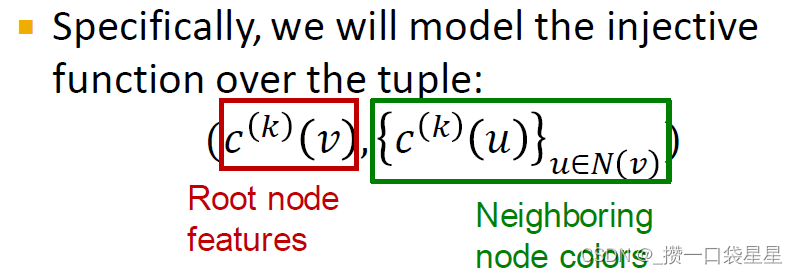
第三步：迭代停止得到节点 颜色

任何一个单射函数可以表述为以下形式：$ML{P}_{\Phi }((1+ϵ)ML{P}_f(c^{(k)}(v)+\sum _{u\in N(v)}ML{P}_f(c^{(k)}(u))$

如果输入特征$c^{(0)}(v)$表示为独热向量，那么直接求和的函数就是单射函数（不需要f)
单射函数：


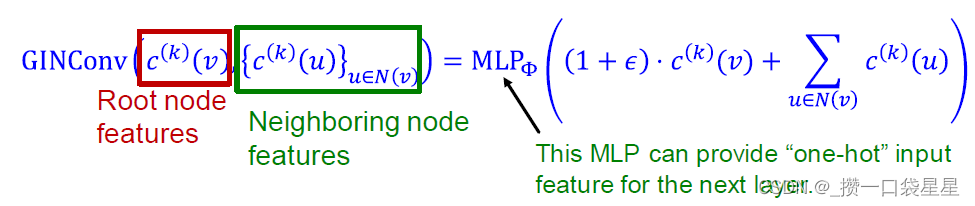
5. GIN 与 WL graph kernal
GIN可以理解为WL graph Kernel的可微神经版本

GIN相对于WL图内核的优点：
a.节点嵌入是低维的；因此，它们可以捕获不同节点的细粒度相似性
b.可以根据下游任务学习优化

6. 总结
   WL是表达能力的上界，如果两个图可以用GIN区分，那么也可以被WL kernal.反之亦然
   WL kernal在理论上和经验上可以区分真实世界的大部分图
   GIN也足够强大，可以区分大多数真实的图!

3.2.5 问题：对称的依然不能去区别

有循环的依然不能区分

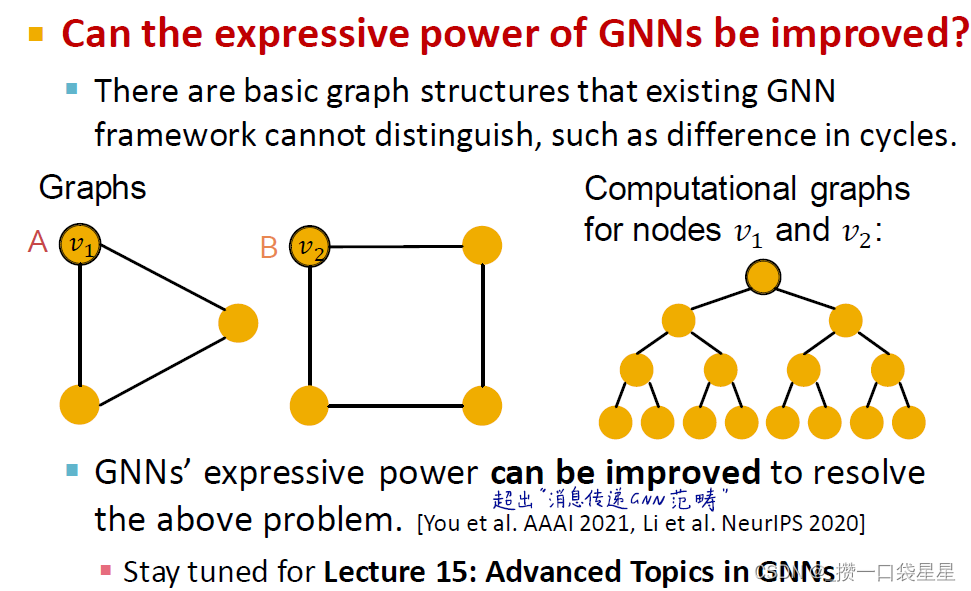
3.2.6 问题与解决方案

1. 通用解决方案

• 数据预处理：特征标准化处理
• 优化器：使用ADAM优化器
• 激活函数：ReLU通常效果很良好，可使用LeakyReLU、PReLU等其他激活函数，输出层没有激活函数，每一层包含偏置项
• 嵌入维度：通常选择32、64和128

2. 调试深度网络

• Debug问题：损失/准确值在训练时未收敛
  • 检查pipeline
  • 调整学习率等超参数
  • 注意权重参数初始化
  • 仔细观察损失函数
• 模型开发：
  • 在训练集上存在过拟合情况
    用一个小的训练数据集，损失应该基本上接近于O，具有表达性的神经网络
  • 检查loss曲线

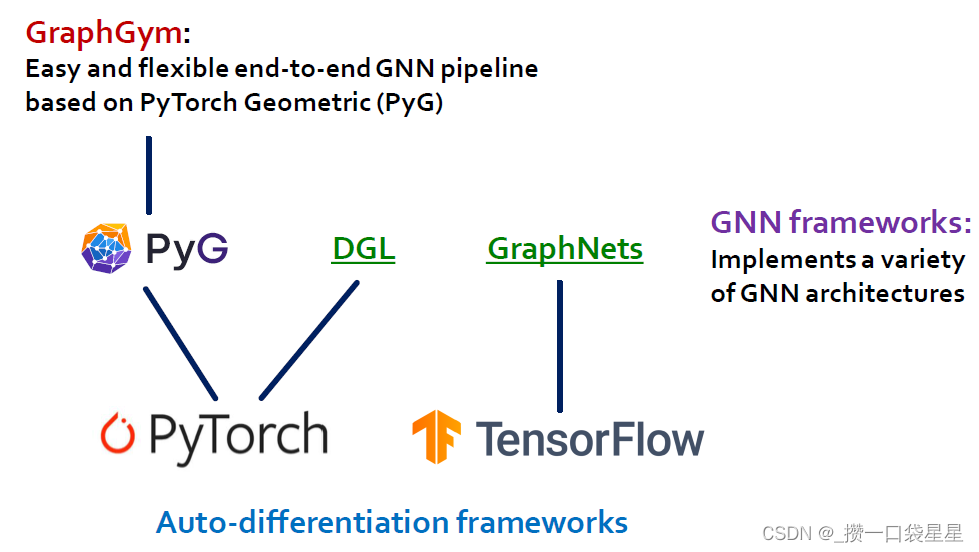
3.2.7 Resources on GNN

用pytorch比较好

3.3 GCN

GCN的基本思想： 把一个节点在图中的高纬度邻接信息降维到一个低维的向量表示。
首先，我们取其所有邻居节点的平均值，包括自身节点。然后，将平均值通过神经网络。请注意，在GCN中，我们仅仅使用一个全连接层。
GCN的优点：

• 1. 可以捕捉graph的全局信息，从而很好地表示node的特征。捕捉功能结构角色的信息，deepwalk和node2vec不可以
• 2. 充分利用属性信息
• 3. 算法复杂度线性增加
     GCN的缺点：
• 1. Transductive learning的方式，需要把所有节点都参与训练才能得到node embedding，无法快速得到新node的embedding。
• 2. 融合时边权值是固定的，不够灵活。
• 3. 层数加深时，结果会极容易平滑，每个点的特征结果都十分相似。

3.3.1 数学形式

1. 基本形式
   
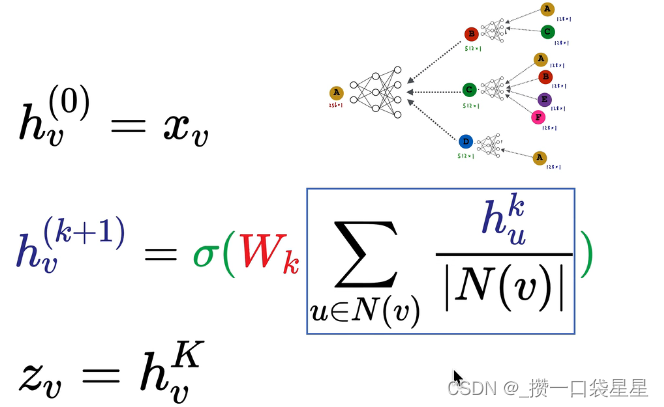
   左乘A邻接矩阵是求和，左乘D的逆矩阵是求平均的过程。其中D矩阵是一个度对角矩阵，值为每个节点的连接数
   
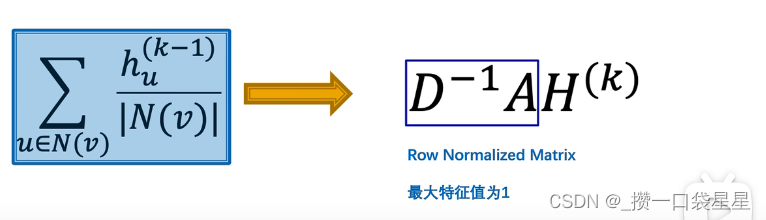
   RNM 互为转置，非对称矩阵，最大特征值为1；只按自己的度，对所有渠道来的信息求平均，没有考虑对方的连接数
2. 改进：$D^{-1}A{D}^{-1}$
   对称矩阵，既考虑了自己的度，也考虑了对方的度。
   特征值在-1至1之间，输入向量左乘该矩阵后，幅值会变小
3. 不想幅值变小：$D^{-1/2}A{D}^{-1/2}$
   对称矩阵，特征值在-1至1之间，最大特征值为1

3.3.2 最终形式

有邻域和自己

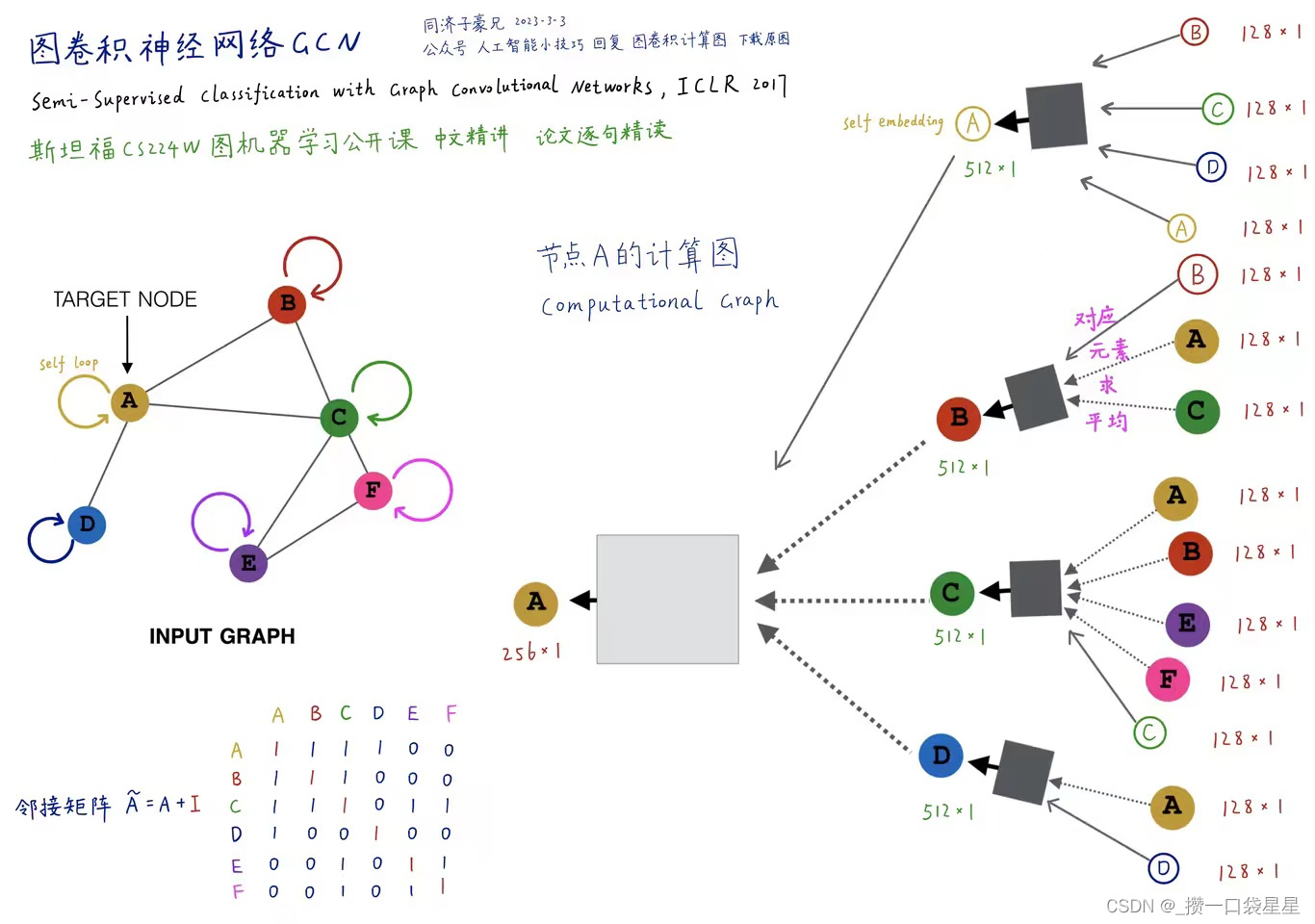
邻域和自己权重可以不同

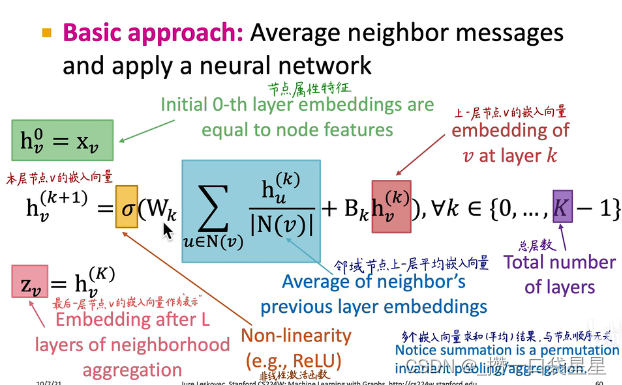
3.4 GAT

通过给每条边加了一个模型可学习的系数 ，进行带attention系数的node feature融合，使得在做卷积融合feature的过程，能够根据任务调整模型参数，变得自适应使得效果更好。

3.5 GraphSAGE

具体的思想就是分三步：

1. 采子图：训练过程中，对于每一个节点采用切子图的方法，随机sample出部分的邻居点，作为聚合的feature点。如下图最左边，对于中心点，采两度，同时sample出部分邻居节点组成训练中的子图。
2. 聚合：采出子图后，做feature聚合。这里与GCN的方式是一致的，从最外层往里聚合，从而聚合得到中心点的node embedding。聚合这里可操作的地方很多，比如你可以修改聚合函数（一般是用的mean、sum，pooling等），或增加边权值都是可以的。
3. 任务预测：得到node embedding后，就可以接下游任务了，比如做node classification，node embedding后接一个linear层+softmax做分类即可。
   
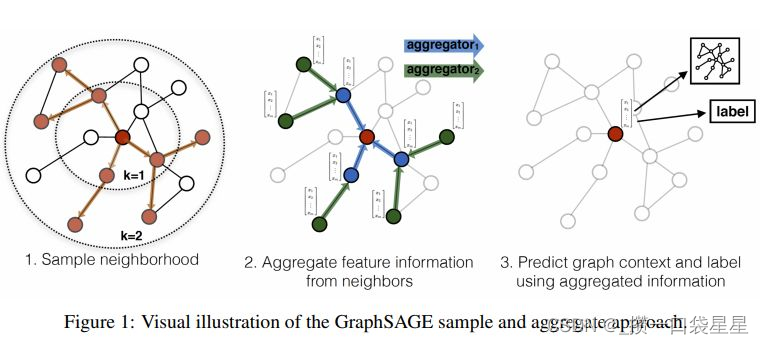
   1.解决了预测中unseen nodes的问题，原来的GCN训练时，需要看到所有nodes的图数据。2.解决了图规模较大，全图进行梯度更新，内存消耗大，计算慢的问题