机器人运动学及轨迹规划— (2)DH建模与正运动学方程_机器人运动学dh模型

1、DH参数法建模

       可以将机器人各轴看成由一系列关节连接起来的连杆组成，将坐标系固连在每一个连杆关节上，则可以通过齐次变换来描述这些坐标系之间的相对位置和方向。这种通过齐次变换建立机构的运动学模型被称为D-H参数法，在DH参数模型下机器人各连杆的关系可以用a、alpha、d、theta 四个参数表示，其中theta为关节角度，d为相邻关节距离，a为连杆长度，alpha 为连杆扭角。

       目前DH参数法一般分为标准SDH（standard DH）与改进DH（modified DH），标准DH将固连坐标系定义在连杆的末端，而改进DH则是将坐标系定义在连杆的前端。MDH适用范围更广，更容易理解和推导，本文采用MDH对ABB的IRB2600-1.65型号机器人进行建模，由于后三轴坐标系建立在腕部，到法兰的距离在matlab机器人工具箱中难以体现，因此对MDH参数建模的验证在ABB的离线编程仿真软件RobotStudio中进行。

（1）SDH

        SDH的变换顺序为θ、d、a、α

        因此转换矩阵为： 

 

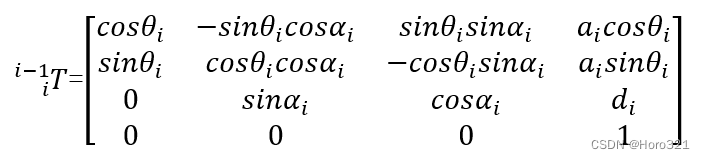
（2）MDH

      MDH的变换顺序为α、a、θ、d：

       则转换矩阵为：

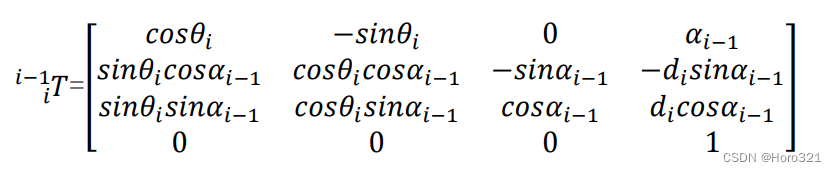
       对于IRB2600型号机器人，首先确定各关节轴 J1-J6：

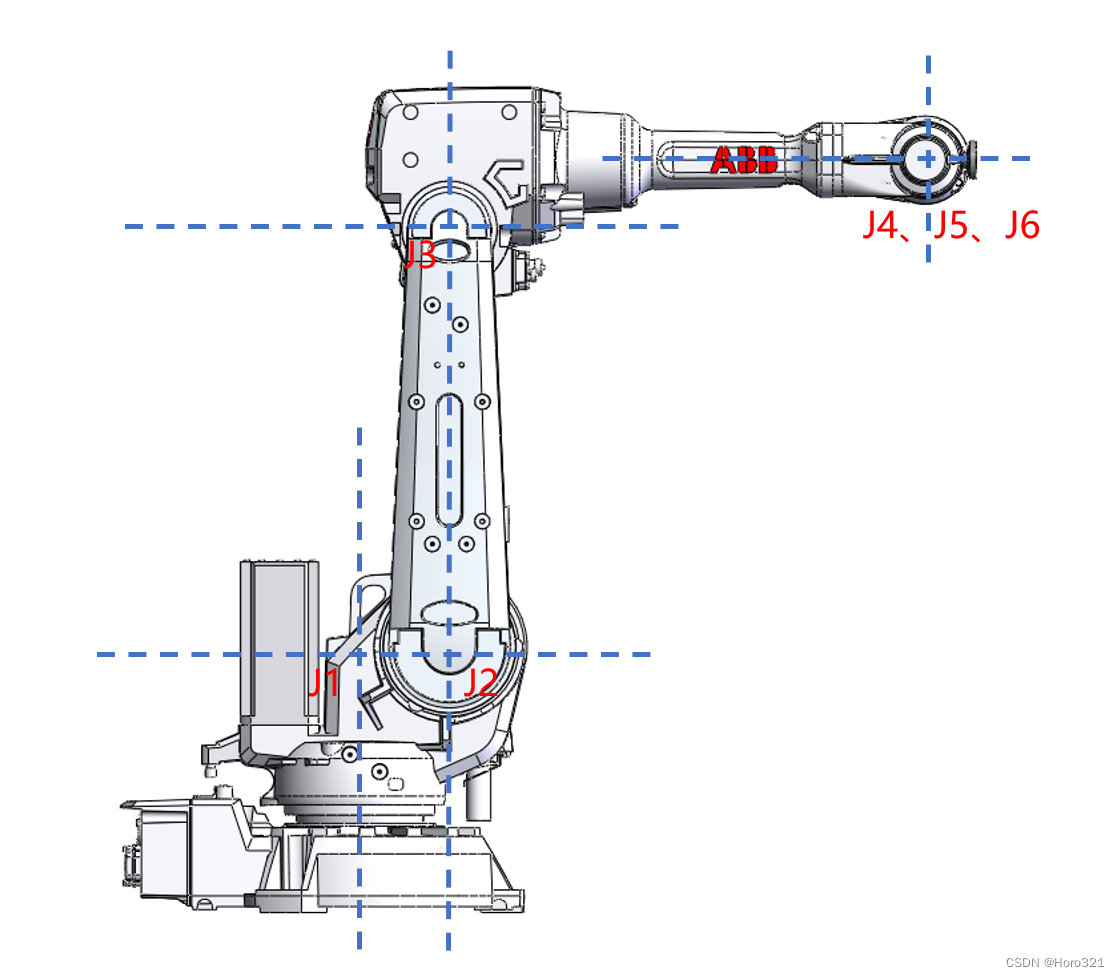
        此时Z轴方向已知确定X和Y轴方向：

        X轴方向为由(Z)关节轴线i指向i+1。

        Y轴方向由右手法则确定（右手握拳，螺旋方向与Z轴转向X轴方向一致，拇指指向为Y轴正方向）。

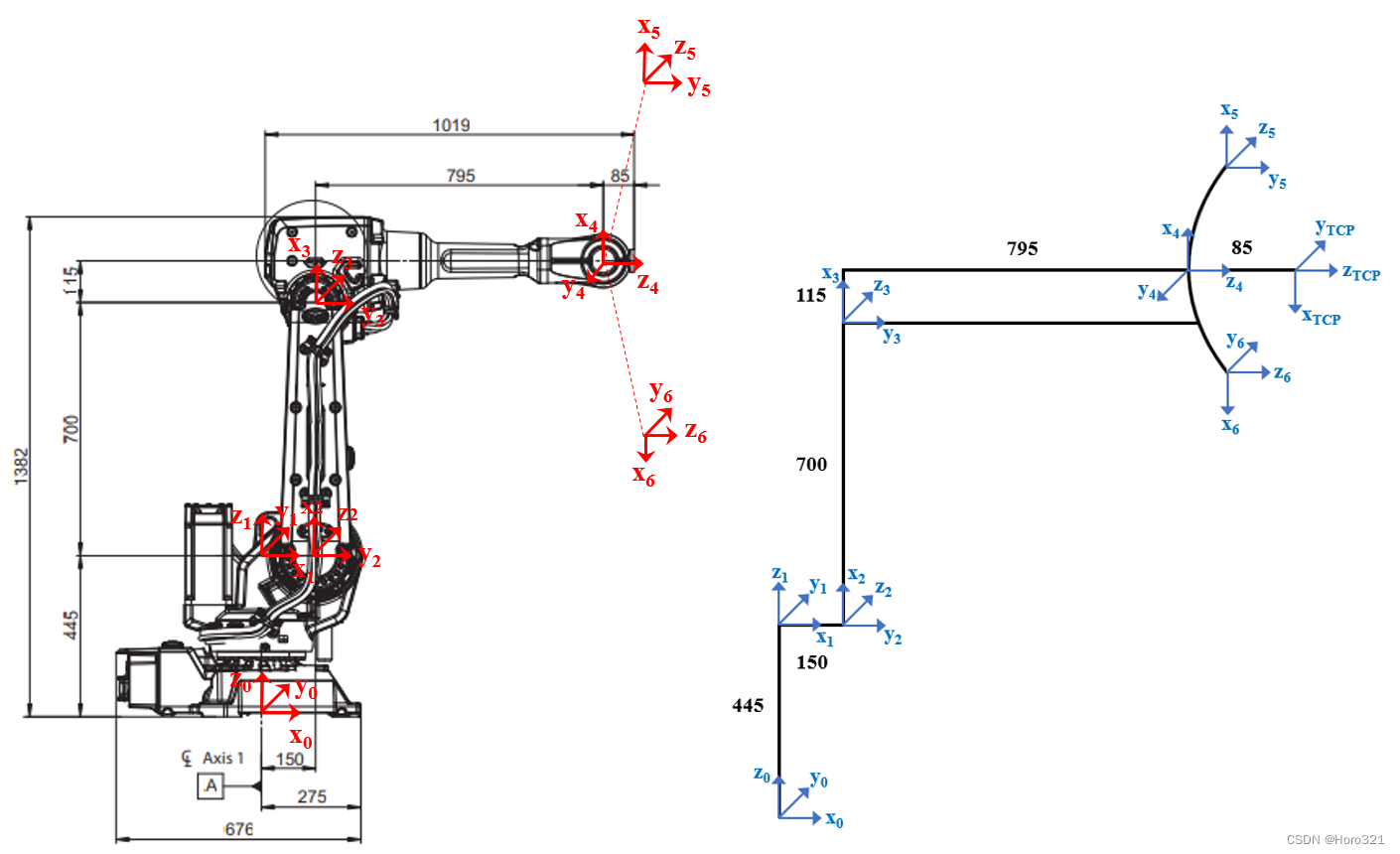
        求得的DH参数为：

2、建立正运动学方程

       正运动学是给定机器人关节空间下的各关节角度，来求解机器人末端位姿，即将关节空间的关节变量转换为笛卡尔空间的位置和姿态。

       将MDH参数代入转换矩阵得：

        将矩阵输入matlab计算给定关节角度下的位姿：

function [T06]=mymodfkine(theta)
%改进DH参数建模  正运动学
theta1 = theta(1,1);
theta2 = theta(1,2);
theta3 = theta(1,3);
theta4 = theta(1,4);
theta5 = theta(1,5);
theta6 = theta(1,6);
%    theta        d       a         alpha
MDH=[theta1       0.445      0              0;
     theta2-pi/2    0        0.150      -pi/2;
     theta3         0        0.700          0;
     theta4        0.795     0.115      -pi/2;
     theta5         0        0           pi/2;
     theta6-pi      0        0         -pi/2];
 
 T01=[cos(MDH(1,1))         -sin(MDH(1,1))           0                    0;
      sin(MDH(1,1))         cos(MDH(1,1))            0                    0;
      0                     0                        1             MDH(1,2);
      0                     0                        0                   1];
 T12=[cos(MDH(2,1))         -sin(MDH(2,1))           0             MDH(2,3);
      0                     0                        1                    0;
      -sin(MDH(2,1))        -cos(MDH(2,1))           0                    0;
      0                     0                        0                   1];
 T23=[cos(MDH(3,1))         -sin(MDH(3,1))           0             MDH(3,3);
      sin(MDH(3,1))         cos(MDH(3,1))            0                    0;
      0                     0                        1                    0;
      0                     0                        0                   1];
 T34=[cos(MDH(4,1))         -sin(MDH(4,1))           0             MDH(4,3);
      0                     0                        1             MDH(4,2);
      -sin(MDH(4,1))        -cos(MDH(4,1))           0                    0
      0                     0                        0                   1];
 T45=[cos(MDH(5,1))         -sin(MDH(5,1))           0                    0;
      0                     0                        -1                   0;
      sin(MDH(5,1))         cos(MDH(5,1))            0                    0;
      0                     0                        0                   1];
 T56=[cos(MDH(6,1))         -sin(MDH(6,1))           0                    0;
      0                     0                        1                    0;
      -sin(MDH(6,1))        -cos(MDH(6,1))           0                    0;
      0                     0                        0                   1];
% 腕部到法兰
 T6TCP=[1                   0                        0                    0;
        0                   1                        0                    0;
        0                   0                        1                0.085;
        0                   0                        0                   1];
    
  T06=T01*T12*T23*T34*T45*T56*T6TCP;
  
  theta=[60*pi/180,-25*pi/180,40*pi/180,45*pi/180,-20*pi/180,60*pi/180];
%   [T06]=mymodfkine(theta)

       输入运行以上代码，然后命令行窗口输出注释行即可得到以下结果：

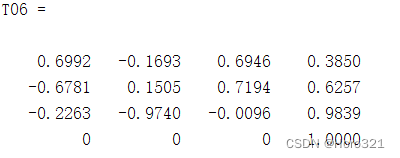
       由T06可以得到机器人末端的位置为（385，625.7，983.9），而姿态为以上旋转矩阵。在RobotStudio6.08中添加IRB2600型号机器人，各关节设置为（60°，-25°，40°，45°，-20°，60°），示教目标点后在机器人控制器中查看机器人当前位姿：

       控制器中机器人姿态采用欧拉角表示，而我们得到的结果为旋转矩阵，因此需要进行转换，可以自己写旋转矩阵转欧拉角公式：

R=[ -0.6992    0.1693    0.6946
    0.6781    -0.1505    0.7194    
    0.2263     0.9740   -0.0096 ];
 
r11=R(1,1);r12=R(1,2);r13=R(1,3);
r21=R(2,1);r22=R(2,2);r23=R(2,3);
r31=R(3,1);r32=R(3,2);r33=R(3,3);
 
Euler= [atan2(r21, r11); atan2(-r31, sqrt(r32 ^ 2 + r33 ^ 2)); atan2(r32, r33); ]*57.3

       也可以直接用matlab的转换函数rotm2eul(R)：

R=[0.6992    -0.1693    0.6946    
   -0.6781    0.1505    0.7194    
   -0.2263   -0.9740   -0.0096];
Euler=rotm2eul(R)*57.3

       得到结果为：

       可以看到在相同的关节角度下，求得的机器人末端位姿与官方数据一致，证明建立的MDH参数与正运动学方程准确无误。