波士顿房价预测_r语言波士顿房价数据可视化

利用R语言对波士顿房价数据做描述性分析和多元线性回归来预测波士顿房价：

A<-read.csv("E:/R语言练习/波士顿房价/housing.csv",head=T) 	#读取数据
dim(A)		#查看数据大小
1
2

506 14

Q=1;
for(i in 1:ncol(A)){Q[i]<-class(A[,i])}
Q;rm(Q);   	#查看每一列的数据类型，并且整理一下
1
2
3

CRIM “numeric” 人均犯罪率
ZN “numeric” 超过2W5平方英尺的住宅用地所占比例
INDUS “numeric” 城市非零售业的商业用地比例
CHAS “integer” Charles河是否流经
NOX “numeric” 一氧化碳浓度
RM “numeric” 每栋住宅的平均房间数
AGE “numeric” 1940年以前建成的自住房比例
DIS “numeric” 到波士顿五个中心区域的加权平均距离
RAD “integer” 到达高速公路的便利指数
TAX “numeric” 每1W美元的全值财产税率
PIRATIO “numeric” 师生比
B “numeric” BK是黑人比例，越接近0.63越小，B=1000*（BK-0.63）^2
LSTAT “numeric” 低收入人口比例
MEDV “numeric” 自住房屋房价的平均房价单位为（1W美元）

Q=1;
for(i in 1:ncol(A)){Q[i]<-sum(is.na(A[,i]));}
Q;		#查看每一列空值个数
1
2
3

描述性分析：

plot(CRIM,MEDV) #查看散点图和直方图
1

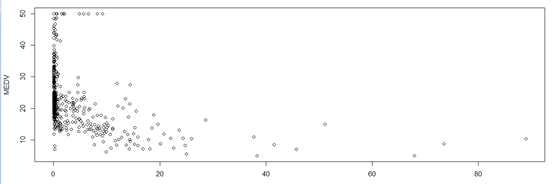
每个犯罪率对应的房价大概都呈正态分布，期望随着犯罪率的升高而降低，因为犯罪率越高，越没人敢住，自然没人买，房价就下降了，听说底特律最便宜的只要1美元。调查的地区大部分都在0附近，此处方差也比较大，波动较大，当CRIM>2时，方差比较稳定了。犯罪率在1~10之间的，地方还有几个地方房价很高，基本可以看作噪声。CRIM在25之后的地方数据量比较少。再查看直方图，发现332个地区都是犯罪率为0左右的。

plot(ZN,MEDV)  #查看散点图 
length(unique(ZN)); #计算ZN变量的取值种类数
1
2

[1] 26

tapply(MEDV,ZN,length);	#各种取值的平均值
1

0 12.5 17.5 18 20 21 22 25 28 30 33 34 35 40 45
372 10 1 1 21 4 10 10 3 6 4 3 3 7 6
52.5 55 60 70 75 80 82.5 85 90 95 100
3 3 4 3 3 15 2 2 5 4 1

lines(names(tapply(MEDV,ZN,mean)),as.numeric(tapply(MEDV,ZN,mean)));
1

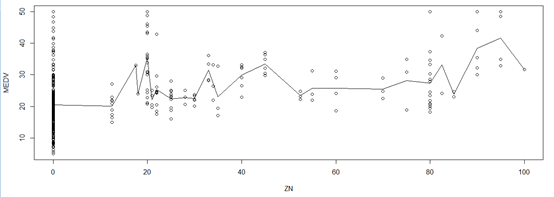
可以看到，大部分地区，豪宅都没有，房价在各个水平的变化基本都呈正态分布，且均值都相差不多，在85之后均值偏高，但数据量太小。所以基本可以认为此变量与房价没有关系

plot(INDUS,MEDV)
length(unique(INDUS)); #计算INDUS变量有几种取值
tapply(MEDV,INDUS,mean);	#各种取值的平均值
lines(names(tapply(MEDV,INDUS,mean)),as.numeric(tapply(MEDV,INDUS,mean)))#划线

1
2
3
4
5

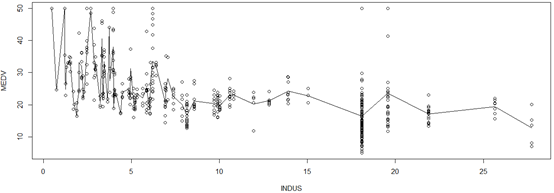
可以看到大部分人都居住在18左右的地区，在0~4之间房价变化没有明显的规律（对样本进行一次观测，小概率事件基本不会发生，但房价在上下反复横条，所以很难说有规律），但如果把INDUS值分个类，按区间进行划分，可以想象出来，在每个区间基本是正太分布的，而且期望随着INDUS增加而降低直到INDUS达到8，之后降低的幅度不太大，甚至有些平稳。

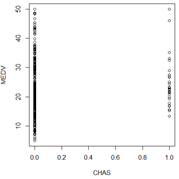
sum(CHAS==1)/length(CHAS);
1

[1] 0.06916996
大部分地区Charles河都没有流经，只有6.9%的地区被Charles经过

mean_test_double_normal(subset(A,A$CHAS==1)$MEDV,subset(A,A$CHAS==0)$MEDV);
1

假设他们的房价都服从正太分布，t检验一下，发现还是有差别的
mean df T P_value
1 6.346157 36.87641 3.113291 0.00356717

plot(NOX,MEDV)	#查看一氧化碳浓度与房价散点图
1

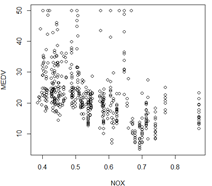
发现整体情况是随着一氧化碳浓度的升高，房价在降低，基本呈线性关系，0.7之后又有一些回升，不过不明显。

plot(RM,MEDV) #每栋住宅平均房间数
1

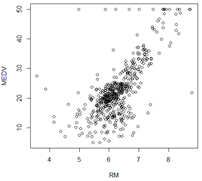
其实很符合常识，房间越多，占地越大，房子越贵，有一个点房子很多但很便宜，可能是犯罪率比较高的地方。

plot(AGE,MEDV)#查看老房子与房价关系
1

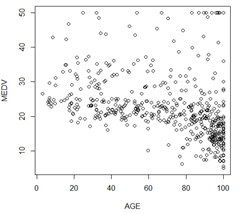
可以看出自住房在0~80差不多，影响不大，房价大部分都在20左右，在80以后呈下降趋势，这些地区基本全是老的自住房，因为没人愿意住，所以卖不出去，所以人就少，更加没人愿意来，恶性循环，所以房价非常低，通过前几张图可以看到价格在10以下的房子一氧化碳浓度也高，这图就展示了这些房子也是老的自住房，房间也少，不过都在河流旁边。还有一些地区全是是老的自住房，但是价格很高，应该是主人根本不想卖。 房价在每个水平都很像卡方分布。

plot(DIS,MEDV);  到5个市中心加权距离与房价关系
1

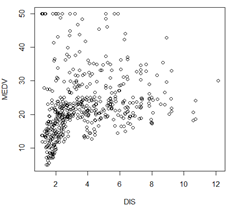
可以看出到市中心越近，越便宜，均值越低，距离3之后逐渐平稳，可能是因为波士顿的人都比较喜欢住在郊区，我们又看到，价格在10以下的距离市中心也很近，说明波士顿的城市规划可能不太好，因为一般来讲商业区人流量比较多，房价都很高，而它的市中心都是老的自住房，怪不得经济没有纽约等城市好。

plot(RAD,MEDV); #到高速公路的距离与房价的关系
1

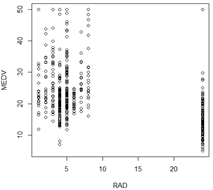
可以看到一大半地区距离高速都挺近的，房价差距不大，有一小半是非常远的 ，这部分地区的房子房价就很便宜，只有一个是很贵的，基本都比左边的要便宜，包括之前说到的在市中心的便宜的老房子，犯罪率也高。

plot(TAX,MEDV); #税与房价关系
1

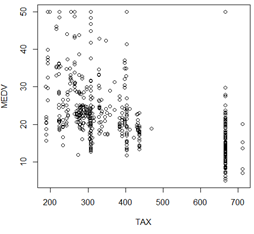
mean_test_double_normal(subset(A,A$TAX<500)$MEDV,subset(A,A$TAX>500)$MEDV);
1

mean df T P_value
1 8.584919 240.4148 10.1814 0
税很高的地区，基本没有房价很高的，税很少的地区各种房价都有，不过大部分都比较低，但均值还是比税高的地方要高，各个水平房价也有点像卡方分布。

plot(PIRATIO,MEDV) 	#师生比与房价关系
1

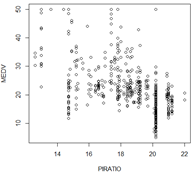
师生比越高，房价越低，但是在中间部分不太明显，主要是因为在14.5时这几个数据太低了，整体是递减的

plot(B,MEDV) 	#黑人比例与房价关系
1

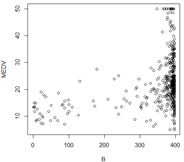
黑人比较少的地方，房价都比较低，黑人比较多的地方，每个水平房价基本都呈正太分布

mean_test_double_normal(subset(A,A$B<=200)$MEDV,subset(A,A$B>200)$MEDV);
1

   mean       df         T     P_value
1

1 -10.19277 70.17524 -12.58664 1.14343e-19
因为中间部分人比较少，而且200以前的分布相似，200以后的分布相似，所以给数据分成两部分进行T检验，结果显著，说明有明显差别

plot(LSTAT,MEDV) #低收入人口比例与房价的关系
1

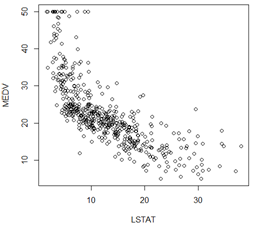
可以看出，人均收入越低的地方房价越低，与常识相符，又是一个恶性循环。

回归分析：

Split=0.8;
AA1<-A[1:spilt*nrow(A1),];		#训练集
AA2<-A[(split*nrow(A1)+1):nrow(A1),1:(ncol(A)-1)];		#测试集
1
2
3

多元线性回归：

A1<-AA1  #不破坏源数据，在A1中分析
C1<-lm(MEDV~.,data=A1);  #现对原始数据进行线性回归
summary(C1);
1
2
3
4

Call:
lm(formula = MEDV ~ ., data = A1)

Residuals:
Min 1Q Median 3Q Max
-19.9717 -2.7981 -0.6206 1.5642 25.3066

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.077167 6.196821 4.854 1.76e-06 ***
CRIM -0.202135 0.053695 -3.764 0.000193 ***
ZN 0.044128 0.014257 3.095 0.002109 **
INDUS 0.052674 0.066204 0.796 0.426729
CHAS 1.884743 0.898988 2.097 0.036680 *
NOX -14.928149 4.604692 -3.242 0.001289 **
RM 4.760387 0.486625 9.782 < 2e-16 ***
AGE 0.002887 0.014474 0.199 0.841983
DIS -1.300253 0.213913 -6.078 2.89e-09 ***
RAD 0.461662 0.087944 5.249 2.51e-07 ***
TAX -0.015543 0.004493 -3.460 0.000601 ***
PIRATIO -0.811632 0.141526 -5.735 1.96e-08 ***
B -0.001972 0.006597 -0.299 0.765179
LSTAT -0.532273 0.059777 -8.904 < 2e-16 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.858 on 390 degrees of freedom
Multiple R-squared: 0.7338, Adjusted R-squared: 0.7249
F-statistic: 82.68 on 13 and 390 DF, p-value: < 2.2e-16

deviance(C1) #查看残差平方和
1

[1] 9202.465

XX<-cor(A1[,1:(ncol(A1)-1)])
1

kappa(XX);
1

[1] 36.97902
可以看到对方程的F检验通过了，有三个自变量没有通过t检验,分别是INDUS、AGE和B，与我们描述性分析基本一致，AGE是在80以后才有一点小的变化；INDUS是前面整体比后面整体要大，但是前面整体内部变化情况较乱，后面整体内部基本变化不明显；B是黑人比例，也是变化不大，不过左右两侧作为整体有些变化。残差的标准差是4.858，复相关系数0.7338，不高，说明解释性不强。ZN的系数通过了检验，这与我们描述性分析结论有点区别。残差平方和为9202.465。矩阵条件数<100说明共线性不强。
现在对数据进行一些处理：

在假定三个不显著的变量都是正态的前提下，我们对其元素分类。
#对INDUS分区间贴标签,每2.5分一次

for(i in 1:12){A1[,3][A1[,3]>=(i-1)*2.5&A1[,3]<i*2.5]=i;}
1

#对AGE贴标签80以前为一组，80以后为一组

A1[,7][A1[,7]<=80]=1;
A1[,7][A1[,7]>80]=0;
1
2

#对B贴标签，200以前为一组，200以后为一组

A1[,12][A1[,12]<=200]=1;
A1[,12][A1[,12]>200]=0;
1
2

#再进行一次回归
Call:
lm(formula = MEDV ~ ., data = A1)

Residuals:
Min 1Q Median 3Q Max
-19.8383 -2.5920 -0.5508 1.5936 24.8959

Coefficients:

         Estimate Std. Error t value Pr(>|t|)    
1

(Intercept) 31.575224 6.032988 5.234 2.72e-07 ***
CRIM -0.198901 0.053555 -3.714 0.000234 ***
ZN 0.043376 0.014132 3.069 0.002295 **
INDUS 0.103983 0.163501 0.636 0.525165
CHAS 1.872050 0.897298 2.086 0.037599 *
NOX -15.239462 4.567486 -3.337 0.000930 ***
RM 4.632372 0.481343 9.624 < 2e-16 ***
AGE -0.872492 0.780957 -1.117 0.264593
DIS -1.269598 0.207450 -6.120 2.28e-09 ***
RAD 0.460565 0.086853 5.303 1.91e-07 ***
TAX -0.015873 0.004493 -3.533 0.000461 ***
PIRATIO -0.828216 0.141281 -5.862 9.74e-09 ***
B -0.801184 2.111246 -0.379 0.704535
LSTAT -0.550811 0.058171 -9.469 < 2e-16 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.85 on 390 degrees of freedom
Multiple R-squared: 0.7346, Adjusted R-squared: 0.7257
F-statistic: 83.03 on 13 and 390 DF, p-value: < 2.2e-16

deviance(C11)
1

[1] 9174.004
方程通过F检验，他们三个还是没有通过检验 ，残差标准差和平方和降低，复相关系数增加，说明模型更好了
所以现在把这三个变量去掉

A1<-A1[,-12];
A1<-A1[,-7];
A1<-A1[,-3];#从后往前，以免打乱数据，删错列。
C12<-lm(MEDV~.,data=A1)  #再进行回归
1
2
3
4

summary(C12)
1

Call:
lm(formula = MEDV ~ ., data = A1)

Residuals:
Min 1Q Median 3Q Max
-19.8616 -2.6420 -0.6481 1.6850 25.5133

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.867718 5.591716 5.163 3.88e-07 ***
CRIM -0.201792 0.053391 -3.780 0.000181 ***
ZN 0.042993 0.014057 3.058 0.002377 **
CHAS 1.981299 0.889328 2.228 0.026455 *
NOX -13.251201 4.078561 -3.249 0.001258 **
RM 4.723181 0.465942 10.137 < 2e-16 ***
DIS -1.345058 0.199372 -6.746 5.44e-11 ***
RAD 0.440431 0.084196 5.231 2.75e-07 ***
TAX -0.014306 0.004248 -3.367 0.000834 ***
PIRATIO -0.794205 0.138502 -5.734 1.96e-08 ***
LSTAT -0.525396 0.055047 -9.545 < 2e-16 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.844 on 393 degrees of freedom
Multiple R-squared: 0.7332, Adjusted R-squared: 0.7264
F-statistic: 108 on 10 and 393 DF, p-value: < 2.2e-16

 deviance(C12)
1

[1] 9220.609
可以看到F增大了，所有系数都通过检验，很不错，不过复相关系数降低了，残差标准差，平方和也升高了，这个不太好，而且ZN还是显著的，跟描述性分析不符。
进一步作回归诊断，看看是不是异常值的原因

Reg_Diag(C12);
1

结果不展示了，太长了

w<-c(142,162,163,167,187,215,254,365,366,368,369,370,371,372,373,375,376,381,402)
1

将异常值的横坐标给w

A1<-A1[-w,];  #从A1中删除异常统计量在3个以上的数据
dim(A1)  #查看A1行列数
1
2

[1] 385 11

C13<-lm(MEDV~.,data=A1)
summary(C13)
deviance(C13)
1
2
3

Call:
lm(formula = MEDV ~ ., data = A1)

Residuals:
Min 1Q Median 3Q Max
-7.9670 -2.1510 -0.1886 1.6156 10.6536

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.735197 4.242986 1.352 0.177292
CRIM -0.175195 0.069440 -2.523 0.012051 *
ZN 0.036690 0.009703 3.781 0.000182 ***
CHAS 0.934701 0.641074 1.458 0.145674
NOX -5.604788 2.821799 -1.986 0.047736 *
RM 6.901025 0.373911 18.456 < 2e-16 ***
DIS -0.786486 0.141392 -5.562 5.08e-08 ***
RAD 0.296209 0.064603 4.585 6.20e-06 ***
TAX -0.018215 0.002937 -6.203 1.47e-09 ***
PIRATIO -0.672052 0.095317 -7.051 8.65e-12 ***
LSTAT -0.292189 0.044109 -6.624 1.22e-10 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.271 on 374 degrees of freedom
Multiple R-squared: 0.8536, Adjusted R-squared: 0.8497
F-statistic: 218.1 on 10 and 374 DF, p-value: < 2.2e-16

 deviance(C13)
1

[1] 4001.539
可以看到F值增加了100，复相关系数增加到0.8536，残差标准差降到3.271，删除了29个数据，可是残差平方和降低了一半多，降到4001.539，可见异常值的影响是很大的。从结果中可以看到CHAS和常数没有通过检验。现在将CHAS去掉看看

A1[1:2,]
1

CRIM ZN CHAS NOX RM DIS RAD TAX PIRATIO LSTAT MEDV
1 0.00632 18 0 0.538 6.575 4.0900 1 296 15.3 4.98 24.0
2 0.02731 0 0 0.469 6.421 4.9671 2 242 17.8 9.14 21.6
看到CHAS在第三列，千万别删错了，因为之前删过数据，所以很多数据的索引发生了变化

A1<-A1[,-3];
C14<-lm(MEDV~.,data=A1)
summary(C14)
1
2
3

Call:
lm(formula = MEDV ~ ., data = A1)

Residuals:
Min 1Q Median 3Q Max
-8.1056 -2.1554 -0.1984 1.6563 10.4840

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.840944 4.248729 1.375 0.170030
CRIM -0.186437 0.069114 -2.698 0.007301 **
ZN 0.036821 0.009717 3.789 0.000176 ***
NOX -5.316536 2.819087 -1.886 0.060080 .
RM 6.916277 0.374325 18.477 < 2e-16 ***
DIS -0.794414 0.141500 -5.614 3.85e-08 ***
RAD 0.308874 0.064112 4.818 2.11e-06 ***
TAX -0.018642 0.002927 -6.370 5.54e-10 ***
PIRATIO -0.683071 0.095159 -7.178 3.82e-12 ***
LSTAT -0.289376 0.044133 -6.557 1.82e-10 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.276 on 375 degrees of freedom
Multiple R-squared: 0.8528, Adjusted R-squared: 0.8493
F-statistic: 241.4 on 9 and 375 DF, p-value: < 2.2e-16

 deviance(C14)
1

[1] 4024.283
可以看到除了F值，各项不如原来的好，不过相差不多，但常数项没通过检验，可能是因为有些不是正态分布的变量影响比较大,NOX值也点低，删掉NOX试试

A1<-A1[,-3];
 C15<-lm(MEDV~.,data=A1)
 summary(C15)
1
2
3

Call:
lm(formula = MEDV ~ ., data = A1)

Residuals:
Min 1Q Median 3Q Max
-7.9141 -2.2969 -0.0911 1.6559 10.5162

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.375361 3.539705 0.389 0.6978
CRIM -0.173393 0.069000 -2.513 0.0124 *
ZN 0.038434 0.009712 3.957 9.06e-05 ***
RM 7.016687 0.371777 18.873 < 2e-16 ***
DIS -0.655955 0.121374 -5.404 1.16e-07 ***
RAD 0.300155 0.064162 4.678 4.05e-06 ***
TAX -0.020228 0.002813 -7.192 3.48e-12 ***
PIRATIO -0.617640 0.088910 -6.947 1.65e-11 ***
LSTAT -0.305740 0.043418 -7.042 9.08e-12 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.287 on 376 degrees of freedom
Multiple R-squared: 0.8514, Adjusted R-squared: 0.8482
F-statistic: 269.3 on 8 and 376 DF, p-value: < 2.2e-16

 deviance(C15)
1

[1] 4062.451
除了F，其他指标都不如之前，不过变化也不大，可以接受，整体来看还是更好了。
#最优的线性回归模型为
MEDV=1.38-0.17CRIM+0.04ZN+7.02RM-0.66DIS+0.3RAD-0.02TAX
-0.62PIRATIO-0.31LSTAT

#，画图，先要对数据进行处理，主要是分区，但是我们最终的模型没有变量是分区的，所以可以不做

A1.pre<-predict(C15,AA2)
plot(as.numeric(A1.pre)~names(A1.pre),pch=16,col="red",cex=1,main="预测结果")#cex表示散点的大小
points(names(A1.pre),A[(floor(split*nrow(A))+1):nrow(A),ncol(A)],pch=17,col="blue",cex=1)
lines(names(A1.pre),as.numeric(A1.pre),col='red',)
lines(names(A1.pre),A[(floor(split*nrow(A))+1):nrow(A),ncol(A)],col='blue')
legend(500,0,c("预测","实际"),col=c("red","blue"),text.col=c("red","blue"))
1
2
3
4
5
6

现在做非线性回归：

#通过观察散点图，我们假设
#MEDV和DIS是对数关系，和NOX是反比，和LSTAT是反比关系

A2<-AA1;
1

#先把LSTAT加进去

C2<-nls(MEDV~a*CRIM+b*ZN+c*INDUS+d*CHAS+e*NOX+f*RM+g*RAD+h*TAX+i*PIRATIO+j*B
+k*AGE+m*DIS+n/LSTAT+o,data=A2,
start=list(a=1,b=1,c=1,d=1,e=1,f=1,g=1,h=1,i=1,j=1,k=1,m=1,n=1,o=1));
summary(C2)
1
2
3
4

Formula: MEDV ~ a * CRIM + b * ZN + c * INDUS + d * CHAS + e * NOX + f *
RM + g * RAD + h * TAX + i * PIRATIO + j * B + k * AGE +
m * DIS + n/LSTAT + o

Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.251005 0.047539 -5.280 2.15e-07 ***
b 0.011775 0.013061 0.902 0.367878
c -0.047643 0.059941 -0.795 0.427192
d 1.512187 0.817223 1.850 0.065013 .
e -14.427150 4.177197 -3.454 0.000613 ***
f 3.827466 0.443403 8.632 < 2e-16 ***
g 0.394948 0.080055 4.933 1.20e-06 ***
h -0.013708 0.004075 -3.364 0.000844 ***
i -0.746102 0.128686 -5.798 1.39e-08 ***
j -0.004173 0.005973 -0.699 0.485238
k 0.007627 0.012828 0.595 0.552461
m -1.087038 0.195336 -5.565 4.88e-08 ***
n 55.142256 4.118554 13.389 < 2e-16 ***
o 22.575740 5.470289 4.127 4.50e-05 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.41 on 390 degrees of freedom

Number of iterations to convergence: 2
Achieved convergence tolerance: 1.064e-07

deviance(C2)
1

[1] 7586.345
发现bcdjk都不是很显著，b从散点图看就不相关，不处理，其他的变量变换后再回归：

#对INDUS分区间贴标签,每2.5分一次
for(i in 1:12){
A2[,3][(A2[,3]>=(i-1)*2.5)&(A2[,3]<i*2.5)]=i;
}
table(A2[,3])
#对AGE贴标签80以前为一组，80以后为一组
A2[,7][A2[,7]<=80]=1;
A2[,7][A2[,7]>80]=0;
#对B贴标签，200以前为一组，200以后为一组
A2[,12][A2[,12]<=200]=1;
A2[,12][A2[,12]>200]=0;
C21<-nls(MEDV~a*CRIM+b*ZN+c*INDUS+d*CHAS+e*NOX+f*RM+g*RAD+h*TAX+i*PIRATIO+j*B
+k*AGE+m*DIS+n/LSTAT+o,data=A2,
start=list(a=1,b=1,c=1,d=1,e=1,f=1,g=1,h=1,i=1,j=1,k=1,m=1,n=1,o=1));
summary(C21)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Formula: MEDV ~ a * CRIM + b * ZN + c * INDUS + d * CHAS + e * NOX + f *
RM + g * RAD + h * TAX + i * PIRATIO + j * B + k * AGE +
m * DIS + n/LSTAT + o

Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.252106 0.047559 -5.301 1.93e-07 ***
b 0.010767 0.013075 0.823 0.410752
c -0.125932 0.148607 -0.847 0.397285
d 1.535027 0.817367 1.878 0.061125 .
e -13.648770 4.158405 -3.282 0.001123 **
f 3.811601 0.438272 8.697 < 2e-16 ***
g 0.390309 0.079196 4.928 1.23e-06 ***
h -0.013572 0.004078 -3.328 0.000958 ***
i -0.750662 0.128827 -5.827 1.18e-08 ***
j -0.320530 1.917126 -0.167 0.867305
k -0.321838 0.689789 -0.467 0.641065
m -1.097824 0.189142 -5.804 1.34e-08 ***
n 54.787903 3.982917 13.756 < 2e-16 ***
o 21.620453 5.175028 4.178 3.63e-05 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.414 on 390 degrees of freedom

Number of iterations to convergence: 1
Achieved convergence tolerance: 4.263e-06

deviance(C21) 
1

[1] 7597.095
发现还是不显著， 残差平方和还变大了，删掉再回归

C22<-nls(MEDV~a*CRIM+e*NOX+f*RM+g*RAD+h*TAX+i*PIRATIO+m*DIS+n/LSTAT+o,data=A2,
start=list(a=1,e=1,f=1,g=1,h=1,i=1,m=1,n=1,o=1));
summary(C22)
1
2
3

Formula: MEDV ~ a * CRIM + e * NOX + f * RM + g * RAD + h * TAX + i *
PIRATIO + m * DIS + n/LSTAT + o

Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.260031 0.047128 -5.518 6.23e-08 ***
e -13.946205 3.634807 -3.837 0.000145 ***
f 3.956861 0.425057 9.309 < 2e-16 ***
g 0.414774 0.076104 5.450 8.88e-08 ***
h -0.014190 0.003789 -3.745 0.000208 ***
i -0.810321 0.119160 -6.800 3.87e-11 ***
m -1.017899 0.157999 -6.442 3.42e-10 ***
n 55.353782 3.855677 14.356 < 2e-16 ***
o 21.147236 4.902498 4.314 2.03e-05 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.413 on 395 degrees of freedom

Number of iterations to convergence: 1
Achieved convergence tolerance: 3.627e-06

deviance(C22)
1

[1] 7693.275
剩余的变量都通过检验，不过残差平方和还是变大了
#NOX变成反比再回归 发现效果不如原来

C23<-nls(MEDV~a*CRIM+e/NOX+f*RM+g*RAD+h*TAX+i*PIRATIO+m*DIS+n/LSTAT+o,data=A2,
start=list(a=1,e=10,f=1,g=1,h=1,i=1,m=1,n=1,o=1));
summary(C23)
1
2
3

Formula: MEDV ~ a * CRIM + e/NOX + f * RM + g * RAD + h * TAX + i * PIRATIO +
m * DIS + n/LSTAT + o

Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.260564 0.047339 -5.504 6.69e-08 ***
e 4.363338 1.292939 3.375 0.000812 ***
f 4.052570 0.424388 9.549 < 2e-16 ***
g 0.421321 0.076530 5.505 6.65e-08 ***
h -0.015552 0.003738 -4.161 3.90e-05 ***
i -0.735695 0.115047 -6.395 4.55e-10 ***
m -1.084244 0.182984 -5.925 6.79e-09 ***
n 55.164736 3.897510 14.154 < 2e-16 ***
o 3.983916 4.046109 0.985 0.325409

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.431 on 395 degrees of freedom

Number of iterations to convergence: 1
Achieved convergence tolerance: 3.822e-06

 deviance(C23)
1

[1] 7756.362
效果还不如原来的

#把DIS设成对数形式

C24<-nls(MEDV~a*CRIM-e*NOX+f*RM+g*RAD+h*TAX+i*PIRATIO+m*log(DIS)+n/LSTAT+o,data=A2,
start=list(a=1,e=1,f=1,g=1,h=1,i=1,m=1,n=1,o=1));
summary(C24)
1
2
3

Formula: MEDV ~ a * CRIM - e * NOX + f * RM + g * RAD + h * TAX + i *
PIRATIO + m * log(DIS) + n/LSTAT + o

Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.288912 0.046263 -6.245 1.10e-09 ***
e 21.114324 3.889389 5.429 9.93e-08 ***
f 3.948924 0.413100 9.559 < 2e-16 ***
g 0.422674 0.074201 5.696 2.39e-08 ***
h -0.016805 0.003683 -4.563 6.73e-06 ***
i -0.805920 0.115688 -6.966 1.37e-11 ***
m -5.929153 0.742749 -7.983 1.57e-14 ***
n 54.652676 3.756986 14.547 < 2e-16 ***
o 29.318120 5.117149 5.729 2.00e-08 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.305 on 395 degrees of freedom

Number of iterations to convergence: 1
Achieved convergence tolerance: 5.366e-06

deviance(C24)
1

[1] 7320.632
残差平方和小了300，还不错，而且都通过检验，但是残差平方和还是不够小(跟线性回归相比) 但是又不能进行回归诊断，所以就删掉线性回归时诊断出的异常值，再进行一次回归
试一试，万一效果更好了呢

C25<-nls(MEDV~a*CRIM-e*NOX+f*RM+g*RAD+h*TAX+i*PIRATIO+m*log(DIS)+n/LSTAT+o,data=A2,
start=list(a=1,e=1,f=1,g=1,h=1,i=1,m=1,n=1,o=1));
summary(C25)
1
2
3

Formula: MEDV ~ a * CRIM - e * NOX + f * RM + g * RAD + h * TAX + i *
PIRATIO + m * log(DIS) + n/LSTAT + o

Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.347812 0.061977 -5.612 3.89e-08 ***
e 9.278565 2.896132 3.204 0.00147 **
f 6.045485 0.362698 16.668 < 2e-16 ***
g 0.315196 0.059630 5.286 2.13e-07 ***
h -0.016665 0.002659 -6.267 1.01e-09 ***
i -0.732264 0.083813 -8.737 < 2e-16 ***
m -3.127534 0.574620 -5.443 9.48e-08 ***
n 36.901873 3.335820 11.062 < 2e-16 ***
o 7.352548 4.132847 1.779 0.07604 .

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.054 on 376 degrees of freedom

Number of iterations to convergence: 1
Achieved convergence tolerance: 2.7e-06

deviance(C25)  
1

[1] 3507.183
效果确实好了不少，直接降到3500，但是常数项不是很显著
所以最终模型就是
MEDV=-0.35CRIM+9.27NOX+6.05RM+0.32RAD-0.017TAX
-0.73PIRATIO-3.13*log(DIS)+36.9/LSTAT+7.35

现在把因变量取对数再回归：

A3<-AA1;
A3[,14]<-log(A3[,14])
C3<-lm(MEDV~.,data=A3)
summary(C3)
deviance(C3)
XX<-cor(A3[,1:(ncol(A3)-1)])
kappa(XX);
1
2
3
4
5
6
7

Call:
lm(formula = MEDV ~ ., data = A3)

Residuals:
Min 1Q Median 3Q Max
-0.72855 -0.09231 -0.00923 0.08615 0.80584

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.778e+00 2.309e-01 16.362 < 2e-16 ***
CRIM -1.292e-02 2.001e-03 -6.457 3.19e-10 ***
ZN 1.227e-03 5.313e-04 2.309 0.021444 *
INDUS 2.437e-03 2.467e-03 0.988 0.323926
CHAS 9.024e-02 3.350e-02 2.694 0.007370 **
NOX -5.816e-01 1.716e-01 -3.389 0.000772 ***
RM 1.260e-01 1.813e-02 6.950 1.54e-11 ***
AGE 1.384e-04 5.394e-04 0.257 0.797684
DIS -4.413e-02 7.972e-03 -5.536 5.69e-08 ***
RAD 1.384e-02 3.277e-03 4.223 3.00e-05 ***
TAX -6.259e-04 1.674e-04 -3.738 0.000213 ***
PIRATIO -3.126e-02 5.274e-03 -5.926 6.82e-09 ***
B 1.806e-05 2.458e-04 0.073 0.941483
LSTAT -2.795e-02 2.228e-03 -12.545 < 2e-16 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.181 on 390 degrees of freedom
Multiple R-squared: 0.7819, Adjusted R-squared: 0.7747
F-statistic: 107.6 on 13 and 390 DF, p-value: < 2.2e-16
发现结论与线性回归相似，还是这几个量不显著

deviance(C3)
1

[1] 12.77962
残差平方和为12.78

kappa(XX);
1

[1] 36.97902
共线性较弱
删除不显著变量

A3<-A3[,-12];
A3<-A3[,-7];
A3<-A3[,-3];
C31<-lm(MEDV~.,data=A3)
summary(C31)
deviance(C31)
1
2
3
4
5
6

Call:
lm(formula = MEDV ~ ., data = A3)

Residuals:
Min 1Q Median 3Q Max
-0.72678 -0.09215 -0.01038 0.08291 0.81418

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.7644196 0.2084477 18.059 < 2e-16 ***
CRIM -0.0129072 0.0019903 -6.485 2.67e-10 ***
ZN 0.0011736 0.0005240 2.240 0.025668 *
CHAS 0.0944176 0.0331523 2.848 0.004631 **
NOX -0.5212456 0.1520404 -3.428 0.000672 ***
RM 0.1254235 0.0173694 7.221 2.69e-12 ***
DIS -0.0463659 0.0074322 -6.239 1.14e-09 ***
RAD 0.0130698 0.0031387 4.164 3.84e-05 ***
TAX -0.0005750 0.0001584 -3.631 0.000320 ***
PIRATIO -0.0303039 0.0051631 -5.869 9.31e-09 ***
LSTAT -0.0275465 0.0020520 -13.424 < 2e-16 ***

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1806 on 393 degrees of freedom
Multiple R-squared: 0.7813, Adjusted R-squared: 0.7758
F-statistic: 140.4 on 10 and 393 DF, p-value: < 2.2e-16
都通过检验

deviance(C31)
[1] 12.81337
Reg_Diag(C31)

#异常数据：

w1<-c(8,142,149,215,365,366,368,369,370,371,372,393,374,375,381,398,399,400,401,402)
A3<-A3[-w1,] #删掉异常值再回归
C32<-lm(MEDV~.,data=A3)
summary(C32)
deviance(C32)
1
2
3
4
5

Call:
lm(formula = MEDV ~ ., data = A3)

Residuals:
Min 1Q Median 3Q Max
-0.34815 -0.08112 -0.00769 0.06909 0.86829

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.9142258 0.1612867 18.069 < 2e-16 ***
CRIM -0.0212239 0.0033019 -6.428 3.96e-10 ***
ZN 0.0008903 0.0003751 2.374 0.018112 *
CHAS 0.0862206 0.0243773 3.537 0.000456 ***
NOX -0.3166183 0.1111940 -2.847 0.004651 **
RM 0.2081295 0.0140476 14.816 < 2e-16 ***
DIS -0.0318698 0.0054444 -5.854 1.05e-08 ***
RAD 0.0134964 0.0026161 5.159 4.04e-07 ***
TAX -0.0005620 0.0001130 -4.975 9.99e-07 ***
PIRATIO -0.0257613 0.0037241 -6.918 2.01e-11 ***
LSTAT -0.0209177 0.0017551 -11.918 < 2e-16 ***

---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1275 on 373 degrees of freedom
Multiple R-squared: 0.8674, Adjusted R-squared: 0.8639
F-statistic: 244.1 on 10 and 373 DF, p-value: < 2.2e-16

 deviance(C32)
1

[1] 6.066216
残差平方和降低一半，复相关系数增加到0.8674比线性回归要好一些。

#所以最终模型为
MEDV=exp(2.91-0.02CRIM+0.00089ZN+0.086CHAS-0.32NOX
+0.21RM-0.032DIS+0.0135RAD-0.00056TAX-0.026PIRATIO-0.021LSTAT)

可以看到 第三种波动比较小，而且没有预测值在0以下，前两种都有，所以我选择第三种模型
做的过程中有很多不足之处，比如有些不是正态分布的，或者异方差的，还有有些参数跟散点图描绘的不一样比如DIS，但是删掉后效果更差，我没放上来给你们看，有什么想法就提出来吧，我也是个新手，一起讨论。