devbox
繁依Fanyi0
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【数据结构（C语言）】排序详解

作者：繁依Fanyi0 | 2024-02-29 04:57:19

赞

踩

【数据结构（C语言）】排序详解

目录

文章目录

前言

一、排序的概念

1.1  排序的概念

1.2 常见的排序算法

二、插入排序

2.1 直接插入排序

2.1.1 基本思想 

2.1.2 特性总结

2.1.3 代码实现

2.2 希尔排序

2.2.1 基本思想 

2.2.2 特性总结

2.2.3 代码实现

三、选择排序

3.1 直接选择排序

3.1.1 基本思想

3.1.2 特性总结

3.1.3 代码实现

3.2 堆排序

3.2.1 基本思想

3.2.2 特性总结

3.2.3 代码实现

四、交换排序

4.1 冒泡排序

4.1.1 基本思想

4.1.2 特性总结

4.1.3 代码实现

4.2 快速排序

4.2.1 基本思想

4.2.2 特性总结

4.2.3 代码实现

五、归并排序

5.1 归并排序

5.1.1 基本思想

5.1.2 特征总结

5.1.3 代码实现

六、计数排序

6.1 计数排序

6.1.1  基本思想

6.1.2 特征总结

6.1.3 代码实现

七、排序比较

总结

前言

在当今信息爆炸的时代，数据量不断攀升，排序算法作为处理数据的核心技术，其在计算机科学、大数据、人工智能等领域的重要性不言而喻。本文旨在介绍各种排序算法，帮助读者掌握其原理、特点及适用场景，从而提高数据处理效率，提升系统性能。

本文将详细介绍常见的排序算法，包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等，并分析各种排序算法的时间复杂度、空间复杂度和稳定性，让你在实际应用中能够灵活选择合适的排序方法。

一、排序的概念

1.1  排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

内部排序：数据元素全部放在内存中的排序。

外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

1.2 常见的排序算法

二、插入排序

2.1 直接插入排序

2.1.1 基本思想 

直接插入排序（Insertion Sort）是一种简单直观的排序算法。它的基本思想是将待排序的序列分为已排序和未排序两部分，在每一趟排序中，从未排序的部分中选择一个元素，然后将其插入到已排序的部分中的正确位置，直到所有元素都被插入到已排序的部分中。

具体的步骤如下：

  1. 将序列的第一个元素看作已排序的部分，剩余部分看作未排序的部分。
  2. 从未排序的部分中选取一个元素，依次与已排序的部分中的元素进行比较，找到合适的位置插入。
  3. 插入元素时，需要将已排序的部分中比插入元素大的元素依次向后移动一个位置，给插入元素腾出位置。
  4. 重复步骤2和步骤3，直到所有元素都插入到已排序的部分中。

直接插入排序的时间复杂度为O(n^2)，其中n为待排序序列的长度。它是稳定的排序算法，适用于小规模的数据或基本有序的数据。在实际应用中，当待排序序列规模较小或已经基本有序时，直接插入排序是一个简单有效的选择。

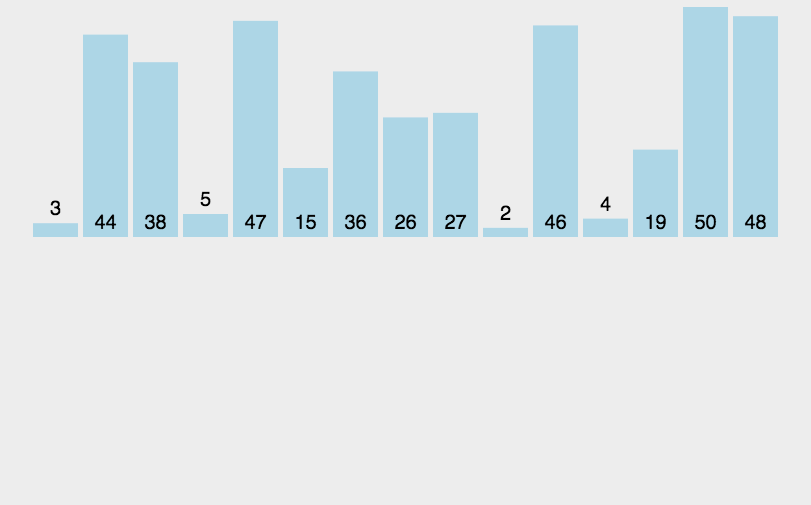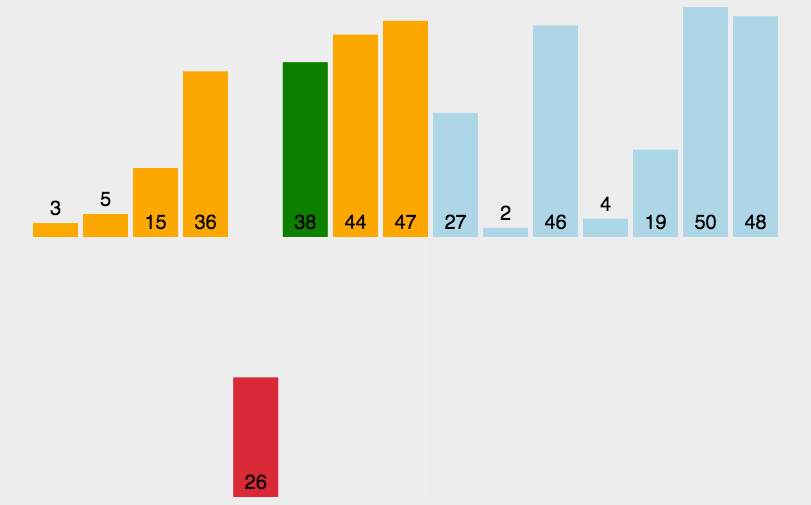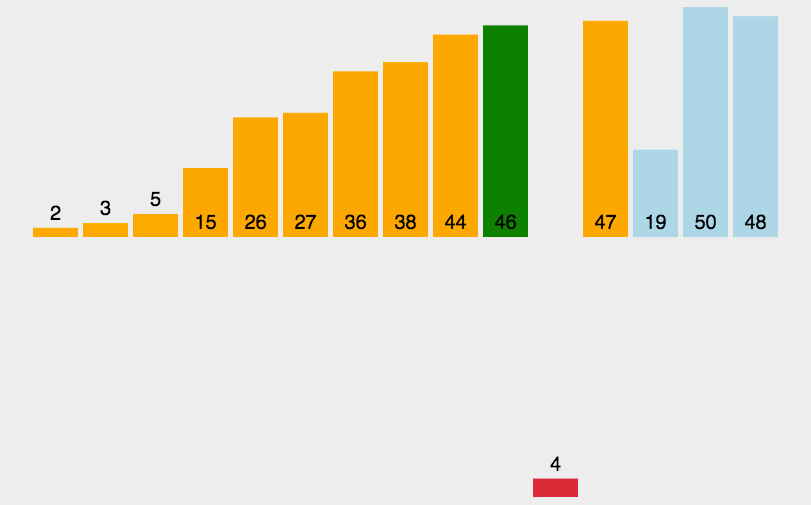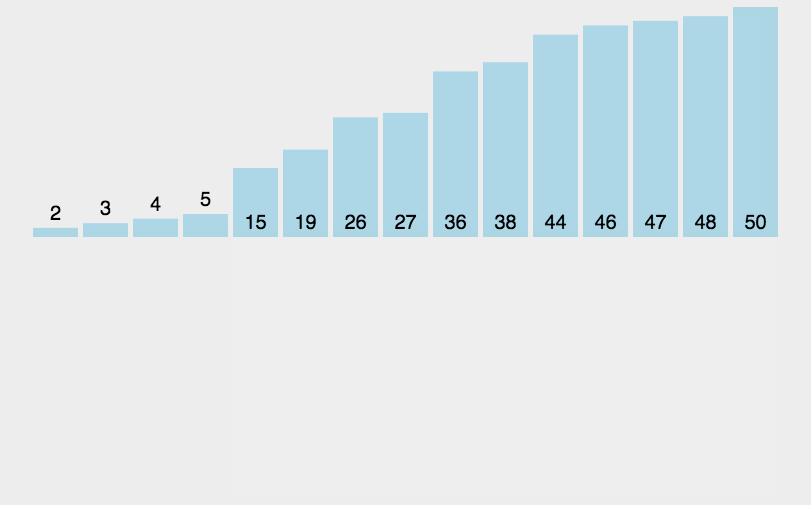
2.1.2 特性总结

  1. 元素集合越接近有序，直接插入排序算法的时间效率越高
  2. 时间复杂度：O(N^2)
  3. 空间复杂度：O(1)，它是一种稳定的排序算法
  4. 稳定性：稳定 

2.1.3 代码实现

  1. void InsertSort(int* a, int n)
  2. {
  3. 	for (int i = 0; i < n - 1; i++)
  4. 	{
  5. 		int end = i;
  6. 		int tmp = a[end + 1];
  7. 		while (end >= 0)
  8. 		{
  9. 			if (a[end] > tmp)
  10. 			{
  11. 				a[end + 1] = a[end];
  12. 				end--;
  13. 			}
  14. 			else
  15. 			{
  16. 				break;
  17. 			}
  18.  
  19. 		}
  20. 		a[end + 1] = tmp;
  21. 	}
  22. }

2.2 希尔排序

2.2.1 基本思想 

希尔排序是一种排序算法，通过将待排序的数组分割成若干个子序列进行插入排序，从而达到整体有序的目的。它是插入排序的改进版，也被称为缩小增量排序。

希尔排序的基本思想是：对数组进行分组，按一定的间隔（增量）将元素分为若干个子序列，对每个子序列进行插入排序，然后减小增量再次分组并排序，直到增量为1时，进行最后的插入排序。

具体的步骤如下：

  1. 选择一个增量序列，通常初始增量为数组长度的一半，之后依次减半，直到增量为1。
  2. 对于每个增量，将数组分成若干个长度为增量的子序列。
  3. 对每个子序列进行插入排序。
  4. 缩小增量，重复步骤2和3，直到增量为1。
  5. 最后进行一次插入排序，完成排序。

希尔排序的时间复杂度和增量序列的选择有关，但最坏时间复杂度为O(n^2)，平均时间复杂度为O(n^1.3)。相比于插入排序的O(n^2)时间复杂度，希尔排序有较好的性能。

希尔排序是一种原地排序算法，不需要额外的空间，因此它的空间复杂度为O(1)。但它不稳定，相同元素可能会被交换位置，因此对于有重复元素的数组，可能需要考虑其他的排序算法。

2.2.2 特性总结

1. 希尔排序是对直接插入排序的优化。

2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。

3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些书中给出的希尔排序的时间复杂度都不固定：

因为咋们的gap是按照Knuth提出的方式取值的，而且Knuth进行了大量的试验统计，我们暂时就按照：O(n^{1.25})到O(1.6*n^{1.25})来算。

4. 稳定性：不稳定

2.2.3 代码实现

  1. //平均O(n^1.3)
  2. void ShellSort(int* a, int n)
  3. {
  4. 	int gap = n;
  5.  
  6. 	// gap > 1时是预排序，目的让他接近有序
  7. 	// gap == 1是直接插入排序，目的是让他有序
  8. 	while (gap > 1)
  9. 	{
  10. 		gap = gap / 3 + 1;
  11. 		for (int i = 0; i < n - gap; i++)
  12. 		{
  13. 			int end = i;
  14. 			int tmp = a[end + gap];
  15. 			while (end >= 0)
  16. 			{
  17. 				if (tmp < a[end])
  18. 				{
  19. 					a[end + gap] = a[end];
  20. 					end -= gap;
  21. 				}
  22. 				else
  23. 				{
  24. 					break;
  25. 				}
  26. 			}
  27. 			a[end + gap] = tmp;
  28. 		}
  29. 	}
  30.  
  31. 	//优化之前
  32. 	/*while (gap > 1)
  33. 	{
  34. 		gap = gap / 3 + 1;
  35. 		for (int j = 0; j < gap; ++j)
  36. 		{
  37. 			for (int i = j; i < n - gap; i += gap)
  38. 			{
  39. 				int end = i;
  40. 				int tmp = a[end + gap];
  41. 				while (end >= 0)
  42. 				{
  43. 					if (tmp < a[end])
  44. 					{
  45. 						a[end + gap] = a[end];
  46. 						end -= gap;
  47. 					}
  48. 					else
  49. 					{
  50. 						break;
  51. 					}
  52. 				}
  53. 				a[end + gap] = tmp;
  54. 			}
  55. 		}
  56. 	}*/
  57. }

三、选择排序

3.1 直接选择排序

3.1.1 基本思想

选择排序是一种简单直观的排序算法，它的基本思想是每次从待排序的数组中选择最小（或最大）的元素，放到已排序部分的末尾，直到整个数组有序为止。

具体的步骤如下：

  1. 遍历数组，从第一个元素开始，将其标记为最小元素。
  2. 在剩下的待排序部分中，找到最小的元素，并将其与待排序部分的第一个元素交换位置。
  3. 指针向后移动一位，进入下一轮遍历，重复步骤2，直到遍历完整个数组。

选择排序的时间复杂度为O(n^2)，其中n为数组的长度。无论原始数组是否有序，每次都需要遍历剩余的待排序部分来找到最小元素，因此时间复杂度较高。

选择排序是一种原地排序算法，它只需要常数级的额外空间来存储交换时的临时变量，因此空间复杂度为O(1)。

选择排序是一种不稳定的排序算法，因为交换元素的位置可能会改变相同元素的相对顺序。例如，对于序列[5, 5, 2]，第一轮选择排序后，第一个5会与2交换位置，导致相同元素的顺序改变。

尽管选择排序的性能不如快速排序、归并排序等高级排序算法，但它简单易懂，实现起来较为简单，适用于小规模的数据排序或作为其他高级排序算法的辅助排序步骤。

3.1.2 特性总结

  1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
  2. 时间复杂度：O(N^2)
  3. 空间复杂度：O(1)
  4. 稳定性：不稳定

3.1.3 代码实现

  1. void swap(int* p1, int* p2)
  2. {
  3. 	int tmp = *p1;
  4. 	*p1 = *p2;
  5. 	*p2 = tmp;
  6. }
  7.  
  8. //优化了一步，一次选两个，一个最大，一个最小
  9. void SelectSort(int* a, int n)
  10. {
  11. 	int begin = 0, end = n - 1;
  12. 	while(begin < end)
  13. 	{
  14. 		int mini = begin, maxi = begin;
  15. 		for (int i = begin + 1; i <= end; i++)
  16. 		{
  17. 			if (a[i] < a[mini])
  18. 			{
  19. 				mini = i;
  20. 			}
  21. 			if (a[i] > a[maxi])
  22. 			{
  23. 				maxi = i;
  24. 			}
  25. 		}
  26. 		swap(&a[begin], &a[mini]);
  27. 		if (maxi == begin)
  28. 		{
  29. 			maxi = mini;
  30. 		}
  31. 		swap(&a[end], &a[maxi]);
  32.  
  33. 		begin++;
  34. 		end--;
  35. 	}
  36. }

3.2 堆排序

3.2.1 基本思想

堆排序是一种基于完全二叉堆的排序算法。它的基本思想是通过将待排序的数组看作是一个完全二叉树，并将其转化为一个最大堆或最小堆。然后，每次将堆顶元素与堆的最后一个元素交换位置，然后调整堆，使得剩余元素满足堆的性质。重复这个过程，直到整个数组有序为止。

具体的步骤如下：

  1. 将待排序的数组构建成一个最大堆或最小堆。
  2. 交换堆顶元素与堆的最后一个元素，然后将剩余元素调整为一个新的堆。
  3. 重复步骤2，直到堆的大小为1，则整个数组有序。

堆排序的时间复杂度为O(nlogn)，其中n为数组的长度。构建堆的过程需要O(n)的时间复杂度，而每次调整堆的时间复杂度为O(logn)，总共需要进行n-1次交换和调整操作。

堆排序是一种原地排序算法，它只需要常数级别的额外空间来存储交换时的临时变量，因此空间复杂度为O(1)。

堆排序是一种不稳定的排序算法，因为交换堆顶元素与最后一个元素可能会改变相同元素的相对顺序。

虽然堆排序的时间复杂度较低，但它的常数项较大，而且在实际应用中不如快速排序或归并排序常用，一般用于特定场景或作为其他排序算法的辅助排序步骤。

3.2.2 特性总结

  1. 堆排序使用堆来选数，效率就高了很多。
  2. 时间复杂度：O(N*logN)
  3. 空间复杂度：O(1)
  4. 稳定性：不稳定

3.2.3 代码实现

  1. void Swap(int* p1, int* p2)
  2. {
  3. 	int t = *p1;
  4. 	*p1 = *p2;
  5. 	*p2 = t;
  6. }
  7.  
  8. void AdjustDown(int* a, int size, int parent) //这里的size表示最后要建成的最终形态的堆的大小
  9. {
  10. 	int child = parent * 2 + 1;
  11.  
  12. 	while (child < size)
  13. 	{
  14. 		if (child + 1 < size && a[child + 1] > a[child])
  15. 		{
  16. 			child++;
  17. 		}
  18.  
  19. 		if (a[child] > a[parent])
  20. 		{
  21. 			Swap(&a[child], &a[parent]);
  22. 			parent = child;
  23. 			child = child * 2 + 1;
  24. 		}
  25. 		else
  26. 		{
  27. 			break;
  28. 		}
  29. 	}
  30. }
  31.  
  32. void HeapSort(int* a, int n)
  33. {
  34. 	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
  35. 	{
  36. 		AdjustDown(a, n, i);
  37. 	}
  38.  
  39. 	for (int i = n - 1; i > 0; i--)
  40. 	{
  41. 		Swap(&a[0], &a[i]);
  42. 		AdjustDown(a, i, 0);
  43. 	}
  44. }

 

四、交换排序

4.1 冒泡排序

4.1.1 基本思想

冒泡排序是一种简单的排序算法，它重复地遍历待排序数组，每次比较相邻的两个元素，并将较大（或较小）的元素交换到右侧。通过多次遍历，最大（或最小）的元素会逐渐移动到右侧，实现排序的目的。

具体的步骤如下：

  1. 从数组的第一个元素开始，依次比较相邻的两个元素，如果前一个元素大于（或小于）后一个元素，则交换它们的位置。
  2. 继续遍历剩下的元素，进行相同的比较和交换操作，直到遍历完整个数组。
  3. 重复上述步骤，每次遍历都会将当前最大（或最小）的元素移动到右侧。
  4. 重复执行n-1次遍历，直到所有元素都有序排列。

冒泡排序的时间复杂度为O(n^2)，其中n为数组的长度。每次遍历需要比较n-1次，并且最多需要执行n-1次遍历。

冒泡排序是一种原地排序算法，它只需要常数级别的额外空间来存储交换时的临时变量，因此空间复杂度为O(1)。

冒泡排序是一种稳定的排序算法，因为在相邻元素比较时，只有前一个元素大于（或小于）后一个元素时才会交换它们的位置。

尽管冒泡排序的时间复杂度较高，但它的实现简单，适用于小规模的数据排序。在实际应用中，由于其性能较差，常常被其他高效的排序算法取代。


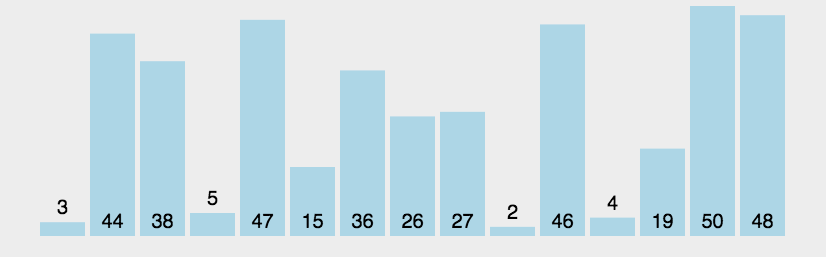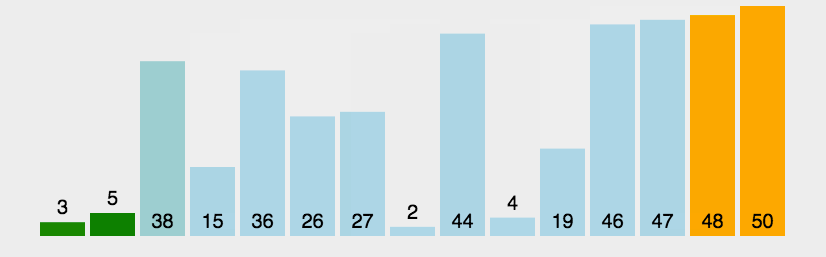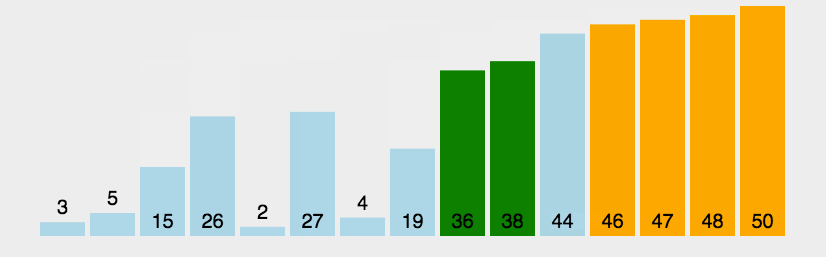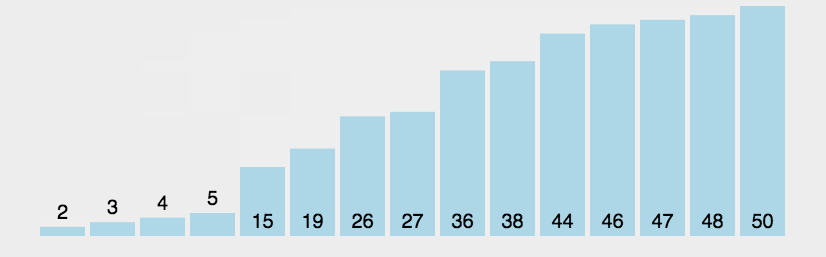
4.1.2 特性总结

  1. 冒泡排序是一种非常容易理解的排序
  2. 时间复杂度：O(N^2)
  3. 空间复杂度：O(1)
  4. 稳定性：稳定

4.1.3 代码实现

  1. void swap(int* p1, int* p2)
  2. {
  3. 	int tmp = *p1;
  4. 	*p1 = *p2;
  5. 	*p2 = tmp;
  6. }
  7.  
  8. void BubbleSort(int* a, int n)
  9. {
  10. 	for (int j = 0; j < n - 1; j++)
  11. 	{
  12. 		bool exchange = false;
  13. 		for (int i = 0; i < n - 1 - j; i++)
  14. 		{
  15. 			if (a[i] > a[i + 1])
  16. 			{
  17. 				swap(&a[i], &a[i + 1]);
  18. 				exchange = true;
  19. 			}
  20. 		}
  21.  
  22. 		if (exchange == false)
  23. 		{
  24. 			break;
  25. 		}
  26. 	}
  27. }

4.2 快速排序

4.2.1 基本思想

快速排序是一种常用的排序算法，它采用分治的思想将数据分成较小和较大的两部分，然后递归地对两部分进行排序。

具体的步骤如下（hoare版本）：

  1. 选择一个基准元素（pivot），通常选择数组的第一个或最后一个元素。
  2. 将数组分为两部分，使得左边部分的元素都小于等于基准元素，右边部分的元素都大于等于基准元素。可以使用两个指针分别从数组的左右两端开始遍历，当左指针指向的元素大于基准元素，右指针指向的元素小于基准元素时，交换它们的位置。
  3. 递归地对左右两部分进行排序，直到每个部分只有一个元素或为空。
  4. 合并排序后的左右部分，即可得到完整的有序数组。

快速排序的时间复杂度平均为O(nlogn)，其中n为数组的长度。每次排序都会将数组分成大致等长的两部分，因此分治的次数为logn，而每次分治需要遍历n个元素，所以时间复杂度为nlogn。最坏情况下的时间复杂度为O(n^2)，当数组已经有序或近乎有序时，每次分治只能得到一个元素，导致分治次数为n，时间复杂度变为n的平方。

快速排序是一种原地排序算法，它只需要常数级别的额外空间来存储分治时的临时变量，因此空间复杂度为O(1)。

快速排序是一种不稳定的排序算法，因为在交换元素时可能改变相同元素的相对顺序。

快速排序是一种高效的排序算法，常被用于大规模数据的排序。它的实现相对较复杂，但其时间复杂度的平均性能优势使其成为了主流的排序算法之一。

前后指针版本

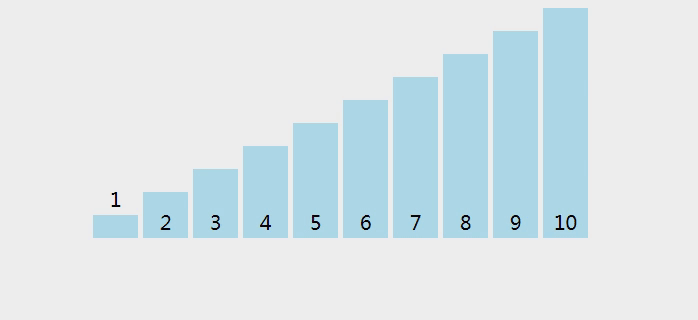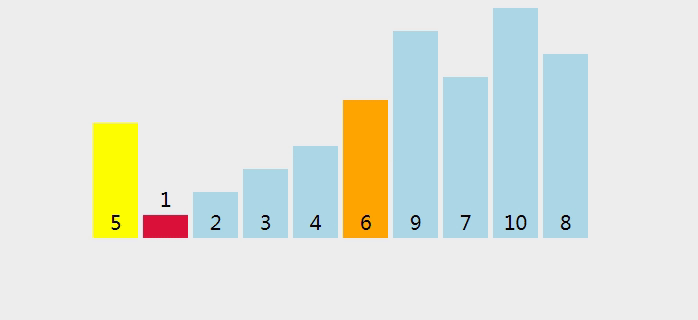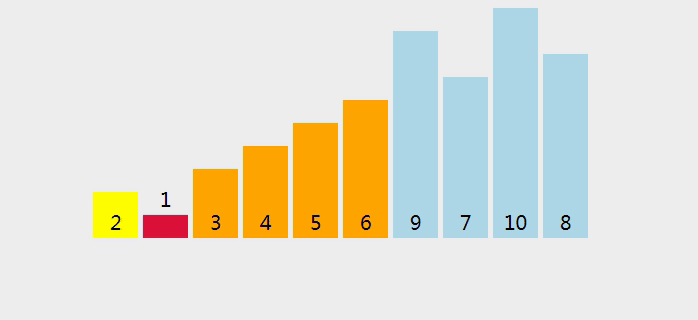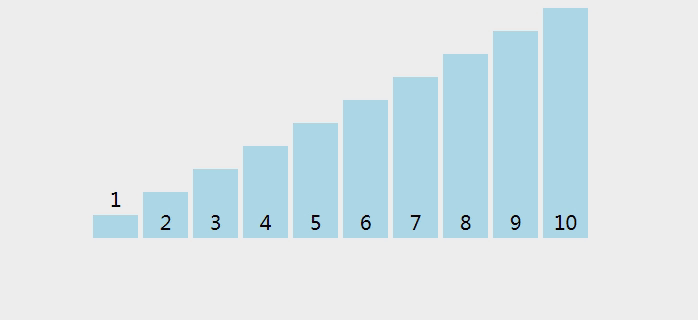
4.2.2 特性总结

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(logN)

4. 稳定性：不稳定

4.2.3 代码实现

  1. void Swap(int* p1, int* p2)
  2. {
  3. 	int t = *p1;
  4. 	*p1 = *p2;
  5. 	*p2 = t;
  6. }
  7.  
  8. int GetMidi(int* a, int begin, int end)
  9. {
  10. 	int midi = (begin + end) / 2;
  11. 	//begin midi end 三个数取中
  12. 	if (a[begin] < a[midi])
  13. 	{
  14. 		if (a[midi] < a[end])
  15. 			return midi;
  16. 		else if (a[begin] > a[end])
  17. 			return begin;
  18. 		else
  19. 			return end;
  20. 	}
  21. 	else // a[begin] > a[midi]
  22. 	{
  23. 		if (a[midi] > a[end])
  24. 			return midi;
  25. 		else if (a[begin] < a[end])
  26. 			return begin;
  27. 		else
  28. 			return end;
  29. 	}
  30. }
  31.  
  32. //hoare版本
  33. int PartSort1(int* a, int begin, int end)
  34. {
  35. 	int midi = GetMidi(a, begin, end);
  36. 	Swap(&a[midi], &a[begin]);
  37.  
  38. 	int left = begin, right = end;
  39. 	int keyi = left;
  40.  
  41. 	while (left < right)
  42. 	{
  43. 		while (left < right && a[right] >= a[keyi])
  44. 		{
  45. 			right--;
  46. 		}
  47. 		while (left < right && a[left] <= a[keyi])
  48. 		{
  49. 			left++;
  50. 		}
  51. 		Swap(&a[left], &a[right]);
  52. 	}
  53.  
  54. 	Swap(&a[keyi], &a[left]);
  55.  
  56. 	return left;
  57. }
  58.  
  59. //挖坑法版本
  60. int PartSort2(int* a, int begin, int end)
  61. {
  62. 	int midi = GetMidi(a, begin, end);
  63. 	Swap(&a[midi], &a[begin]);
  64.  
  65. 	int key = a[begin];
  66. 	int hole = begin;
  67. 	while (begin < end)
  68. 	{
  69. 		// 右边找小，填到左边的坑
  70. 		while (begin < end && a[end] >= key)
  71. 		{
  72. 			--end;
  73. 		}
  74.  
  75. 		a[hole] = a[end];
  76. 		hole = end;
  77.  
  78. 		// 左边找大，填到右边的坑
  79. 		while (begin < end && a[begin] <= key)
  80. 		{
  81. 			++begin;
  82. 		}
  83.  
  84. 		a[hole] = a[begin];
  85. 		hole = begin;
  86. 	}
  87.  
  88. 	a[hole] = key;
  89. 	return hole;
  90. }
  91.  
  92. //前后指针版本
  93. int PartSort3(int* a, int begin, int end)
  94. {
  95. 	int midi = GetMidi(a, begin, end);
  96. 	Swap(&a[midi], &a[begin]);
  97. 	int keyi = begin;
  98.  
  99. 	int prev = begin;
  100. 	int cur = prev + 1;
  101. 	while (cur <= end)
  102. 	{
  103. 		if (a[cur] < a[keyi] && ++prev != cur)
  104. 			Swap(&a[prev], &a[cur]);
  105.  
  106. 		++cur;
  107. 	}
  108.  
  109. 	Swap(&a[prev], &a[keyi]);
  110.  
  111. 	return prev;
  112. }
  113.  
  114. void QuickSort(int* a, int begin, int end)
  115. {
  116. 	if (begin >= end)
  117. 		return;
  118.  
  119. 	int keyi = PartSort3(a, begin, end);
  120. 	QuickSort(a, begin, keyi - 1);
  121. 	QuickSort(a, keyi + 1, end);
  122. }

 

五、归并排序

5.1 归并排序

5.1.1 基本思想

归并排序是一种分治算法，它将待排序数组分成两个部分，分别对每个部分进行排序，然后将两个排好序的部分合并成一个有序的数组。

具体的步骤如下：

  1. 将数组不断二分，直到每个部分只有一个元素或为空。
  2. 递归地对左右两部分进行排序，直到每个部分只有一个元素或为空。
  3. 合并排序后的左右两部分，即可得到完整的有序数组。合并时，从两个部分的头部开始比较元素大小，较小的元素先放入新数组，然后将指针向后移动，直到一个部分为空，再将另一个部分的剩余元素依次放入新数组。

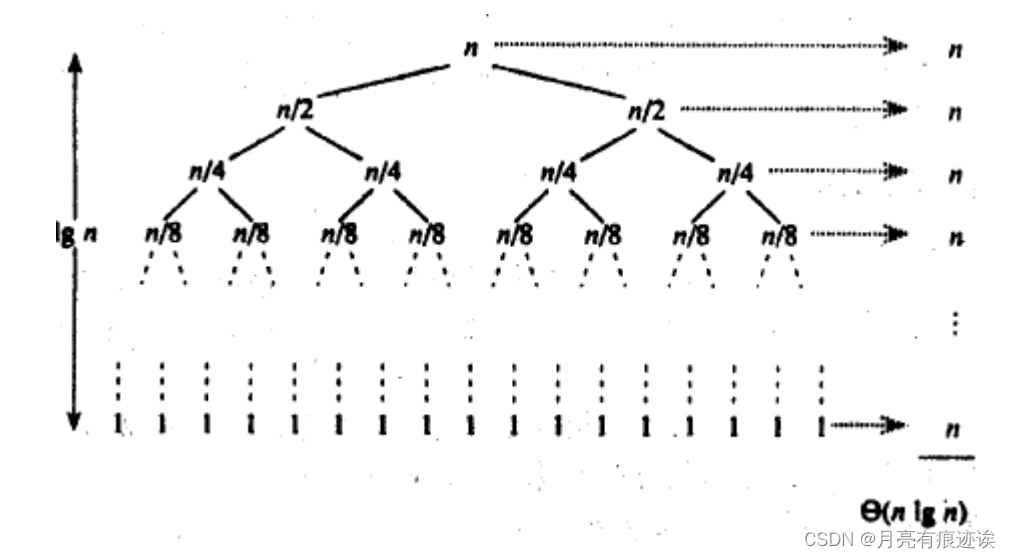
归并排序的时间复杂度是O(nlogn)，其中n为数组的长度。每次排序时，需要将数组分成大致等长的两部分，因此分治的次数为logn。每次分治中合并两个部分的时间复杂度为O(n)，因为需要遍历n个元素。所以总的时间复杂度为nlogn。

归并排序是一种稳定的排序算法，因为在合并两部分时，如果遇到相同元素，会先将左半部分的元素放入新数组，保证了相同元素的相对顺序不会改变。

归并排序是一种稳定、可靠的排序算法，它的实现相对简单，但其时间复杂度的稳定性使其成为了主流的排序算法之一。它也适用于大规模数据的排序，特别适合用于链表等数据结构的排序。

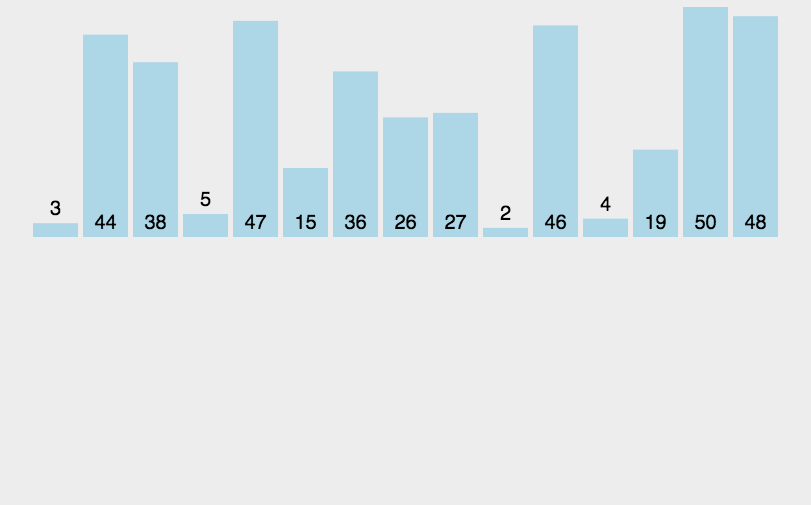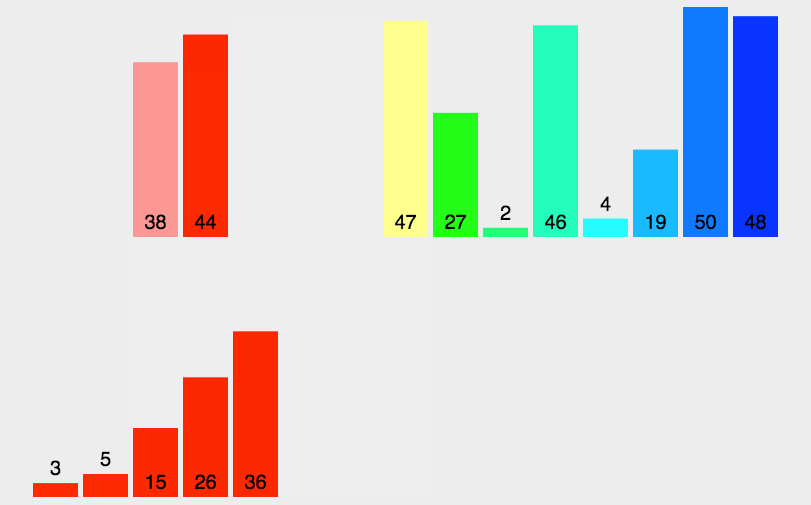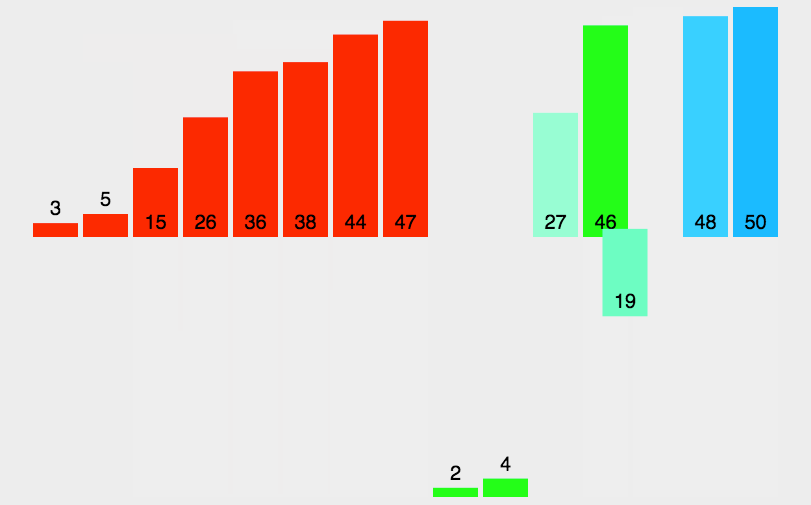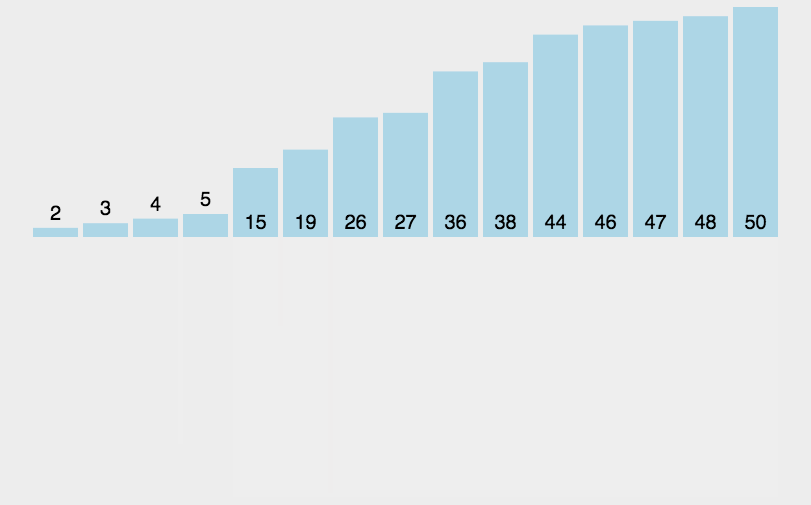
5.1.2 特征总结

  1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
  2. 时间复杂度：O(N*logN)
  3. 空间复杂度：O(N)
  4. 稳定性：稳定  

5.1.3 代码实现

  1. void Swap(int* p1, int* p2)
  2. {
  3. 	int t = *p1;
  4. 	*p1 = *p2;
  5. 	*p2 = t;
  6. }
  7.  
  8. void _MergeSort(int* a, int begin, int end, int* tmp)
  9. {
  10. 	if (begin >= end)
  11. 	{
  12. 		return;
  13. 	}
  14.  
  15. 	int mid = (begin + end) / 2;
  16.  
  17. 	_MergeSort(a, begin, mid, tmp);
  18. 	_MergeSort(a, mid + 1, end, tmp);
  19.  
  20. 	int begin1 = begin, end1 = mid;
  21. 	int begin2 = mid + 1, end2 = end;
  22. 	int i = begin;
  23. 	while (begin1 <= end1 && begin2 <= end2)
  24. 	{
  25. 		if (a[begin1] < a[begin2])
  26. 		{
  27. 			tmp[i++] = a[begin1++];
  28. 		}
  29. 		else
  30. 		{
  31. 			tmp[i++] = a[begin2++];
  32. 		}
  33. 	}
  34.  
  35. 	while (begin1 <= end1)
  36. 	{
  37. 		tmp[i++] = a[begin1++];
  38. 	}
  39.  
  40. 	while (begin2 <= end2)
  41. 	{
  42. 		tmp[i++] = a[begin2++];
  43. 	}
  44.  
  45. 	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
  46. }
  47.  
  48. void MergeSort(int* a, int n)
  49. {
  50. 	int* tmp = (int*)malloc(sizeof(int) * n);
  51. 	if (tmp == NULL)
  52. 	{
  53. 		perror("malloc fail");
  54. 		return;
  55. 	}
  56.  
  57. 	_MergeSort(a, 0, n - 1, tmp);
  58.  
  59. 	free(tmp);
  60. }

 

六、计数排序

6.1 计数排序

6.1.1  基本思想

前面介绍的几种的排序都是比较排序算法，而计数排序是一种非比较排序算法，其基本思想是统计待排序数组中每个元素出现的次数，然后按照元素的大小顺序依次将元素放入新的数组中。

具体的步骤如下：

  1. 找出待排序数组中最大值max和最小值min。
  2. 创建一个大小为max-min+1的计数数组count，用于记录每个元素出现的次数。初始时，count数组的所有元素都为0。
  3. 遍历待排序数组，将每个元素的值作为count数组的索引，在对应的索引位置上将计数加1。
  4. 依次累加count数组中的元素，即将count中的元素与前一个元素相加，得到每个元素在排序后数组中的最后一个位置的索引。
  5. 创建一个大小与待排序数组相同的临时数组temp。
  6. 遍历待排序数组，根据元素的值在count数组中查找对应的位置，并将元素放入temp数组中。然后将count数组中对应位置的计数值减1。
  7. 将temp数组的元素复制回原始数组，即得到了排序后的数组。

计数排序的时间复杂度是O(n+k)，其中n为数组的长度，k为待排序数组中最大值与最小值之差。由于需要遍历待排序数组两次，分别用于计数和复制元素，因此实际的时间复杂度可以近似为O(n)。

计数排序是一种稳定的排序算法，因为在将元素放入临时数组时，遇到相同值的元素会按照待排序数组中的顺序依次放入，保持了相同元素的相对顺序不变。计数排序适用于待排序数组中的元素范围相对较小的情况，对于较大范围的数据集合，计数排序的空间复杂度较高，不适合使用。

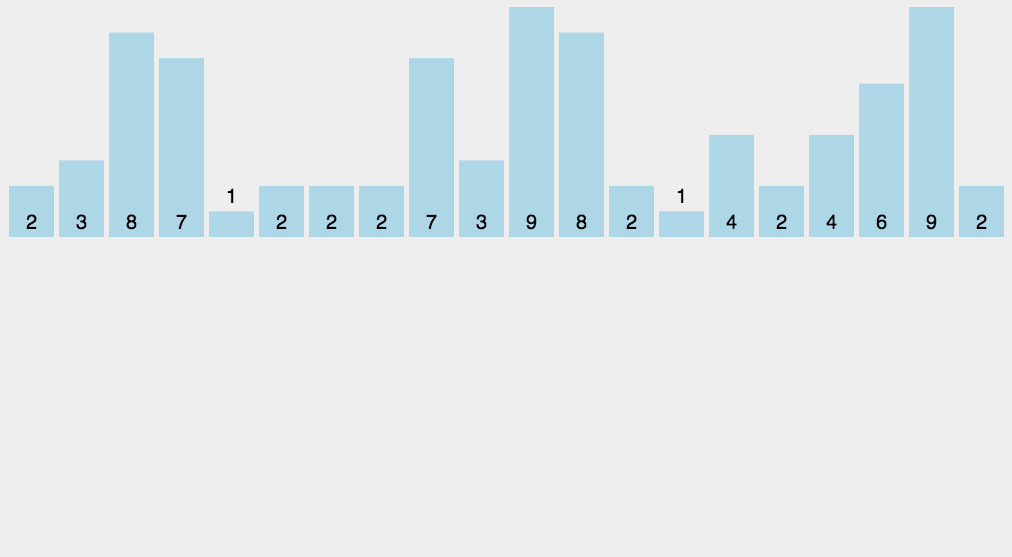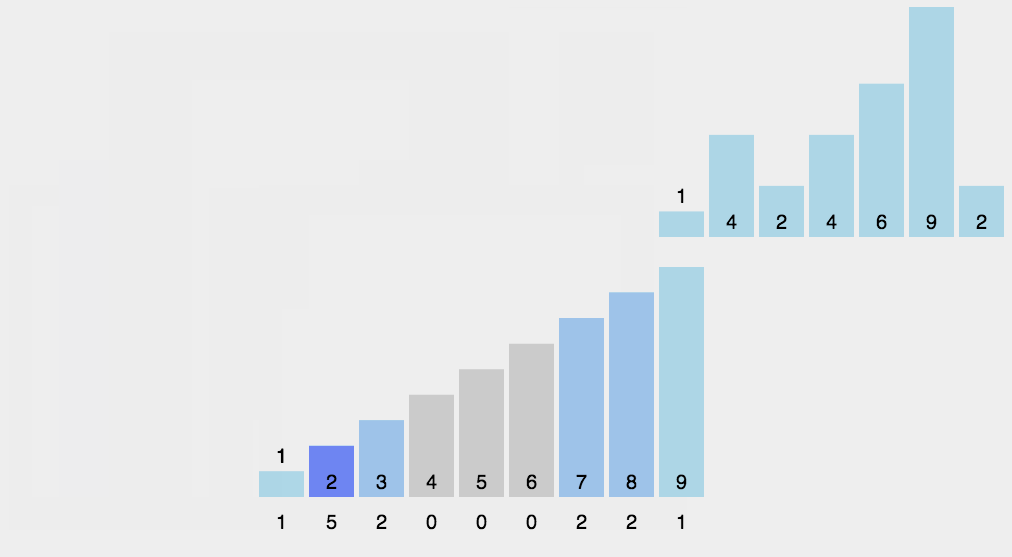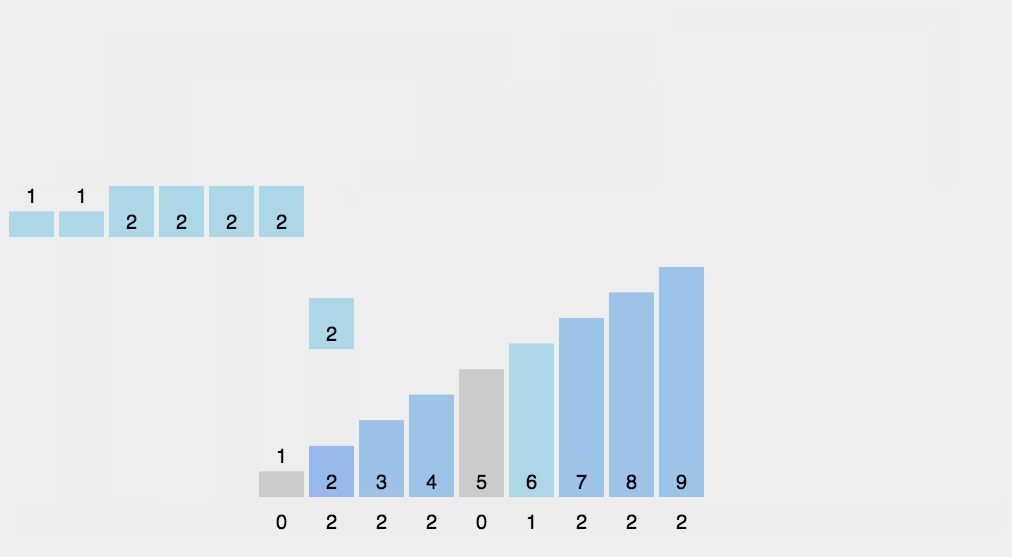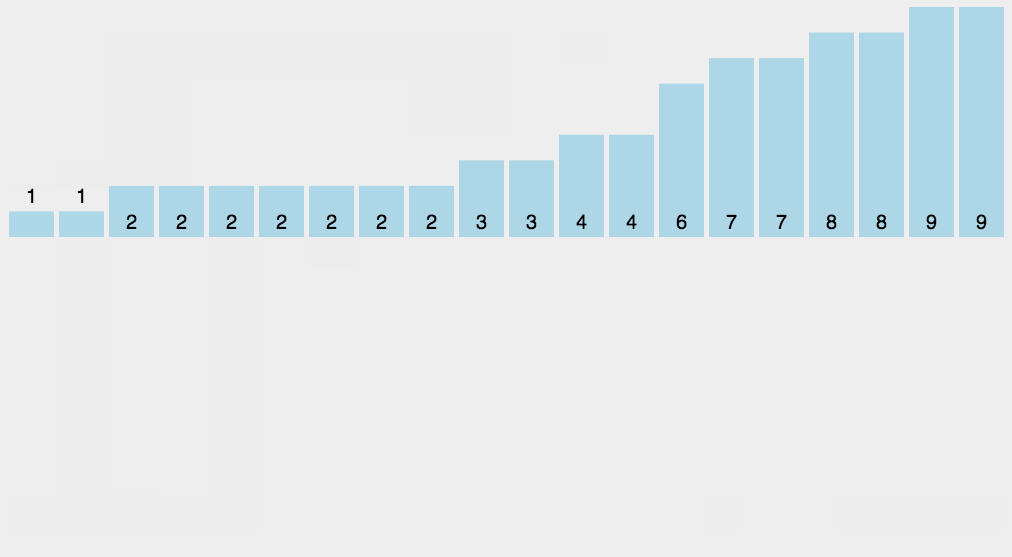
6.1.2 特征总结

  1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
  2. 时间复杂度：O(MAX(N,范围))
  3. 空间复杂度：O(范围)
  4. 稳定性：稳定（可以做到稳定，但一般不谈稳定性）

6.1.3 代码实现

  1. void CountSort(int* a, int n)
  2. {
  3. 	int min = a[0], max = a[0];
  4. 	for (int i = 1; i < n; i++)
  5. 	{
  6. 		if (a[i] < min)
  7. 		{
  8. 			min = a[i];
  9. 		}
  10. 		if (a[i] > max)
  11. 		{
  12. 			max = a[i];
  13. 		}
  14. 	}
  15.  
  16. 	int range = max - min + 1;
  17. 	int* count = (int*)calloc(range, sizeof(int));
  18. 	if (count == NULL)
  19. 	{
  20. 		perror("calloc fail\n");
  21. 		return;
  22. 	}
  23.  
  24. 	for (int i = 0; i < n; i++)
  25. 	{
  26. 		count[a[i] - min]++;
  27. 	}
  28.  
  29. 	int j = 0;
  30. 	for (int i = 0; i < range; i++)
  31. 	{
  32. 		while (count[i]--)
  33. 		{
  34. 			a[j++] = i + min;
  35. 		}
  36. 	}
  37. }

 

七、排序比较

 

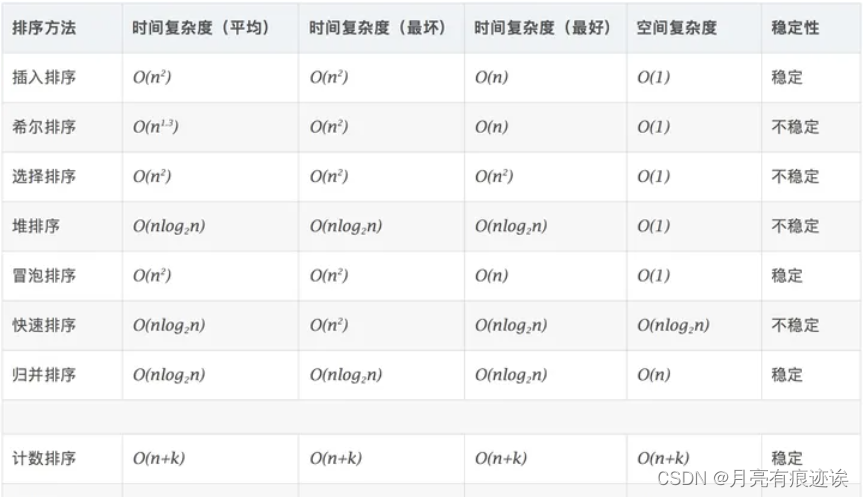
总结

通过对各种排序算法的学习，希望读者能够了解排序算法的基本原理和特点，以便根据实际需求选择合适的算法。希望本文能为你在排序算法的学习和实践中提供有益的帮助，让你在未来的工作和学习中能够游刃有余地运用排序算法，提升数据处理效率，创造更多价值。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/163773
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号