devbox
繁依Fanyi0
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

PPO算法（附pytorch代码）

作者：繁依Fanyi0 | 2024-03-01 05:52:46

赞

踩

ppo算法

这里写目录标题

一、PPO算法

（1）简介

  • PPO算法是一种强化学习中的策略梯度方法，它的全称是Proximal Policy Optimization，即近端策略优化1。PPO算法的目标是在与环境交互采样数据后，使用随机梯度上升优化一个“替代”目标函数，从而改进策略。PPO算法的特点是可以进行多次的小批量更新，而不是像标准的策略梯度方法那样每个数据样本只进行一次梯度更新12。
  • PPO算法有两种主要的变体：PPO-Penalty和PPO-Clip。PPO-Penalty类似于TRPO算法，它使用KL散度作为一个约束条件，但是将KL散度作为目标函数的一个惩罚项，而不是一个硬性约束，并且自动调整惩罚系数，使其适应数据的规模12。PPO-Clip则没有KL散度项，也没有约束条件，而是使用一种特殊的裁剪技术，在目标函数中消除了新策略远离旧策略的动机。
  • PPO同样使用了AC框架，不过相比DPG更加接近传统的PG算法，采用的是随机分布式的策略函数（Stochastic Policy），智能体（agent）每次决策时都要从策略函数输出的分布中采样，得到的样本作为最终执行的动作，因此天生具备探索环境的能力，不需要为了探索环境给决策加上扰动；PPO的重心会放到actor上，仅仅将critic当做一个预测状态好坏（在该状态获得的期望收益）的工具，策略的调整基准在于获取的收益，不是critic的导数。

（2）On-policy？

  • PPO 算法是一个 on-policy 的算法。123

  • PPO算法是一种基于策略的强化学习算法，它可以处理连续动作空间的问题。PPO算法是一种在线算法，也就是说它需要用当前的策略产生数据，并用这些数据更新策略。PPO算法不能直接使用经验回放，因为经验回放中的数据可能是由不同的策略产生的，这会导致策略梯度的偏差12。

    但是，PPO算法可以使用一种技术叫做重要性采样（importance sampling），来利用之前的数据进行多步更新23。重要性采样的思想是给每个数据加上一个权重，表示目标策略和行为策略的比例24。这样，PPO算法可以在一定程度上提高数据的利用效率，而不影响策略梯度的正确性23。

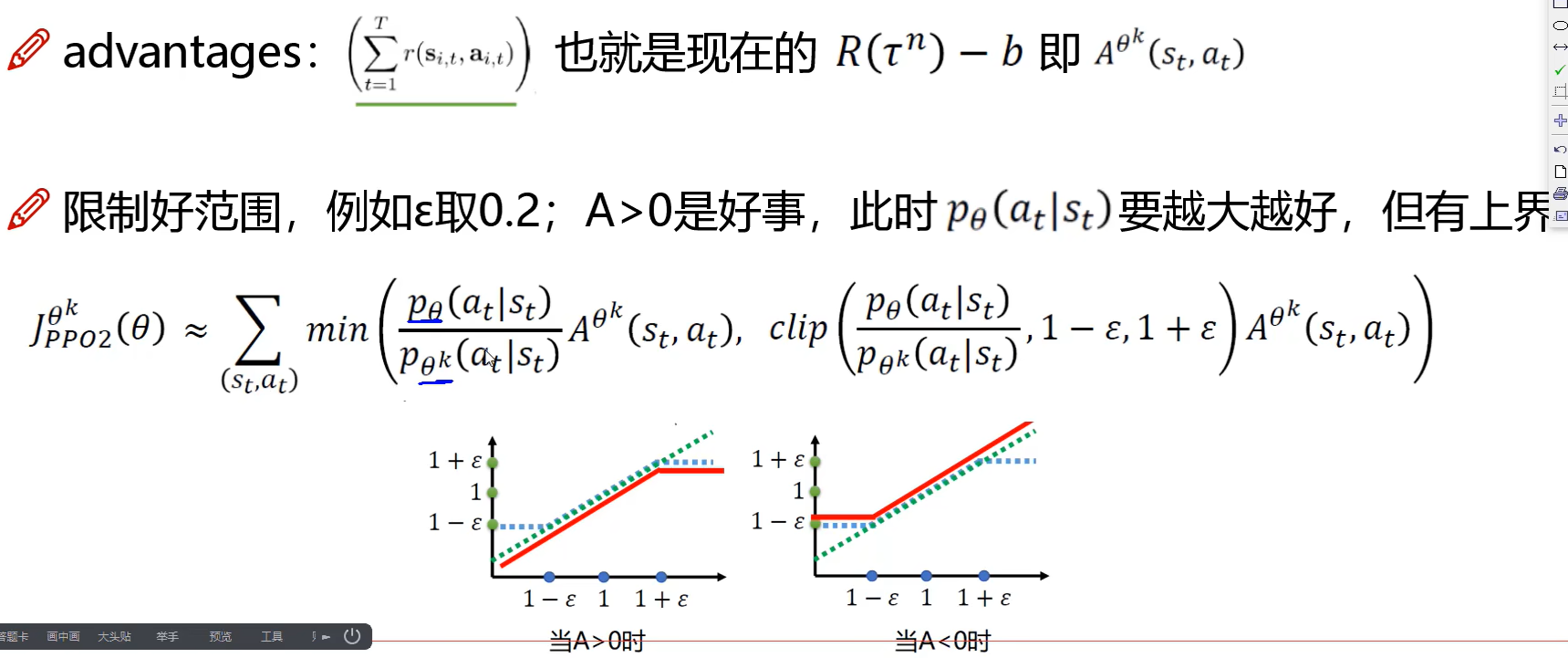
  • PPO 算法的原理是在每一步更新策略时，尽量减小代价函数，同时保证新策略和旧策略的差异不要太大。为了做到这一点，PPO 算法使用了一个特殊的目标函数，它包含了一个截断的比率因子，用来限制新策略和旧策略的比例。1
    在这里插入图片描述
    在这里插入图片描述
    参考链接点击

  • 重要性采样是一种调整数据权重的方法，它可以用于在线算法，也可以用于离线算法。PPO算法使用了重要性采样，但它并没有使用经验回放中的随机抽样和淘汰机制，而是按照时间顺序使用数据，并在一定次数后丢弃数据 。
    在这里插入图片描述

  • PPO 算法只使用当前策略产生的经验来更新网络，而不使用历史策略产生的经验。这意味着 PPO 算法需要在每次更新策略后丢弃之前收集的经验，因为它们不再适用于新的策略。这样做的好处是 PPO 算法可以保证策略和值函数之间的一致性，也就是说，值函数可以很好地估计当前策略的性能。2

  • 虽然 PPO 算法可以使用经验回放缓冲区来存储和重用历史经验，但这并不改变它是一个 on-policy 的算法。因为 PPO 算法在使用缓冲区中的数据时，仍然需要计算新策略和旧策略的比例，并且使用截断的比率因子来限制更新幅度。这样做相当于对 off-policy 的数据进行了校正，使得它们更接近 on-policy 的数据。4

  • 如果 PPO 算法使用经验回放，那么它需要对 off-policy 的数据进行一些校正，以减小偏差和方差。一种常用的校正方法是使用重要性采样权重 (ISW)，它可以衡量数据的分布和当前策略的分布之间的差异，并对损失函数或者优势函数进行加权。12

  • 另一种校正方法是使用优先级经验回放 (PER)，它可以根据数据的价值或者优势来给数据分配优先级，并按照优先级来采样数据。这样可以使得更有价值或者更有优势的数据被更频繁地采样，从而提高学习效率。2

（3）GAE （Generalized Advantage Estimation)

  • 它是一种用于估计优势函数的方法。12
  • 优势函数是指在某个状态下，采取某个动作比按照当前策略采取动作所能获得的期望回报的差值。优势函数可以用来减少策略梯度估计的方差，提高学习效率。
  • GAE 的思想是利用值函数来对优势函数进行多步估计，同时使用一个衰减因子来平滑不同步长的估计，从而得到一个既有较小偏差又有较小方差的优势函数估计。具体来说，GAE 使用以下公式来计算优势函数估计：
    在这里插入图片描述
    具体实现：
# 定义折扣因子和平滑因子
gamma = 0.99
lambda = 0.95

# 初始化优势函数估计和回报估计为空列表
advantages = []
returns = []

# 初始化时间差分误差为0
delta = 0

# 从最后一个时间步开始反向遍历经验
for state, action, reward, next_state, done in reversed(experiences):

    # 如果是终止状态，那么下一个状态的值为0，否则用值函数网络预测
    if done:
        next_value = 0
    else:
        next_value = value_network.predict(next_state)

    # 计算当前状态的值
    value = value_network.predict(state)

    # 计算时间差分误差
    delta = reward + gamma * next_value - value

    # 计算优势函数估计，使用时间差分误差和上一个时间步的优势函数估计
    advantage = delta + gamma * lambda * advantage

    # 计算回报估计，使用奖励和下一个状态的值
    return = reward + gamma * next_value

    # 将优势函数估计和回报估计插入到列表的开头
    advantages.insert(0, advantage)
    returns.insert(0, return)

# 将优势函数估计和回报估计转换为张量
advantages = torch.tensor(advantages)
returns = torch.tensor(returns)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39

注意一下几点：

  1. 为什么要从最后一个时间步开始反向遍历
    答：为了利用之前计算的优势函数估计和回报估计来加速计算。如果从第一个时间步开始正向遍历，那么每个时间步都需要计算一个无限级数的和，这样会很慢。而如果从最后一个时间步开始反向遍历，那么每个时间步只需要用一个时间差分误差和上一个时间步的优势函数估计来计算当前的优势函数估计，这样会很快。同理，回报估计也可以用奖励和下一个状态的值来递推计算，而不需要用一个无限级数的和。
  2. 代码中returns有什么作用？
    答：returns 是用来存储每个时间步的回报估计的，回报估计是指从当前状态开始，按照当前策略采取动作所能获得的未来折扣奖励之和的期望。回报估计可以用来更新值函数网络，使其更接近真实的状态值。回报估计也可以用来计算优势函数，如果没有值函数网络的话。

三、代码

'''
@Author  ：Yan JP
@Created on Date：2023/4/19 17:31 
'''
# https://blog.csdn.net/dgvv4/article/details/129496576?spm=1001.2101.3001.6650.3&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EYuanLiJiHua%7EPosition-3-129496576-blog-117329002.235%5Ev29%5Epc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EYuanLiJiHua%7EPosition-3-129496576-blog-117329002.235%5Ev29%5Epc_relevant_default_base3&utm_relevant_index=6
# 代码用于离散环境的模型
import numpy as np
import torch
from torch import nn
from torch.nn import functional as F


# ----------------------------------- #
# 构建策略网络--actor
# ----------------------------------- #

class PolicyNet(nn.Module):
    def __init__(self, n_states, n_hiddens, n_actions):
        super(PolicyNet, self).__init__()
        self.fc1 = nn.Linear(n_states, n_hiddens)
        self.fc2 = nn.Linear(n_hiddens, n_actions)

    def forward(self, x):
        x = self.fc1(x)  # [b,n_states]-->[b,n_hiddens]
        x = F.relu(x)
        x = self.fc2(x)  # [b, n_actions]
        x = F.softmax(x, dim=1)  # [b, n_actions]  计算每个动作的概率
        return x


# ----------------------------------- #
# 构建价值网络--critic
# ----------------------------------- #

class ValueNet(nn.Module):
    def __init__(self, n_states, n_hiddens):
        super(ValueNet, self).__init__()
        self.fc1 = nn.Linear(n_states, n_hiddens)
        self.fc2 = nn.Linear(n_hiddens, 1)

    def forward(self, x):
        x = self.fc1(x)  # [b,n_states]-->[b,n_hiddens]
        x = F.relu(x)
        x = self.fc2(x)  # [b,n_hiddens]-->[b,1]  评价当前的状态价值state_value
        return x


# ----------------------------------- #
# 构建模型
# ----------------------------------- #

class PPO:
    def __init__(self, n_states, n_hiddens, n_actions,
                 actor_lr, critic_lr, lmbda, epochs, eps, gamma, device):
        # 实例化策略网络
        self.actor = PolicyNet(n_states, n_hiddens, n_actions).to(device)
        # 实例化价值网络
        self.critic = ValueNet(n_states, n_hiddens).to(device)
        # 策略网络的优化器
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        # 价值网络的优化器
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)

        self.gamma = gamma  # 折扣因子
        self.lmbda = lmbda  # GAE优势函数的缩放系数
        self.epochs = epochs  # 一条序列的数据用来训练轮数
        self.eps = eps  # PPO中截断范围的参数
        self.device = device

    # 动作选择
    def take_action(self, state):
        # 维度变换 [n_state]-->tensor[1,n_states]
        state = torch.tensor(state[np.newaxis, :]).to(self.device)
        # 当前状态下，每个动作的概率分布 [1,n_states]
        probs = self.actor(state)
        # 创建以probs为标准的概率分布
        action_list = torch.distributions.Categorical(probs)
        # 依据其概率随机挑选一个动作
        action = action_list.sample().item()
        return action

    # 训练
    def learn(self, transition_dict):
        # 提取数据集
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).to(self.device).view(-1, 1)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).to(self.device).view(-1, 1)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).to(self.device).view(-1, 1)

        # 目标，下一个状态的state_value  [b,1]
        next_q_target = self.critic(next_states)
        # 目标，当前状态的state_value  [b,1]
        td_target = rewards + self.gamma * next_q_target * (1 - dones)
        # 预测，当前状态的state_value  [b,1]
        td_value = self.critic(states)
        # 目标值和预测值state_value之差  [b,1]
        td_delta = td_target - td_value

        # 时序差分值 tensor-->numpy  [b,1]
        td_delta = td_delta.cpu().detach().numpy()
        advantage = 0  # 优势函数初始化
        advantage_list = []

        # 计算优势函数
        for delta in td_delta[::-1]:  # 逆序时序差分值 axis=1轴上倒着取 [], [], []
            # 优势函数GAE的公式 :计算优势函数估计，使用时间差分误差和上一个时间步的优势函数估计
            advantage = self.gamma * self.lmbda * advantage + delta
            advantage_list.append(advantage)
        # 正序
        advantage_list.reverse()
        # numpy --> tensor [b,1]
        advantage = torch.tensor(advantage_list, dtype=torch.float).to(self.device)

        # 策略网络给出每个动作的概率，根据action得到当前时刻下该动作的概率
        old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach()

        # 一组数据训练 epochs 轮
        for _ in range(self.epochs):
            # 每一轮更新一次策略网络预测的状态
            log_probs = torch.log(self.actor(states).gather(1, actions))
            # 新旧策略之间的比例
            ratio = torch.exp(log_probs - old_log_probs)
            # 近端策略优化裁剪目标函数公式的左侧项
            surr1 = ratio * advantage
            # 公式的右侧项，ratio小于1-eps就输出1-eps，大于1+eps就输出1+eps
            surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage

            # 策略网络的损失函数
            actor_loss = torch.mean(-torch.min(surr1, surr2))
            # 价值网络的损失函数，当前时刻的state_value - 下一时刻的state_value
            critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))

            # 梯度清0
            self.actor_optimizer.zero_grad()
            self.critic_optimizer.zero_grad()
            # 反向传播
            actor_loss.backward()
            critic_loss.backward()
            # 梯度更新
            self.actor_optimizer.step()
            self.critic_optimizer.step()

import matplotlib.pyplot as plt
import gym
import torch
if __name__ == '__main__':


    device = torch.device('cuda') if torch.cuda.is_available() \
        else torch.device('cpu')

    # ----------------------------------------- #
    # 参数设置
    # ----------------------------------------- #

    num_episodes = 300  # 总迭代次数
    gamma = 0.9  # 折扣因子
    actor_lr = 1e-3  # 策略网络的学习率
    critic_lr = 1e-2  # 价值网络的学习率
    n_hiddens = 16  # 隐含层神经元个数
    env_name = 'CartPole-v0'
    return_list = []  # 保存每个回合的return

    # ----------------------------------------- #
    # 环境加载
    # ----------------------------------------- #

    env = gym.make(env_name)
    n_states = env.observation_space.shape[0]  # 状态数 4
    n_actions = env.action_space.n  # 动作数 2

    # ----------------------------------------- #
    # 模型构建
    # ----------------------------------------- #

    agent = PPO(n_states=n_states,  # 状态数
                n_hiddens=n_hiddens,  # 隐含层数
                n_actions=n_actions,  # 动作数
                actor_lr=actor_lr,  # 策略网络学习率
                critic_lr=critic_lr,  # 价值网络学习率
                lmbda=0.95,  # 优势函数的缩放因子
                epochs=10,  # 一组序列训练的轮次
                eps=0.2,  # PPO中截断范围的参数
                gamma=gamma,  # 折扣因子
                device=device
                )

    # ----------------------------------------- #
    # 训练--回合更新 on_policy
    # ----------------------------------------- #

    for i in range(num_episodes):

        state = env.reset()  # 环境重置
        done = False  # 任务完成的标记
        episode_return = 0  # 累计每回合的reward

        # 构造数据集，保存每个回合的状态数据
        transition_dict = {
            'states': [],
            'actions': [],
            'next_states': [],
            'rewards': [],
            'dones': [],
        }

        while not done:
            action = agent.take_action(state)  # 动作选择
            next_state, reward, done, _ = env.step(action)  # 环境更新
            # 保存每个时刻的状态\动作\...
            transition_dict['states'].append(state)
            transition_dict['actions'].append(action)
            transition_dict['next_states'].append(next_state)
            transition_dict['rewards'].append(reward)
            transition_dict['dones'].append(done)
            # 更新状态
            state = next_state
            # 累计回合奖励
            episode_return += reward

        # 保存每个回合的return
        return_list.append(episode_return)
        # 模型训练
        agent.learn(transition_dict)

        # 打印回合信息
        print(f'iter:{i}, return:{np.mean(return_list[-10:])}')

    # -------------------------------------- #
    # 绘图
    # -------------------------------------- #

    plt.plot(return_list)
    plt.title('return')
    plt.show()

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206
  • 207
  • 208
  • 209
  • 210
  • 211
  • 212
  • 213
  • 214
  • 215
  • 216
  • 217
  • 218
  • 219
  • 220
  • 221
  • 222
  • 223
  • 224
  • 225
  • 226
  • 227
  • 228
  • 229
  • 230
  • 231
  • 232
  • 233
  • 234
  • 235
  • 236

代码解析：

  1. log_probs = torch.log(self.actor(states).gather(1, actions))
  • self.actor(states) 是一个策略网络，它接受一批状态作为输入，输出每个状态下每个动作的概率分布，假设有 N 个状态，M 个动作，那么输出的形状是 (N, M)。
  • .gather(1, actions) 是一个张量操作，它根据 actions 中的索引从第一个维度上选取元素，actions 是一个形状为 (N, 1) 的张量，表示每个状态下实际采取的动作的索引，那么输出的形状也是 (N, 1)，表示每个状态下实际采取的动作的概率。
  • torch.log() 是一个张量操作，它对输入的每个元素取对数，输出的形状和输入相同，表示每个状态下实际采取的动作的对数概率。
    因此，这行代码最终得到一个形状为 (N, 1) 的张量，表示每个时间步的动作的对数概率。
  1. critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
    注意这里需要detach一下！！！！！！！！！
  2. PPO有价值网络critic，可以用目标网络吗？

  • PPO 有一个价值网络，用来估计状态值，并用于计算优势函数或者回报估计。理论上，PPO 也可以使用目标网络来生成目标状态值，从而稳定价值网络的训练。但是，PPO 是一个 on-policy 的算法，它只使用当前策略产生的经验来更新网络，而不使用历史策略产生的经验。这意味着 PPO 需要在每次更新策略后丢弃之前收集的经验，因为它们不再适用于新的策略。这样做的好处是 PPO 可以保证策略和值函数之间的一致性，也就是说，值函数可以很好地估计当前策略的性能。

  • 如果 PPO 使用目标网络，那么目标网络的参数会滞后于价值网络的参数，这可能导致目标状态值和价值网络输出之间的不一致性，也就是说，目标状态值可能不能很好地估计当前策略的性能。这样做的代价是 PPO 可能降低学习效率，因为它不能及时反映环境和策略的变化。

  • 因此，PPO 通常不使用目标网络，而是直接使用价值网络来生成目标状态值。这样做的好处是 PPO 可以提高学习效率，因为它可以及时反映环境和策略的变化。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/171436
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号