统计学学习日记：L8-参数估计_参数估计值

目录

一、估计量与估计值

二、评估统计量的标准

三、点估计 

四、区间估计

---

一、估计量与估计值

1.估计量：用于估计总体参数的随机变量

        如样本均值、样本比例、样本方差等

        例如：样本均值就是总体均值μ的一个估计量

2.参数用θ表示，估计量用表示

3.估计值：估计参数时计算出来的统计量的具体值

        如果样本均值x拔=80，则80就是μ估计值

二、评估统计量的标准

1.无偏性：估计量抽样分布的数学期望等于被估计的总体参数。设总体参数为θ，所选择的估计量为，如果E()=θ，则称θ为θ的无偏估计量

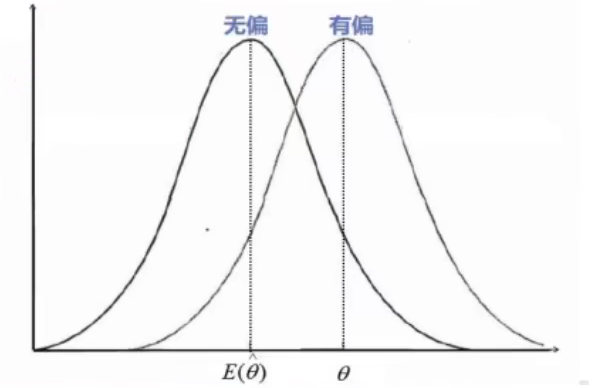
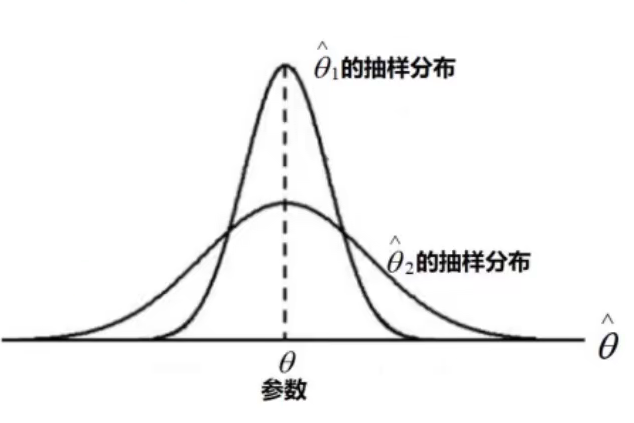
2.有效性：对同一总体参数的两个无偏点估计量，有更小标准差的估计量更有效

三、点估计 

1.用样本统计量 的某个取值直接作为总体参数θ的估计值

        比如用样本均值x拔直接作为总体均值μ的估计值；再比如，要估计一批产品的合格率，抽样结果合格率为96%，将96%直接作为此批产品合格率的估计值。

2.一个点估计的可靠性是由它的抽样标准误差来衡量的，这表明一个具体的点估计无法给出估计的可靠性的度量

四、区间估计

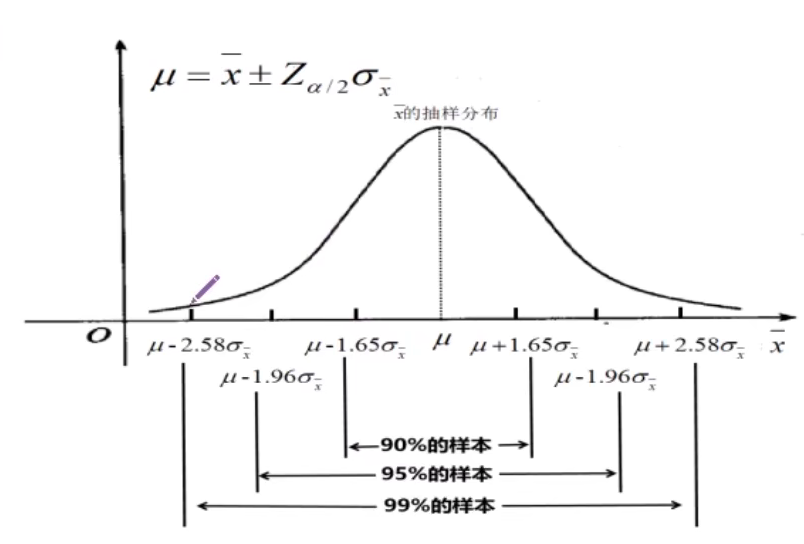
1.基本概念：a、在点估计的基础上，给出总体参数估计的一个区间范围，该区间由样本统计量加减估计误差而得到的。根据样本统计量的抽样分布能够对样本统计量与总体参数的接近程度给出一个概率度量。

比如：产品合格率在75%~85%之间，置信水平是95%

b、置信区间：在区间估计中，由样本统计量所构造的总体参数的估计区间称为置信区间，其中最小的值称为置信下限，最大值称为置信上限。统计学家在某种程度上确信这个区间包含真正的同一参数，所以给他取名置信区间。（其实就是误差范围，在抽样调查中，样本能在多大程度上代表总体）

c、置信水平：如果将构造的置信区间的步骤重复多次，置信区间包含的总体参数真值的次数所占的比例称为置信水平，也称置信度或置信系数。

        由100个样本构造的总体参数的100个置信区间中，由95%的区间包括总体参数的真值，有5%没包括，则95%这个值称为置信水平。（结果在误差范围之内的概率）