向量数据库的理论知识

什么是向量数据库

向量数据集是指由向量（也称为数组）组成的数据集。在机器学习和数据分析中，向量数据集通常用来表示一组特征或属性，每个向量代表一个数据点。这种数据集通常被用于训练机器学习模型，进行数据分析和模式识别等任务。向量数据集可以是一维的（包含一个特征）或多维的（包含多个特征），具体取决于具体的应用场景和数据结构。

向量数据库与传统数据库的区别在于数据类型。向量数据库专门用于存储向量数据。采用基于向量索引的存储方式，并支持基于向量相似度的查询。

而传统数据库可以存储各种类型的数据，采用关系型模型或其他存储方式，并支持各种查询语言

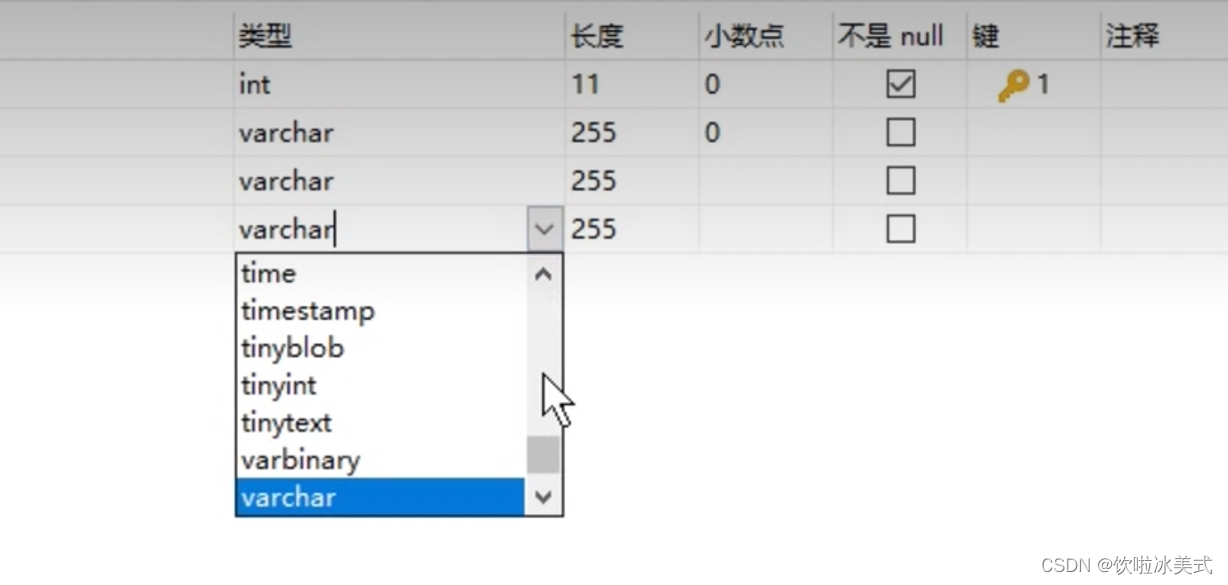
什么是向量

向量是指一组有序数值组成的对象。向量可以表示空间中的一个点或者某种属性的集合。

如二维向量（两个分量）、三维向量（三个分量）。

每个分量可以是任意实数或复数

举个例子：

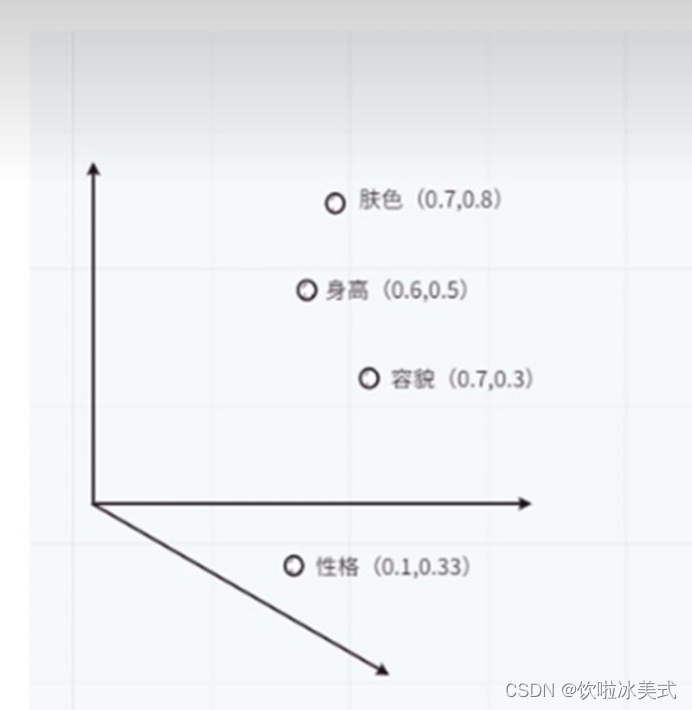
        以前主要通过打标记来识别物种。

        比如，给张三打上标记来识别他，标记是身高、肤色、容貌

       

如果张三有个双胞胎弟弟，只需要再加一个维度。维度和特征越多识别就越准确。

向量嵌入Vector embedding

        是将离散的对象或数据映射到连续的向量空间的过程。其中的向量叫做嵌入向量。

        在NLP中，向量嵌入通常用于表示单词、短语或句子。向量嵌入也是把对象转换成向量的过程。

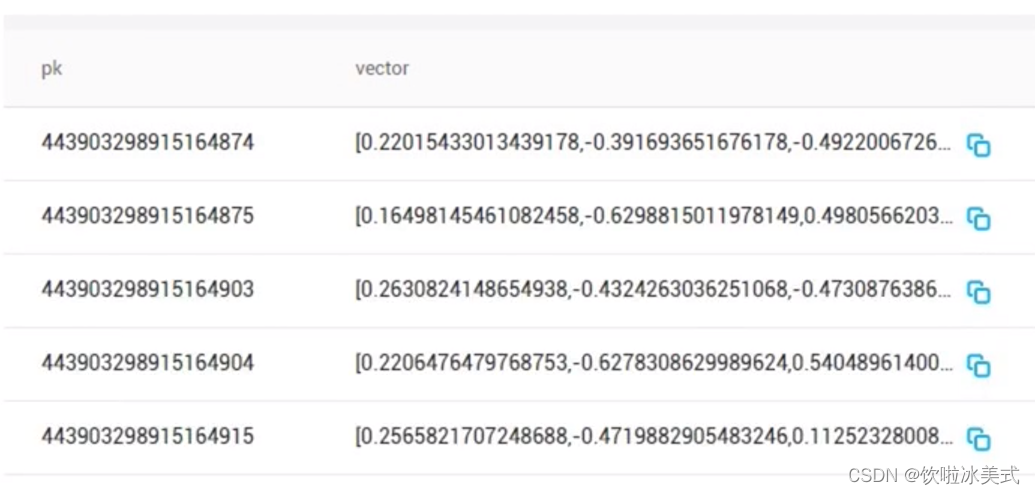
向量嵌入可以将数据的语义信息保留在向量空间中，因此向量数据库可以使用相似度度量来进行检索，从而实现基于语义的搜索。

向量搜索 Vector search

        一般对语料的搜索可以通过向量之间的距离来判断它们的相似度。

        如果需要搜索某个相似的想来是不是需要对库中的每个向量进行比较。但这种的计算量是非常巨大的，所以需要一种更加高效的算法来解决这个问题。

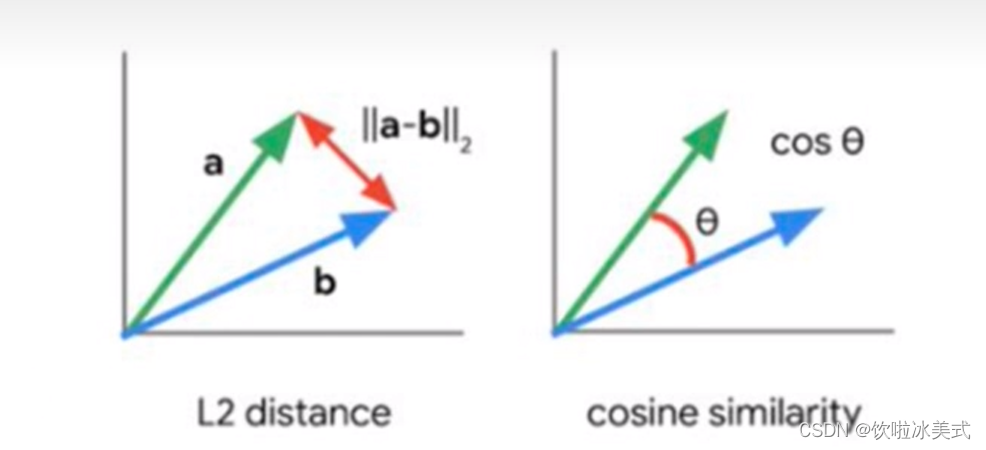
比较两个向量的相似的方法有很多

常见的有：

点积（dot product）：向量的点积相似度是指两个向量之间的点积值，它适用于许多实际场景。例如图像识别、语义搜索和文档分类等。但点积相似度算法对向量的长度敏感，因此在计算高维向度的相似性时可能会出现问题。

内积（inner product）：是一种计算向量之间相似度的度量算法。它计算两个向量之间的点积（内积），所得值越大越与搜索值相似。

欧式距离（L2）：直接比较两个向量得欧式距离，距离越近越相似。欧几里得算法的优点是可以反映向量的绝对距离，适用于需要考虑向量长度的相似性计算。例如推荐系统中，需要根据用户的历史行动来推荐相似的商品，这时就需要考虑用户的历史行为的数量而不仅仅是用户的历史行为的相似度。

余弦相似度（Cosine）：两个向量的夹角越小越相似，比较两个向量的余弦值进行比较。夹角越小，余弦值越大。余弦相似度对向量的长度不敏感，只关注向量的方向，因此适用于高维向量的相似性计算。对于比较向量，也会出现性能问题，尤其是海量的向量模型库中比较，那么就可以通过优化向量来提高搜索效率。

主要有两种方式：

1、减少向量大小--通过降维或减少表示向量值的长度 比如向量降维 压缩等。

2、缩小搜索范围--可以通过聚类或将向量组织成基于树形 图形结构来实现。并限制搜索范围仅在最接近的簇中进行。或者通过最相似的分支进行过滤。

 

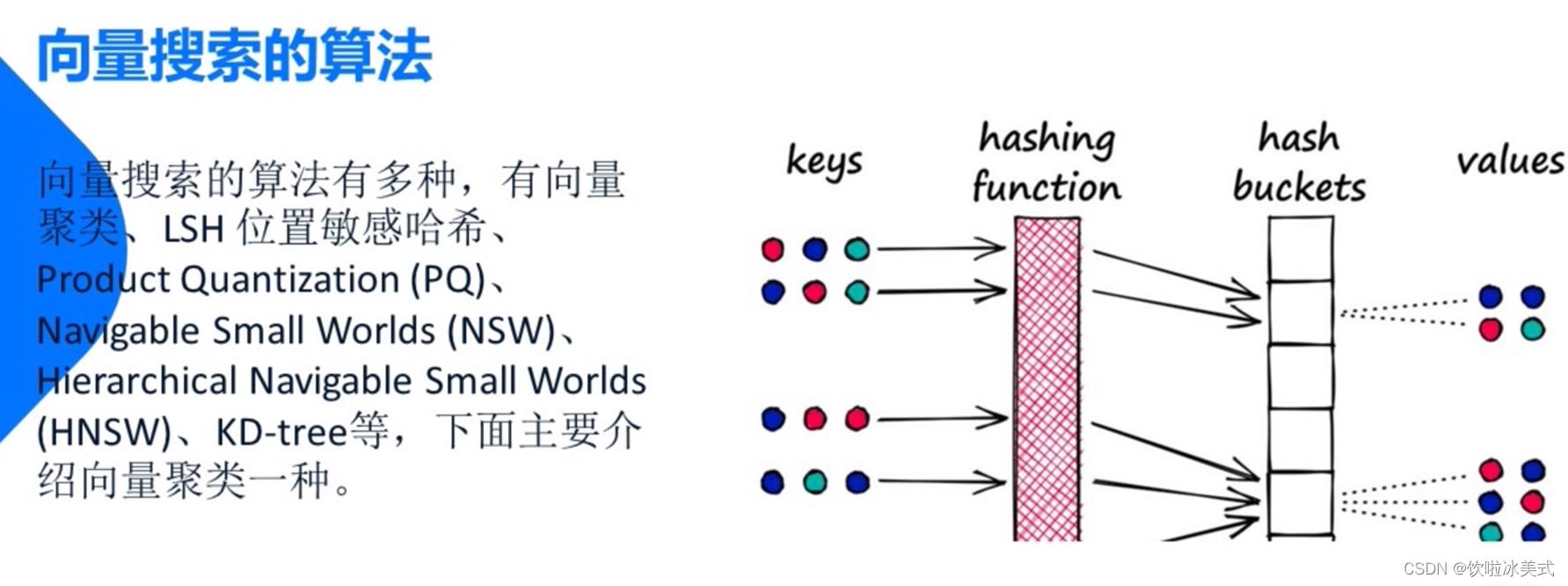
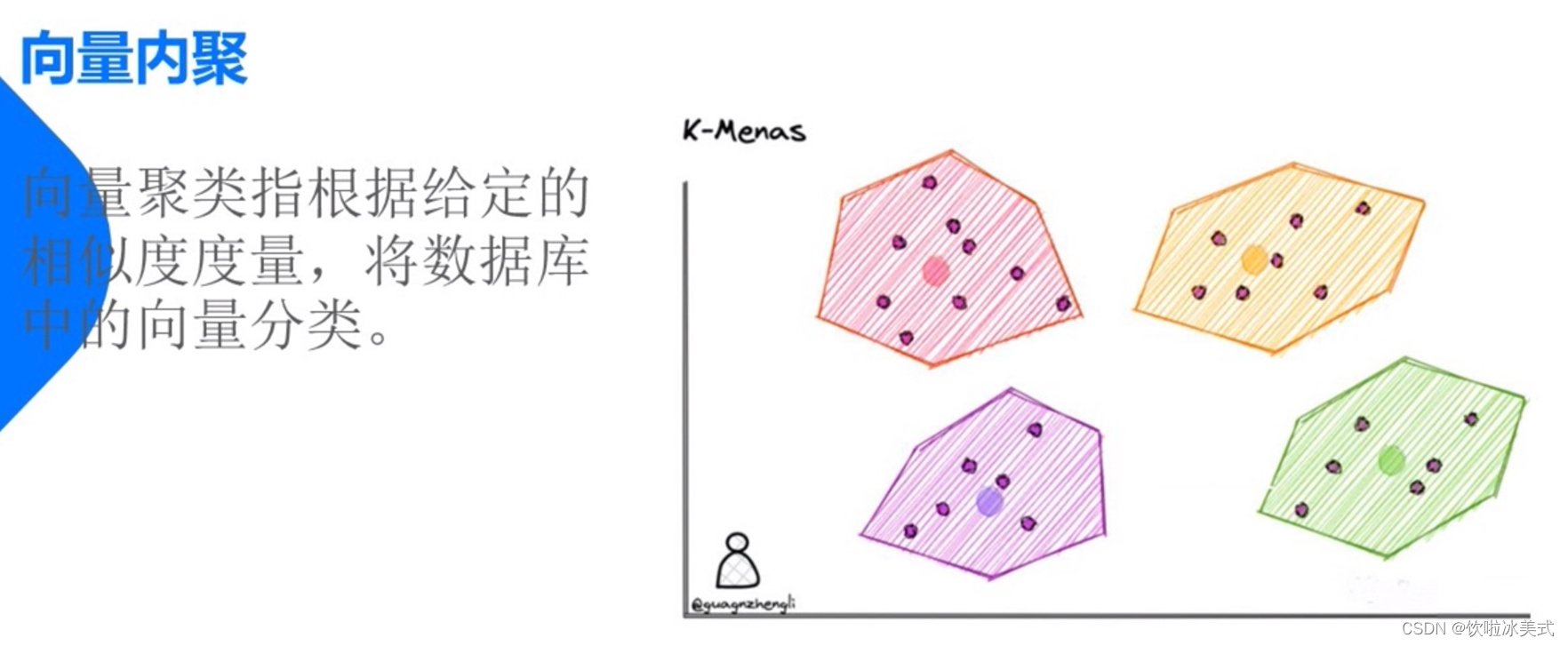
比如如果一枚戒指掉到大海，面对这么大的海域怎么找呢？

首先找到掉的大致范围

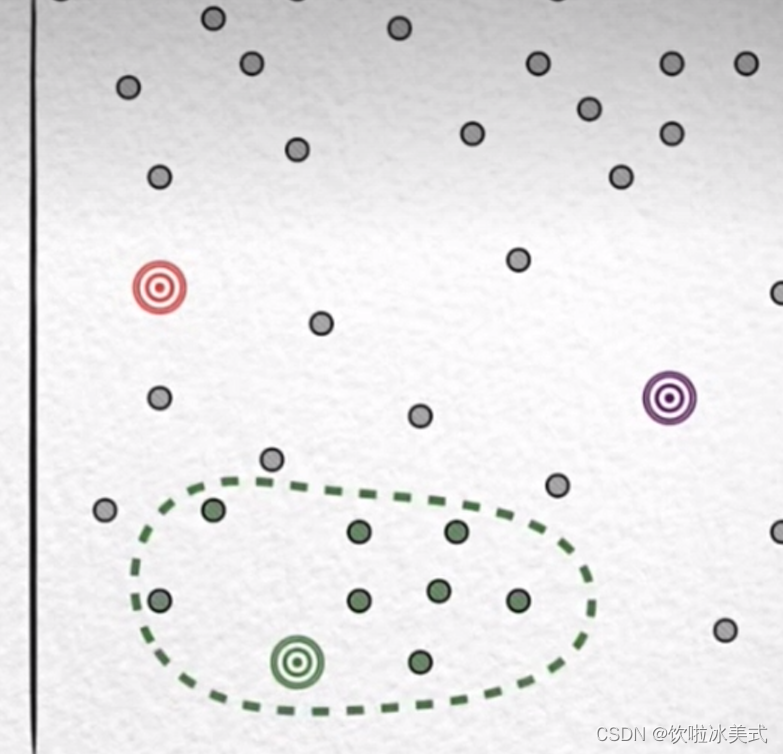
再找到有人造金属的海床，然后找到制造针的金属物质，最后在这对金属物质里找就相对容易点了。

找的过程也是一种内聚的过程。

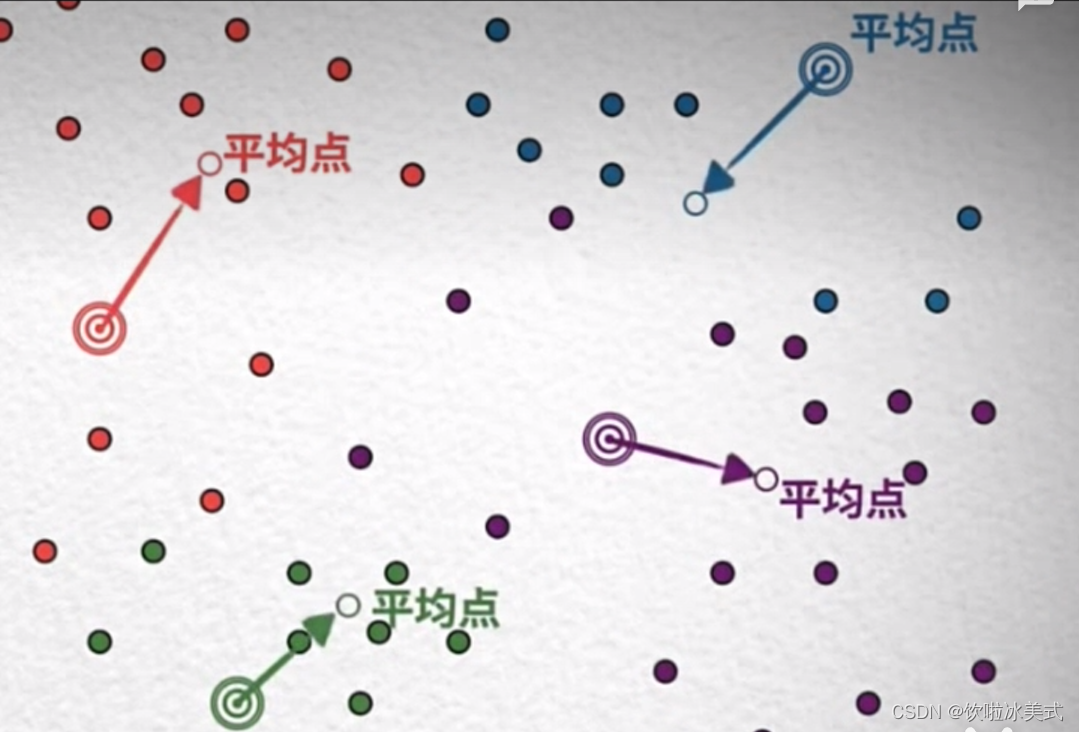
向量数据库应用场景（Vector Database Application Scenarios）

Elasticsearch数据库简单的向量操作，简称ES