P3369 【模板】普通平衡树（splay 算法）

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

1. 插入一个数 x。
2. 删除一个数 x（若有多个相同的数，应只删除一个）。
3. 定义排名为比当前数小的数的个数 +1。查询 x 的排名。
4. 查询数据结构中排名为 x 的数。
5. 求 x 的前驱（前驱定义为小于 x，且最大的数）。
6. 求 x 的后继（后继定义为大于 x，且最小的数）。

对于操作 3,5,6，不保证当前数据结构中存在数 x。

输入格式

第一行为 n，表示操作的个数,下面 n 行每行有两个数 opt 和 x，opt 表示操作的序号（1≤opt≤6）

输出格式

对于操作 3,4,5,6 每行输出一个数，表示对应答案。

输入输出样例

输入 #1复制

10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

输出 #1复制

106465
84185
492737

说明/提示

【数据范围】
对于 100% 的数据，1≤n≤105，∣x∣≤107

解析：

这时一个思维的跨度：

我们自己构造平衡二叉树，左儿子节点小于父节点，右儿子的全部节点大于父节点。

我们需要对二叉树进行左转和右转。

每次进行转动时替代其相对的儿子。

比如：

右旋时：x的右儿子当作y的左儿子。

这里你们可能会问为什么当y的左儿子呢？

答：因为这是一颗平衡二叉树，左儿子一定小于父节点。

而且x为y的左儿子，x的任意一个儿子一定小于其x的父节点。
左旋同理。

实现代码是用异或操作，刚好就是其儿子转动的对立面。比如：x右旋，x的右儿子为y,这时原本的x的右儿子就要当y的左儿子。这样子x的右儿子不会丢失。又满足平衡二叉树的性质。

实现左旋右旋代码如下：

void rotate(int x) // 可以进行左旋 和右旋 
{
	//先修 z ;在修 y ;在修 x的儿子节点;在修 x本身 
	int y = tr[x].fa,z = tr[y].fa, k = tr[y].ch[1] == x; // z -> y -> x  我们需要 将 它转为 z->x->y; 
	tr[z].ch[tr[z].ch[1] ==y]  = x, tr[x].fa = z; //  z的 儿子 为 y 替换为 x , 在将 x 的父节点 为 x
	tr[y].ch[k] = tr[x].ch[k^1];//比如如果 初始 y的左儿子为 x 当替换完。 y的左儿子空了 ,将x的右儿子给y的做儿子 
	tr[tr[x].ch[k^1]].fa = y; // 从x下的儿子 替换到 y 下时  ，儿子的父节点要变 
	tr[x].ch[k^1] = y;//这时x那个替换到 y的儿子空位了。
	tr[y].fa = x;
	pushup(y);//先push儿子在父节点 
	pushup(x); 
}

下面就是我们如何维护这个平衡二叉树的树高，尽可能使它的高度最小。

我学到的方法是， 当一棵树他是以直线型,折线型时，如下图所示：

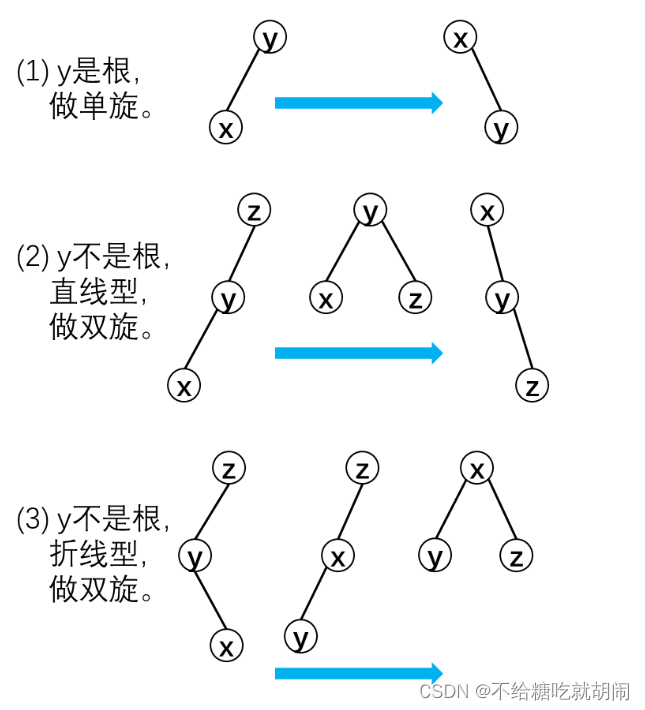
当直线型时，先旋转它的父节点，在旋转它自己本身。

当折线型时，先旋转它自己，在旋它自己。

代码如下：

void splay(int x,int k) //k为父节点 
{
	while(tr[x].fa != k)
	{
		int y = tr[x].fa,z = tr[y].fa;//从 x起 2个父节点  
		if(z != k){ // 如果 是 一条    有折线时 
		//如果 时一条 直线 时 1^1 为 false ,先选 y 在旋 x  
			(ls(y) == x)^(ls(z)==y) ? rotate(x):rotate(y);
		}
		rotate(x);
	}
	if(!k){//等于 0 的时候 才为 根节点 
		root = x;
	}
}

还有一个前驱操作：

先用find函数这个节点在那里。

在遍历它的左儿子的右儿子。到达最右的那个儿子。

后继也是一样。

void find(int v)
{
	int x = root;
	while(tr[x].ch[v > tr[x].v] && v!=tr[x].v)
	{
		x = tr[x].ch[v > tr[x].v];
	}
	splay(x,0);
}
 
int getpre(int v)
{
	find(v);
	int x = root;
	if(tr[x].v < v){
		return x;
	}
	x = ls(x);
	while(rs(x)){
		x = rs(x);
	}
	splay(x,0);
	return x;
}
 
int getsuc(int v)
{
	find(v);
	int x = root;
	if(tr[x].v > v) return x;
	x = rs(x);
	while(ls(x)) x = ls(x);
	splay(x,0);
	return x; 
}

删除操作：

我们找到它的前驱和后继，再进行把删除的点移到其后继的左儿子上，再进行删除操作。

这个需要画图理解一下。

void del(int v)//删除 
{
	int pre = getpre(v);
	int suc = getsuc(v);
	splay(pre,0);
	splay(suc,pre);//将它转到左节点方便删除
	int del = tr[suc].ch[0];
	if(tr[del].cnt > 1)
	{
		tr[del].cnt--;
		splay(del,0);	
	} 
	else{
		tr[suc].ch[0] = 0;
		splay(suc,0);
	}
}

刚开始插入操作时，我们要进行哨兵的插入。

完整代码如下：

#include<bits/stdc++.h>
using namespace std;
 
#define ls(x) tr[x].ch[0]
#define rs(x) tr[x].ch[1]
const int N = 1100010,INF = (1<<30)-1;
struct node{
	int ch[2];
	int fa;
	int v;
	int cnt;
	int siz;
	void init(int p,int v1){
		fa = p;
		v = v1;
		cnt = siz  = 1;
	}
}tr[N];
int root = 0,tot = 0;
void pushup(int x)
{
	tr[x].siz = tr[ls(x)].siz + tr[rs(x)].siz + tr[x].cnt;
}
 
void rotate(int x) // 可以进行左旋 和右旋 
{
	//先修 z ;在修 y ;在修 x的儿子节点;在修 x本身 
	int y = tr[x].fa,z = tr[y].fa, k = tr[y].ch[1] == x; // z -> y -> x  我们需要 将 它转为 z->x->y; 
	tr[z].ch[tr[z].ch[1] ==y]  = x, tr[x].fa = z; //  z的 儿子 为 y 替换为 x , 在将 x 的父节点 为 x
	tr[y].ch[k] = tr[x].ch[k^1];//比如如果 初始 y的左儿子为 x 当替换完。 y的左儿子空了 ,将x的右儿子给y的做儿子 
	tr[tr[x].ch[k^1]].fa = y; // 从x下的儿子 替换到 y 下时  ，儿子的父节点要变 
	tr[x].ch[k^1] = y;//这时x那个替换到 y的儿子空位了。
	tr[y].fa = x;
	pushup(y);//先push儿子在父节点 
	pushup(x); 
}
 
void splay(int x,int k) //k为父节点 
{
	while(tr[x].fa != k)
	{
		int y = tr[x].fa,z = tr[y].fa;//从 x起 2个父节点  
		if(z != k){ // 如果 是 一条    有折线时 
		//如果 时一条 直线 时 1^1 为 false ,先选 y 在旋 x  
			(ls(y) == x)^(ls(z)==y) ? rotate(x):rotate(y);
		}
		rotate(x);
	}
	if(!k){//等于 0 的时候 才为 根节点 
		root = x;
	}
}
 
void insert(int v) //插入 节点  
{
	int x = root,p = 0;
	while(x&& tr[x].v != v){ // 弹出 条件 x 为 0节点 找不到  或者 找到当前节点  
		p = x, x = tr[x].ch[v > tr[x].v];
	}
	
	if(x) {
		tr[x].cnt++;
	}
	else{ // 新创建 一个节点 
		x = ++tot;
		tr[p].ch[v>tr[p].v] = x;
		tr[x].init(p,v); 
	}
	splay(x,0);
}
 
 
void find(int v)
{
	int x = root;
	while(tr[x].ch[v > tr[x].v] && v!=tr[x].v)
	{
		x = tr[x].ch[v > tr[x].v];
	}
	splay(x,0);
}
 
int getpre(int v)
{
	find(v);
	int x = root;
	if(tr[x].v < v){
		return x;
	}
	x = ls(x);
	while(rs(x)){
		x = rs(x);
	}
	splay(x,0);
	return x;
}
 
int getsuc(int v)
{
	find(v);
	int x = root;
	if(tr[x].v > v) return x;
	x = rs(x);
	while(ls(x)) x = ls(x);
	splay(x,0);
	return x; 
}
 
void del(int v)//删除 
{
	int pre = getpre(v);
	int suc = getsuc(v);
	splay(pre,0);
	splay(suc,pre);//将它转到左节点方便删除
	int del = tr[suc].ch[0];
	if(tr[del].cnt > 1)
	{
		tr[del].cnt--;
		splay(del,0);	
	} 
	else{
		tr[suc].ch[0] = 0;
		splay(suc,0);
	}
}
 
int getrank(int v)
{
	insert(v);
	int res = tr[tr[root].ch[0]].siz;
	del(v);
	return res;
}
 
int getval(int k) //第k个值 
{
	int x = root;
	while(true)
	{
		if(k <= tr[ls(x)].siz) x = ls(x);
		else if(k <= tr[ls(x)].siz + tr[x].cnt) break;
		else k -= tr[ls(x)].siz + tr[x].cnt,x = rs(x);
	}
	splay(x,0);
	return tr[x].v;
}
 
 
int main()
{
	insert(-INF);//加入哨兵 
	insert(INF);
	int n,op,x;
	scanf("%d",&n);
	while(n--)
	{
		scanf("%d%d",&op,&x);
		if(op == 1){
			insert(x); 
		}
		else if(op == 2){
			del(x);
		}
		else if(op == 3)
		{
			printf("%d\n",getrank(x));
		}else if(op == 4){
			printf("%d\n",getval(x+1)); //因为有哨兵 
		}else if(op == 5)
		{
			printf("%d\n",tr[getpre(x)].v);
		}else{
			printf("%d\n",tr[getsuc(x)].v);
		}
	}
	return 0;	
}  

时间复杂度为：O（n*logn)