第十三届蓝桥杯大赛C++研究生组 试题B：超级质数_一行,给出一个整数 x (1≤x≤10 9 )output第一行,一个整数 k,表示 x 以内超级素

---

前言

提示：本系列所有相关代码都以C++为编程语言进行讲解。

本文为第十三届蓝桥杯软件赛省赛第二场C++研究生组的题目，会依次对每道题进行总结记录，能力有限，如有更优解法，还请不吝赐教。

---

题目

如果一个质数 P 的每位数字都是质数，而且每两个相邻的数字组成的两位
数是质数，而且每三位相邻的数字组成的三位数是质数，依次类推，如果每相
邻的 k 位数字组成的 k 位数都是质数，则 P 称为超级质数。
如果把超级质数 P 看成一个字符串，则这个超级质数的每个子串都是质
数。
例如，53 是一个超级质数。
请问，最大的超级质数是多少？

解题思路

本题对超级质数的定义为，该数的每个子串都是质数，例如

数字2375
那么该数字的子串为：2、3、7、5、23、37、75、237、375、2375
当以上子串全部都是质数时，则该数为超级质数。

那么解题步骤如下

1. 寻找1到n中的质数
2. 从得到的质数中，求出该数的全部子串
3. 依次判断全部子串，如果出现某一子串不为质数，则返回步骤1寻找下一个质数。

一、寻找质数

判断一个数是不是质数，常规方法是判断该数字能否被比自己小的数字整除。
代码如下：

bool Prime_Number_Judge(const int &num)
{
	if (num <= 3) //判断是否小于3
	{
		return num > 1;
	}
	for (size_t i = 2; i < num; i++)//判断能否被小于自身的数整除
	{
		if (num % i == 0)
		{
			return false;
		}
	}
	return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

然而事实上，如果一个数不是质数，一定存在某个约数，分别大于sqrt(num)和小于sqrt(num)，那么我们只需要判断该数是否能被小于sqrt(num)的数整除整除。

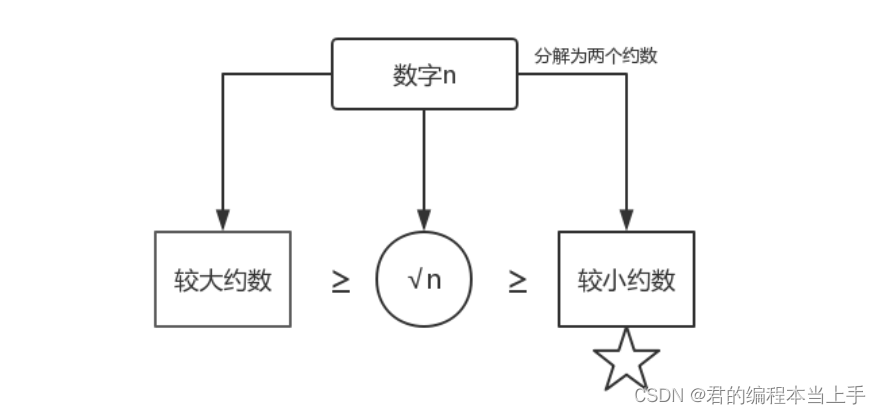
则代码改为如下：

bool Prime_Number_Judge(const int &num)
{
	if (num <= 3) //判断是否小于3
	{
		return num > 1;
	}
	for (size_t i = 2; i < sqrt(num); i++)//判断能否被小于sqrt(num)的数整除
	{
		if (num % i == 0)
		{
			return false;
		}
	}
	return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

一个数字如果不能被2整除，那么一定不能被其他偶数整除，因为任意一个偶数都可以被分2*n。那么我们只需要判断能否被小于sqrt(num)的奇数整除即可
代码优化为：

bool Prime_Number_Judge(const int &num)
{
	if (num <= 3) //判断是否小于3
	{
		return num > 1;
	}
	if ( num % 2 == 0 )//判断能否可以被2整除
	{
		return false;
	}
	for (size_t i = 3; i < sqrt(num); i+=2)//判断能否被小于sqrt(num)的奇数整除
	{
		if (num % i == 0)
		{
			return false;
		}
	}
	return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

再者对于大于5的质数一定是6X-1或者6X+1的。利用这种特性。可以对整数进行筛选，只判断那些是6x-1或6x-1的整数是否为质数。

证明：
令x≥1，则大于等于5的自然数表示如下：······6x-1，6x，6x+1，6x+2，6x+3，6x+4······（相邻6个数为一组）
6x、6x+2、6x+4可以被2 整除，6x+3可以表示为3*(2x+1)，即可以被3整除，只剩下6x-1和6x+1中可能存在质数。因此质数一定是6x-1或6x+1。

代码优化如下：

bool Prime_Number_Judge(const int &num)
{
	if (num <= 3) //判断是否小于3
	{
		return num > 1;
	}
	if (num % 6 != 1 && num % 6 != 5)//判断是否为6x-1或6x+1
	{
		return false;
	}
	if ( num % 2 == 0 )//判断能否可以被2整除
	{
		return false;
	}
	for (size_t i = 3; i < sqrt(num); i+=2)//判断能否被小于sqrt(num)的奇数整除
	{
		if (num % i == 0)
		{
			return false;
		}
	}
	return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

二、找出全部子串

分为三步
1、求出数字共有几位，如：1即有1位，53即有2位，2373即有4位

//求一个数字有几位
int& Get_Number_Size(const int &num)
{
	int digit = 0;
	int val = num;
	while (val)
	{
		val /= 10;
		digit++;
	}
	return digit;
}
1
2
3
4
5
6
7
8
9
10
11
12

2、将数字的每位数字分别用数组表示，如2372，则建立数组[2,3,7,3]

vector<int>& Get_Digits(const int &num , vector<int> &digits)
{
	//将数字的每位数字分别用数组表示
	int vactor_val = 0;
	//利用Get_Number_Size()求得数字有几位，并进行求余和整除计算
	for (size_t num_size = Get_Number_Size(num); num_size > 0; num_size--)
	{
		vactor_val = num % (int)pow(10.0, num_size);
		vactor_val = vactor_val /(int)pow(10.0, num_size - 1);
		digits.push_back(vactor_val);
	}
	return digits;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

3、利用循环求出数字的各个子串

vector<int>& Get_K_Adjacent(const int &num, vector<int> &adjacent)
{
	vector<int> digists_number; 
	//数字的每位数字分别用数组表示，存在数组digists_number
	Get_Digits(num , digists_number); 
	//求出数字长度
	int digits = Get_Number_Size(num);
	for (size_t i = 0; i < digits; i++)
	{
		for (size_t j = 0; j < digits-i ; j++)
		{
			string buf;
			int k = 0;
			while (k <= i)
			{
				//用字符串的+=操作符进行子串的拼接
				buf += to_string(digists_number.at(j + k));
				k++;
			}
			//再将拼接的子串转为整数，存在数组adjacent
			adjacent.push_back(stoi(buf));
		}
	}
	return adjacent;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

三、依次判断全部子串，如果出现某一子串不为质数，则返回步骤1寻找下一个质数。

至此全部工作已经完成，利用for循环依次进行遍历数字，寻找质数中的超级质数即可。
全部代码如下：

#include <iostream>
#include <string>
#include <vector>
using namespace std;

//判断一个数是否为质数，是则返回true，不是返回false
bool Prime_Number_Judge(const int &num)
{
	if (num <= 3) //判断是否小于3
	{
		return num > 1;
	}
	if (num % 6 != 1 && num % 6 != 5)//判断是否为6x-1或者6x+1
	{
		return false;
	}
	if (num % 2 == 0)//判断能否被2整除
	{
		return false;
	}
	for (size_t i = 3; i < sqrt(num); i += 2)//判断能否被小于自身的数整除
	{
		if (num % i == 0)
		{
			return false;
		}
	}
	return true;
}

//求一个数字有几位
int& Get_Number_Size(const int &num)
{
	int digit = 0;
	int val = num;
	while (val)
	{
		val /= 10;
		digit++;
	}
	return digit;
}

//将一个数的所有位数返回出来
vector<int>& Get_Digits(const int &num , vector<int> &digits)
{
	int vactor_val = 0;
	//利用Get_Number_Size()求得数字有几位，并进行求余和整除计算
	for (size_t num_size = Get_Number_Size(num); num_size > 0; num_size--)
	{
		vactor_val = num % (int)pow(10.0, num_size);
		vactor_val = vactor_val /(int)pow(10.0, num_size - 1);
		digits.push_back(vactor_val);
	}
	return digits;
}

//求出全部子串
vector<int>& Get_K_Adjacent(const int &num, vector<int> &adjacent)
{
	vector<int> digists_number;
	//数字的每位数字分别用数组表示，存在数组digists_number
	Get_Digits(num , digists_number);
	int digits = Get_Number_Size(num);
	for (size_t i = 0; i < digits; i++)
	{
		for (size_t j = 0; j < digits-i ; j++)
		{
			string buf;
			int k = 0;
			while (k <= i)
			{
				//用字符串的+=操作符进行子串的拼接
				buf += to_string(digists_number.at(j + k));
				k++;
			}
			//再将拼接的子串转为整数，存在数组adjacent
			adjacent.push_back(stoi(buf));
		}
	}
	return adjacent;
}

int main()
{
	//依次检查1-10000是否为素数
	for (size_t i = 1; i < 10000; i++)
	{
		if (Prime_Number_Judge(i))
		{
			//在得出的素数中进行超级素数的检查
			vector<int> buf;
			Get_K_Adjacent(i, buf);
			//sign作为标记，标记是否子串中有非质数，如果有则置为0
			int sign = 1;
			for (size_t j = 0; j < buf.size(); j++)
			{
				if (!Prime_Number_Judge(buf.at(j)))
				{
					//出现非质数，标记置为0
					sign = 0;
					break;
				}
			}
			if (sign)
			{
				cout << i << "is super_prime_number" << endl;
			}
		}
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112

最终运行结果为：

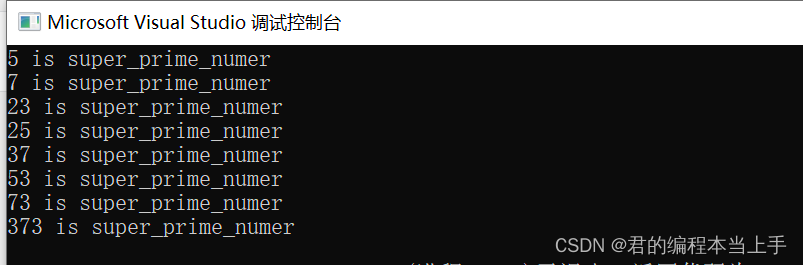
故本题答案为373。恭喜完成第一道题！

注：

关于寻找质数的思路参考来自博主：是杰夫呀 的文章，链接在这里，原文有更详细的解说