《机器学习》之 朴素贝叶斯原理及代码解析_朴素贝叶斯代码解析

1 介绍

朴素贝叶斯 (Naive Bayes) 是贝叶斯分类算法中最简单的一个，一般用于处理二分类或多分类任务。该算法围绕着一个核心进行展开：贝叶斯定理。本文会从易于理解的角度对朴素贝叶斯的原理进行介绍，然后是代码实现，以加深对算法的理解。

2 原理

2.1 贝叶斯定理

首先看一下算法的核心，贝叶斯定理。
定理由来：
对于事件A与事件B, 有条件概率公式：
因为 P(AB) = P(BA) , 所以:

将 P(A) 除到左边，即得到贝叶斯定理：

贝叶斯定理有什么用呢？
一般对于 P(B|A) 难以计算时，会利用贝叶斯定理，将计算转换成对 P(A|B)、P(B)、P(A)的计算。

2.2 朴素贝叶斯算法

那么如何将朴素贝叶斯用于实际的分类任务呢？将贝叶斯定理中的事件A看作特征，将事件B看作类别，即得到以下形式：

其中，左式 P(类别|特征) 的含义是：在指定特征的情况下，某一类别出现的概率。就相当于在知道某样本各个特征的情况下，计算该样本属于每个类别的概率。如果能计算出这个概率值，取最大概率对应的类别作为样本的预测类别就行了。

那么 P(类别|特征) 好不好求呢？答案是否定的。此时就可以利用朴素贝叶斯公式将 P(类别|特征) 的计算转换成 P(特征|类别)、P(类别)、P(特征)的计算，这三个概率值是比较容易计算的，在训练样本的特征及类别上进行统计即可得到。

在实际的分类任务中，特征通常不只一个，即：

计算这个概率值时，如果直接去统计在某一类别的条件下，同时符合这些特征的样本个数，然后再相除，得到的概率结果会非常小。因为同时符合这些特征的样本个数非常少，所以朴素贝叶斯算法将这个概率拆分成多个条件概率的累乘。

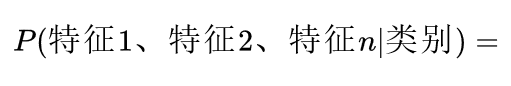
朴素贝叶斯算法假设各个特征是相互独立的，所以可以将概率拆分成多个条件概率累乘。这也是算法名称中朴素二字的由来，该算法需要预先假设样本各个特征之间相互独立。
同理，分母 P(特征) 也可拆分计算。

此时，P(类别|特征) 就很容易计算了。

需要注意的问题：
1 特征太多时，多个小于1的概率值累乘可能会造成下溢出，可以将使用 log 计算将累乘转换成累加，避免下溢出。
2 如果某一类别下特征m没有出现，此时 P(特征m|类别)=0, 这会造成最终的概率值为0, 所以可使用贝叶斯平滑，就是在分子分母分别加1，可避免0概率出现的情况。在样本量充足的情况下，平滑不会对结果产生影响。

3 总结

优点：
1 不同于线性模型，朴素贝叶斯基于统计而不是基于权重的迭代优化，逻辑简单，容易实现；
2 分类过程的时间与空间复杂度都比较小。

缺点：
1 只能处理分类任务，并且只在样本特征较少的情况下，分类效果最好；
1 特征之间相互独立的假设在实际中通常是不成立的，在特征间相关性较大时或者特征数量较多时效果不好。

4 代码实践

理解算法的最好做法就是用代码实现它。在下面代码中，我加入了充分的注释以易理解。

import numpy as np
import pandas as pd

class NaiveBayes(object):
    def __init__(self, X_train, y_train):
        self.X_train = X_train	#样本特征
        self.y_train = y_train	#样本类别
        #训练集样本中每个类别(二分类)的占比，即P(类别)，供后续使用
        self.P_label = {1: np.mean(y_train.values), 0: 1-np.mean(y_train.values)}

    #在数据集data中, 特征feature的值为value的样本所占比例
    #用于计算P(特征|类别)、P(特征)
    def getFrequency(self, data, feature, value):
        num = len(data[data[feature]==value]) #个数
        return num / (len(data))

    def predict(self, X_test):
        self.prediction = [] #预测类别
        # 遍历样本
        for i in range(len(X_test)):
            x = X_test.iloc[i]      # 第i个样本
            P_feature_label0 = 1    # P(特征|类别0)之和
            P_feature_label1 = 1    # P(特征|类别1)之和
            P_feature = 1           # P(特征)之和
            # 遍历特征
            for feature in X_test.columns:
                # 分子项，P(特征|类别)
                data0 = self.X_train[self.y_train.values==0]  #取类别为0的样本
                P_feature_label0 *= self.getFrequency(data0, feature, x[feature]) #计算P(feature|0)

                data1 = self.X_train[self.y_train.values==1]  #取类别为1的样本
                P_feature_label1 *= self.getFrequency(data1, feature, x[feature]) #计算P(feature|1)

                # 分母项，P(特征)
                P_feature *= self.getFrequency(self.X_train, feature, x[feature])
	
			#属于每个类别的概率
            P_0 = (P_feature_label0*self.P_label[0]) / P_feature
            P_1 = (P_feature_label1 * self.P_label[1]) / P_feature
            #选出大概率值对应的类别
            self.prediction.append([1 if P_1>=P_0 else 0])
        return self.prediction
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

使用测试：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

#加载数据
X, y = load_iris(return_X_y=True)
X, y = pd.DataFrame(X[:100]), pd.DataFrame(y[:100])
#训练集、测试集划分
X_train, X_test, y_train, y_test =  train_test_split(X, y, test_size=0.3)

model = NaiveBayes(X_train, y_train)	#训练
y_pre = model.predict(X_test)			#预测
print(accuracy_score(y_pre, y_test))  	#评分：0.8
1
2
3
4
5
6
7
8
9
10
11
12
13

如果觉得有收获，就请点个赞吧~
万分感谢！