- 1矿渣玩客云刷机armbian教程及使用(新手上路篇)
- 2chatGPT流式输出的几种方式
- 3思维探索者:我们需要演绎与归纳
- 4Python 集合(set) remove() 方法_python set()函数 remove
- 5MMDetection实验记录踩坑记录_mmdetection训练自己数据集的ap值为0
- 6Linux安装python3环境,并更换pip国内源_linux更换python3源
- 7数据可视化(词云图)_flask词云图
- 8creo工程图模板_ProE&Creo出工程图不是梦,一文助你彻底搞懂绘图属性设置
- 9JSON与XML的区别_json和xml比较
- 10手把手带你YOLOv5/v7 添加注意力机制_yolo 形状注意力
LDA主题模型详解
赞
踩
1.什么是LDA主题模型
LDA(Latent Dirichlet Allocation)是一种文档生成模型。它认为一篇文章是有多个主题的,而每个主题又对应着不同的词。一篇文章的构造过程,首先是以一定的概率选择某个主题,然后再在这个主题下以一定的概率选出某一个词,这样就生成了这篇文章的第一个词。不断重复这个过程,就生成了整片文章。当然这里假定词与词之间是没顺序的。
LDA的使用是上述文档生成的逆过程,它将根据一篇得到的文章,去寻找出这篇文章的主题,以及这些主题对应的词。
现在来看怎么用LDA,LDA会给我们返回什么结果。
2.主题分布与词分布
上面说了,一篇文章的生成过程,每次生成一个词的时候,首先会以一定的概率选择一个主题。不同主题的概率是不一样的,在这里,假设这些文章-主题符合多项式分布。同理,主题-词也假定为多项式分布。所谓分布(概率),就是不同情况发生的可能性,它们符合一定的规律。
两点分布
已知随机变量X的分布率为
| X | 1 | 0 |
|---|---|---|
| p | p | 1-p |
则有
抛一次硬币的时候,不是正面就是反面,符合两点分布。这里概率P为参数
二项分布
二项分布,即是重复n次两点分布。设随机变量X服从参数为n,p的二项分布。其中,n为重复的次数,p为两点分布中,事件A发生的概率。设X=k为n次实验中事件A发生了k次的概率。可以得到X的分布率为:
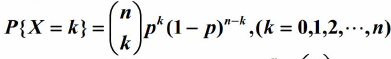
例如,丢5次硬币,事件A为硬币正面朝上,则表示求抛5次硬币,有k次硬币正面朝上的概率。通过计算可以得知二项分布的期望和方差如下,这里就不计算了:
多项式分布
多项式分布(multinomial)是二项分布在两点分布上的延伸。在两点分布中,一次实验只有两种可能性,p以及 (1-p)。例如抛一枚硬币,不是正面就是反面。在多项式分布中,这种可能的情况得到了扩展。例如抛一个骰子,一共有6种可能,而不是2种。
设某随机实验如果有k个可能情况 A1、A2、…、Ak,分别将他们的出现次数记为随机变量X1、X2、…、Xk,它们的概率分布分别是p1,p2,…,pk,那么在n次采样的总结果中,A1出现n1次、A2出现n2次、…、Ak出现nk次的这种事件的出现概率P有下面公式:
这里,p1,p2…pk都是参数
那么现在我们回到LDA身上,前面已经说了主题和词是符合多项分布的,我们可以用骰子形象地表达一篇文章的生成的过程。
有两类骰子,一种是文章-主题(doc-topic)骰子,骰子的每面代表一种主题。这里设一共有K个主题,则K面。骰子的各个面的概率记为
ϑ⃗ =(p1,p2,p3,...,pk)
。各个面的概率即为这个多项式分布的参数。另一种骰子为主题-词(topic-word)骰子,一共有K个,从1~K编号,分别对应着不同的主题。骰子的一个面代表一个单词。由于有K个骰子,把不同主题-词骰子各个面的概率分别记为
φ⃗ 1,φ⃗ 2,...φ⃗ k
一个主题-词骰子,他的各个面的概率即为这个多项式分布的参数。那么一篇文章的生成过程可以表示为:
- 抛掷这个doc-topic骰子,得到主题编号z
- 选择编号为z的topic-word骰子,得到词w
- 不断重复步骤1以及步骤2
3.参数估计
上面我们已经知道了主题分布和词分布都属于多项式分布,只是它们的参数究竟是什么值,我们还无从知晓。如果我们能估算出它们的参数,我们就能求得这些主题分布和词分布。LDA的主要目的就是求出主题分布和词分布,距离这个目的,我们近在咫尺。
极大似然估计
我们知道,频率可以用来估计参数。例如对于两点分布,抛硬币。当我们抛的次数足够多,可以估出p接近1/2,大数定理是有力的保证。频率学派为参数估计提供了另一种有力的工具——极大似然估计。它的思想可以这样形象地表达:既然样本已经出来了,我们有理由相信它们发生的概率很大,于是我们不如就设给定参数的情况下,出现这些样本的概率是最大的,通过求导计算极值,从而计算出参数。
在这里,我们的样本就是我们观察到的,文章d,以及文章里的词w。要求参数,我们可以写出如下式子:
p(wj|dm)=∑k=1Kp(wj|zk)p(zk|dm)
给定第m篇文章情况下,第i个词出现的概率正式上式。这里z主题是隐变量,我们观测不到,但把它暴露了出来。p(wj|zk)是词分布。p(zk|dm)是主题分布,也是我们要求的参数:φkj表示第k个主题词wj出现的概率;ϑmk表示第m篇文章主题k出现的概率。这样我们就可以求他们了。
我们设词和词,文章和文章之间是独立的。进一步,有了一个单词的概率,我们就可以求一篇文章的概率:
p(w⃗ |dm)=∏j=1n∑k=1Kp(wj|zk)p(zk|dm)
进一步,有了整个语料库(训练集,多篇文章)的概率:
L=∏m=1M∏j=1n∑k=1Kp(wj|zk)p(zk|dm)
上面说过,极大似然估计就是要让这个式子达到最大值。接下来还需要把式两边取对手,求导,解似然方程,就可以得到参数。实际上,到这里为止,讲述的是其实还只是plsa模型,因此这里不写出求解过程。LDA在plsa的求参上作了一些变化,下面将会讲到。
形式化地,似然函数可以如下表示:
P(x1,x2,...xn|ϑ)
哪个参数能够使得这个P最大,则把这个参数作为我们选定的参数。
贝叶斯估计
上一小节中我们知道,plsa模型用频率学派来估计主题分布和词分布的参数,频率学派认为参数是一个定值。而贝叶斯学派则认为参数是变化的,也应该符合一定的分布。LDA在plsa的基础上引入了贝叶斯学派的方式。
我们先来看看贝叶斯公式
P(ϑ|x)=P(x,ϑ)P(x)=P(x|ϑ)P(ϑ)P(x)
我们看看每个部分的含义:
P(θ):θ发生的概率,先验概率。
P(θ|x):在数据x的支持下,θ发生的概率,后验概率。
P(x|θ):似然函数,前面已经提及。
百度百科对先验后验有如下解释:
先验概率不是根据有关自然状态的全部资料测定的,而只是利用现有的材料(主要是历史资料)计算的;后验概率使用了有关自然状态更加全面的资料,既有先验概率资料,也有补充资料;
贝叶斯学派的思路很直观,就是如果只做了少量试验来估计参数(如均值或概率p),会由于小样本数据而造成估计不准。但利用之前已经拥有的经验(以前做过的试验数据),就可以让估计更为合理。
那么在给定样本X的情况下,要如何去修正参数P(ϑ|x)呢?类似极大似然函数那样,我们可以选择另P(θ|x)最大的θ,由于样本X是给定的,因此P(X)是不变的,由此有:
P(ϑ|x)∝P(x|ϑ)P(ϑ)
共轭先验分布
回到我们的LDA上,通过贝叶斯学派的观点对plsa模型进行改造。参数也是服从一定的分布的。原本绿色骰子(doc-topic分布)是P(θ)先验概率,现在成了P(θ|x)后验概率。词分布也是同样的。我们已经知道,主题分布以及词分布式服从多项式分布的。那么他们的参数要服从什么分布呢?我们知道,P(ϑ|x)∝P(x|ϑ)P(ϑ),而P(θ|x)服从多项式分布,因此P(θ)P(x|θ)归一化后也要服从多项式分布。
在贝叶斯概率理论中,有这么一种定义,如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律,那么先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
那么,我们就可以选择似然函数P(x|θ)的共轭先验作为P(θ)的分布。而Dirichlet分布正是多项式分布的共轭先验概率分布。
Dirichlet分布的更多说明和数学推导可以参考篇尾参考资料里的LDA数学八卦以及LDA漫游指南。这里叙述共轭先验分布一些后面要用到的特性。
Dir(p⃗ |α⃗ )+MultCount(m⃗ )=Dir(p⃗ |α⃗ +m⃗ )
对应贝叶斯参数估计的过程:先验分布+数据的知识=后验分布
MultCount是什么我们还没说到,但是根据式子可以知道它们对应我们观测到的样本数据。我们似乎还没讲到这些样本数据要如何组织,如何使用。举一个例子:
假设语料库中所有词的总数是N,如果我们关注每个词vi的发生次数ni,那么n⃗ =(n1,n2...nv)正好是一个多项分布

这就是MultCount。
对应到LDA中,文章-主题分布的MultCount是每个主题的词的总数。主题-词对应的是词分布里每个单词的计数。
最后,我们通过共轭先验分布来求参数的后验分布:有了分布,就可以使用(a)式用平均值来估计参数的值,可以通过计算分布的极值或者期望来作为我们选择的参数。
如果p⃗ ∼Dir(t⃗ |α⃗ ),有期望

于是有:

ni是词频的计数,对应到主题分布和词分布就是每个主题的词的总数/词分布里每个单词的计数。成为先验分布的伪计数。可以看到它的物理意义很直观,就是先验的伪计数+数据样本的计数占整体计数的比重。
有了参数的形式,对它的求解,可以使用变分EM以及吉布斯(Gibbs Sampling)的方式。在下一篇文章中,将给出吉布斯采样的原理以及代码解析。
形式化LDA
上面对LDA进行了形象的描述以及相关的数学讨论,现在我们来更准确地,形式化地描述一下LDA。下图为LDA的概率图模型。

| 符号 | 解释 |
|---|---|
| M | 文章的数量 |
| K | 主题的个数 |
| V | 词袋的长度 |
| Nm | 第m篇文章中单词的总数 |
| 是每篇文章的主题分布的先验分布Dirichlet分布的参数(也被称为超参数)通常是手动设定的 | |
| 是每个主题的词分布的先验分布Dirichlet分布的参数(也被称为超参数)通常是手动设定的 | |
| θ是一个M*K的矩阵,表示第m篇文章的主题分布,是我们要求的参数 | |
| φ是一个K*V的矩阵,表示第k个主题的词分布,是我们要求的参数 | |
| 第m篇文章第n个词被赋予的主题,隐变量 | |
| 第m篇文章第n个词,这个是可以被我们观测到的 |
LDA模型文章的生成过程如下:
选择一个ϑ⃗ m∼Dir(α⃗ )
对每个准备生成的单词Wm,n
(a)选择一个主题Zm,n~Multinomial(ϑ⃗ m)
(b)生成一个单词Wm,n从P(Wm,n|Zm,n,β⃗ )
根据上节的讨论,可以推导出主题分布:

词分布有类似的形式。
这里参数转化为每个topic的单词计数以及词分布的单词计数。概率将有这些计数除它们对应的总数所得。