【数据挖掘】决策树归纳中ID3算法讲解及构建决策树实战（图文解释 超详细）_id3决策树

需要完整PPT请点赞关注收藏后评论区留言私信~~~

1：分类概述

分类是一种重要的数据分析形式。数据分类也称为监督学习，包括学习阶段（构建分类模型）和分类阶段（使用模型预测给定数据的类标号）两个阶段。数据分类方法主要有决策树归纳、贝叶斯分类、K-近邻分类、支持向量机SVM等方法

 2：决策树规约

决策树属于经典的十大数据挖掘算法之一，是一种类似于流程图的树型结构，其规则就是if…then…的思想，用于数值型因变量的预测和离散型因变量的分类。决策树算法简单直观，容易解释，而且在实际应用中具有其他算法难以比肩的速度优势

决策树方法在分类、预测和规则提取等领域有广泛应用。在20世纪70年代后期和80年代初期，机器学习研究人员J.Ross Quinlan开发了决策树算法，称为迭代的二分器（Iterative Dichotomiser, ID3），使得决策树在机器学习领域得到极大发展。Quinlan后来又提出ID3的后继C4.5算法，成为新的监督学习算法的性能比较基准。1984年几位统计学家又提出了CART分类算法

决策树的构建原理

决策树是树状结构，它的每个叶结点对应着一个分类，非叶结点对应着在某个属性上的划分，根据样本在该属性上的不同取值将其划分为若干子集。ID3、C4.5和CART算法都采用贪心（即非回溯）方法，以自顶向下递归的分治方式构造，随着树的构建，训练集递归地被划分为子集

决策树构造过程描述如下图

3：ID3算法

ID3算法是决策树系列中的经典算法之一，包含了决策树作为机器学习算法的主要思想。但ID3算法在实际应用中有诸多不足，因此之后提出了大量的改进算法，如C4.5算法和CART算法。构造决策树的核心问题是在每一步如何选择恰当的属性对样本做拆分。ID3算法使用信息增益作为属性选择度量，C4.5使用增益率进行属性选择度量，CART算法则使用基尼指数

信息增益

 

 Gain（A）表明通过A上的划分获得了多少信息增益。选择具有最高信息增益的属性A作为结点N的分裂属性，等价于在“能做最佳分类”的属性A上划分，可以使得完成元组分类还需要的信息最小

 下面我们实战利用信息增益构建决策树

 

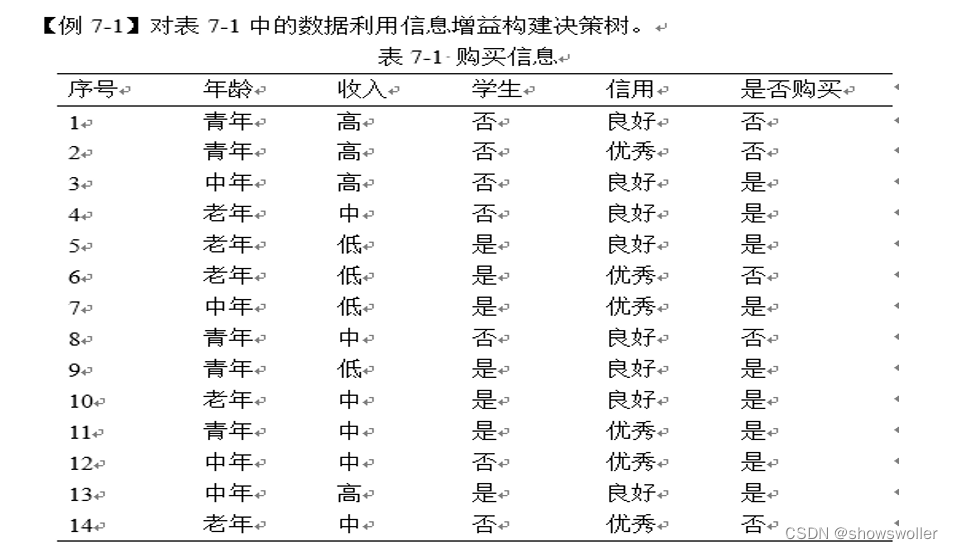
 紧接着，计算每个属性的期望信息需求。从属性年龄开始，需要对每个类考察“是”和“否”元组的分布。对于年龄的类“青年”，有5个取值，分别对应2个“是”和3个“否”，即为I(2, 3)，同理，类“中年”对应的是I(4, 0)，类“老年”对应的是I(3, 2)，因此，如果元组根据年龄划分，则对D中的元组进行分类所需要的期望信息为：

 

由于年龄在各属性中具有最高的信息增益，所以选用年龄作为分裂属性，节点N用年龄标记，并且每个属性值生长出一个分支 元组据此划分 如下图所示

 

 假设属性 A是连续的，必须确定A的最佳分裂点，其中分裂点是A上的阈值。首先，对属性A的取值排序。典型地，每对相邻值的中点被看作可能的分裂点，给定A的v个值，需要计算v-1个可能的划分。确定A的最佳分裂点只需扫描一遍这些值，对每个可能分裂点，分别计算其信息增益值，具有最大信息增益的分裂点即为最佳分裂值。自该分裂点把整个取值区间划分为两部分，相应的依据记录在该属性上的取值，也将记录划分为两部分

ID3算法的优缺点

ID3算法理论清晰，方法简单，学习能力较强。但也存在以下一些缺点

（1）信息增益的计算依赖于特征数目较多的特征，而属性取值最多的属性并不一定最优。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值比取2个值的信息增益大

（2）ID3没考虑连续特征，比如长度、密度都是连续值，无法在ID3运用

（3）ID3算法是单变量决策树（在分支结点上只考虑单个属性），许多复杂概念的表达困难，属性相互关系强调不够，容易导致决策树中子树的重复或有些属性在决策树的某一路径上被检验多次

（4）算法的抗噪性差，训练例子中正例和反例的比例较难控制，而且没有考虑缺失值和过拟合问题

创作不易 觉得有帮助请点赞关注收藏~~~