Fast planner 基本原理学习(一)

一、主题：Fast planner 基本原理学习

二、目标：

• 理解Fast planner轨迹规划处理流程
• 理解hybrid A*的改进点
• B样条曲线定义、性质、以及所带来的便利

三、正文：

1、Fast planner轨迹规划处理流程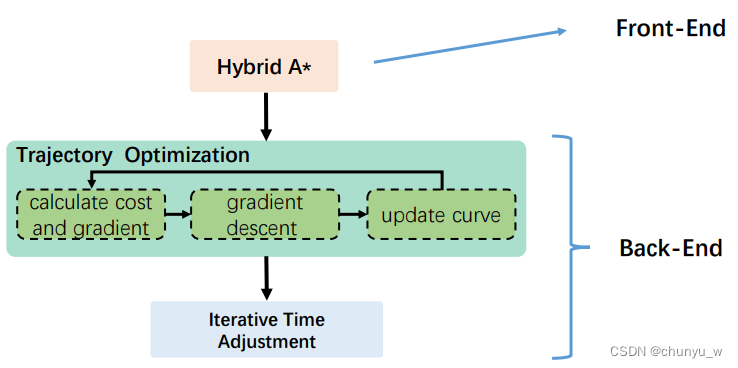

主要思想：前端考虑动力学进行规划，后端轨迹优化利用B样条曲线的性质。

• 前端考虑动力学的作用：1、为了后端优化能得到效果更好的轨迹。2、利用Forward direction:discrete (sample) in control space可以很好的几何到A*算法中。
• 后端采用B样条曲线作轨迹规划，在位置上，可以利用几个控制点描述一条曲线，利用B样条曲线的性质，可以将对轨迹的约束、动力学的约束加在控制点上，从而简化了计算。处理顺序是：1、先通过esdf地图提供梯度场信息，设计惩罚函数，使轨迹向障碍物少的地方移动。然后轨迹几何位置不变。在进行时间重分配，使轨迹符合动力学约束（最大速度、最大加速度在允许范围内。）
• 备注：运动规划的轨迹是一条带时间参数的轨迹，同时需要符合避障、动力学的约束。一般工程上前端用来完成满足避障的几何路线。动力学的优化一般放在后端。

优点：
1、使轨迹向梯度场小的方向移动，设计出来的轨迹在障碍物中间，相较其他方法会更加安全。
2、利用了B样条曲线，带来了很大的便利，因为B样条曲线具有以下性质:

•   改变任意控制点，只改变有限时间段的轨迹。
  1

•   Ｂ样条曲线的导数仍为Ｂ曲线。
  1

缺点：

2、前端处理流程

3、Ｂ样条曲线

贝塞尔曲线（Bezier Curve）

1. 定义
   $$\mathbf{B}(t)=\sum _{i=0}^{n-1}{R}_{i,n}(t){\mathbf{P}}_i{R}_{i,n}(t)=C_n^i{t}^i(1-t{)}^{n-i}t\in [0,1]$$
2. 性质

• 曲线的阶数随着控制点的增加而增加。
• 改变任意一点会影响到整段轨迹。

---

B样条曲线（Ｂ-Spline)

1. 定义
   $$\mathbf{C}(t)=\sum _{i=0}^n{N}_{i,p}(t){\mathbf{Q}}_i$$
   

2. 性质

• 更改控制点(control point)只能影响有限的时间，如图，如果 $Q_3$ 的点发生移动。只有在时间段u1～u5内，$N_{1,3}$不为0。所以改变Q3的位置影响的时间段是有限的。
  

时间范围为什么两边缩小Pb的偏移，由下图可以很容易看出来。

• 一个时间段的轨迹由有限的点决定
  如图，$[u_3,u_4)$的时间段只受到$Q_0、Q_1、Q_2、Q_3$控制点的作用。
  

• p>=1具有轨迹连续性质
  推到出C(t)的表达式易证。

• B样条的导数还是B样条

  • 1阶导
    $$\mathbf{C}\dot{(}u)=\sum _{i=0}^{n-1}{N}_{i+1,p-1}(u){\mathbf{V}}_i$$
  • 2阶导
    $$\mathbf{C}\ddot{(}u)=\sum _{i=0}^{n-2}{N}_{i+2,p-2}(u){\mathbf{A}}_i$$
  • 控制点的计算
    $${\mathbf{V}}_i=\frac{p\left({\mathbf{Q}}_{i+1}-{\mathbf{Q}}_i\right)}{u_{i+p+1}-u_{i+1}}$$
    $${\mathbf{A}}_i=\frac{(p-1)\left({\mathbf{V}}_{i+1}-{\mathbf{V}}_i\right)}{u_{i+p+1}-u_{i+2}}$$
  • 通过对高阶的轨迹表达式求导，可得到物理含义的速度、加速度等信息，且可是B样条曲线，方便利用B样条曲线的凸包性质。

• 凸包性质（Convex Hull Property）

  • 直观上看，如下图，最左边的橙色时间段段为控制点$Q_{0}、Q_{1}、Q_{2}、Q_{3}$控制，可见这段轨迹是在控制点的连线区域内的。时间段以此类推，都在其对应控制点连线的多边行区域内。因此容易将轨迹的障碍物的距离约束，速度、加速度约束，转化到对控制点的约束，从而简化计算。
    

• 时间均匀的B样条可以化成特殊的表达形式（Fast Planner中使用
  通式：
  

  当p = 3， m = 3:
  p ( s ( u ) ) = s ( u ) T M 4 q 3 s ( u ) = [ 1 s ( u ) s 2 ( u ) s 3 ( u ) ] T q 3 = [ Q 0 Q 1 Q 2 Q 3 ] T s ( u ) = ( u − u 3 ) / Δ u

  $$\begin{aligned} \mathbf{p}(s(u)) &=\mathbf{s}(u)^{\mathrm{T}} \mathbf{M}_{4} \mathbf{q}_{3} \\ \mathbf{s}(u) &=\left[\begin{array}{llll} 1 & s(u) & s^{2}(u) & s^{3}(u) \end{array}\right]^{\mathrm{T}} \\ \mathbf{q}_{3} &=\left[\begin{array}{llll} \mathbf{Q}_{0} & \mathbf{Q}_{1} & \mathbf{Q}_{2} & \mathbf{Q}_{3} \end{array}\right]^{\mathrm{T}} \\ s(u) &=\left(u-u_{3}\right) / \Delta u \end{aligned}$$ p(s(u))s(u)q3​s(u)​=s(u)TM4​q3​=[1​s(u)​s2(u)​s3(u)​]T=[Q0​​Q1​​Q2​​Q3​​]T=(u−u3​)/Δu​
  推导：

  

N 0 , 3 ( t ) = 1 6 { t 3 t ∈ [ 0 , 1 ) t 2 ( 2 − t ) + t ( 3 − t ) ( t − 1 ) + ( 4 − t ) ( t − 1 ) 2 t ∈ [ 1 , 2 ) t ( 3 − t ) 2 + ( t − 1 ) ( 3 − t ) ( 4 − t ) + ( 4 − t ) 2 ( t − 2 ) t ∈ [ 2 , 3 ) ( 4 − t ) 3 t ∈ [ 3 , 4 ) N_{0,3}(t)=\frac{1}{6}\left\{

$$\begin{array}{cl} t^{3} & t \in[0,1) \\ t^{2}(2-t)+t(3-t)(t-1)+(4-t)(t-1)^{2} & t \in[1,2) \\ t(3-t)^{2}+(t-1)(3-t)(4-t)+(4-t)^{2}(t-2) & t \in[2,3) \\ (4-t)^{3} & t \in[3,4) \end{array}$$ \right. N0,3​(t)=61​⎩⎪⎪⎨⎪⎪⎧​t3t2(2−t)+t(3−t)(t−1)+(4−t)(t−1)2t(3−t)2+(t−1)(3−t)(4−t)+(4−t)2(t−2)(4−t)3​t∈[0,1)t∈[1,2)t∈[2,3)t∈[3,4)​
$$\begin{gathered} N_{1,3}(t)=\frac{1}{6}\{\begin{array}{cl}(t-1{）}^3& t\in [1,2)\\ （t-1{）}^2(1-t)+（t-1）(2-t)(t-2)+(3-t)(t-2{)}^2& t\in [2,3)\\ （t-1）(2-t{)}^2+(t-2)(2-t)(3-t)+(3-t{)}^2(t-3)& t\in [3,4)\\ (3-t{)}^3& t\in [4,5)\end{array} \\ ... \end{gathered}$$
可计算$t\in [u_3,u_4)$段的轨迹：
推广到$t\in [u_m,u_{m+1})$段的轨迹：
结论：由公式看出，只需要$Q_{m-3}、Q_{m-2}、Q_{m-1}、Q_m$的点，分配时间$\Delta u$，就可以确定`$t\in [u_m,u_{m+1})$段轨迹。

p ( s ( u ) ) = s ( u ) T M 4 q m s ( u ) = [ 1 s ( u ) s 2 ( u ) s 3 ( u ) ] T q m = [ Q m − 3 Q m − 2 Q m − 1 Q m ] T s ( u ) = ( u − u m ) / Δ u

$$\begin{aligned} \mathbf{p}(s(u)) &=\mathbf{s}(u)^{\mathrm{T}} \mathbf{M}_{4} \mathbf{q}_{m} \\ \mathbf{s}(u) &=\left[\begin{array}{llll} 1 & s(u) & s^{2}(u) & s^{3}(u) \end{array}\right]^{\mathrm{T}} \\ \mathbf{q}_{m} &=\left[\begin{array}{llll} \mathbf{Q}_{m-3} & \mathbf{Q}_{m-2} & \mathbf{Q}_{m-1} & \mathbf{Q}_{\mathrm{m}} \end{array}\right]^{\mathrm{T}} \\ s(u) &=\left(\begin{array}{llll} \left.u-u_{m}\right) / \Delta u \end{array}\right.\\ \end{aligned}$$ p(s(u))s(u)qm​s(u)​=s(u)TM4​qm​=[1​s(u)​s2(u)​s3(u)​]T=[Qm−3​​Qm−2​​Qm−1​​Qm​​]T=(u−um​)/Δu​​
$${\mathbf{M}}_4=\frac{1}{3!}\left[\begin{array}{cccc}1& 4& 0& 0\\ -3& 0& 3& 0\\ 3& -6& 3& 0\\ -1& 3& -3& 1\end{array}\right]$$

---

3. 理解：B样条曲线是贝塞尔曲线的一种特殊情况，规定了基函数的形式，使B样条有一些新的性质。由三个重要元素组成： degree（阶数）、control points（控制点）、knot vector（时间向量）。

---

4. 基函数计算
   $$\begin{array}{l}{N}_{i,0}(u)=\{\begin{array}{lc}1& \text{ if }{u}_i\le u<u_{i+1}\\ 0& \text{ otherwise }\end{array}\\ N_{i,p}(u)=\frac{u-u_i}{u_{i+p}-u_i}{N}_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}{N}_{i+1,p-1}(u)\end{array}u代表时间变量$$

• 不同阶的基函数间的计算关系
  

• 0阶
  

• 1阶
  

• 2阶
  

可以看出： 0阶时轨迹就是控制点。1阶时控制点连线的直线。2阶导时控制点有光滑曲线连接（轨迹连续可导）。

• 注意：Faster Planner选用了三阶基函数。通过各阶基函数的计算关系，很好推导B样条曲线的性质。

4、后端处理流程

1. 代价函数的设计

   • smoothness cost $f_s$
     $$f_s=\sum _{i=p_b-1}^{N-p_b+1}{\Vert \left({\mathbf{Q}}_{i+1}-{\mathbf{Q}}_i\right)+\left({\mathbf{Q}}_{i-1}-{\mathbf{Q}}_i\right)\Vert }^2$$
     

   2. dynamic feasibility cost $f_v+f_a$
      设计惩罚函数
      
      

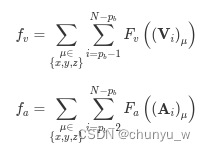
      注意：因为是软约束，所以后续需要进行时间调整

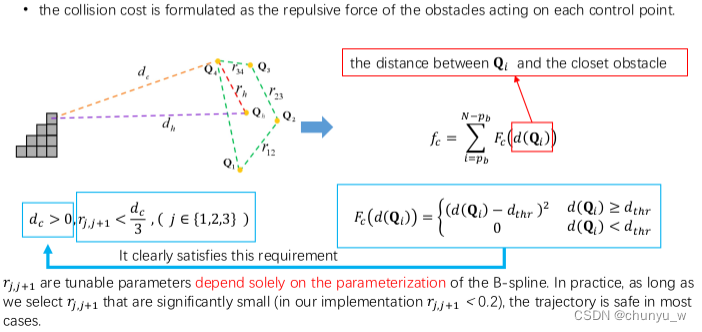
   3. collision cos $f_c$

      $$f_c=\sum _{i=p_b}^{N-p_b}{F}_c\left(d\left({\mathbf{Q}}_i\right)\right)$$
      可见，由B样条曲线的凸包性质，轨迹的约束都可以转化到控制点上，简化了计算。
      

2. 时间调整

参考：

《深蓝学院》移动机器人运动规划第8章