繁依Fanyi0

这个屌丝很懒，什么也没留下！

热门标签

《数据结构》：中缀表达式转后缀表达式 + 后缀表达式的计算

作者：繁依Fanyi0 | 2024-04-27 04:48:45

踩

中缀表达式转后缀表达式

补充了一个判断输入中缀表达式合法性的代码：

《数据结构》：中缀表达式合法性判断_Amentos的博客-CSDN博客

一、基本概念

二、中缀表达式转后缀表达式

例中缀表达式 2*(3+5)+7/1-4 转换为后缀表达式

三、后缀表达式的计算

例后缀表达式 2 3 5 + * 7 1 / + 4 - 的计算

四、算法实现

五、算法改进

一、基本概念

1、中缀表达式：

操作符以中缀形式位于运算数中间（如：3+2），是我们日常通用的算术和逻辑公式表示方法。

2、后缀表达式：

又称逆波兰式（Reverse Polish Notation - RPN），操作符以后缀形式位于两个运算数后（如：3+2的后缀表达形式就是3 2 +）。

3、前缀表达式：

又称波兰式（Polish Notation），操作符以前缀形式位于两个运算数前（如：3+2的前缀表达形式就是+ 3 2）。

中缀表达式往往需要使用括号将操作符和对应的操作数括起来，用于指示运算的次序

e.g：5*(2+1) 虽然 * 的优先级高于 + ，但括号的存在表示应优先执行括号内的 + 运算。

中缀表达式适合于人类的思维结构和运算习惯，但并不适用于计算机

尤其是包含括号的中缀表达式，对计算机而言是非常复杂的结构。

适用于计算机的后缀表达式

与中缀表达式不同，后缀表达式不需要使用括号来标识操作符的优先级。

后缀表达式的计算按 操作符 从左到右出现的顺序依次执行(不考虑运算符之间的优先级)，对于计算机而言是比较简单的结构。

二、中缀表达式转后缀表达式

从左至右依次遍历中缀表达式各个字符（需要准备一个字符栈存储操作符和括号）

1、字符为 运算数 ：

直接送入后缀表达式（注：需要先分析出完整的运算数）。

2、字符为 左括号 ：

直接入栈（注：左括号入栈后优先级降至最低）。

3、字符为 右括号 ：

直接出栈，并将出栈字符依次送入后缀表达式，直到栈顶字符为左括号（左括号也要出栈，但不送入后缀表达式）。

总结：只要满足栈顶为左括号即可进行最后一次出栈。

4、字符为 操作符 ：

若栈空，直接入栈。

若栈非空，判断栈顶操作符，若栈顶操作符优先级低于该操作符，该操作符入栈；否则一直出栈，并将出栈字符依次送入后缀表达式，直到栈空或栈顶操作符优先级低于该操作符，该操作符再入栈。

总结：只要满足栈空或者优先级高于栈顶操作符即可停止出栈，并将该操作符入栈。

5、重复以上步骤直至遍历完成中缀表达式，接着判断字符栈是否为空，非空则直接出栈，并将出栈字符依次送入后缀表达式。

注：中缀表达式遍历完成，栈中可能还有字符未输出，故需要判断栈空。

**例中缀表达式 2*(3+5)+7/1-4 转换为后缀表达式**

从左至右依次遍历中缀表达式各个字符：

第一个字符为运算数，直接输出：

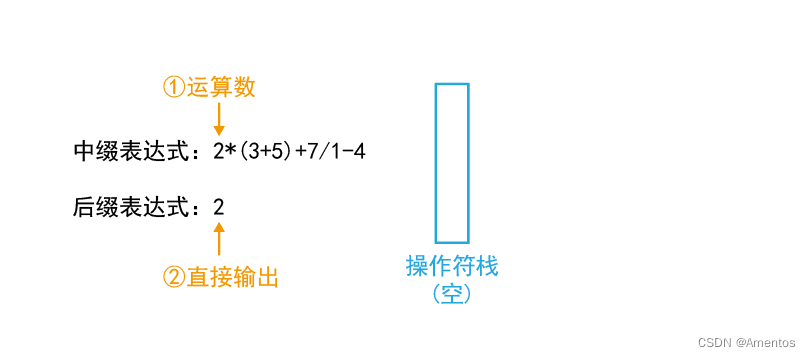
第二个字符为操作符，满足栈空/优先级高于栈顶操作符条件，该操作符入栈：

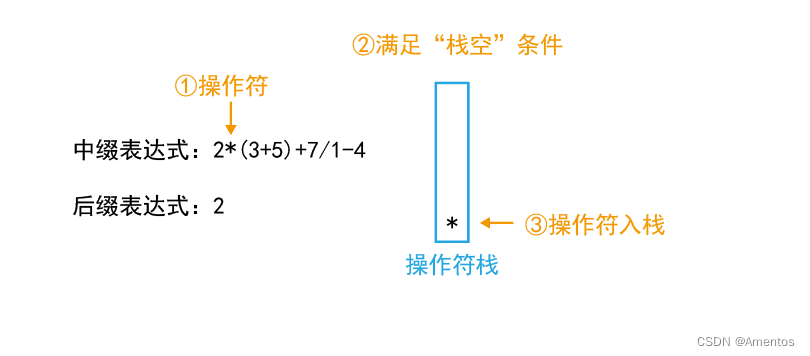
第三个字符为左括号，直接入栈（入栈后优先级降至最低）：

第四个字符为运算数，直接输出：

第五个字符为操作符，满足栈空/优先级高于栈顶操作符 条件，该操作符入栈：

第六个字符为运算数，直接输出：

第七个字符为右括号，直接出栈并输出，直到栈顶为左括号时进行最后一次出栈(不输出)：

第八个字符为操作符，不满足栈空/优先级高于栈顶操作符条件，出栈直至满足条件

第九个字符为运算数，直接输出：

第十个字符为操作符，满足栈空/优先级高于栈顶操作符 条件，该操作符入栈：

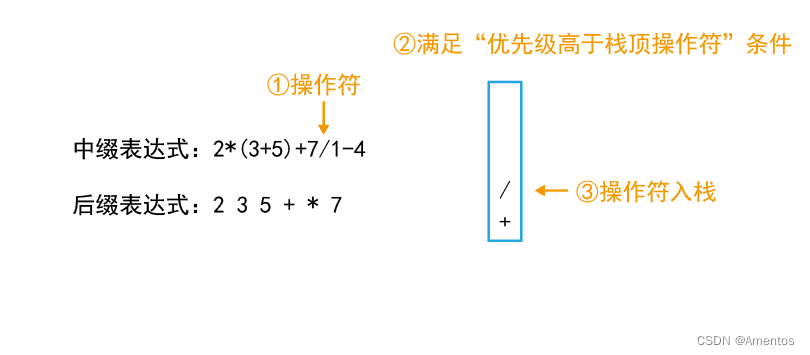
第十一个字符为运算数，直接输出：

第十二个字符为操作符，不满足栈空/优先级高于栈顶操作符条件，出栈直至满足条件：

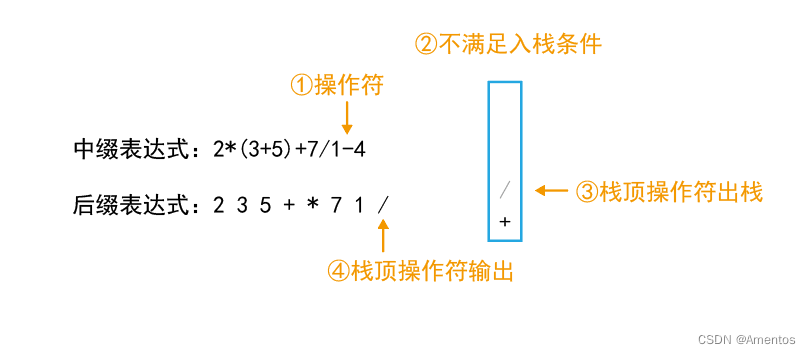
第十三个字符为运算数，直接输出：

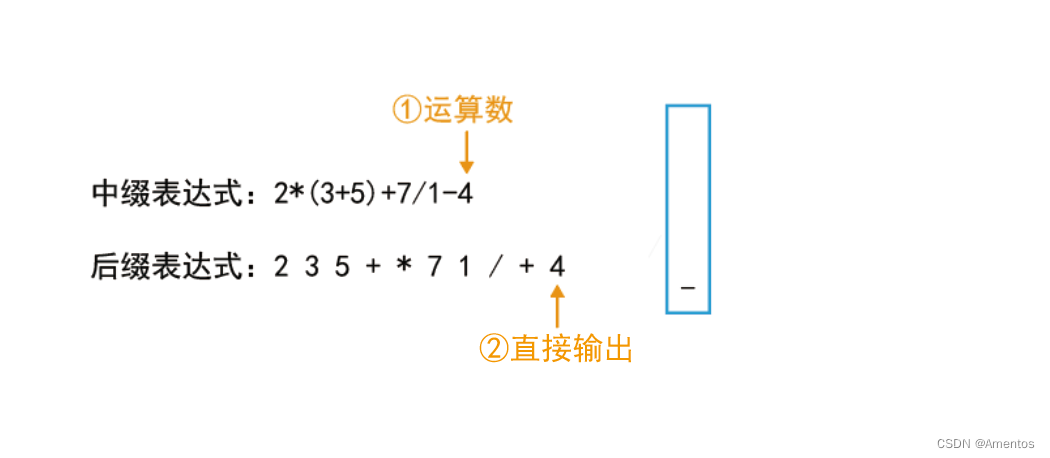
中缀表达式遍历完成，判断字符栈中是否还有操作符，如有则出栈并输出：

转换完成：

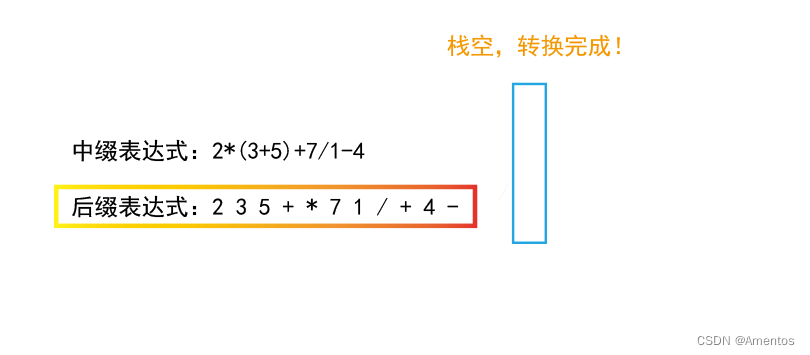
三、后缀表达式的计算

从左至右依次遍历后缀表达式各个字符（需要准备一个运算数栈存储运算数和操作结果）

1、字符为 运算数 ：

直接入栈（注：需要先分析出完整的运算数并将其转换为对应的数据类型）

2、字符为 操作符 ：

连续出栈两次，使用出栈的两个数据进行相应计算，并将计算结果入栈

e.g：第一个出栈的运算数为 a ，第二个出栈的运算数为 b ，此时的操作符为 - ，则计算 b-a （注：a和b顺序不能反），并将结果入栈。

3、重复以上步骤直至遍历完成后缀表达式，最后栈中的数据就是中缀表达式的计算结果。

例后缀表达式 **2 3 5 + * 7 1 / + 4 -** 的计算

从左至右依次遍历后缀表达式各个字符：

第一个字符为运算数，直接入栈：

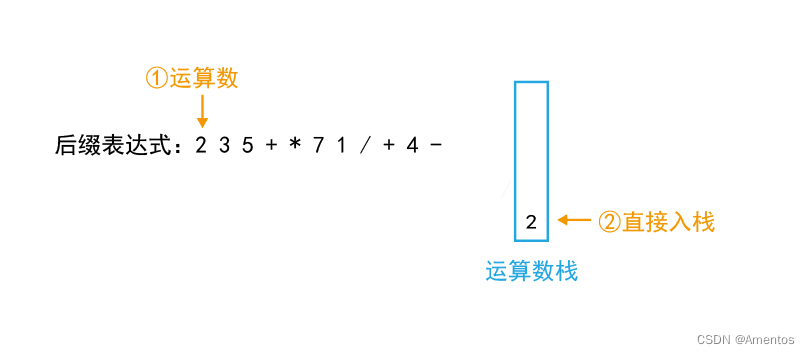
第二个字符为运算数，直接入栈：

第三个字符为运算数，直接入栈：

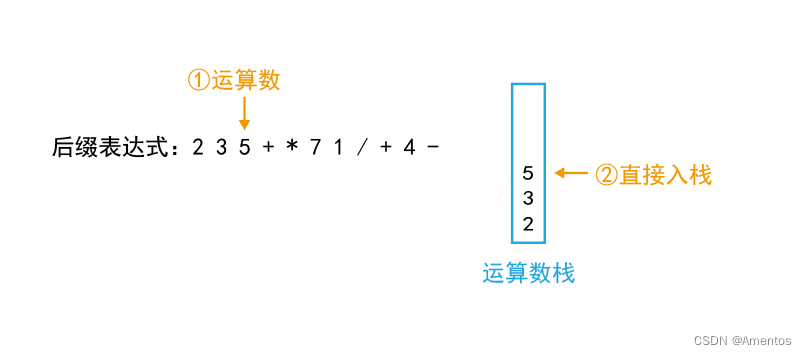
第四个字符为操作符，直接出栈两次：

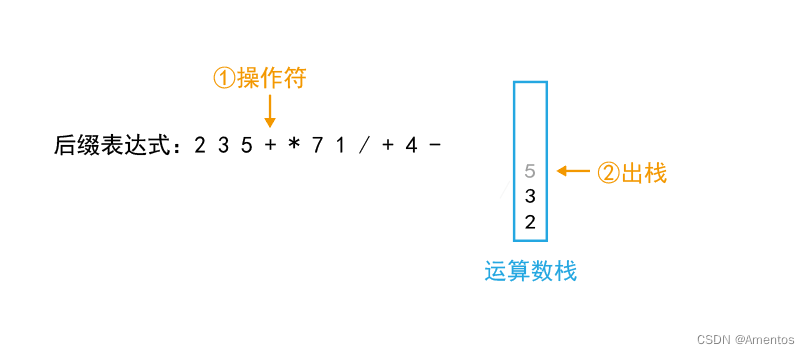
继续出栈：

执行：第二次出栈运算数操作符第一次出栈运算数

即：3 + 5

结果：8

将计算结果入栈：

第五个字符为操作符，直接出栈两次：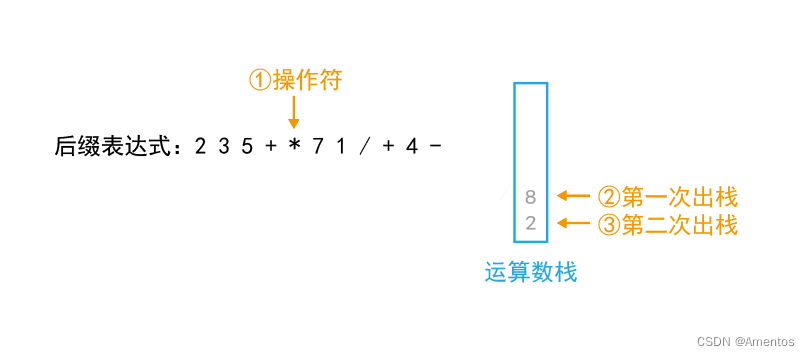

执行：第二次出栈运算数操作符第一次出栈运算数

即：2 * 8

结果：16

将计算结果入栈：

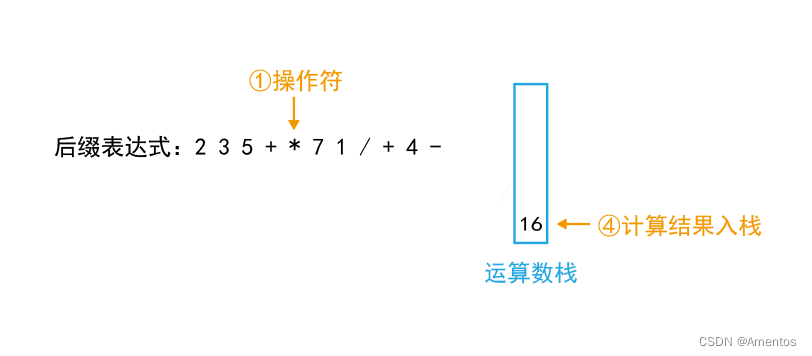
第六个字符为运算数，直接入栈：

第七个字符为运算数，直接入栈：

第八个字符为操作符，直接出栈两次：

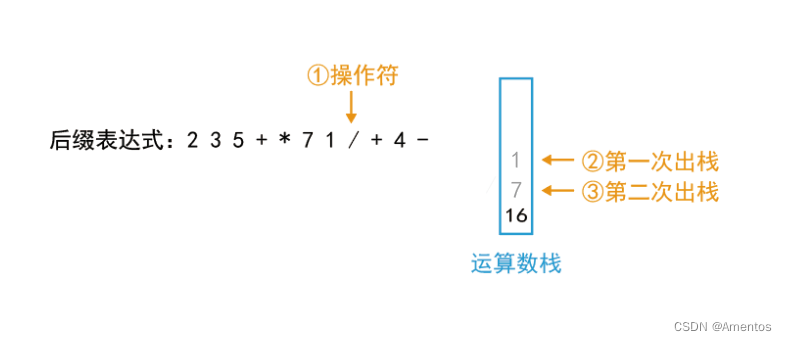
执行：第二次出栈运算数操作符第一次出栈运算数

即：7 / 1

结果：7

将计算结果入栈：

第九个字符为操作符，直接出栈两次：

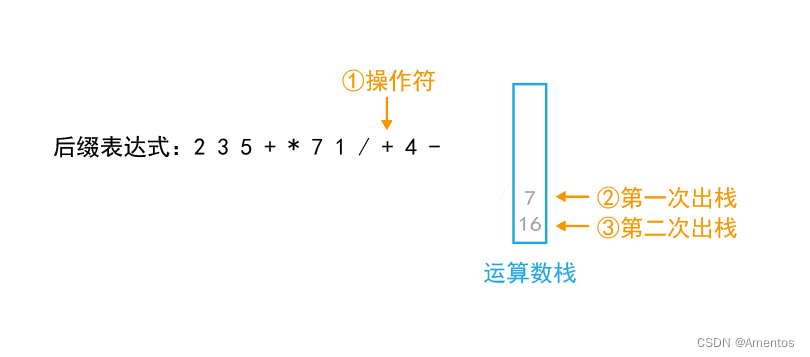
执行：第二次出栈运算数操作符第一次出栈运算数

即：16 + 7

结果：23

将计算结果入栈：

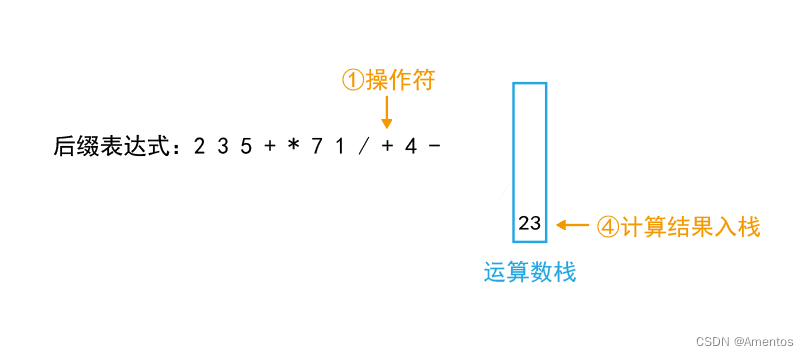
第十个字符为运算数，直接入栈：

第十一个字符为操作符，直接出栈两次：

执行：第二次出栈运算数操作符第一次出栈运算数

即：23 - 4

结果：19

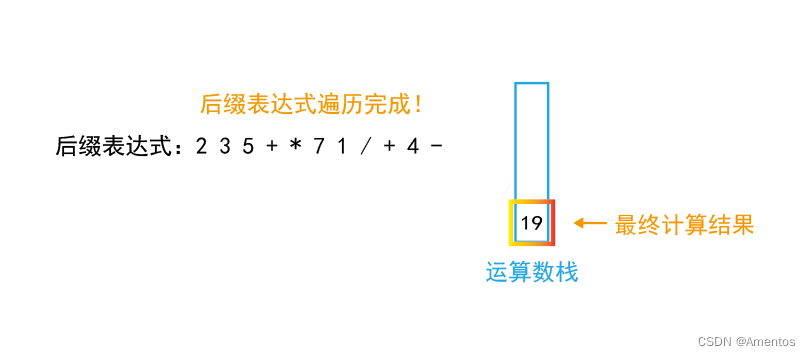
将计算结果入栈：

后缀表达式遍历完成，栈中数据即为最终计算结果：

四、算法实现

程序代码：


#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#include<ctype.h>
 
#define ERROR 0
#define OK 1
#define STACK_INT_SIZE 10  /*存储空间初始分配量*/
#define STACKINCREMENT 5  /*存储空间分配增量*/
#define M 50
 
typedef char ElemType; /*定义字符数据类型*/
typedef double ElemType2;  /*定义运算数数据类型*/
 
/*字符栈*/
typedef struct{
    ElemType *base;
    ElemType *top;
    int stacksize; 
}SqStack;
 
/*运算数栈*/
typedef struct{
    ElemType2 *base;
    ElemType2 *top;
    int stacksize;
}NStack;
 
int InitStack(SqStack *S);   /*构造空栈*/
int push(SqStack *S,ElemType e); /*入栈*/
int Pop(SqStack *S,ElemType *e);  /*出栈*/
int StackEmpty(SqStack *s);  /*栈空判断*/
void in2post(ElemType *str,ElemType *p);  /*中缀表达式转后缀表达式*/
double cal_post(char *str);  /*计算后缀表达式*/
 
/*字符栈初始化*/
int InitStack(SqStack *S){
    S->base=(ElemType *)malloc(STACK_INT_SIZE * sizeof(ElemType));
    if(!S->base)
        return ERROR;  //分配失败
    S->top = S->base;
    S->stacksize = STACK_INT_SIZE;
    return OK;
}/*InitStack*/
 
/*运算数栈初始化*/
int InitStack_N(NStack *S){
    S->base=(ElemType2 *)malloc(STACK_INT_SIZE * sizeof(ElemType2));
    if(!S->base)
        return ERROR;
    S->top = S->base;
    S->stacksize = STACK_INT_SIZE;
    return OK;
}
 
/*字符栈入栈*/
int Push(SqStack *S,ElemType e){
    //判断栈满
    if(S->top - S->base >= S->stacksize){
        S->base = (ElemType *)realloc(S->base,(S->stacksize + STACKINCREMENT)*sizeof(ElemType));
        if(NULL == S->base)  //分配失败
            return ERROR;
        S->top = S->base + S->stacksize;
        S->stacksize = S->stacksize+STACKINCREMENT;
    }
    *S->top = e;
    S->top++;
    return OK;
}
 
/*运算数栈入栈*/
int Push_N(NStack *S,ElemType2 e){
    if(S->top - S->base >= S->stacksize){
        S->base = (ElemType2 *)realloc(S->base,(S->stacksize + STACKINCREMENT)*sizeof(ElemType2));
        if(NULL == S->base)
            return ERROR;
        S->top = S->base + S->stacksize;
        S->stacksize = S->stacksize+STACKINCREMENT;
    }
    *S->top = e;
    S->top++;
    return OK;
}
 
/*字符栈出栈*/
int Pop(SqStack *S,ElemType *e){
    //判断栈空
    if(S->top == S->base)
        return ERROR;
    S->top--;
    *e=*S->top;
    return OK;
}/*Pop*/
 
/*运算数栈出栈*/
int Pop_N(NStack *S,ElemType2 *e){
    if(S->top == S->base)
        return ERROR;
    S->top--;
    *e=*S->top;
    return OK;
}
 
/*判断栈空*/
int StackEmpty(SqStack *s){
    if(s->top == s->base)
        return OK;
    return ERROR;
}/*StackEmpty*/
 
//str为待转换的中缀表达式字符串,p为转换后的后缀表达式字符串
void in2post(ElemType *str,ElemType *p){   /*infix to postfix*/
    SqStack s;   
    InitStack(&s);   //初始化一个空字符栈
    ElemType e;
    int i;
    int j=0;
    for(i=0 ; i<strlen(str) ; i++)  //遍历中缀表达式
    {
        //遇到数字和小数点直接输出
        //使用循环完整接收一个运算数
        while(isdigit(str[i]) || '.'==str[i])
        {
            p[j++]=str[i++];
            if(!isdigit(str[i]) && '.'!=str[i])
                p[j++]=' ';   //一个数字完整输出后使用空格与其它运算符或数字分隔开
        }
 
        //遇到左括号直接入栈
        if('('==str[i])
            Push(&s,str[i]);
 
        //遇到右括号直接出栈，直到栈顶为左括号
        if(')'==str[i])
        {
            while('(' != *(s.top-1))
            {
                Pop(&s,&e);
                p[j++]=e;
                p[j++]=' ';
            }
            Pop(&s,&e);  //左括号出栈但不输出
        }
 
        //遇到+或—
        //1.栈空/栈顶为左括号:直接入栈
        //2.否则一直出栈,直到栈空/栈顶为左括号,再入栈
        if('+'==str[i] || '-'==str[i])
        {
            while(!StackEmpty(&s) && '('!=*(s.top-1))
            {
                Pop(&s,&e);
                p[j++]=e;
                p[j++]=' ';
            }
            Push(&s,str[i]);
        }
 
        //遇到*或/
        //1.栈空/栈顶为左括号/栈顶操作符为+ or -:直接入栈
        //2.否则一直出栈,直到满足1,再入栈
        if('*'==str[i] || '/'==str[i] || '%'==str[i])
        {
            while(!StackEmpty(&s) && '('!=*(s.top-1) && '+'!=*(s.top-1) && '-'!=*(s.top-1))
            {
                Pop(&s,&e);
                p[j++]=e;
                p[j++]=' ';
            }
            Push(&s,str[i]);
        }
    }
    //中缀表达式遍历完成,还需检查栈中是否有未输出字符
    //判断栈空,非空则直接出栈并输出(左括号不用输出)
    while(!StackEmpty(&s)){
        Pop(&s,&e);
        if('('!=e)
        {
            p[j++]=e;
            p[j++]=' ';
        }
    }
    p[--j]='\0';
}/*infix2postfix*/
 
//str为待计算的后缀表达式,返回值为计算结果
double cal_post(char *str){   /*计算后缀表达式*/
    int i;
    ElemType2 e,a,b;
    char d[M];
    NStack n;
    InitStack_N(&n);   //初始化一个运算数栈保存运算数
    for(i=0;i<strlen(str);i++)
    {
        int j=0;
        while(isdigit(str[i]) || '.'==str[i])
        {
            d[j++]=str[i++];
            d[j]='\0';
            if(!isdigit(str[i]) && '.'!=str[i])
            {
                e=atof(d);   //使用atof()将字符串形式的运算数转换为double型数据
                Push_N(&n,e);   //运算数入栈
            }
        }
        switch(str[i])
        {
            case '+':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a+b);
                break;
            case '-':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a-b);
                break;
            case '*':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a*b);
                break;
            case '/':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a/b);
                break;
        }
    }
    Pop_N(&n,&e);
    return e;
}/*calculate_postfix*/
 
int main()
{
    char str[M];
    char post[M];
    int i;
    printf("\n输入一串中缀表达式：\n");
    gets(str);
    printf("\n对应的后缀表达式：\n");
    in2post(str,post);
    printf("%s",post);
    printf("\n\n计算后缀表达式：\n");
    printf("%f",cal_post(post));
    return 0;
}

运行结果：

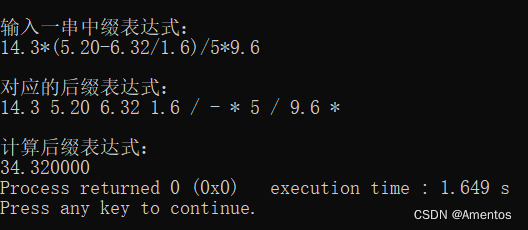
五、算法改进

上面的代码正确运算的前提是：

① 输入的中缀表达式合法

② 运算数非负数

例如：输入 3*(-6+5) ，得到以下结果，后缀表达式和运算结果明显不正确。

这里的 -6 应该才是一个完整的运算数，但是在后缀表达式中 '-' 号和数字 '6' 被拆分开来了，得到的结果也不正确。因为代码中对于 '-' 号一律是作为操作符处理，所以面对像 -6 这样的负数时不能分析出完整正确的运算数。

如果要进行修改，在进行运算数分析的时候就要考虑负数的情况。当出现 '-' 号的时候，要判断它是作为负数标志，属于运算数的一部分，还是作为一个运算符。

所以需要对运算数分析的代码添加负数的处理，修改后的代码如下：

in2post 函数代码修改：


void in2post(ElemType *str,ElemType *p){   /*infix to postfix*/
    //初始化一个空栈
    SqStack s;
    InitStack(&s);
    ElemType e;
 
    int i;
    int j=0;
    for(i=0 ; i<strlen(str) ; i++)  //遍历中缀表达式
    {
        if('-' == str[i])    //负数情况判断
        {
            //表达式首位是'-',则一定是作为负数符号
            if(0 == i)
                p[j++]=str[i++];
            //'-'前面是'(',则一定是作为负数符号
            else if('(' == str[i-1])
                p[j++]=str[i++];
        }
 
 
        //遇到数字和小数点直接输出
        while(isdigit(str[i]) || '.'==str[i])
        {
            p[j++]=str[i++];
            if(!isdigit(str[i]) && '.'!=str[i])
                p[j++]=' ';   //一个数字完整输出后使用空格与其它运算符或数字分隔开
        }
 
        //遇到左括号直接入栈
        if('('==str[i])
            Push(&s,str[i]);
 
        //遇到右括号直接出栈，直到左括号出栈(左括号不输出)
        if(')'==str[i])
        {
            while('(' != *(s.top-1))
            {
                Pop(&s,&e);
                p[j++]=e;
                p[j++]=' ';
            }
            Pop(&s,&e);  //左括号出栈但不输出
        }
 
        //遇到+或—
        //1.栈空/栈顶为左括号:直接入栈
        //2.否则一直出栈,直到栈空/栈顶为左括号,再入栈
        if('+'==str[i] || '-'==str[i])
        {
            while(!StackEmpty(&s) && '('!=*(s.top-1))  //栈非空 且 栈顶非左括号
            {
                Pop(&s,&e);
                p[j++]=e;
                p[j++]=' ';
            }
            Push(&s,str[i]);
        }
 
        //遇到*或/
        //1.栈空/栈顶为左括号/栈顶操作符为+ or -:直接入栈
        //2.否则一直出栈,直到满足1,再入栈
        if('*'==str[i] || '/'==str[i] || '%'==str[i])
        {
            while(!StackEmpty(&s) && '('!=*(s.top-1) && '+'!=*(s.top-1) && '-'!=*(s.top-1))
            {
                Pop(&s,&e);
                p[j++]=e;
                p[j++]=' ';
            }
            Push(&s,str[i]);
        }
    }
    //中缀表达式遍历完成,还需检查栈中是否有未输出字符
    //判断栈空,非空则直接出栈并输出(左括号不用输出)
    while(!StackEmpty(&s)){
        Pop(&s,&e);
        if('('!=e)
        {
            p[j++]=e;
            p[j++]=' ';
        }
    }
    p[--j]='\0';
}

cal_post 函数代码修改：


double cal_post(char *str){
    ElemType2 e,a,b;
    char d[M];
    //初始化一个运算数栈保存运算数
    NStack n;
    InitStack_N(&n);
    int i=0;
    int j=0;
    while(str[i])  //遍历后缀表达式
    {
        switch(str[i])
        {
            case '-':
                if( isdigit(str[i+1]) )  //判断'-'是作为负数符号or运算符
                {
                    d[j++]=str[i++];  //将负号加入运算数字符串
                    d[j]='\0';
                    break;  //注:这里的break只是跳出switch循环
                }
                else
                {
                    Pop_N(&n,&b);
                    Pop_N(&n,&a);
                    Push_N(&n,a-b);
                    i++;
                    break;
                }
            case '+':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a+b);
                i++;
                break;
            case '*':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a*b);
                i++;
                break;
            case '/':
                Pop_N(&n,&b);
                Pop_N(&n,&a);
                Push_N(&n,a/b);
                i++;
                break;
            case ' ':i++;
        }
 
        //遇到运算数直接入栈(先转换double类型)
        //d保存后缀表达式中的字符串形式的运算数
        //使用atof将字符串转换为double类型
        while(isdigit(str[i]) || '.'==str[i])
        {
            d[j++]=str[i++];
            d[j]='\0';
            if( ' ' == str[i] )
            {
                e = atof(d);  //此时分析出的就是完整的运算数
                Push_N(&n,e);
                i++;
                j = 0;
            }
        }
    }
    Pop_N(&n,&e);
    return e;
}

运行结果：

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/494872

《数据结构》：中缀表达式转后缀表达式 + 后缀表达式的计算

一、基本概念

二、中缀表达式转后缀表达式

例 中缀表达式 2*(3+5)+7/1-4 转换为后缀表达式

三、后缀表达式的计算

例 后缀表达式 2 3 5 + * 7 1 / + 4 - 的计算

四、算法实现

五、算法改进

**例中缀表达式 2*(3+5)+7/1-4 转换为后缀表达式**

例后缀表达式 **2 3 5 + * 7 1 / + 4 -** 的计算