为什么-关于因果关系的新科学 | 01 因果关系之梯_为什么 因果关系的新科学

Reference[原文]: Joselynzhao.top & 夏木青 | 01 因果关系之梯

上帝问的是“什么”,他们回答的却是“为什么”。上帝询问事实,他们回答理由。
而且,两人都深信,列举原因可以以某种方式美化他们的行为。他们是从哪里得到这样的想法的?

人类祖先想象不存在之物的能力是一切的关键,正是这种能力让他们得以交流得更加顺畅。在获得这种能力之前,他们只相信自己的直系亲属或者本部落的人。而此后,信任就因共同的幻想
(例如信仰无形但可想象的神,信仰来世,或者信仰领袖的神性)和期许而延伸到了更大的群体。

回到我们的智人祖先,新掌握的因果想象力使他们能够通过一种被我们称为“规划”的复杂过程更有效地完成许多事情。

简言之,通过想象和比较几个狩猎策略的结果来完成任务。要做到这一点,
思维主体必须具备一个可供参考并且可以自主调整的关于狩猎现实的心理模型.

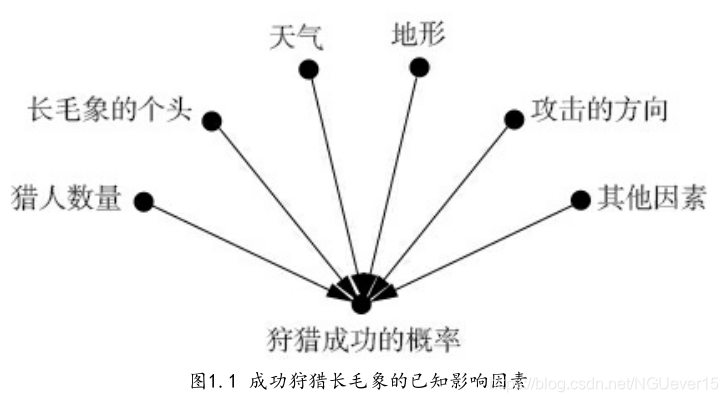
图1.1展示了我们建构这一心理模型的方式。图中的每个点都代表一种成功狩猎的影响因素或原因。

心理模型是施展想象的舞台。 它使我们能够通过对模型局部的修改来试验不同的情景。
这些因果图就是我在导言中所描述的“因果推理引擎”的计算核心。

因果关系的三个层级

因果关系的学习者必须熟练掌握至少三种不同层级的认知能力:观察能力(seeing)、行动能力
(doing)和想象能力(imagining)。

第一层级是观察能力,具体而言是指发现环境中的规律的能力。
第二层级是行动能力,涉及预测对环境进行刻意改变后的结果,并根据预测结
果选择行为方案以催生出自己期待的结果。对工具的使用(前提是使用是有意图的,而不是偶然的或模仿前人)就可以视作达到第二层级的标志。

第三层级至关重要,它让我们为发起农业
领域和科学领域的更深层次的革命做好了准备,使得我们人类对于地球的改造能力发生了骤变…

使用这组判断标准,我们便可以将问题的三个层级组合成因果关系之梯(见图1.2)。因果关系
之梯是本书的一个重要隐喻,我们将会多次回顾它

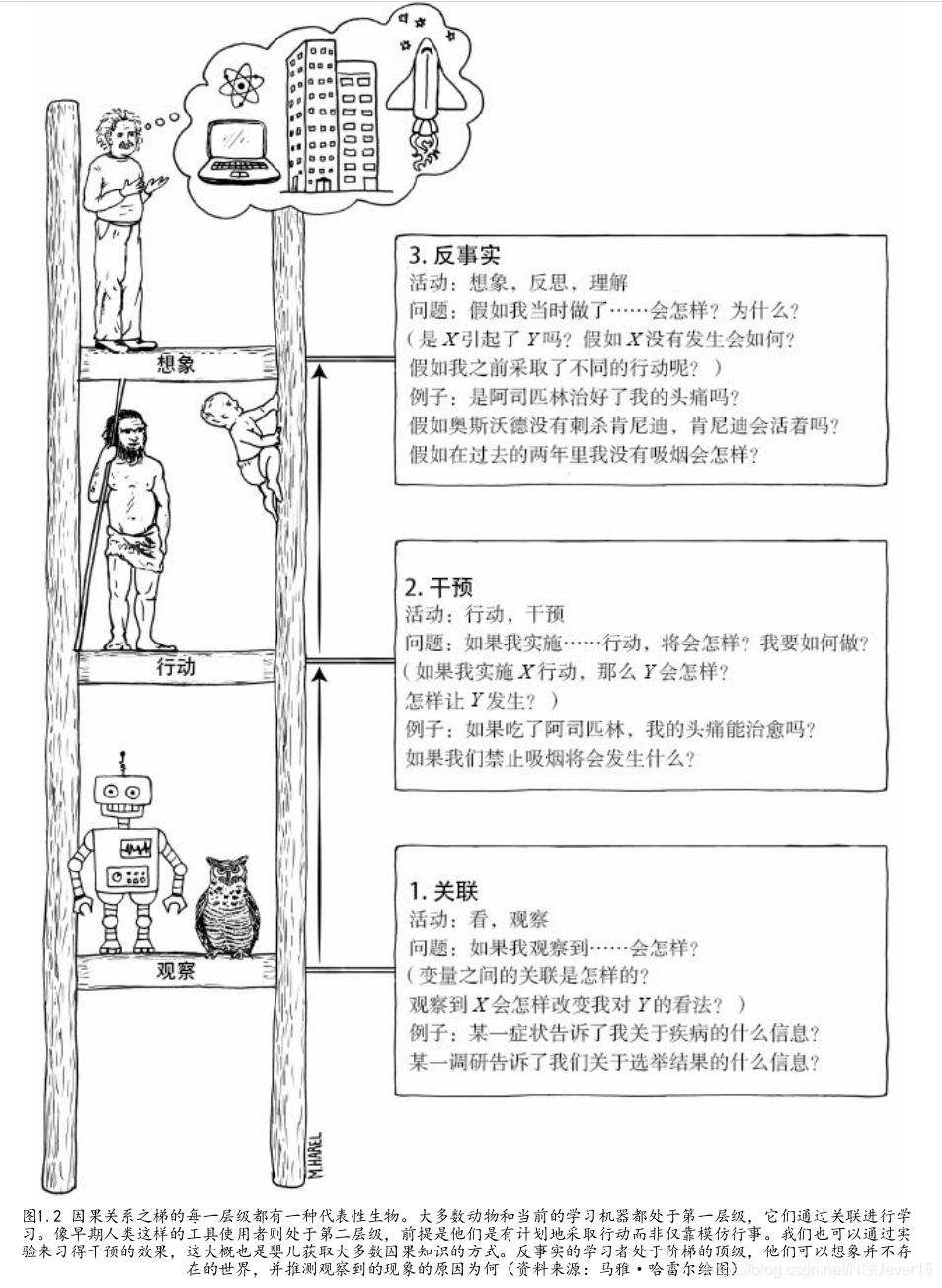
处于第一层级的是关联,在这个层级中
我们通过观察寻找规律。
一只猫头鹰观察到一只老鼠在活动,便开始推测老鼠下一刻可能出现的位置,这只猫头鹰所做的就是通过观察寻找规律。

如果观察到某一事件改变了观察到另一事
件的可能性,我们便说这一事件与另一事件相关联。

因果关系之梯的第一层级要求我们基于被动观察做出预测。
“购买牙膏的顾客同时购买牙线的可能性有多大?”此类问题正是统计学的安身立命之本,统计学家主要通过收集和分析数据给出答案。

首先采集所有顾客购物行为的数据,然后筛选出购买牙膏的顾客,计算他们当中购买牙线的人数
比例。这个比例也称作“条件概率”,用于测算(针对大数据的)“买牙膏”和“买牙线”两种行为之间的关联
程度。用符号表示可以写作P(牙线|牙膏),其中P代表概率,竖线意为“假设你观察到”。

我把当今的人工智能置于因果关系之梯的最底层
强人工智能这一目标是制造出拥有类人智能的机器,让它们能与人类交流并指导人类的探
索方向。而深度学习只是让机器具备了高超的能力,而非智能。这种差异是巨大的,原因就在于后者缺少现实模型。

深度神经网络为拟合函数的复杂性增加了更多的层次,但其拟合过程仍然由原始数据驱动。
处于因果关系之梯最底层的任何运作系统都不可避免地缺乏这种灵活性和适应性.

当我们开始改变世界的时候,我们就迈上了因果关系之梯的更高一层台阶。

无论数据集有多大或者神经网络有多深,
只要使用的是被动收集的数据,我们就无法回答有关干预的问题。

预测干预结果的一种非常直接的方法是在严格控制的条件下进行实验。
一个足够强大的、准确的因果模型可以让我们利用第一层级(关联)的数据来回答第二层级(干预)的问题。没有因果模型,我们就不能从第一层级登上第二层级。
这就是深度学习系统(只要它们只使用了第一层级的数据而没有利用因果模型)永远无法回答干
预问题的原因,干预行动据其本意就是要打破机器训练的环境规则。

因果关系之梯第二层级的典型问题就是:“如果我们实施…行动,将会怎样?” 也
即,如果我们改变环境会发生什么?我们把这样的问题记作P(牙线 |do(牙膏)),它所对应的问题是:
如果对牙膏另行定价,那么在某一价位销售牙线的概率是多少?

第二层级中的另一个热门问题是:“怎么做?”它与“如果我们实施…行动,将会怎样”是同类问题。

(后者是前者的解决方案)

分析原因,现在我的头已经不痛了,但这是为什么?这些问题将我们带到因果关系之梯的最高层,即反事实层级

反事实与数据之间存在着一种特别棘手的关系,因为数据顾名思义就是事实。
回到牙膏的例子,针对这个例子,最高层级的问题是:“假如我们把牙膏的价格提高一倍,则之前买
了牙膏的顾客仍然选择购买的概率是多少?”在这个问题中,我们所做的就是将真实的世界(在真实的世
界,我们知道顾客以当前的价格购买了牙膏)和虚构的世界(在虚构的世界,牙膏价格是当前的2倍)进
行对比。

将反事实置于因果关系之梯的顶层,已经充分表明了我将其视为人类意识进化过程的关键时刻。

半人半狮
是解剖学意义上
的现代人类创造了它,它的出现标志着对先前所有的艺术或工艺品形式的突破。
它的本体是一个只存在于想象中的生物。

从想象的反事实中,我们获得的独特优势是灵活性、反省能力和改善过去行为的能力,更重要的一点是对过去和现在的行为承担责任的意愿。古往今来,我们一直受益于反事实推理。

,因果关系之梯第三层级的典型问题是:“假如我当时做了…会怎样?”和“为什么?”两
者都涉及观察到的世界与反事实世界的比较。
仅靠干预实验无法回答这样的问题。

如果第一层级对应的是
观察到的世界,第二层级对应的是一个可被观察的美好新世界,那么第三层级对应的就是一个无法被观察
的世界(因为它与我们观察到的世界截然相反)。

为了弥合第三层级与前两个层级之间的差距,简言之,我们需要掌握一种理解力,建立一种理论,据此我们就可以预测在
尚未经历甚至未曾设想过的情况下会发生什么

但因果推断的意义还要
更为深远:在掌握了各种法则之后,我们就可以有选择地违背它们,以创造出与现实世界相对立的世界。

迷你图灵测试

图灵测试
一个普通人出于实用目的用打字机与一台计算机交流,如果他无法判断谈话对
象是人还是计算机,那么这台计算机就可以被视作一台思维机器

与其试图编写一个模拟成人
思维的程序,何不尝试编写一个模拟儿童思维的程序?”如果能做到这一点,那么你就可以像教小孩子一样教它了。

图灵错了:儿童的大脑有着丰富的预设机制和预存模板。

在创造出具备孩童智能水平的机器人之前,我们可能的确
无法成功创造出类人智能,而创造出前者的关键要素就是掌握因果关系。

假设我们
有10个因果变量,每个变量只取两个值(0或1),那么我们可以提出大约3000万个关于这些变量的可能问
题,例如:“如果我们看到变量X等于1,而我们让变量Y等于0且变量Z等于1,那么结果变量为1的概率是
多少?”

,很显然,简单
的问题答案列表永远无法让机器模拟儿童的智能,更不用说模拟成人的智能了。

人类的大脑肯定拥有某种简洁的信息表示方式,同时还拥有某种十分有效的程序用以正确解释每个问
题,并从存储的信息表示中提取正确答案。

事实上,这种表示不仅存在,而且具有孩童思维般的简洁性,它就是因果图。

如图1.4所示,我们假设一个犯人将要被行刑队执行枪决。这件事的发生必然会以一连串的事件发生为前提。首先,法院方面要下令处决犯人。命令下达到行刑队队长后,他将指示行刑队的士兵(A和B)执行枪决。我们假设他们是服从命令的专业枪手,只听命令射击,并且只要其中任何一个枪手开了枪,囚犯都必死无疑。

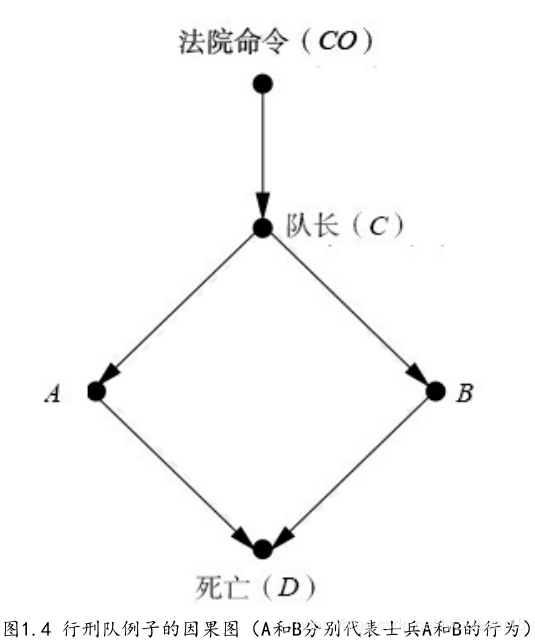
图1.4所示因果图即概括了我刚才讲的故事。每个未知量(CO,C,A,B,D)都是一个真/假
(true/false)变量。例如,D=真,意思是犯人已死;D=假,意思是犯人还活着。CO=假,意思是法院的死
刑命令未签发;CO=真,意思则是死刑命令已签发,以此类推。

借助这个因果图,我们就可以回答来自因果关系之梯不同层级的因果问题了。

关联
即使士兵A的行为不是士兵B做出某一行为的原因(因为从A到B没有箭头),该判
断依然为真。

干预
如果我们希望计算机能理解因果关系,我们就必须教会它如何打破规则,让它懂得“观察到某事
件”和“使某事件发生”之间的区别。

我们需要告诉计算机:“无论何时,如果你想使某事发生,那就删除指
向该事的所有箭头,之后继续根据逻辑规则进行分析,就好像那些箭头从未出现过一样。”

使某事发生就意味着将它从所有其他影响因子中解放
出来,并使它受限于唯一的影响因子——能强制其发生的那个因子。

图1.5表示出了根据这个例子生成的因果图。显然,这种干预会不可避免地导致犯人的死亡。这就是箭头A到D背后的因果作用。

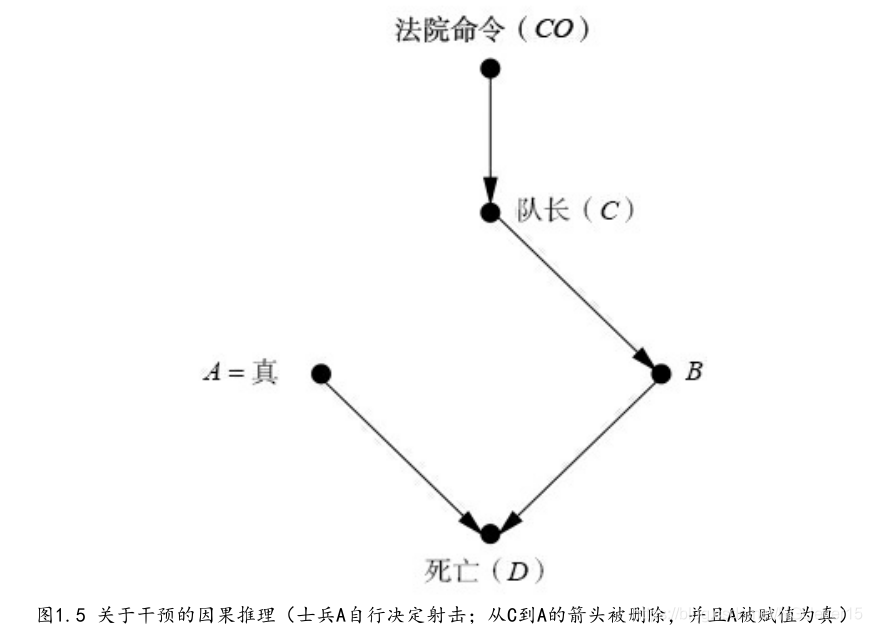
如果我们“看到”A射击,则我们可以下结
论——B也射击了。但是如果A自行“决定”射击,或者如果我们强制“使”A射击,那么在此种情况下,相反的结论才是对的… 这就是“观察到”和“实施干预”的区别

需要注意的是,仅凭收集大数据无助于我们登上因果关系之梯去回答上面的问题。

反事实
最后,为了说明因果关系之梯的第三层级,我们提出一个反事实问题。
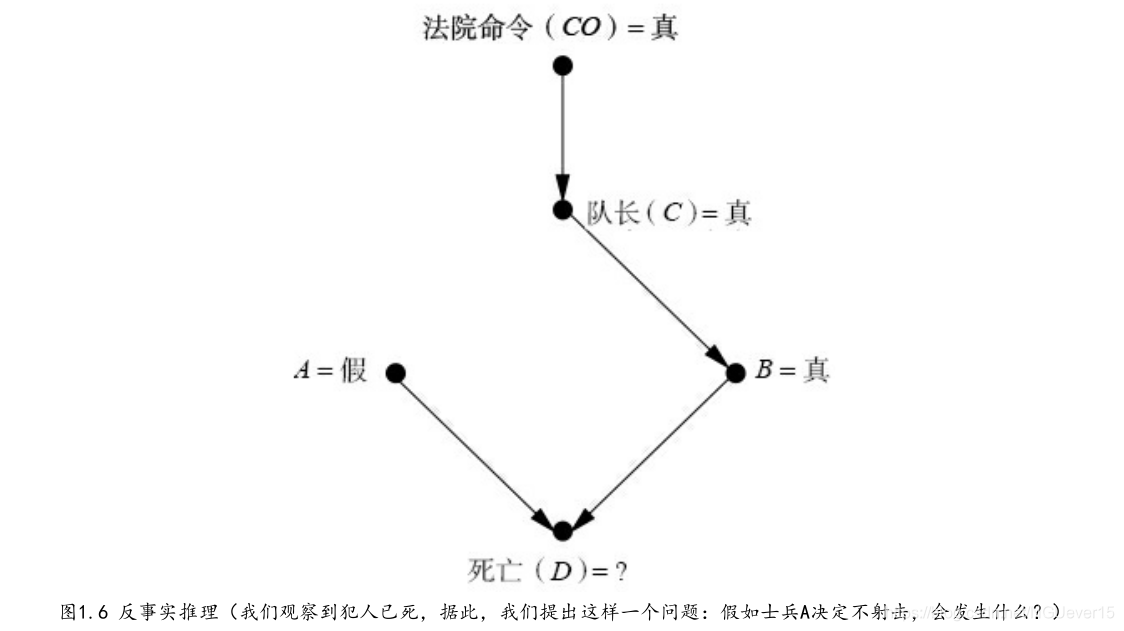
假设犯人现在已倒地身亡,
在虚构世界中,A没有射击,指向A的箭头被去除,这进而又解除了A与C的听
命关系。现在,我们将A的值设置为假,并让A行动之前的所有其他变量的水平与现实世界保持一致。如此一来,这一虚构世界就如图1.6所示。

如上述三个例子所示,我们必须教会计算机如何有选择地
打破逻辑规则。计算机不擅长打破规则,这是儿童的强项。

---

数据显示有更多的人死于天花疫苗,而非死于天花。有些人理所当然地利用这些信息辩
称,应该禁止人们接种疫苗,而不顾疫苗实际上根除了天花,挽救了许多生命的事实。

假设100万儿童中有99%接种了疫苗,1%没有接种。对于接种了疫苗的儿童来说,一方面,他有1%的
可能性出现不良反应,这种不良反应有1%的可能性导致儿童死亡。另一方面,这些接种了疫苗的儿童不可
能得天花。相对的,对于一个未接种疫苗的儿童来说,他显然不可能产生接种后的不良反应,但他有2%的
概率得天花。最后,让我们假设天花的致死率是20%。

按照假设,在100万个孩子中,99万人接种了疫苗,其中有9900人出现了接种后的不良反应,这之中有99人因此死亡。与此同时,那1万
个没有接种疫苗的孩子中,有200人得了天花,其中的40人死于天花。这样一来,死于疫苗接种不良反应
的儿童(99人)就多于死于天花的儿童(40人)了。

反事实问题:“假如我们把疫苗接
种率设为零会怎样?”
100万孩子中2万人会得天
花,4000人会死亡。
在此,我们应该感谢反事实的语言 [3] 让我们避
免了付出如此惨重的代价。

这个例子中学到的最重要的知识是:构建因果模型不仅仅是画箭
头,箭头背后还隐藏着概率。
通常情况下,因果图自身的结构就足够让我们推
测出各种因果关系和反事实关系:简单的或复杂的、确定的或概率的、线性的或非线性的。

在所有三个例子
中,我们都使用了相同的程序:将故事转化成因果图,解读问题,执行与既定问题(干预问题或反事实问
题)相对应的“手术”(如果问题是关联类的,则不需要进行任何“手术”),并使用修改后的因果模型计算
答案。

并且,每次改变故事的时候,我们也不必根据各种新的问题重新训练机器。这一方法具有足够的灵
活性,只要我们能绘制出因果图,我们就能解决问题

因果观都比概率
观更重要。

例如,假设随着时代改变,出现了一种更安全、更有效的疫苗。同时,由于卫生条件和
社会经济条件的改善,人们感染天花的危险也减少了。这些变化将对前文提到的例子中的绝大部分变量的
概率产生极大的影响;但显然,原有的因果图结构仍将保持不变。

如导言所述,同样的被估量(也就是回答相应问题的方法)
将一直有效,并且只要因果图不变,该被估量就可以应用于新数据,并为特定问题生成新的估计值。我猜
想,正是由于具备这种稳健性,人类的直觉才以因果关系而非统计关系为组织的核心。 (导言部分回去重新看)

论概率与因果关系

从赖欣巴哈和萨普斯开始,哲学家们开始使用“概
率提高”的概念来定义因果关系:如果X提高了Y的概率,那么我们就说X导致了Y

例如,当我们说“鲁莽驾驶会导致交通事故”或“你会
因为懒惰而挂科”时

前者只是增加了后者发生的可能性,而非必然会让后者发生。

条件概率表示存在的问题
哲学家几乎无一例外地使
用了条件概率来表示“X提高了Y的概率”,记作P(Y|X)>P(Y)

这种解释是错的,因
为“提高”是一个因果概念,意味着X对Y的因果效应,而公式P(Y|X)>P(Y)只涉及观察和手段,表示的
是“如果我们观察到了X,那么Y的概率就提高了”。

这种概率提高完全可能是由其他因素造成的,比
如Y是X的因,或者其他变量(Z)是它们二者的因

用类似表达式P(Y|X)所表示的概率位于因果关系之梯的第一层级,其不能(靠自己)回答第二层级或第三层级的问题。

X和Y共同的因或称混杂因
子(confounder) [5] 问题,是令哲学家最为烦恼的问题之一。

冰淇淋和犯罪的例子

哲学家努力尝试通过为他们所称的“背景因子”(混杂因子的另一种说法)设置限定条件来修复定义,
并据此建构了表达式P(Y|X,K=k)>P(Y|K=k),其中K代表背景变量。

例如,如果我们只看温度为30°C的日子(K=30),
我们就会发现冰激凌的销售和犯罪率之间不存在任何残留的关联。只有把30°C的日子和0°C的日子进行比较,我们才会产生概率提高的错觉。

然而,对于“哪些变量要放入背景因子集合K中作为条件”这一问题,还没有一个哲学家能够给出一个
令人信服的通用答案。

目前我能给出的提示是,离开因果图,我们是不可能阐明这个定
义的。

拯救概率提高这一概念的正确方法是借助do算子来定义,如果P(Y|do(X))>P(Y),那么我们就
可以说X导致了Y。。由于干预是第二层级的概念,因此这个定义能够体现概率提高的因果解释,也可以让我们借助因果图进行概率推算。

在努力将因果关系的概念数学化(这本身就是一个值得称道的想法)的过程中,哲学家过早地
诉诸其所知的唯一一种用于处理不确定性的语言,即概率语言。

贝叶斯网络适用于一个所有问题都被简化为概率或者(用本章的术语来说就是)变量间的关联程度的世界,它无法自动升级到因果关系之梯的第二层级或第三层级。

我想说明的主要观
点是:概率能将我们对静态世界的信念进行编码,而因果论则告诉我们,当世界被改变时,无论改变是通
过干预还是通过想象实现的,概率是否会发生改变以及如何改变。