繁依Fanyi0

这个屌丝很懒，什么也没留下！

热门标签

动态规划----股票买卖问题（详解）_股票买卖问题算法

作者：繁依Fanyi0 | 2024-05-15 05:17:32

踩

股票买卖问题算法

买卖股票的最佳时机问题介绍：动态规划买卖股票的最佳时机是一个经典的算法问题。该问题的目标是在给定的股票价格数组中，找到最大的利润，即最佳的买入和卖出时间，使得买入时间早于卖出时间。

下面我们通过一些例题，来解决这一类动态规划的问题：

一.买卖股票的最佳时机：

题目链接：121. 买卖股票的最佳时机 - 力扣（LeetCode）
题目描述：
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

①.动态规划解法：

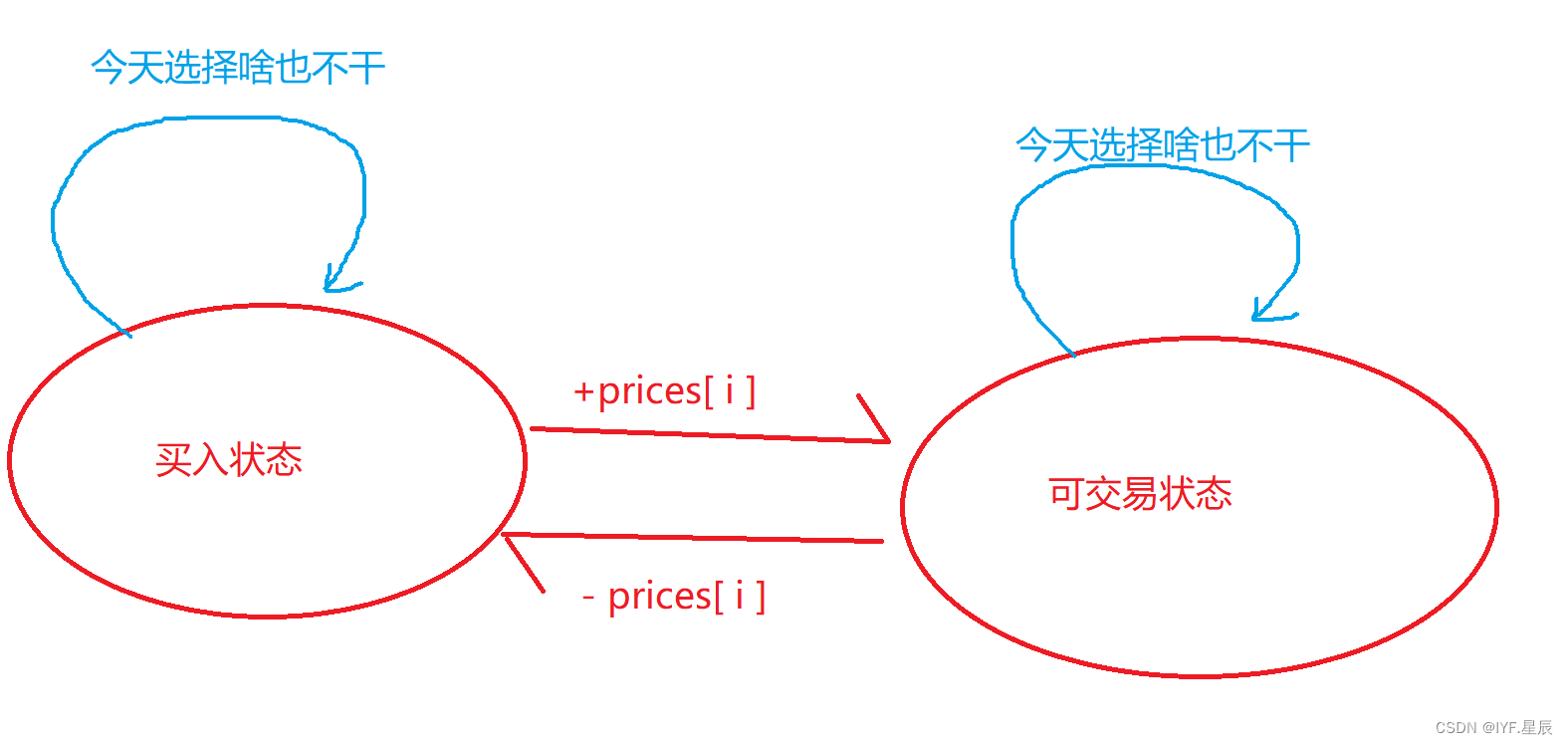
一.状态表示dp[ i ][ j ]：下标为 i 这一天结束的时候，手上持股状态为 j 时，我们持有的最大利润。这里我们定义状态 j （两种情况）分别为：
0 买入状态
1 可交易状态
二.状态转移方程：
dp[ i ][ 0 ] = Math.max( dp[ i - 1 ][ 0 ], -prices[ i ]) ; ①.在前面一天已经是买入状态，今天选择什么也不干，今天结束后，是买入状态。②.前面是可交易状态，今天选择买入，则今天结束后是买入状态，这里注意不是dp[ i - 1][ 1 ] - prices[ i ];因为只能交易一次，如果今天选择买入，那后面一定要卖出（这算一次交易),此时才可能有最大利润。则前面不能有交易，利润为0.
dp[ i ][ 1 ] = Math.max( dp[ i - 1][ 1 ],dp[ i - 1][ 0 ] + prices[ i ]);①.前面一天是可交易状态，今天选择什么也不干，今天结束后是可交易状态。②.前面一天是买入状态，今天选择卖出，今天结束后是可交易状态。
三.初始化：根据状态表示：
dp[ 0 ][ 0 ] = - prices[ 0 ];第一天选择买入，此时利润为 - prices[ 0 ]
dp[ 0 ][ 1 ] = 0;第一天选择什么也不干或则交易一次，此时的利润为0;
四.填表顺序：根据状态转移方程，从左往右，从上往下填写.
五.返回值：dp[ n - 1 ][ 1 ];n为prices数组的长度,最后一天结束后，是可交易状态，此时为最大利润.

各个状态关系图：

代码详解：
class Solution {
         // 1. 创建 dp 表
        // 2. 初始化
       // 3. 填表
       // 4. 返回值
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][2];
        //初始化
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
 
        for(int i = 1;i < n;i++){
            //注意这里不是dp[i - 1][1] - prices[i];
            dp[i][0] = Math.max(dp[i - 1][0], - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);
        }
        //返回值
        return dp[n - 1][1];
    }
}

②.暴力解法（相对简单这里给出解题过程）：

代码详解：


class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE;
        int profit = 0;
        for(int price : prices){
            cost = Math.min(cost,price);
            profit = Math.max(profit,price - cost);
        }
        return profit;
    }
}

运行结果：

二.买卖股票的最佳时机含冷冻期：

题目链接：309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）
问题描述：
给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

动态规划解法：

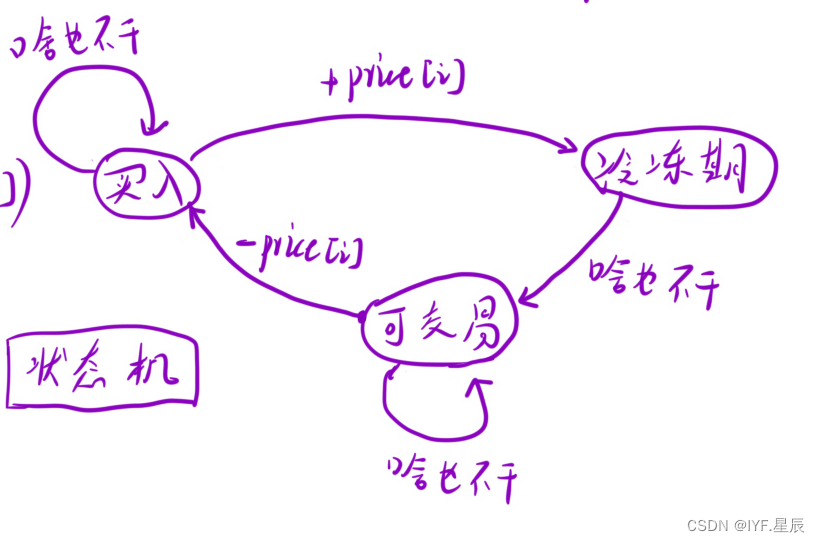
一.状态表示：dp[ i ][ j ]:由于有「买⼊」「可交易」「冷冻期」三个状态，因此我们可以选择⽤三个数组，其中：

dp[i][0] 表⽰：第 i 天结束后，处于「买⼊」状态，此时的最⼤利润；
dp[i][1] 表⽰：第 i 天结束后，处于「可交易」状态，此时的最⼤利润；
dp[i][2] 表⽰：第 i 天结束后，处于「冷冻期」状态，此时的最⼤利润

二.状态转移方程：

dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); ①.前一天是买入状态，今天啥也不做，今天结束后是买入状态②.前面一天是可交易状态，今天选择买入，今天结束后是买入状态。
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]); ①.前面一天是可交易状态，今天啥也不干，今天结束后是可交易状态②.前面一天是冷冻期，今天啥也不干，今天过后是可交易状态
dp[i][2] = dp[i - 1][0] + prices[i]；前面一天是买入状态，今天选择卖出，今天过后是冷冻期

三.初始化：

dp[0][0] = - prices[0] ； dp[0][1] = 0 ； dp[0][2] = 0;

四.填表顺序：从左往右，从上往下，依次填写三个表

五.返回值：状态转移方程三者的最大值：

max(dp[n - 1][1], dp[n - 1] [2]);dp[n - 1][0]不可能是最大值，这里不用考虑进去（如果考虑进去了也没关系）

各个状态关系图：

代码详解：
class Solution {
      // 1. 创建 dp 表
        // 2. 初始化
       // 3. 填表
       // 4. 返回值
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][3];
        dp[0][0] = -prices[0];
        for(int i = 1;i < n;i++){
            dp[i][0] = Math.max(dp[i - 1][0],dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][2]);
            dp[i][2] = dp[i - 1][0] + prices[i];
        }
        return Math.max(dp[n - 1][1],dp[n - 1][2]);
    }
}

运行结果：

三.买卖股票的最佳时期含⼿续费：

题目链接：714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

题目描述：

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

动态规划解法：

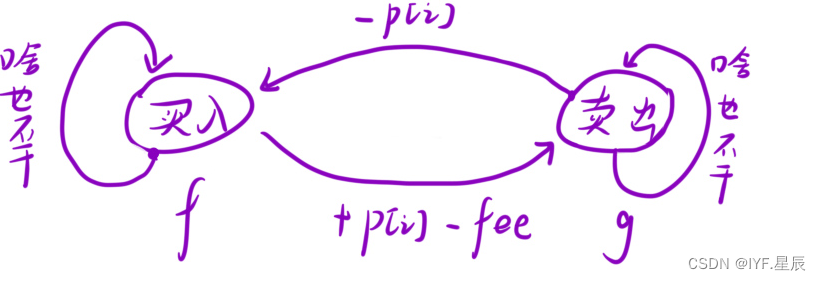
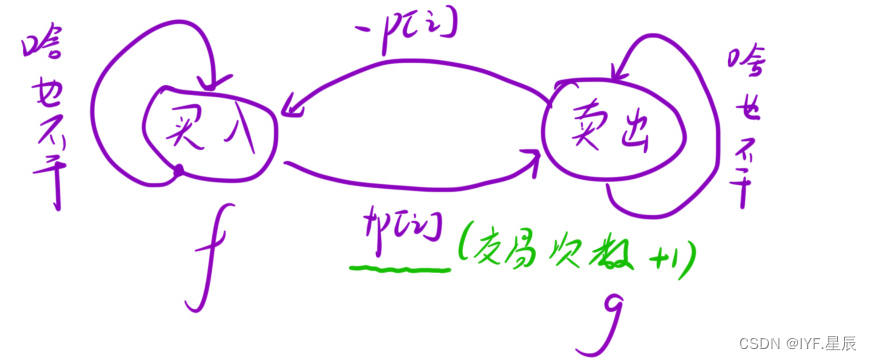
一.状态表示：由于有「买⼊」「可交易」两个状态，因此我们可以选择⽤两个数组来定义我们的状态（或则一个二维数组也行），其中：

f[i] 表⽰：第 i 天结束后，处于「买⼊」状态，此时的最⼤利润；
g[i] 表⽰：第 i 天结束后，处于「卖出」状态，此时的最⼤利润.

二.状态转移方程：我们选择在「卖出」的时候，⽀付这个⼿续费，那么在「买⼊」的时候，就不⽤再考虑⼿续费的问题（完成一次交易支付手续费）：

f[i] = max(f[i - 1], g[i - 1] - prices[i]) ；①.在 i - 1 天「持有」股票，第 i 天啥也不⼲。此时最⼤收益为 f[i - 1] ；②.在 i - 1 天的时候「没有」股票，在第 i 天买⼊股票。此时最⼤收益为 g[i - 1] - prices[i]) ；
g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);①.在 i - 1 天「持有」股票，但是在第 i 天将股票卖出。此时最⼤收益为： f[i - 1] + prices[i] - fee) ，记得⼿续费；②.在 i - 1 天「没有」股票，然后第 i 天啥也不⼲。此时最⼤收益为： g[i - 1]

三.初始化：由于需要⽤到前⾯的状态，因此需要初始化第⼀个位置:

对于 f[0] ，此时处于「买⼊」状态，因此 f[0] = -prices[0]
对于 g[0] ，此时处于「没有股票」状态，啥也不⼲即可获得最⼤收益，因此 g[0] = 0

四.填表顺序：从左到右两个表一起填

五.返回值：应该返回「卖出」状态下，最后⼀天的最⼤值收益： g[n - 1]

代码详解：
class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = -prices[0];
        for(int i = 1;i < n;i++){
            f[i] = Math.max(f[i - 1],g[i - 1] - prices[i]);
            g[i] = Math.max(g[i - 1],f[i - 1] + prices[i] - fee);
        }
        return Math.max(f[n - 1],g[n - 1]);
    }
}

运行结果：

四.买卖股票的最佳时机III:

题目链接：123. 买卖股票的最佳时机 III - 力扣（LeetCode）

题目描述：

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

动态规划解法：

一.状态表示：由于有「买⼊」「可交易」两个状态，因此我们可以选择⽤两个数组。但是这道题⾥⾯还有交易次数的限制，因此我们还需要再加上⼀维，⽤来表⽰交易次数。其中：

f[i][j] 表⽰：第 i 天结束后，完成了 j 次交易，处于「买⼊」状态，此时的最⼤利润；
g[i][j] 表⽰：第 i 天结束后，完成了 j 次交易，处于「卖出」状态，此时的最⼤利润。

二.状态转移方程：

f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);①.在 i - 1 天的时候，交易了 j 次，处于「买⼊」状态，第 i 天啥也不⼲即可。此时最⼤利润为： f[i - 1][j] ；②.在 i - 1 天的时候，交易了 j 次，处于「卖出」状态，第 i 天的时候把股票买了。此时的最⼤利润为： g[i - 1][j] - prices[i] 。
g[i][j] = g[i - 1][j];

if(j > 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);

①.在 i - 1 天的时候，交易了 j 次，处于「卖出」状态，第 i 天啥也不⼲即可。此时的最⼤利润为： g[i - 1][j] ；

②.在 i - 1 天的时候，交易了 j - 1 次，处于「买⼊」状态，第 i 天把股票卖了，然后就完成了 j ⽐交易。此时的最⼤利润为： f[i - 1][j - 1] + prices[i] 。但是这个状态不⼀定存在，要先判断⼀下。

三.初始化：

当处于第 0 天的时候，只能处于「买⼊过⼀次」的状态，此时的收益为 -prices[0] ，因此 f[0][0] = - prices[0] 。
为了取 max 的时候，⼀些不存在的状态「起不到⼲扰」的作⽤，我们统统将它们初始化为 - INF （⽤ INT_MIN 在计算过程中会有「溢出」的⻛险，这⾥ INF 折半取 0x3f3f3f3f ，⾜够⼩即可）

四.填表顺序：从「上往下填」每⼀⾏，每⼀⾏「从左往右」，两个表「⼀起填」。

五.返回值：返回处于「卖出状态」的最⼤值，但是我们也「不知道是交易了⼏次」，因此返回 g 表最后⼀⾏的最⼤值。

代码详解：
class Solution {
    static int INF = -0x3f3f3f3f;
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] f = new int[n][3];
        int[][] g = new int[n][3];
        //1.
        f[0][0] = -prices[0];
        for(int i = 1;i < f[0].length;i++){
            f[0][i] = INF;
        }
        for(int j = 1;j < g[0].length;j++){
            g[0][j] = INF;//Integer.MIN_VALUE/2
        }
        
        //2.
        for(int i = 1;i < n;i++){
            for(int j = 0;j < 3;j++){
                f[i][j] = Math.max(f[i - 1][j],g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j > 0){
                    g[i][j] = Math.max(g[i][j],f[i - 1][j - 1] + prices[i]);
                }
            }
        }
        int res = Integer.MIN_VALUE;
        for(int j = 0;j < 3;j++){ 
           res = Math.max(res,g[n - 1][j]);
        }
        return res;
    }
}

运行结果：

五.买卖股票的最佳时机IV:

题目链接：188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

题目描述：

给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

动态规划解法：

一.状态表示：为了更加清晰的区分「买⼊」和「卖出」，我们换成「有股票」和「⽆股票」两个状态：

f[i][j] 表⽰：第 i 天结束后，完成了 j 笔交易，此时处于「有股票」状态的最⼤收益；
g[i][j] 表⽰：第 i 天结束后，完成了 j 笔交易，此时处于「⽆股票」状态的最⼤收益

二.状态转移方程：

f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);①.在 i - 1 天的时候，⼿⾥「有股票」，并且交易了 j 次。在第 i 天的时候，啥也不⼲。此时的收益为 f[i - 1][j] ；②.在 i - 1 天的时候，⼿⾥「没有股票」，并且交易了 j 次。在第 i 天的时候，买了股票。那么 i 天结束之后，我们就有股票了。此时的收益为 g[i - 1][j] - prices[i];
g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);①.在 i - 1 天的时候，⼿⾥「没有股票」，并且交易了 j 次。在第 i 天的时候，啥也不⼲。此时的收益为 g[i - 1][j] ；②.在 i - 1 天的时候，⼿⾥「有股票」，并且交易了 j - 1 次。在第 i 天的时候，把股票卖了。那么 i 天结束之后，我们就交易了 j 次。此时的收益为 f[i - 1][j - 1] + prices[i] ；

三.初始化：

当处于第 0 天的时候，只能处于「买⼊过⼀次」的状态，此时的收益为 -prices[0] ，因此 f[0][0] = - prices[0]
为了取 max 的时候，⼀些不存在的状态「起不到⼲扰」的作⽤，我们统统将它们初始化为 - INF （⽤ INT_MIN 在计算过程中会有「溢出」的⻛险，这⾥ INF 折半取 0x3f3f3f3f ，⾜够⼩即可）

四.填表顺序：从上往下填每⼀⾏，每⼀⾏从左往右，两个表⼀起填。

五.返回值：返回处于卖出状态的最⼤值，但是我们也不知道是交易了⼏次，因此返回 g 表最后⼀⾏的最⼤值

代码详解：
class Solution {
    static int INF = -0x3f3f3f3f;
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        int[][] f = new int[n][k + 1];
        int[][] g = new int[n][k + 1];
        //1.
        f[0][0] = -prices[0];
        for(int i = 1;i < f[0].length;i++){
            f[0][i] = INF;//->防止越界g[i - 1][j] - prices[i];
        }
        for(int j = 1;j < g[0].length;j++){
            g[0][j] = INF;//Integer.MIN_VALUE/2
        }
        
        //2.
        for(int i = 1;i < n;i++){
            for(int j = 0;j < k + 1;j++){
                f[i][j] = Math.max(f[i - 1][j],g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j > 0){
                    g[i][j] = Math.max(g[i][j],f[i - 1][j - 1] + prices[i]);
                }
            }
        }
        int res = Integer.MIN_VALUE;
        for(int j = 0;j < k + 1;j++){ 
           res = Math.max(res,g[n - 1][j]);
        }
        return res;
    }
}

运行结果：

结语： 写博客不仅仅是为了分享学习经历，同时这也有利于我巩固知识点，总结该知识点，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注，你们的鼓励是我创作的最大动力！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/571703

动态规划----股票买卖问题（详解）_股票买卖问题 算法

一.买卖股票的最佳时机：

二.买卖股票的最佳时机含冷冻期：

三.买卖股票的最佳时期含⼿续费：

四.买卖股票的最佳时机III:

五.买卖股票的最佳时机IV:

动态规划----股票买卖问题（详解）_股票买卖问题算法