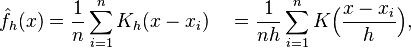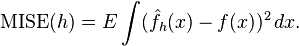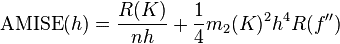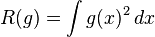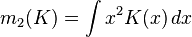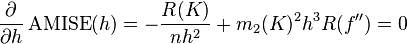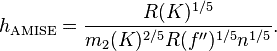核密度估计（Kernel density estimation）

核密度估计（Kernel density estimation），是一种用于估计概率密度函数的非参数方法，为独立同分布F的n个样本点，设其概率密度函数为f，核密度估计为以下：

K(.)为核函数（非负、积分为1，符合概率密度性质，并且均值为0），h>0为一个平滑参数，称作带宽(bandwidth)，也看到有人叫窗口。K_h(x) = 1/h K(x/h). 为缩放核函数(scaled Kernel)。有很多种核函数，uniform,triangular, biweight, triweight, Epanechnikov,normal,等。各种核函数的图形如下：

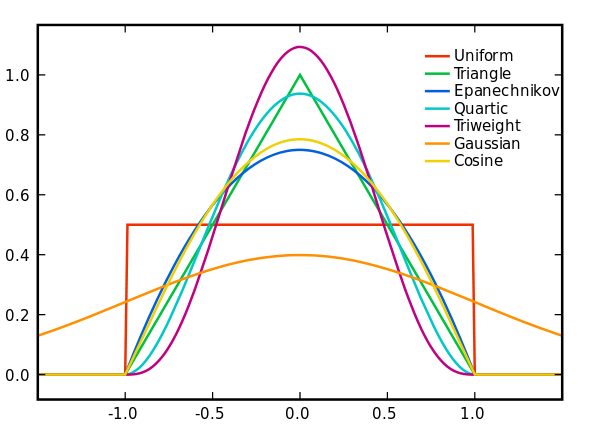
  Epanechnikov 内核在均方误差意义下是最优的，效率损失也很小。由于高斯内核方便的数学性质，也经常使用 K(x)= ϕ(x)，ϕ(x)为标准正态概率密度函数。核密度估计与直方图很类似，但相比于直方图还有光滑连续的性质。下图为直方图与核函数估计对 x₁ = −2.1, x₂ = −1.3, x₃ = −0.4, x₄ = 1.9, x₅ = 5.1, x₆ = 6.2 六个点的“拟合”结果。

在直方图中，横轴间隔为2，数据落到某个区间，此区间y轴增加1/12。在核密度估计中，不放另正态分布方差为2.25，红色的虚线表示由每一个数据得到的正态分布，叠加一起得到核密度估计的结果，蓝色表示。

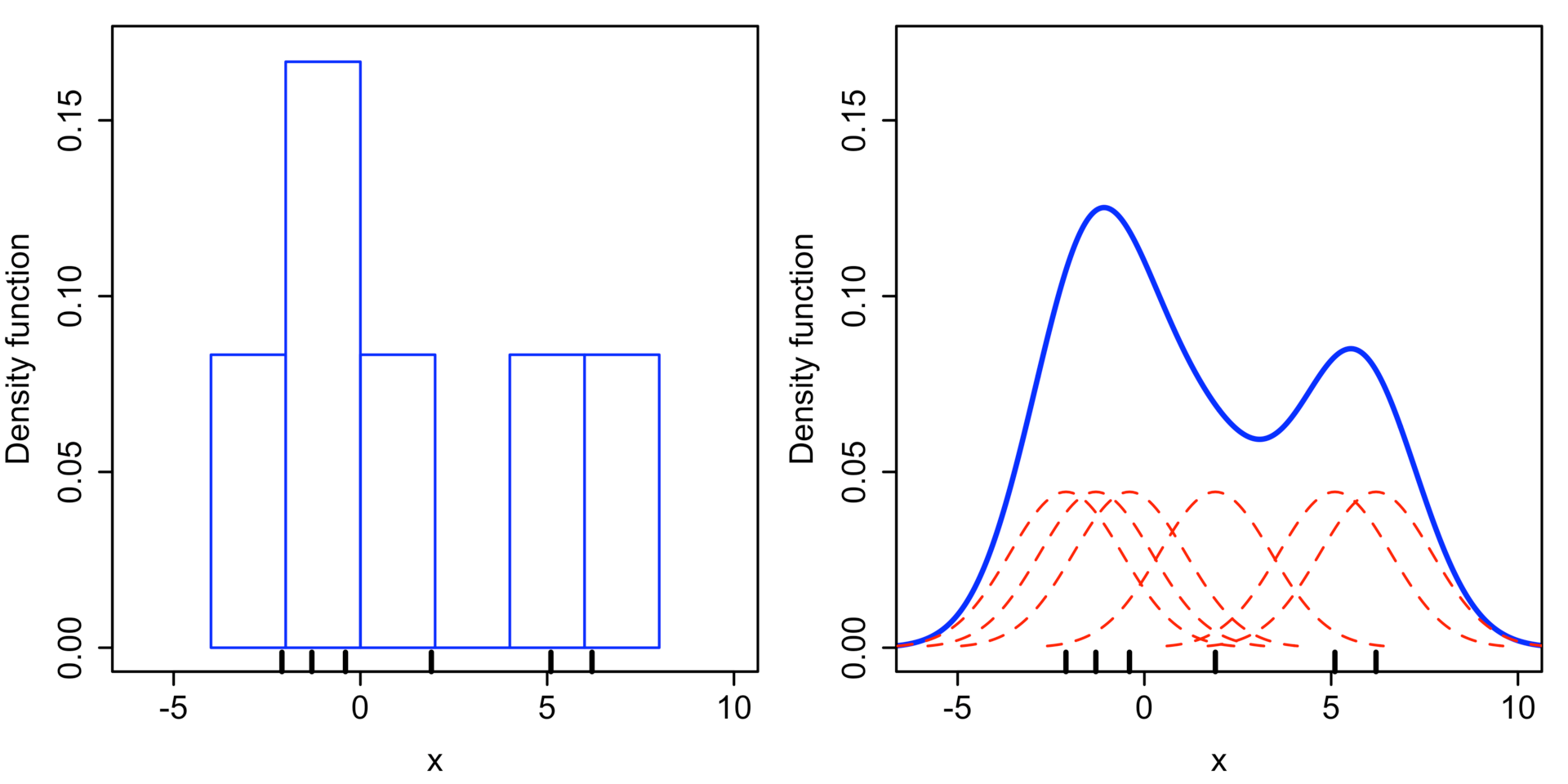
        那么问题就来了，如何选定核函数的“方差”呢？这其实是由h来决定，不同的带宽下的核函数估计结果差异很大，如下图：

（Kernel density estimate (KDE) with different bandwidths of a random sample of 100 points from a standard normal distribution. Grey: true density (standard normal). Red: KDE with h=0.05. Black: KDE with h=0.337. Green: KDE with h=2.）

不同的带宽得到的估计结果差别很大，那么如何选择h？显然是选择可以使误差最小的。下面用平均积分平方误差（mean intergrated squared error）的大小来衡量h的优劣。

在weak assumptions下，MISE (h) =AMISE(h) + o(1/(nh) + h⁴) ，其中AMISE为渐进的MISE。而AMISE有，

，

其中，

，

为了使MISE(h)最小，则转化为求极点问题，

当核函数确定之后，h公式里的R、m、f''都可以确定下来，有（h_{AMISE ~ n^−1/5}），AMISE(h) = O(n^−4/5)。

        如果带宽不是固定的，其变化取决于估计的位置（balloon  estimator）或样本点（逐点估计pointwise estimator），由此可以产产生一个非常强大的方法称为自适应或可变带宽核密度估计。