【同济子豪兄斯坦福CS224W中文精讲】学习笔记二

人工设计特征+机器学习
需要解决的问题：使用向量表示图数据中的节点、连接、全图，那么向量中的特征是如何得到的，特征是根据什么设计出来的？
目标：从nodes/links/graphs中分别抽取D个特征，编码为D维向量
关于特征：特征可以是图结构的自带语义属性或结构信息，由于语义属性vary from task to task，因此我们这里只考虑结构信息做feature engeering
为了解释的简易性，这里的图考虑的是无向图

节点层面的特征工程

目标：设计的向量能够捕捉节点邻域上的结构信息和节点在网络中的位置
常用的特征构造目标：node degree、node centrality、 clustering coefficient、graphlets

分析不同的节点特征应用：
importance-based features:用来推测图中有影响力的节点，具体应用如predicting celebrity users in a social network
structure-based features:用来推测途中各个节点的作用，具体应用如predict protein functionality in a protein-protein interaction network

node degree $k_v$

用节点的度来表示节点信息
计算：使用全一向量右乘邻接矩阵

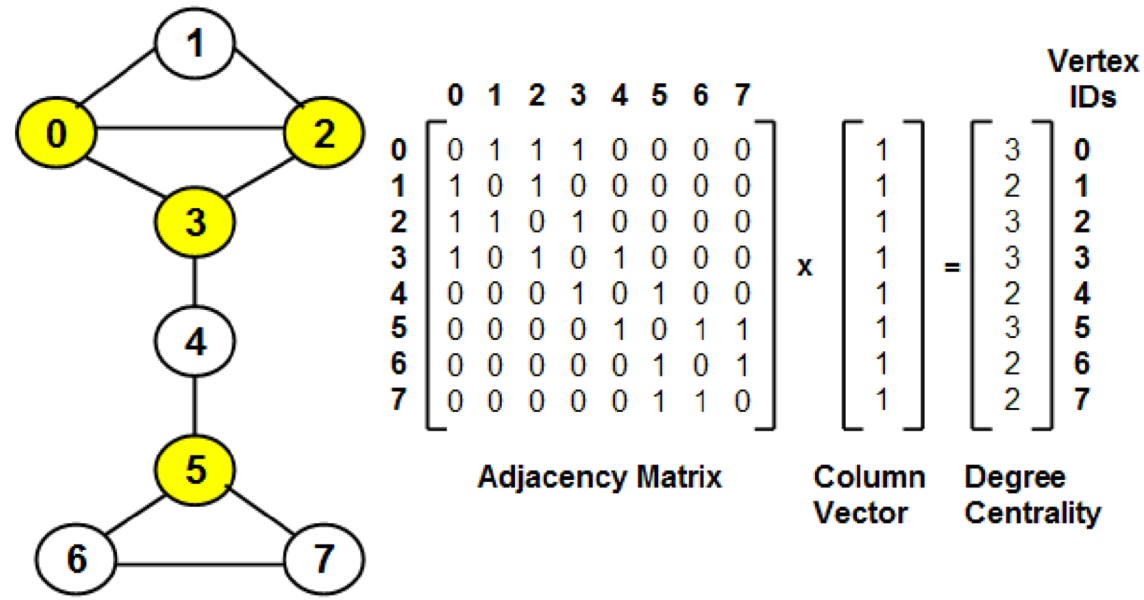
问题：将所有节点视为相同的，没有考虑各个节点的重要性"只看圈子人数，不看圈子质量"

node centrality $c_v$

几种衡量节点重要性的方法：Eigenvector centrality、Betweenness centrality、Closeness centrality

Eigenvector centrality

基本假设：如果一个节点v与很多重要的节点相连，则我们可以说节点v也是重要的。于是我们使用节点v的邻接节点重要度之和作为v的重要度
$$c_v=\frac{1}{\lambda }\sum _{\mu \in N(v)}{c}_{\mu }$$
(这里的$\lambda$是归一化系数，一般取邻接矩阵$A$的最大特征值)
使用矩阵形式改写
$$\lambda c=Ac$$

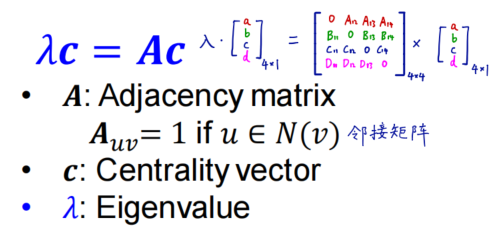
如何理解？
$c$是由各个节点重要性得分排列成的向量，对邻接矩阵，若两个节点相连则对应位置为1，否则为0。由于$A$中每一个行向量代表一个节点，$Ac$ 就能实现$A$中各节点重要性计算。举个例子，节点$v$的邻接情况为(1, 0, 1, 0)，表示v与第1，第3节点邻接，此向量与$c$做数量积的结果为$a\ast 1+b\ast 0+c\ast 1+d\ast 0$ 得到v的重要性为$a+c$
使用最大特征值对应eigenvector作为各个节点的重要性得分

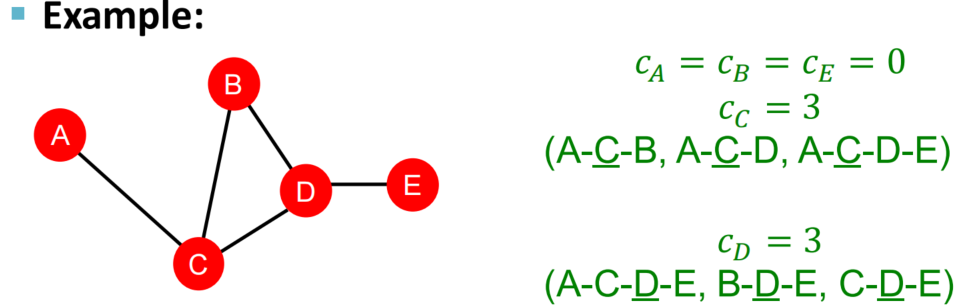
Betweenness centrality

假设：如果一个节点处在多个最短路径上，则这个节点重要性得分高 “交通咽喉，必经之地”
$$c_v=\sum _{s\ne v\ne t}\frac{x}{y}$$
公式解释：x指shortest paths between s and t that contain v， 即图中有多少对节点的最短路径途经v
y指shortest paths between s and t， 即图中两两节点对数

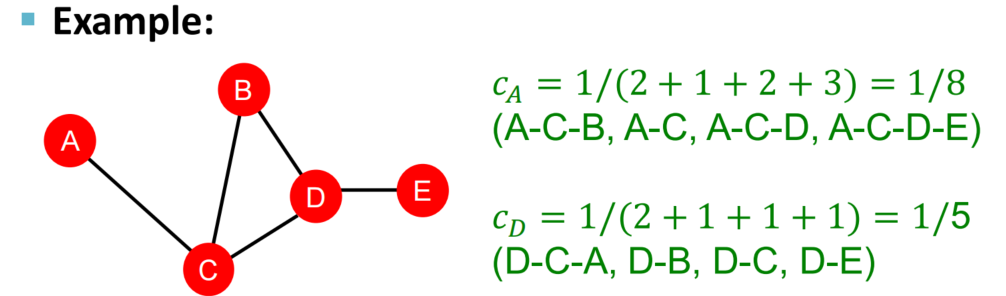
Closeness centrality

假设：如果一个节点到其他所有节点的距离很短，则这个节点被认为是重要的
$$c_v=\frac{1}{{\sum }_{\mu \ne v}p}$$
公式解释：p指shortest path length between $\mu$ and $v$ 即节点u到节点v的最短路径长度求和

clustering coefficient

集群系数：衡量节点的邻接节点的连接程度 “有多抱团”
$$e_v=\frac{t}{C_{k_v}^2}$$
公式说明：t指edges among neighboring nodes ， 即v节点的相邻节点中两两相连个数，也即其中的三角形个数
$C_{k_v}^2$指v节点相邻节点两两对数

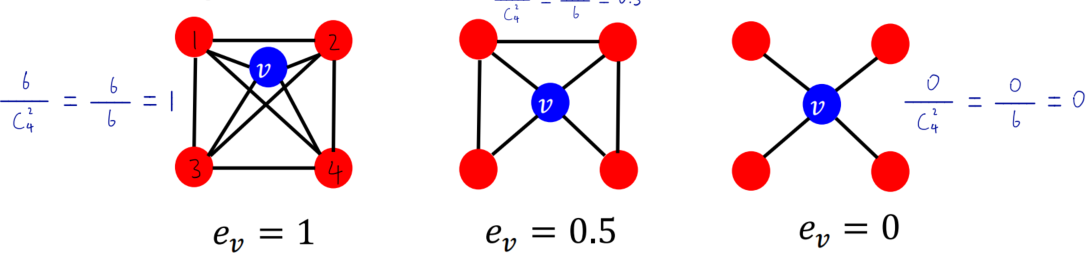
集群系数考虑的是自我中心网络中三角形个数

graphlets

通过pre-specified subgraphs来探究节点邻域上的结构信息(a measure of a node’s network topology)
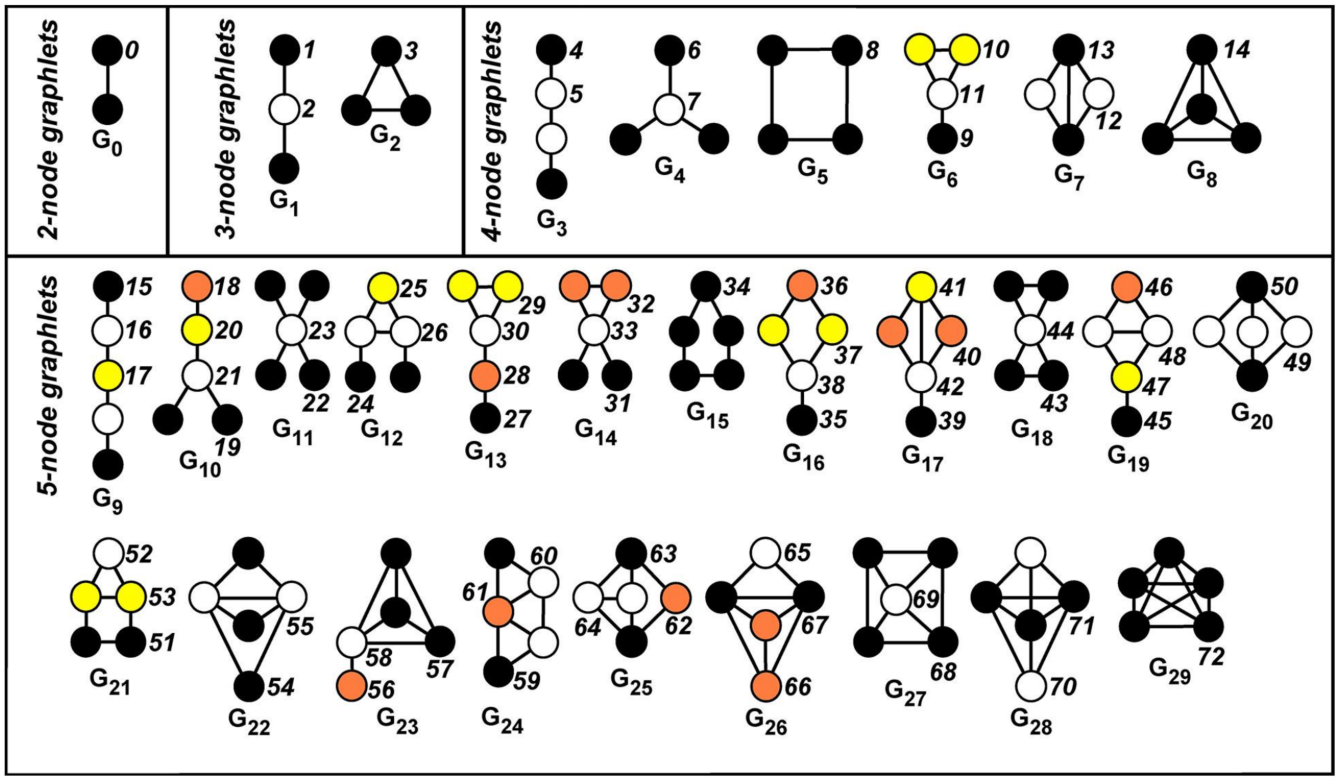
首先我们需要限定讨论范围即节点数目，考虑在节点数目限制之下的subgraphs的可能结构，在这每一个结构中的节点扮演着不同的角色，从而实现通过count一个节点扮演的各种角色的数目来捕捉节点的邻域结构信息。一种节点角色对应一个graphlet
下面是一个5-node以内的subgraph结构及可能的节点角色

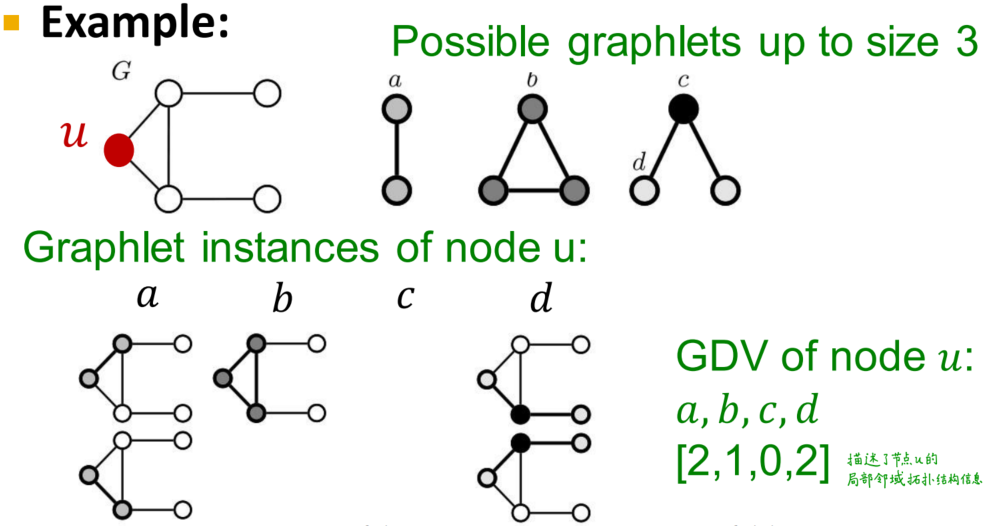
GDV(Graphlet Degree Vector)：a count vector of graphlets rooted at a given node 将各种可能的图拓扑结构信息进行计数统计组成向量

连接层面的特征工程

通过已知连接补全未知连接
解决办法：node pairs with no existing links are ranked, the top K node pairs are predicted
问题关键：design features for a pair of nodes

两种link prediction task的范式

第一种 missing at random
针对静态图，比如蛋白质分子结构预测
第二种 使用over time的数据 利用历史数据预测后来的数据
我们有$G[t_0,t_0^{\prime }]$的数据，需要预测$G[t_1,t_1^{\prime }]$最有可能的边数据
针对的是动态图，比如论文引用，社交网络等

如何设计编码向量

distance-based 依据两节点距离

计算两节点之间的最短路径长度

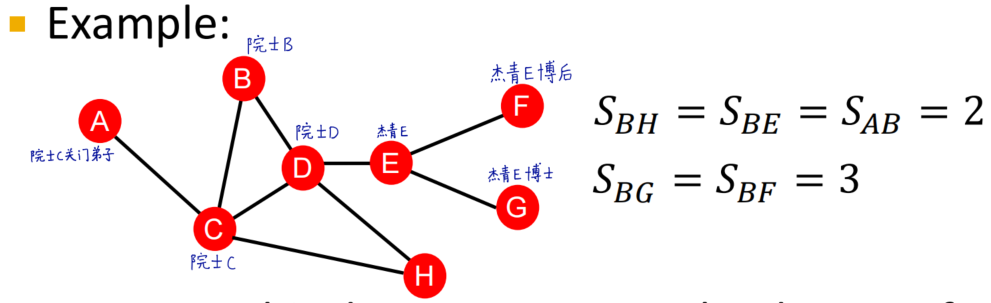
存在的问题？
只关注了两节点的距离远近而没有考虑两个节点的邻域重叠程度(the degree of neighborhood overlap)。在上面的例子中，我们可以看到B和H有两个公共节点，而B和A、E均只有一个公共节点

local neighborhood 利用两节点局部连接信息

通过不同的系数计算捕捉两节点的邻域重叠程度
Common neighbors:公共节点数目
Jaccard’s coefficient:两节点邻域节点的交并比
Adamic-Adar index:考虑公共好友的社交属性

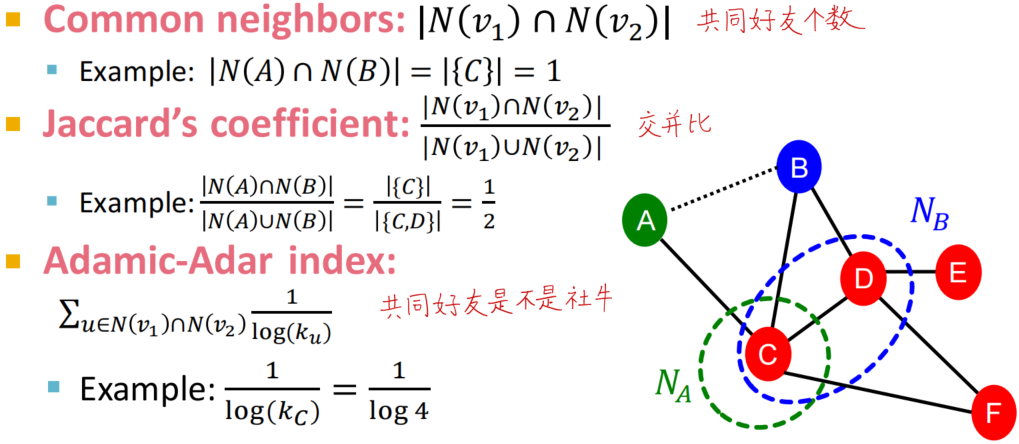
存在的问题？
只考虑两节点邻域信息无法处理没有公共节点的两节点情况，会得到一个全零向量

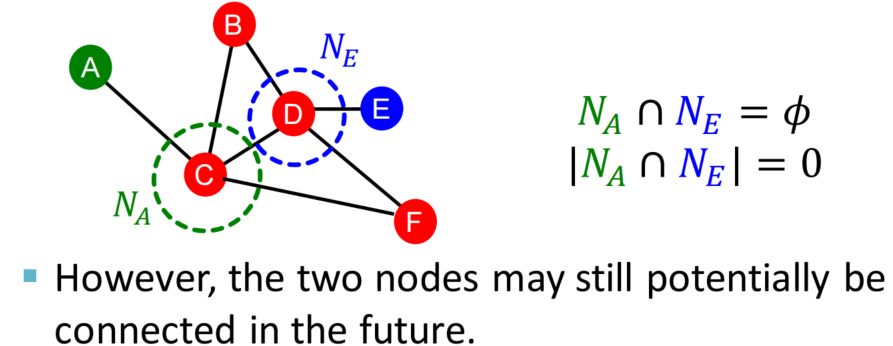
global neighborhood 利用两节点在全图的连接信息

衡量方法：使用Katz index，计算两节点之间任意长度的路径总数目(sum over all walk lengths)
计算Katz index的方法：使用邻接矩阵的幂运算
为了计算Katz index，我们需要先考虑两节点之间长度为k的路径数目的计算
考虑邻接矩阵，$A_{\mu v}=1$ 如果$\mu$ 和v两节点之间有长度为1的路径
考虑两节点之间长度为2的路径，其应该是从节点$\mu$到某距离为1的节点$x$，再从节点$x$到与之距离为1的节点v。因而我们可以写出
$$P_{\mu v}^{(2)}=\sum _i{A}_{\mu i}\ast P_{iv}^{(1)}=\sum _i{A}_{\mu i}\ast A_{iv}=A_{\mu v}^2$$
公式说明：这里使用$P_{\mu v}^{(k)}$表示图中节点$\mu$到节点v长度为k的路径数目

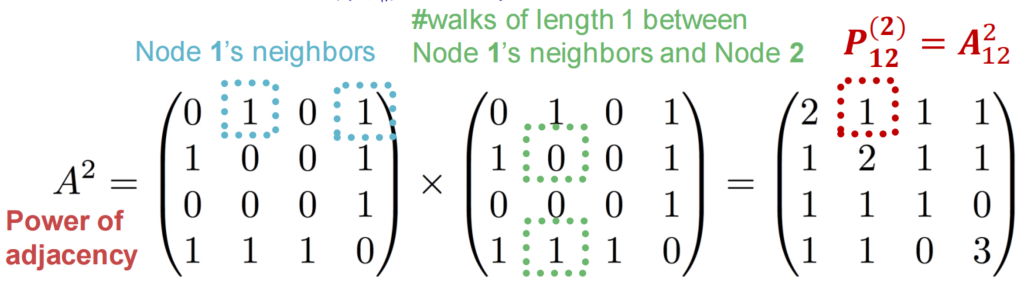
通过数学归纳法，我们可以得到$A^k$结果中对应位置上的数值就为对应两节点之间长度为k的路径数目

将两节点间的所有路径长度进行加和
$$S_{v_1{v}_2}=\sum _{l=1}^{\infty }{\beta }^l{A}_{v_1{v}_2}^l$$
公式说明：$\beta$是折减系数，直观地说就是越长的路径其长度贡献会减少

全图层面的特征工程

目标：从graph中提取D维向量，反应全图的结构特点

Graph Kernel的思想

bag of nodes的方法
从文字序列编码的Bag-of-Words迁移过来，将图中nodes 与 语句中的words类比
缺点：只看节点有没有， 不看连接结构，反映信息不完整

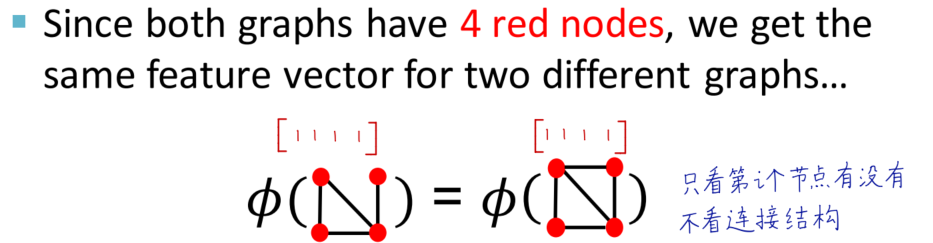
简单地使用bag of nodes不能将以上两个图区分开，考虑使用bag of node degrees。看特定degree的node数目进行编码

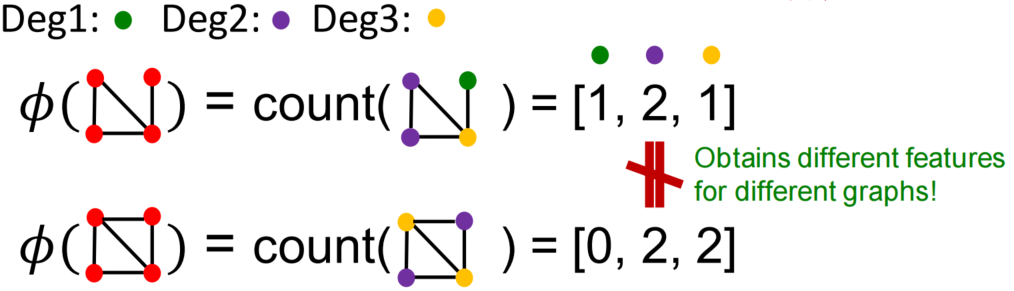
拓展开来，事实上，Graphlet Kernel和Weisfeiler-Lehman(WL) Kernel都是使用了Bag-of-what来对全图进行编码，只是这些Kernel方法中的what会更加复杂

使用graphlet features

首先我们需要了解什么是graphlet-of-graph，即节点个数特定的子图模式
$$g_G=(g_1,g_2,...,g_{n_k})$$
公式说明：nodes个数为k的各个子图模式计数的向量，称为graphlet count vector，满足
$$(g_G{)}_i=g_i\subseteq G$$
公式说明： i = 1,2,…, $n_k$，统计的是第i个graphlet在全图中的个数
举个例子：

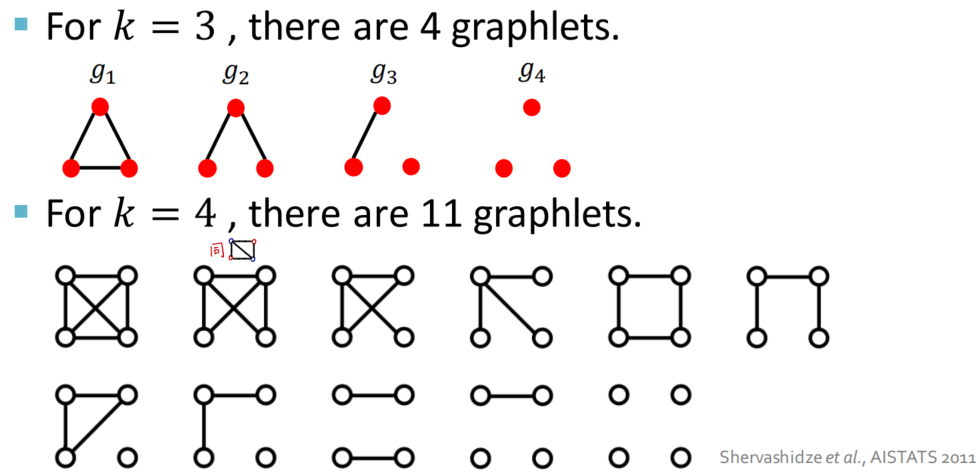
需要区别graphlet-of-node和graphlet-of-graph：后者可以存在孤立节点且计数的是全图graphlet而非特定节点邻域中的graphlet个数

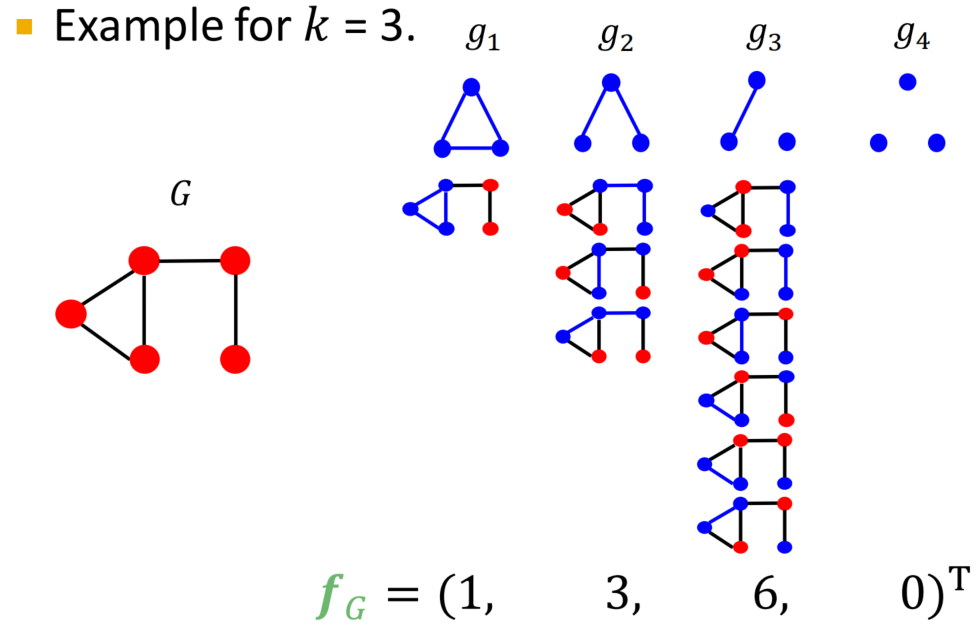
Graphlet Kernel

作用：衡量两个图之间的相似度
特点
Kernel matrix $K=(K(G,G^{\prime }){)}_{G,G^{\prime }}$是半正定的

计算方式：两个图$G$和$G^{\prime }$的graphlet count vector计算数量积

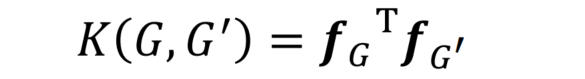
存在的问题：G和G‘的大小不同，数值会存在差距
解决办法：将两个graphlet count vector做归一化处理之后再求数量积

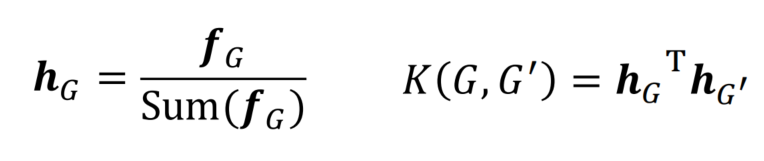
graphlet kernel计算的特点：
在图中寻找子图模式的过程是一个子图匹配问题，寻找所有的子图是一个多项式复杂度的问题$n^k$，但我们还需要进行子图同构检查，这将使得问题变为NP难。因此graphlet kernel的计算实施是很困难的

Weisfeiler-Lehman Kernel

思想：通过不断迭代，使得Bag-of-node degree的范围从one-hop邻域扩大到进行k次，捕捉k-hop neighborhood的信息，作为全图结构信息编码
策略：使用color refinement，得到color count vector
举个例子来观察color refinement的过程






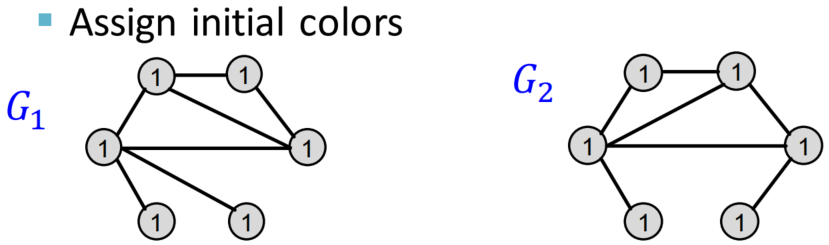
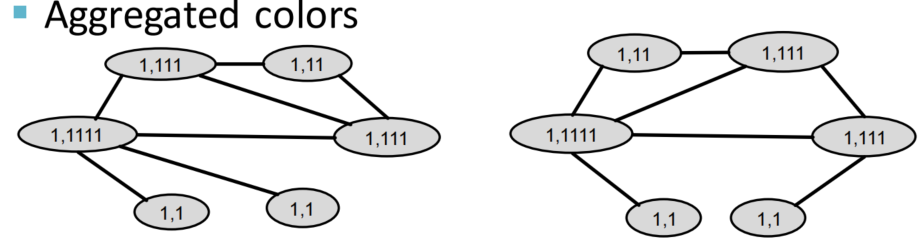
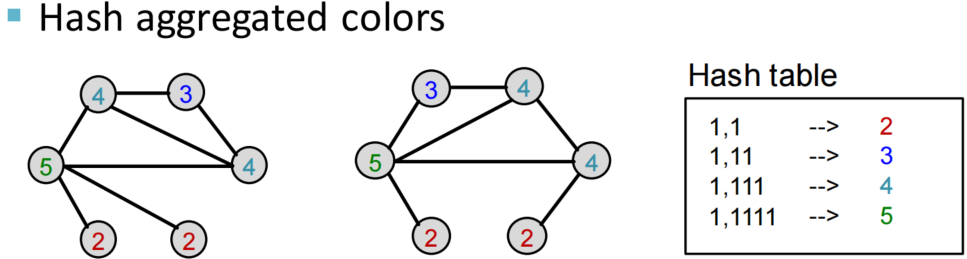
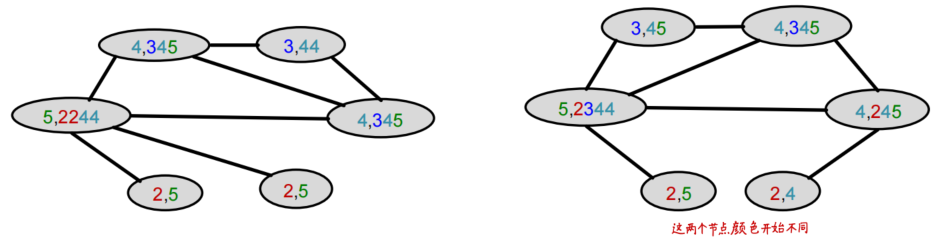
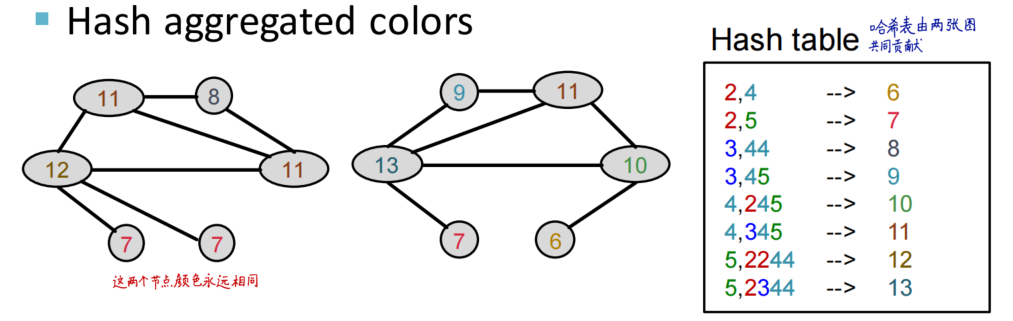
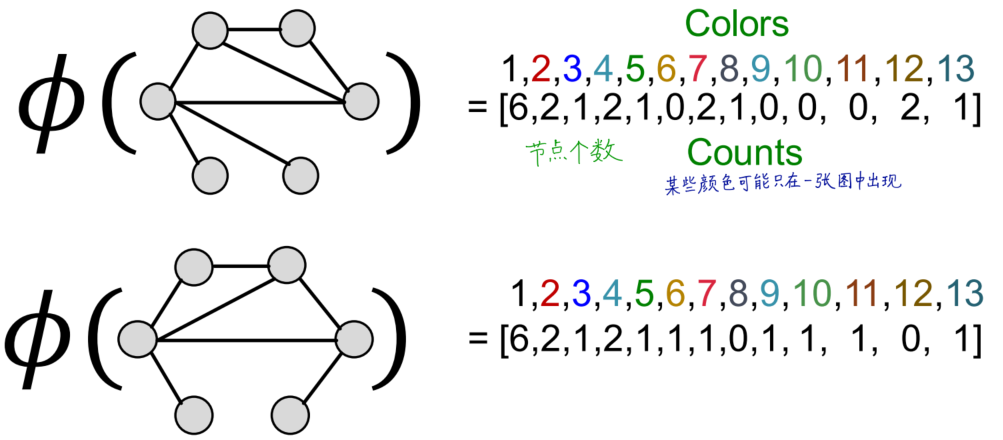
计算WL Kernel：使用G和G’的color count vectors计算内积

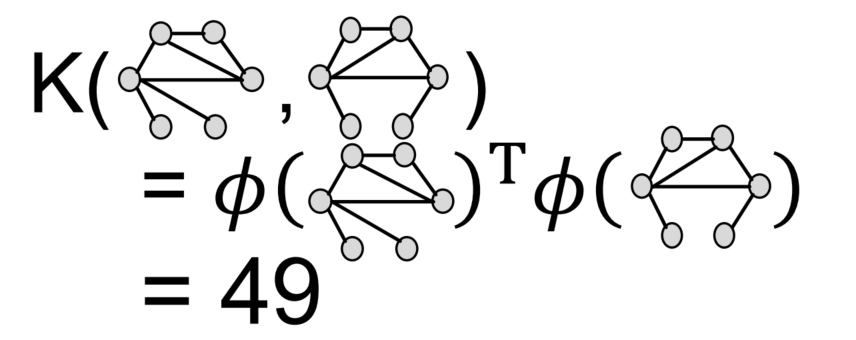
形式化定义color refinement的过程

分析color refinement的计算时间复杂度
获得节点的color表示 即aggregating neighboring colors的过程，其复杂度不超过linear in edges
计算kernel value时，考虑的color数目，也是linear in nodes

参考资料

1. 同济子豪兄课程repo地址：https://github.com/TommyZihao/zihao_course/tree/main/CS224W