- 1头歌平台自建实践项目简易教程_头哥平台
- 2华为OD机试-传递悄悄话(Java&Python&Go)100%通过率_华为od机试传递悄悄话
- 3C++ & QT Creator 开发网络调试助手_网络调试助手源码c++
- 4【STM32】--基于STM32最小系统点亮LED灯
- 5python怎么创建一个文件夹,用python创建一个文件夹_python 创建文件夹
- 6vue+elementUI实现点击左右箭头切换按钮功能_element tabs 添加左右切换按钮
- 7MacOS安装多个Python版本导致Python3: Command not found_python3-config: command not found
- 8算法——马踏棋盘算法(骑士周游问题)/图的深度优先遍历+贪心算法优化
- 9吉林师范计算机考研真题,2021吉林师范大学考研历年真题
- 10C++ 函数调用的压栈过程_函数调用压栈过程 面试
【CS224W】 -- 图机器学习导论
赞
踩
一、图机器学习导论
1. 导论
本讲介绍了图数据挖掘的常见任务、典型方法、应用场景、编程工具。图是描述大自然各种关联现象的通用语言,图无处不在。不同于传统数据分析中样本独立同分布假设,图数据自带了关联结构,需要使用专门的图神经网络进行深度学习。 本讲介绍了斯坦福CS224W公开课的课程大纲;在节点、连接、子图、全图各个层面进行图数据挖掘的典型任务,以及在蛋白质结构预测、生物医药、内容推荐、文献挖掘、社交网络、开源项目评价等领域的应用。


2. 图机器学习研究的问题
图结构和网络结构是非常常见的数据结构,常见的事件图、计算机网络、事务网、社交网络和人际关系等都是图状结构。
图就是用来描述每一个样本之间相互之间有关联的,在此之前描述样本之间都是独立同分布的,而图可以使用节点和边的形式来表述样本之间的关系。
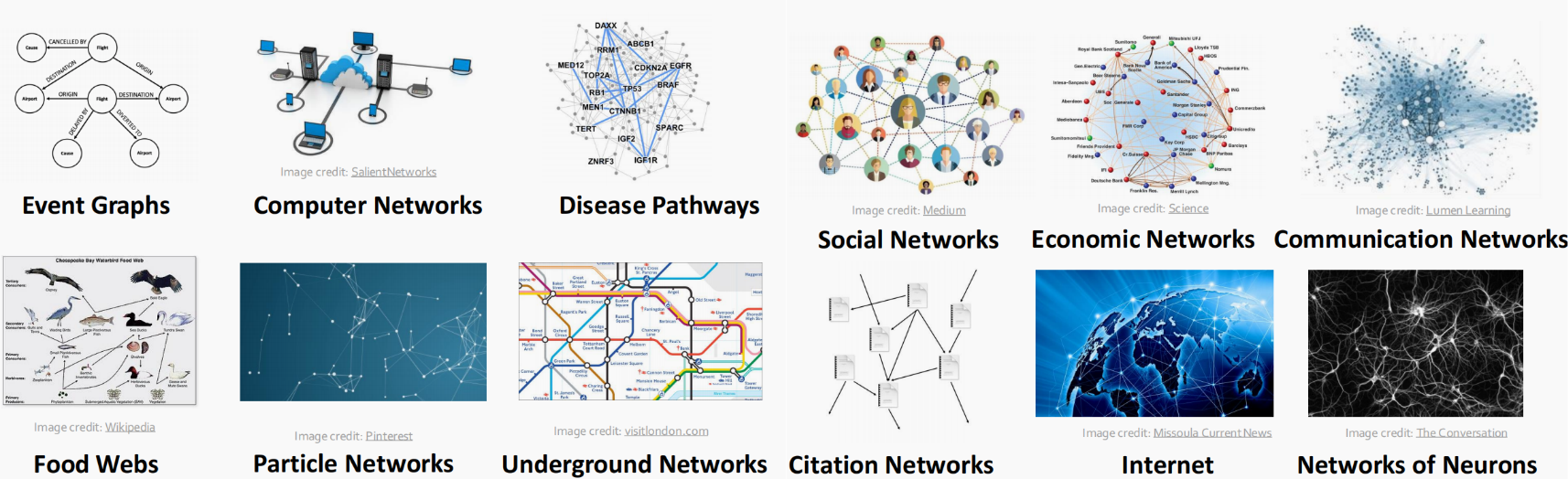
- 无标度网络经常被称为自然图
- 复杂领域具有丰富的关系结构,可以用关系图表示
- 图是对于一些关系的表示,可以表示信息和知识的联系
- 很多时候网络和图的区别十分模糊,通常可以把它们混为一谈
2.1 图学习的难点
- 任意尺寸输入的,如可以往一个模型中输入一个很大的有很多条边的图,也可以输入一个非常小的图
- 没有固定的节点顺序和参考锚点
- 动态变化的数据,如淘宝的顾客信息,编好等都是随时变化的
- 多模态的特征
2.2 图深度学习 vs CV、NLP
- 相比于图像和文本,图结构的大小比较随意且拓扑结构复杂(没有像网格那样的空间局部性)
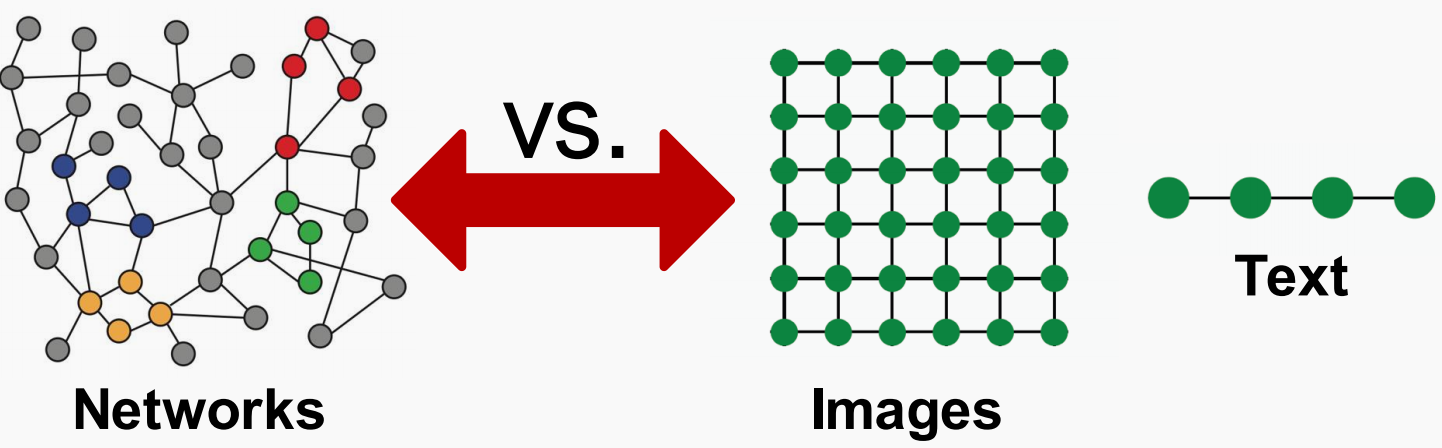
- 没有固定的节点顺序或者参考点
- 通常是动态的,具有多模态特征
2.3 图神经网络结构
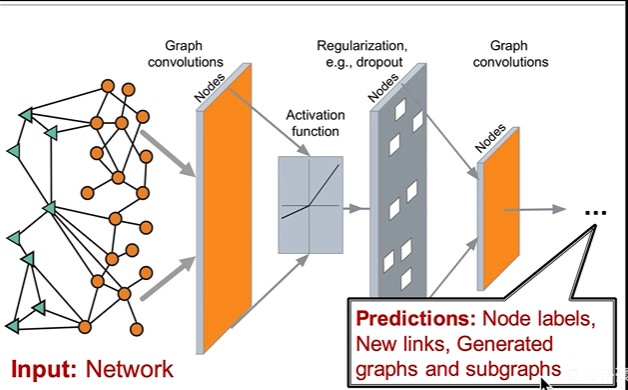
- 输入:一张图
- 通过一连串的图卷积操作和激活函数,这部分也就是黑箱子:实现端到端的学习(表示学习),图神经网络可以自动学习特征,类似卷积神经网络,不需要人工干预教学
- 输出:可能是节点的label标签,也可能是节点之间的连接,也可能是生成另一个图或者另一个子图
2.4 图机器学习的任务
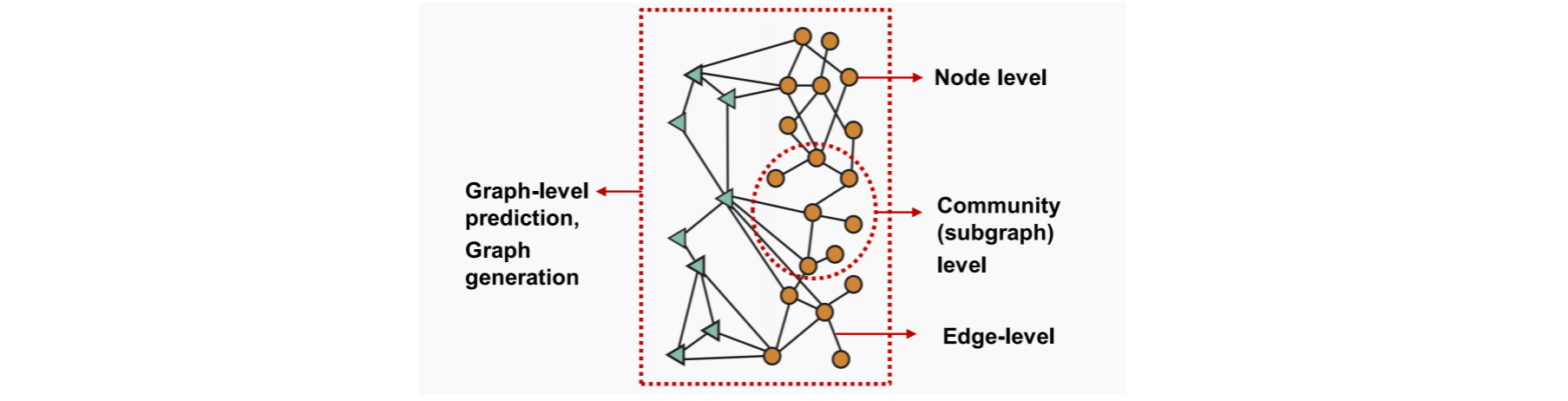
- 图机器学习的四类任务:
- 三类:节点、边、子图分类
- 还有一类:图级别:包括预测任务 graph-level prediction 和 图生成任务 graph generation
2.5 传统的图机器学习任务
- 节点分类:预测节点的属性,如分类在线用户或者商品
- 链接预测:预测两个节点之间是否缺少了链接,如知识图谱补全
- 图分类:如化学中的分子性质预测
- 聚类:检测节点是否构成了一个类别,如社交圈检测
- 图生成:用以药物发现以产生新的分子结构
- 图进化:物理现象的仿真模拟
2.6 图学习应用
- 最短路径的搜索和查找(例如导航)
- 分析节点重要度(度中心性评价,著名的就是PageRank)
- 社群检测(比如银行卡欺诈中,可以通过社群检测判断出哪一片人群经常欺诈)
- 连接预测(在社交网络中很重要,可以推荐你可能认识的人,还有商品的推荐系统也是)
- 节点相似度(也许图中的两个节点距离非常远,但是他们有非常大的相似性,我们就可以通过节点相似度找到他们)
- 图嵌入(把一个节点映射为一个d维向量,例如Node2Vec。这个d维的向量就可以反应节点的语义和连接关系)
3. 图的基本表示
- 图的本体设计
- 图的种类(有向、无向、异质、二分、连接带权重)
- 节点连接数
- 图的基本表示 - 邻接矩阵
- 图的基本表示 - 连接列表和邻接列表
- 图的连通性
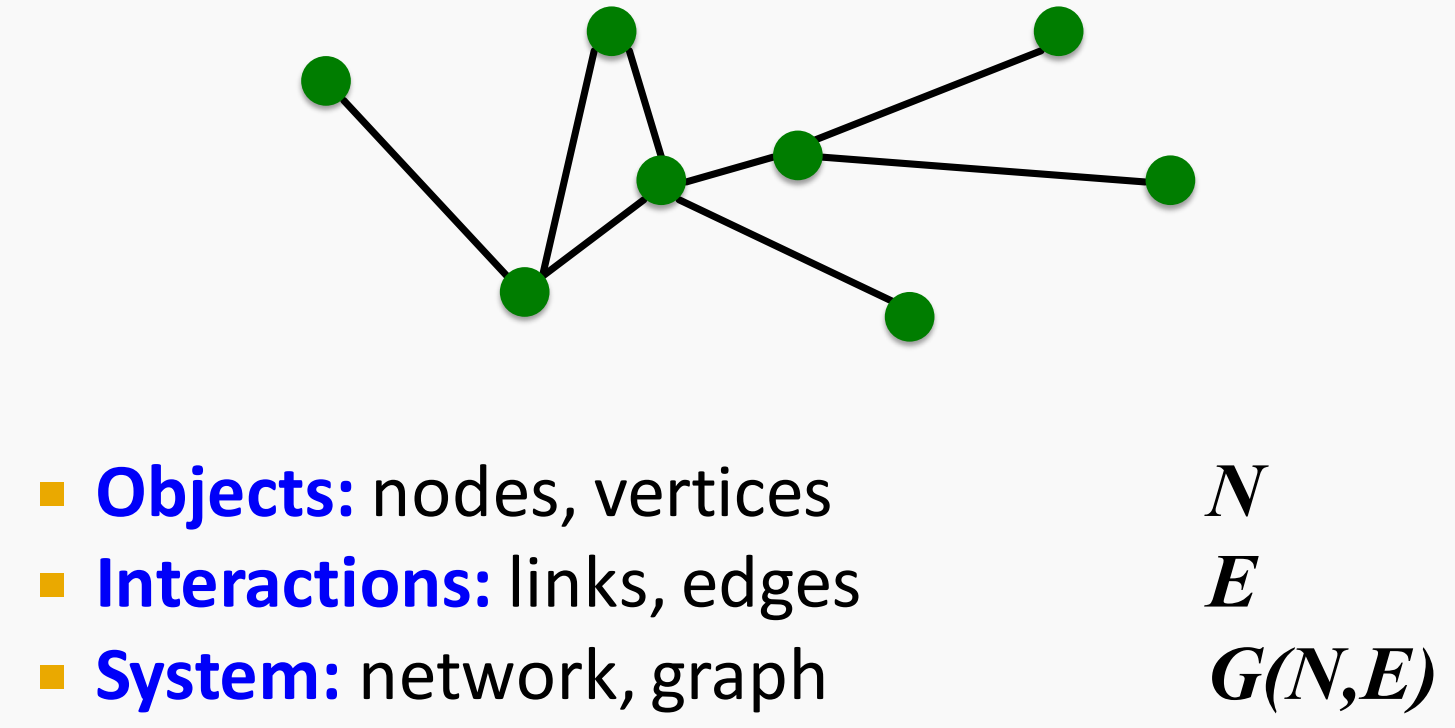
常见的表示方式使用节点集合N和边集合E构成一个图结构 G ( N , E ) G(N, E) G(N,E)
3.1 本体图
图中哪些作为节点,哪些作为边就是本体图考虑的问题
如下图所示就是一个本体图,通常我们在开始做图学习的任务之前,在导入数据之前,我们就应先构建出本体图,在具体导入数据的时候只不过是在本体图对应的节点中填入实际的数值而已
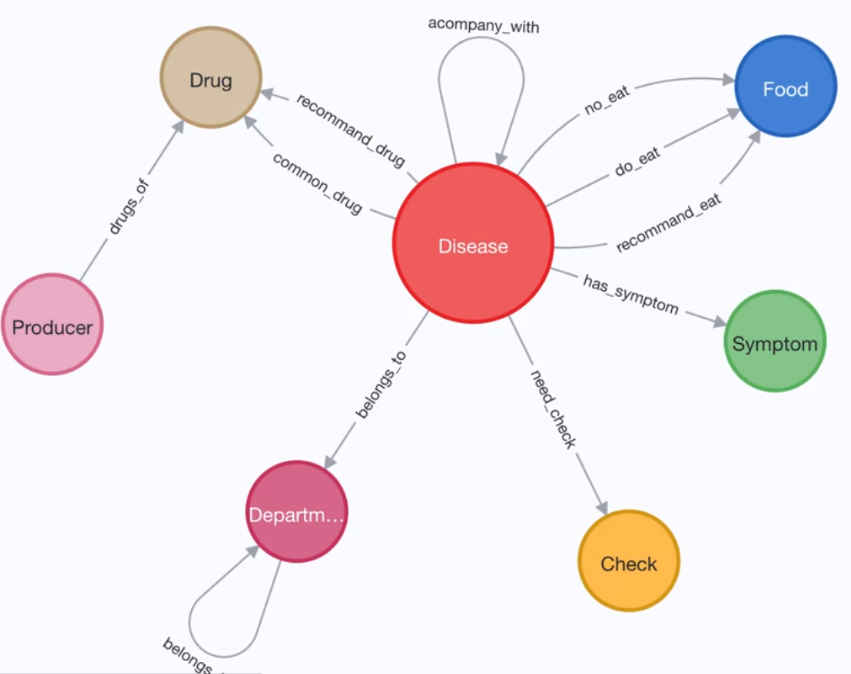
本体图的设计取决于将来想解决什么问题,而且本体图可以是唯一的,可以是不唯一的
3.2 图的种类
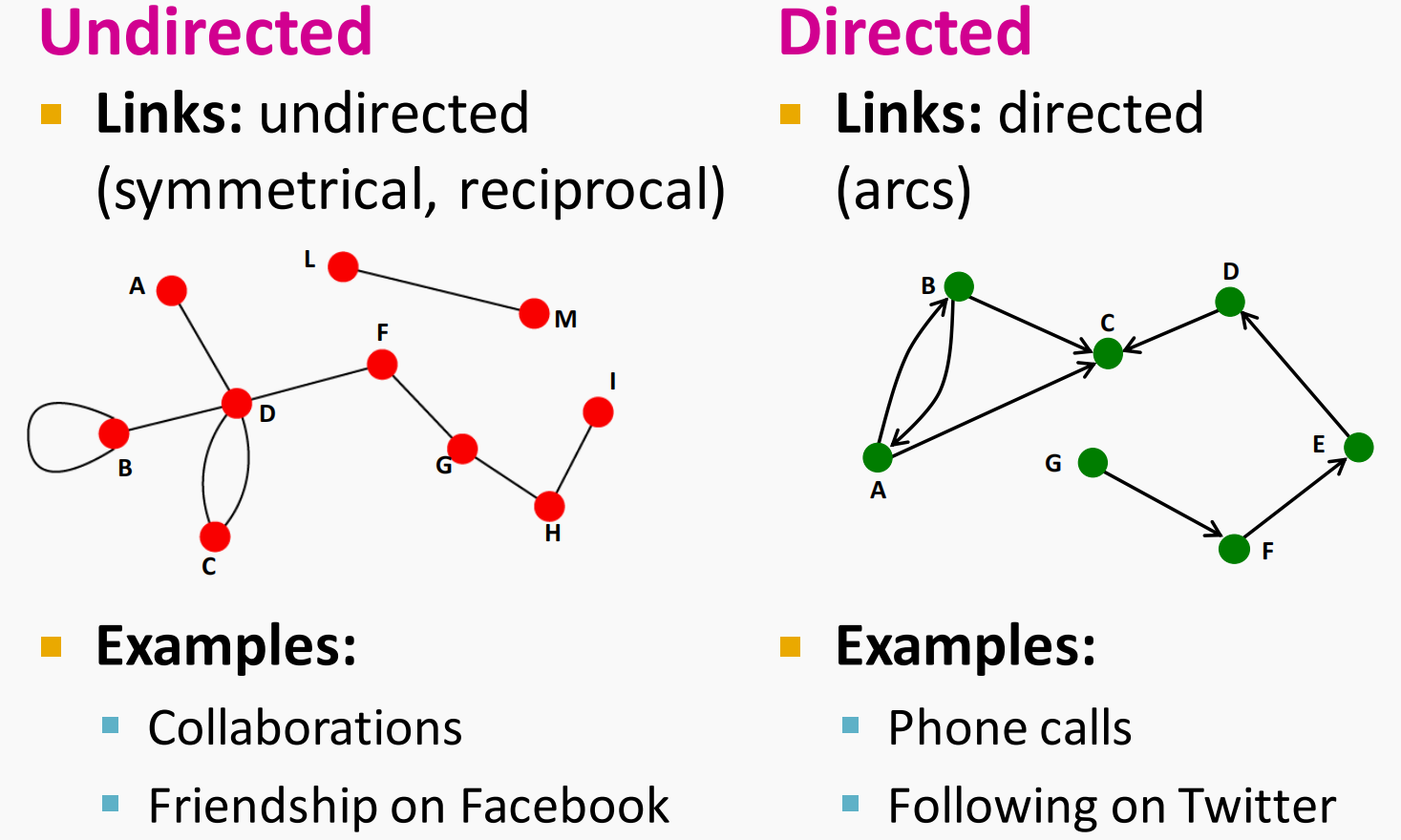
- 有向图和无向图
区别就在于边是否具有方向性,节点的度(node degree)表示包含这个节点的边的数量,而在有向图中又可以具体分为出度和入度。
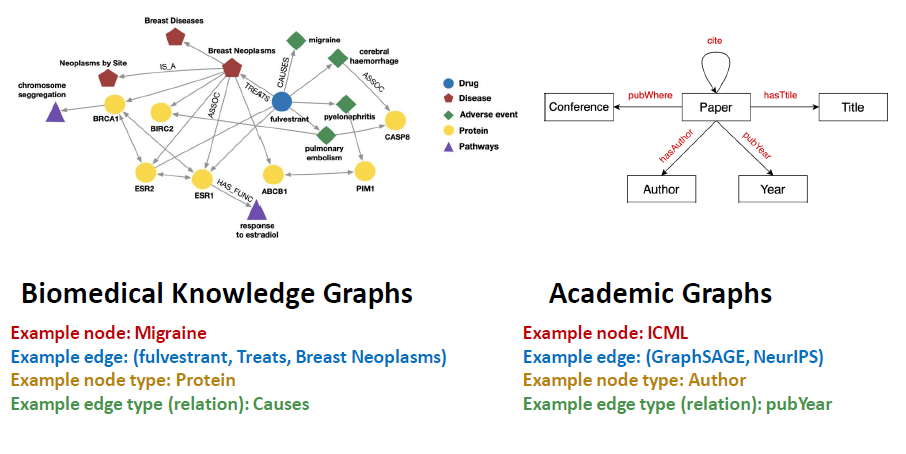
- 异质图

图中的节点或者连接会有不同的类型
很多图都是异质图,例如:
- 二分图
一种特殊的图结构,可以将图中的节点分成两个不相交的集合U和V,使得图中的任意一条边的两个顶点分别属于U和V,如
- 作者和文章
- 演员和电影
- 菜肴和原材料
- 用户和商品

- 无权图和有权图
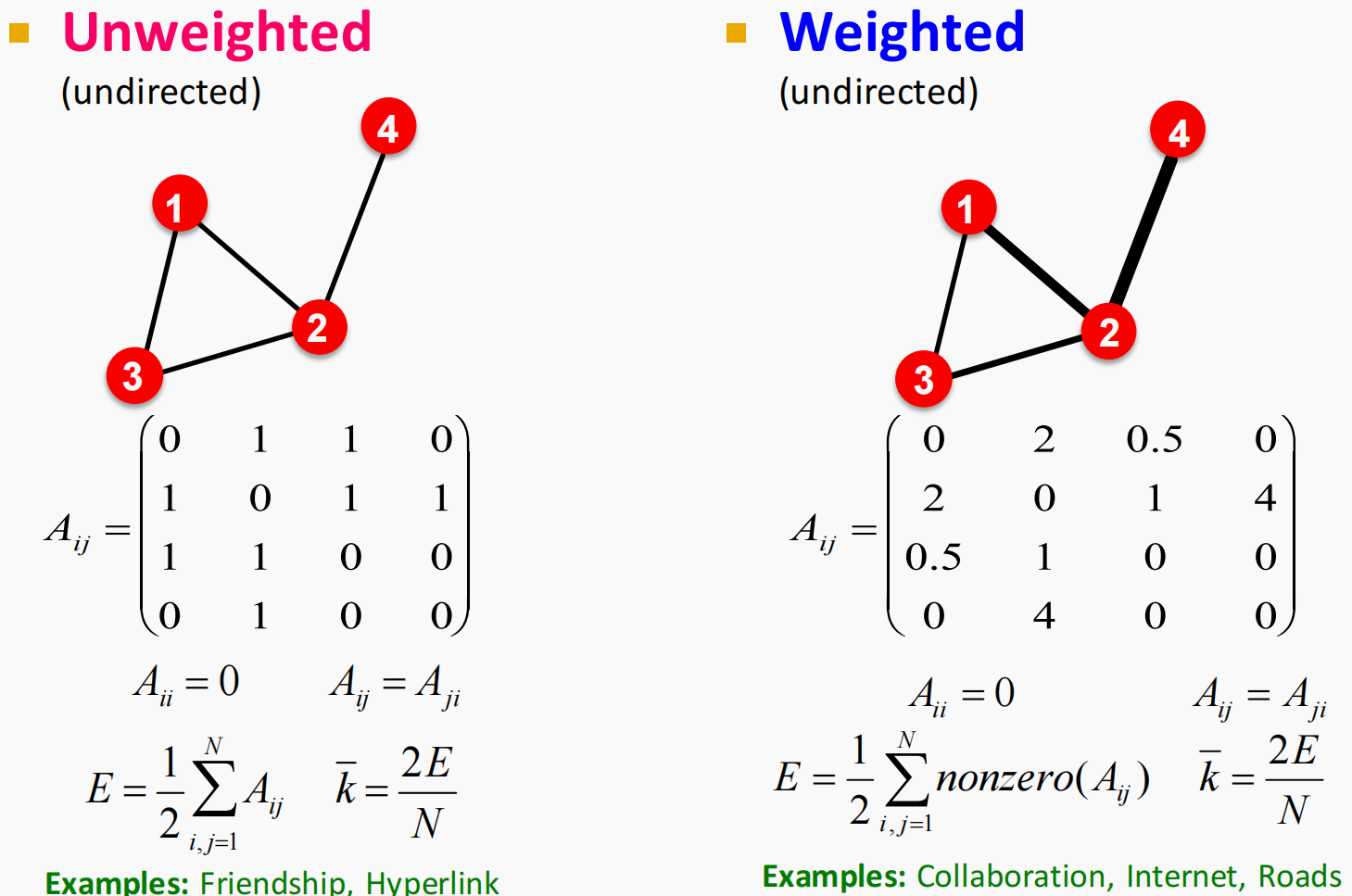
- 自循环、多边图
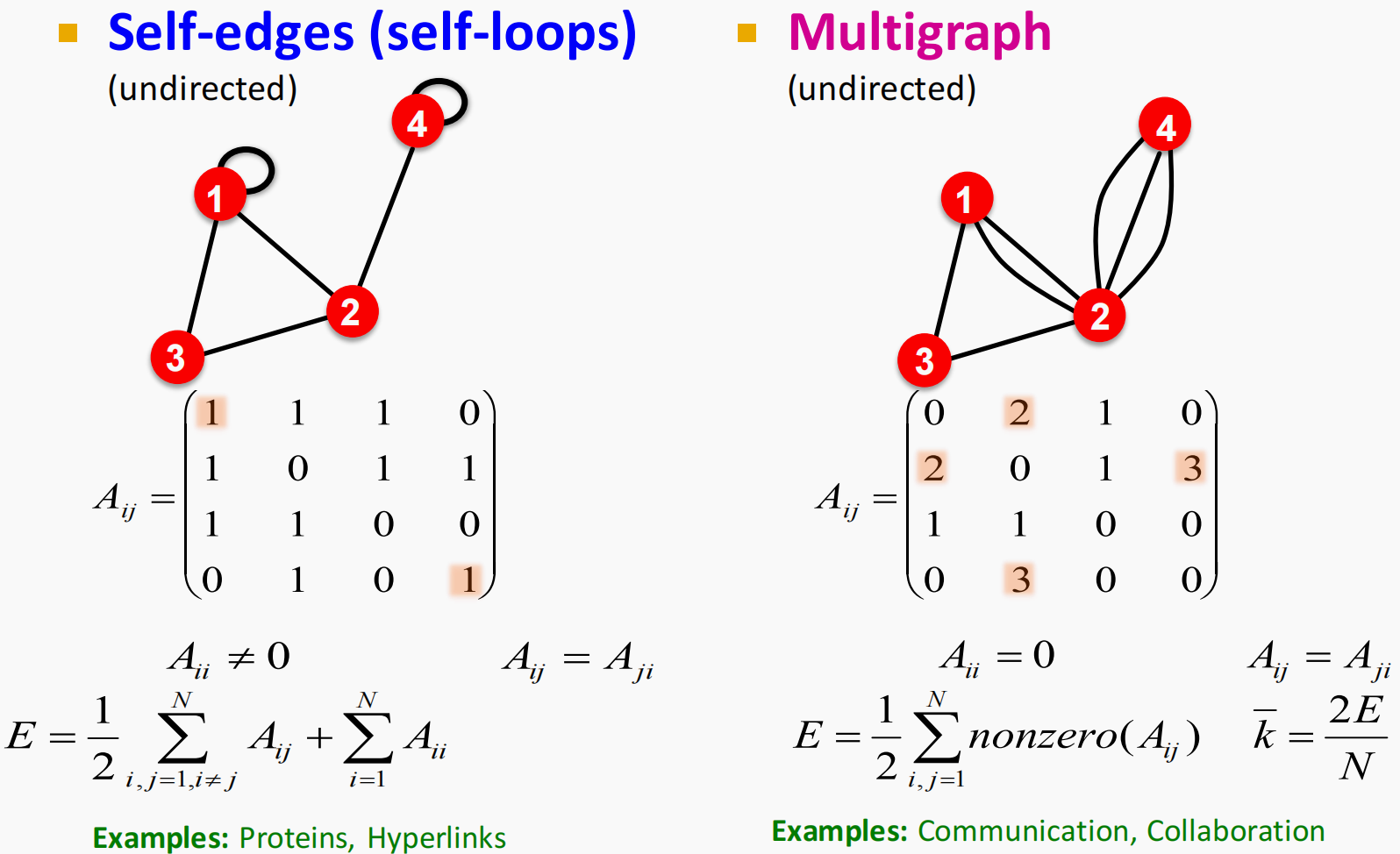
- 同构图和异构图
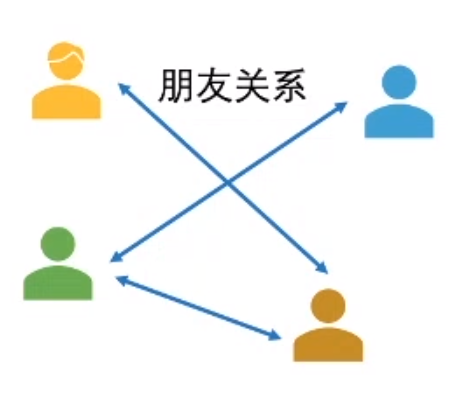
同构图中,节点的种类和连接关系都只有一种。比如:人际关系网络
- 两个图G和H是同构图(isomorphic graphs),能够通过重新标记图G的顶点而产生图H。
- 如果G和H同构,那么它们的阶是相同的,它们大小是相同的,它们个顶点的度数也对应相同。
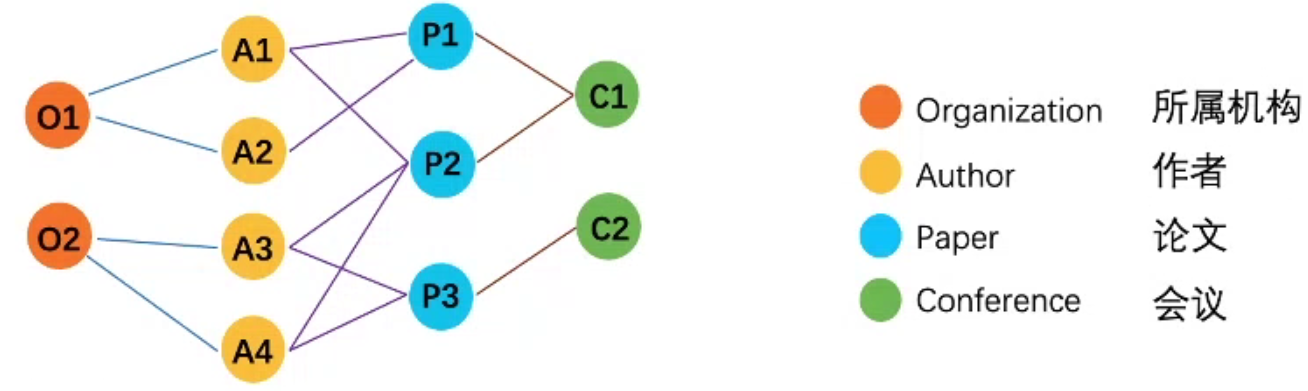
异构图,是一个与同构图相对应的新概念,节点的种类和连接关系有多种类型。比如:学术网络
3.3 节点的度
无向图:
- 节点连接数:一个节点存在多少个连接(度)
- 平均连接数:一个节点的平均连接数(2E/N)
有向图:
- 入度、出度
- 一个节点的入度=0,则为起始节点
- 一个节点的出度=0,则为终止节点
- 平均连接数:E/N节点和边一一对应
- 平均入度连接数 = 平均出度连接数
节点连接数可以用来表示节点的重要性(中心度/枢纽度)
3.4 图的基本表示
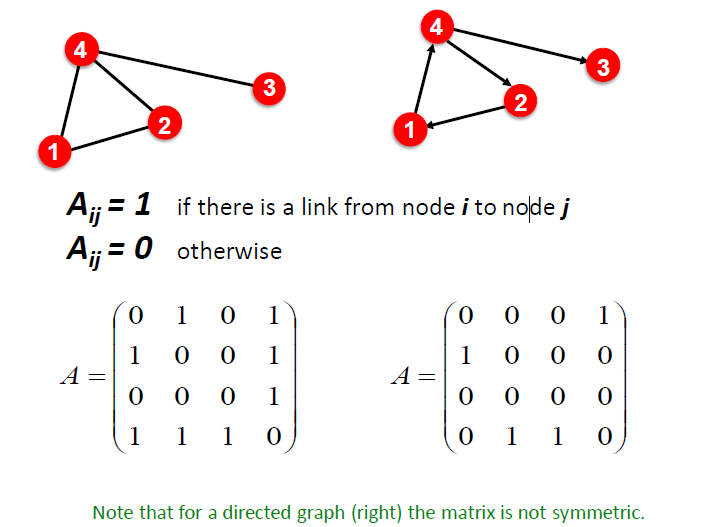
(1)邻接矩阵
无向图:
- 对称矩阵,关于主对角线对称
- 主对角线表示自己指向自己的边,若没有则为0
- 连接总数:看矩阵一半即可(所有非零元素求和 / 2),既可以按行计算,也可以按列计算
有向图:
- 非对称阵
- 入度按行求和
- 出度按列求和
- 连接总数:矩阵中所有非零元素求和
稀疏矩阵:
- 常见的矩阵都是稀疏矩阵(矩阵中零的节点远远多于非零节点)
(2)连接列表和邻接列表
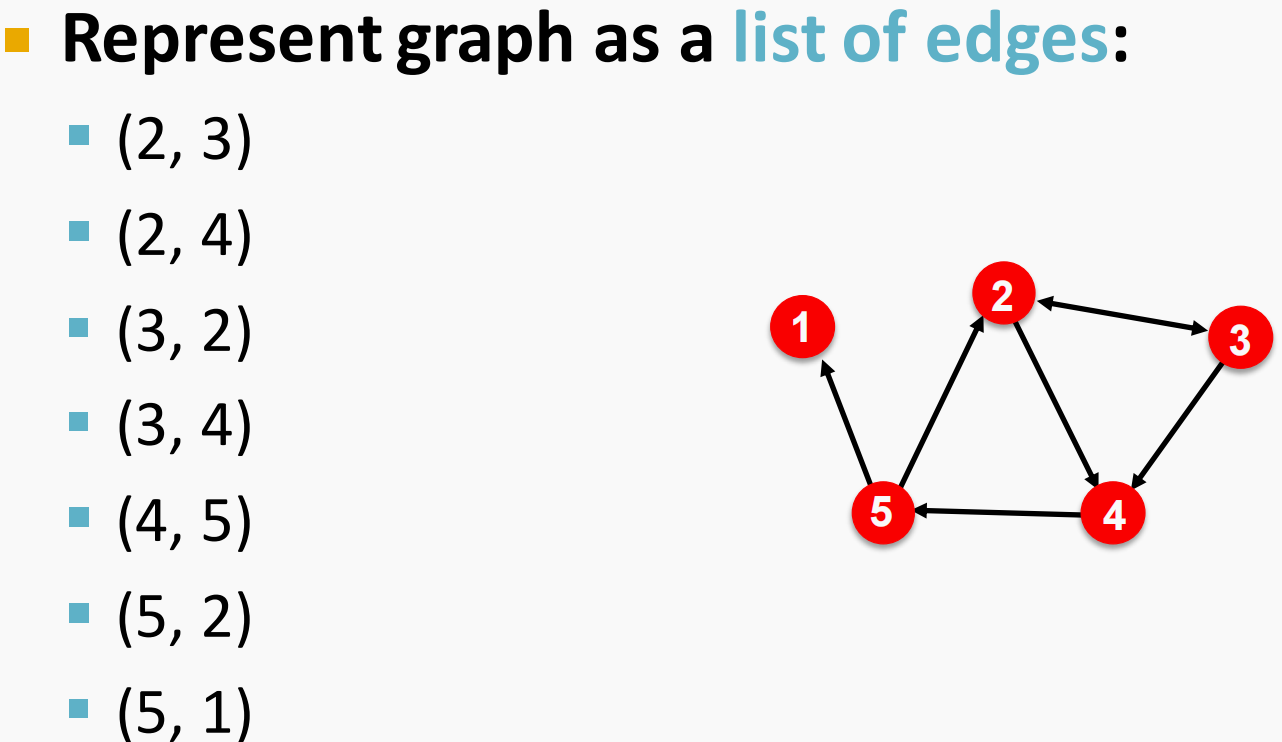
连接列表:
- 只记录存在连接的节点对
- 节省存储空间
- 连接表(三元组:起始节点;终止节点;关系)
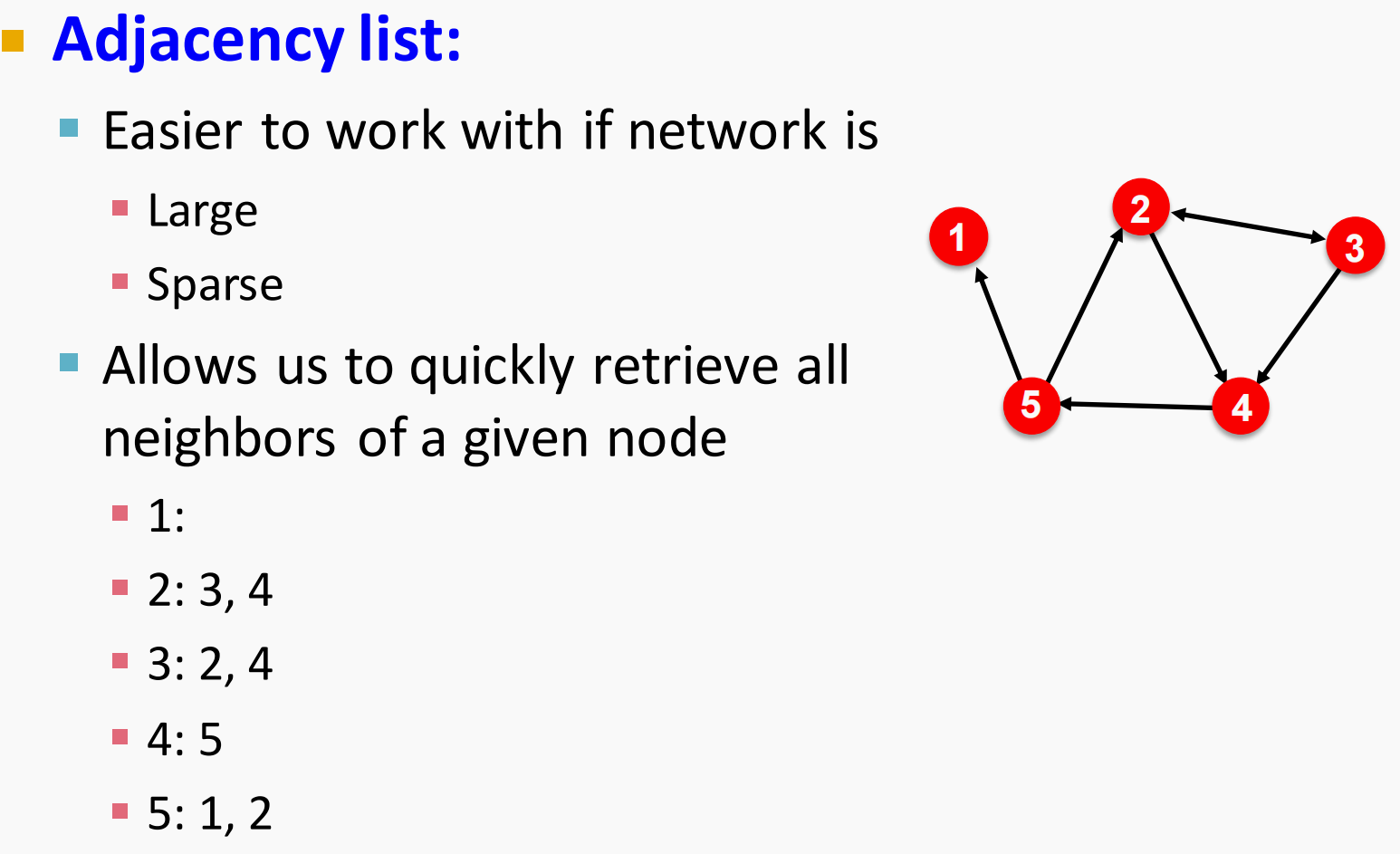
邻接列表:
- 将所有和某个节点相关的(指向)的节点按照行记录下来
- 按行存放
- 进一步压缩存储空间,同时没有丢失信息
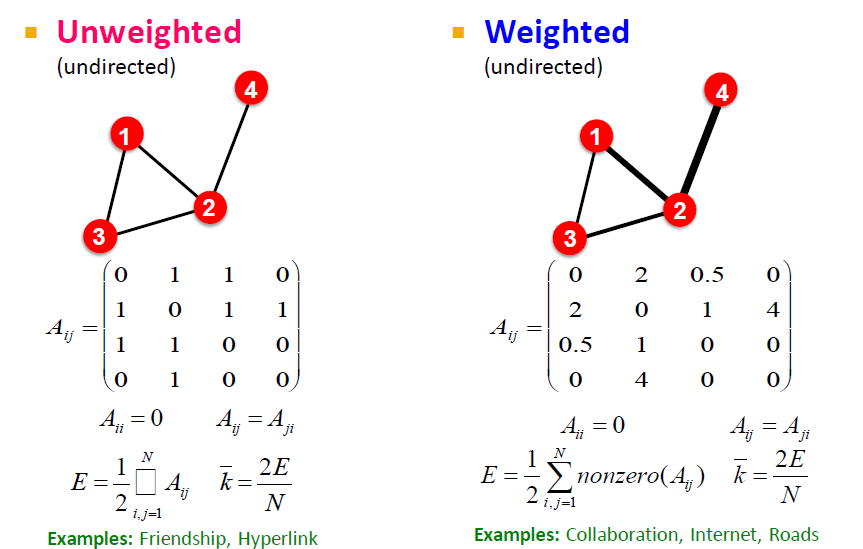
(3)带权图和不带权图
不带权图:
- 邻接矩阵中的节点非1即0
带权图:
- 邻接矩阵中的节点不是非1即0,带有权值
不管是带权图还是不带权图,无向图计算连接总数都是1/2矩阵中非零节点求和,平均连接总数都是2E / N
3.5 图的连通性
(1)连通图
- 图中的任意两个顶点都能找到边到达,就是连通图
- 如果几个不连通图中出现了能够将他们连接起来的桥接节点,那么就会打破不连通图邻接矩阵分块对角的形式
(2)不连通图
- 如果图中存在任意两个顶点不能找到边到达,则不是连通图
- 其中最大的连通部分称作最大连通子图
- 数据分布呈现分块对角的形式
(3)强连通图
- 对于有向图而言,如果任意两个节点都能找到边到达,那么这个图就是强连通图
(4)弱连通图
- 对于有向图而言,如果存在两个节点不能找到边到达,那么这个图就是弱连通图
- 但是其中的一些子图也许是强连通的,称为强连通域(
SCC) - 从
SCC中指出来的节点称为Out-component - 指向
SCC的节点称为In-component - 对于一张图的SCC分解是非常重要的
编程工具
学习资料
https://github.com/lyc686/CS224W_notes/
https://github.com/shenhao-stu/CS224W-Fall2021
https://andyguo.blog.csdn.net/article/details/128908145


