动态规划从入门到精通 最长公共子串、最长公共子序列问题

目录

辨析串和序列

辨析子串和子序列

最长公共子串问题

 公式解说：

公式的伪代码：

 需要注意的是：

最长公共子序列问题

公式解说：

伪代码如下：

需要注意的是： 

 手搓代码巩固一下：

最长公共子串   acwing 508 上海交通大学考研机试题

输入格式

输出格式

数据范围

输入样例：

输出样例：

代码

 最长公共子序列 acwing 3510 上海交通大学考研机试题

输入格式

输出格式

数据范围

输入样例1：

输出样例1：

输入样例2：

输出样例2：

 代码

辨析串和序列

       在计算机科学和算法设计中，“串”（string）和"序列"（sequence）是两个常用的概念，它们可以用于表示一组元素的集合。

1. 串（String）：串是由字符组成的有限序列，字符可以是字母、数字、符号等。在计算机中，字符串常用于表示文本或数据。串的特点是元素有序且可重复（即允许出现重复的字符）。

   例如，“hello”、“abc123”、"foo bar"都是字符串。

2. 序列（Sequence）：序列是指一系列元素按照一定顺序排列组成的集合。序列的元素可以是任意类型的，不仅限于字符。

   序列有两种常见的类型：线性序列和非线性序列。

   • 线性序列：元素按照线性的顺序排列，可以用一维数组或链表表示。例如，数组 [1, 2, 3, 4] 和链表 (1, 2, 3, 4) 都是线性序列。
   • 非线性序列：元素之间存在非线性的关系，常用于表示树、图等数据结构中的元素关系。例如，二叉树的遍历序列就是一种非线性序列。

        串是序列的一种特殊形式，是由字符组成的有限序列。而序列是一个更广泛的概念，可以包含任意类型的元素，并有不同的表示方式，比如线性序列和非线性序列。

以上是一些晦涩难懂的定义，大概了解其意思就足够了，重点在下面：

辨析子串和子序列

       在计算机科学中，“子串”（substring）和"子序列"（subsequence）是两个常用的概念，它们都可以用于描述一个字符串或序列的一部分。

1. 子串（substring）：子串是原字符串中由相邻字符组成的一段连续子序列，它可以是原字符串中的任意一段连续区间。

   例如，在字符串"example"中，“exa”、“mpl”、"le"等都是该字符串的子串。

2. 子序列（subsequence）：子序列是原序列中从左到右不一定相邻的元素组成的子序列，元素的顺序与原序列相同。

   例如，在序列 [1, 3, 5, 2, 4] 中，[1, 5, 4]、[3, 5, 2, 4]、[1, 3, 2] 等都是该序列的子序列。

       子串和子序列都是原字符串或序列的一部分，它们的区别在于子串是相邻的字符组成的一段连续子序列，而子序列是从原序列中取出若干个元素组成的子序列，不一定是相邻的。

最长公共子串问题

       在动态规划中，你要将某个指标最大化。在这次学习中，你要找出两个单词的最长公共子串，hish和fish的公共子串是什么呢？最长公共子串的长度是多少呢？

      解决动态规划问题要擅于利用网格，单元格中的值就是你要优化的值。

      如何将这个问题划分为子问题呢？需要比较子串：不是比较hish和fish,先比较hi和fi，再比较his和fis（思想而已）。每个单元格都将包含这两个子串的最长公共子串的长度。这也给你提供了线索，让你觉得坐标轴就是这两个单词。因此，网格类似于下面：

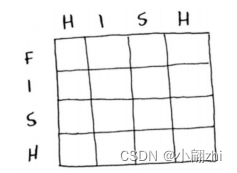
 请尝试为这个问题找到计算单元格值的公式。给你一点提示：下面是这个单元格的一部分。

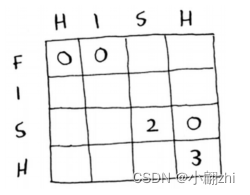
其他单元格的值呢？别忘了，每个单元格都是一个子问题的值。为何单元格（3,3）的值为2呢？又为何单元格（3,4）的值为0呢？

揭晓答案

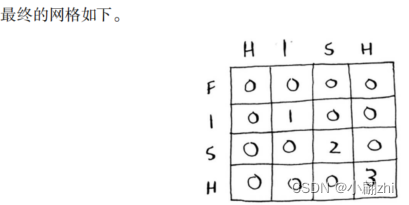
我们使用下面的公式来计算每个单元格的

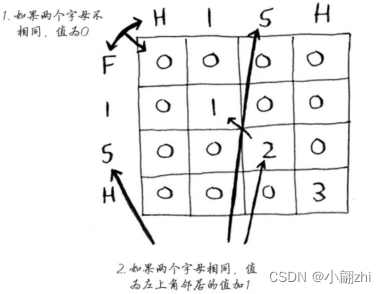
 公式解说：

如果两个字母不相同，值为0；如果两个字母相同，值为左上角的值加1

公式的伪代码：

if a[i]==b[j]://两个字母相同
   c[i][j] = c[i-1][j-1]+1
else//；两个字母不同
    c[i][j]=0

 查找单词hish和vista的最长公共子串时，网格如下：

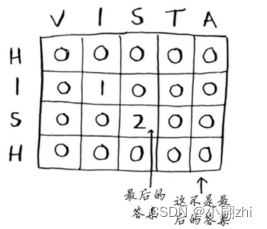
 需要注意的是：

最长公共子串的问题的最终答案并不是在最后一个单元格中，答案为网格中最大的数字——他可能并不位于最后的单元格中。

最长公共子序列问题

fish和fosh的最长公共子序列长度是多少呢，fort和fosh的最长公共子序列长度是多少呢？

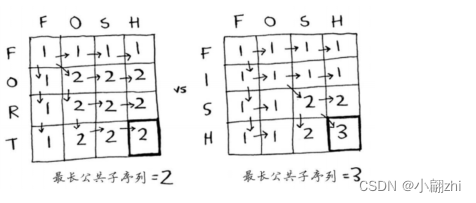
下面是填写各个单元格时使用的公式

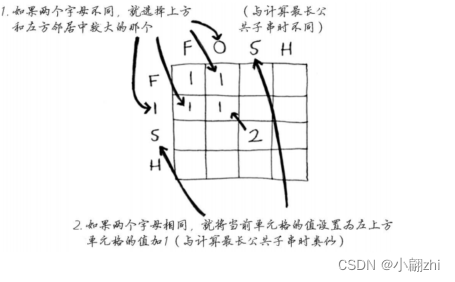
公式解说：

如果两个字母不同，就选择上方和左方中较大的那个，如果两个字母相同，就等于左上方单元格的值加1

伪代码如下：

if a[i]==b[j]://两个字母相同
    c[i][j]=c[i-1][j-1]+1
else://两个字母不同
    c[i][j]=max(c[i-1][j],c[i][j-1])

需要注意的是： 

这个问题的最终答案是在最后一个单元格中

 手搓代码巩固一下：

最长公共子串   acwing 508 上海交通大学考研机试题

给定两个字符串，求这两个字符串的不包含数字的最长公共子串的长度。

输入格式

共两行，每行一个由小写字母和数字构成的字符串。

输出格式

一个整数，表示给定两个字符串的不包含数字的最长公共子串的长度。

如果不存在满足要求的非空公共子串，则输出 0。

数据范围

输入字符串的长度均不超过 10000。

输入样例：

ab123abccff
abcfacb123

输出样例：

3

代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e4+10;
char a[N],b[N];
int c[N][N];
int main()
{
    cin>>a>>b;
    int i,j,Max = 0;
    for(i=0;i<strlen(a);i++)
    {
    	for(j=0;j<strlen(b);j++)
    	{
    		if((a[i]==b[j]) && a[i]>=97&&a[i]<=122 )
    		{
    			if(i==0||j==0)//解决当i或j为0时，i-1 j-1使数组下标越界
    			c[i][j]=1;
    			else
			   c[i][j]=c[i-1][j-1]+1;
			}
    		else
    		c[i][j]=0;
    		Max = max(Max,c[i][j]);
		}
	}
	cout<<Max;
	return 0;
 } 

 最长公共子序列 acwing 3510 上海交通大学考研机试题

给出两个长度为 n 的整数序列，求它们的最长公共子序列（LCS）的长度，保证第一个序列中所有元素都不重复。

注意：

• 第一个序列中的所有元素均不重复。
• 第二个序列中可能有重复元素。
• 一个序列中的某些元素可能不在另一个序列中出现。

输入格式

第一行包含一个整数 n。

接下来两行，每行包含 n个整数，表示一个整数序列。

输出格式

输出一个整数，表示最长公共子序列的长度。

数据范围

1≤n≤10的6次方,
序列内元素取值范围 [1,10的6次方]。

输入样例1：

5
1 2 3 4 5
1 2 3 4 5

输出样例1：

5

输入样例2：

5
1 2 3 5 4
1 2 3 4 5

输出样例2：

4

 代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<math.h>
using namespace std;
const int N = 1e3+10;
int a[N],b[N];
int c[N][N]; 
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	for(int i=1;i<=n;i++)
	cin>>b[i];
	int i,j;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=n;j++)
		{
			if(a[i]==b[j])
			c[i][j] = c[i-1][j-1]+1;
			else
			c[i][j] = max(c[i][j-1],c[i-1][j]);
		}
	}
	cout<<c[n][n];
	return 0;
}

提示：这两题手搓只是学习这个知识点，都会超时

       在动态规划中，一个重要的问题是如何设计状态转移方程，将原问题划分为子问题并与之建立递推关系，一般采用数学归纳法的思路，从较小的子问题开始递推，逐步推导出大问题的解。